Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПОДОБНЫЕ ТРЕУГОЛЬНИКИ
Содержание
- 1. ПОДОБНЫЕ ТРЕУГОЛЬНИКИ
- 2. ПЛАНПропорциональные отрезки.Свойство биссектрисы треугольника.Определение подобных треугольников.Отношение периметров подобных фигур.Отношение площадей подобных фигур.Признаки подобия треугольников.
- 3. Пропорциональные отрезкиОтношением отрезков называется отношение их длин.Отрезки
- 4. ПРИМЕРДаны два прямоугольных треугольникаСтороны ΒC и CA
- 5. Пропорциональность отрезковПонятие пропорциональности вводится для любого числа отрезков.например
- 6. Подобные фигурыПредметы одинаковой формы, но разных размеровФотографии,
- 7. Подобные фигурыВ геометрии фигуры одинаковой формы называют
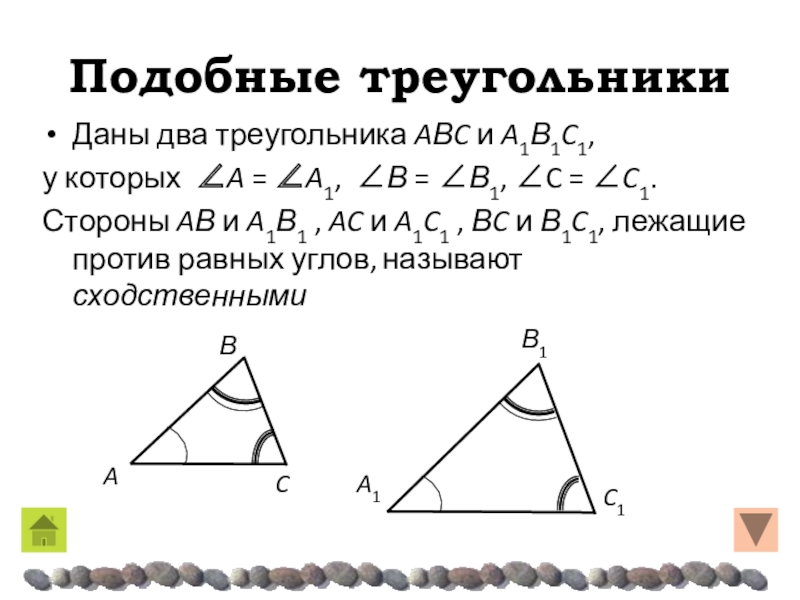
- 8. Подобные треугольникиДаны два треугольника AΒC и A1Β1C1,у
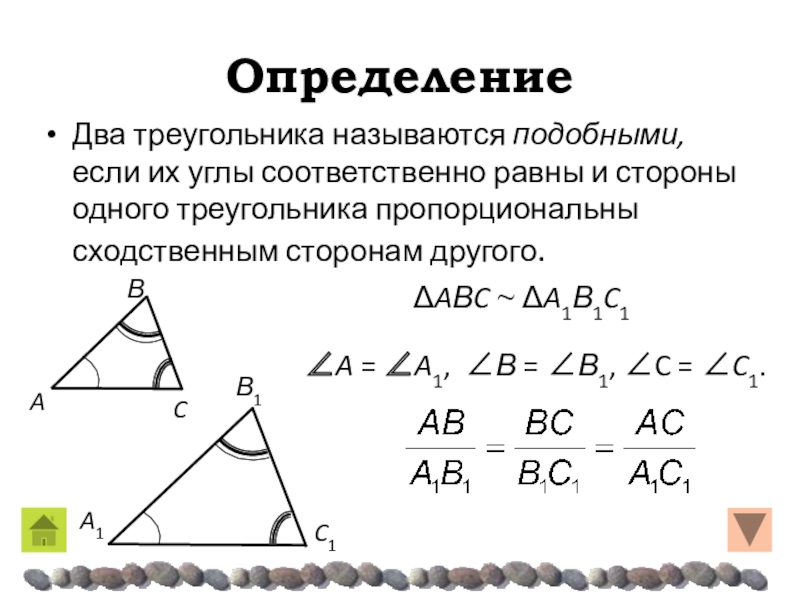
- 9. ОпределениеДва треугольника называются подобными, если их углы
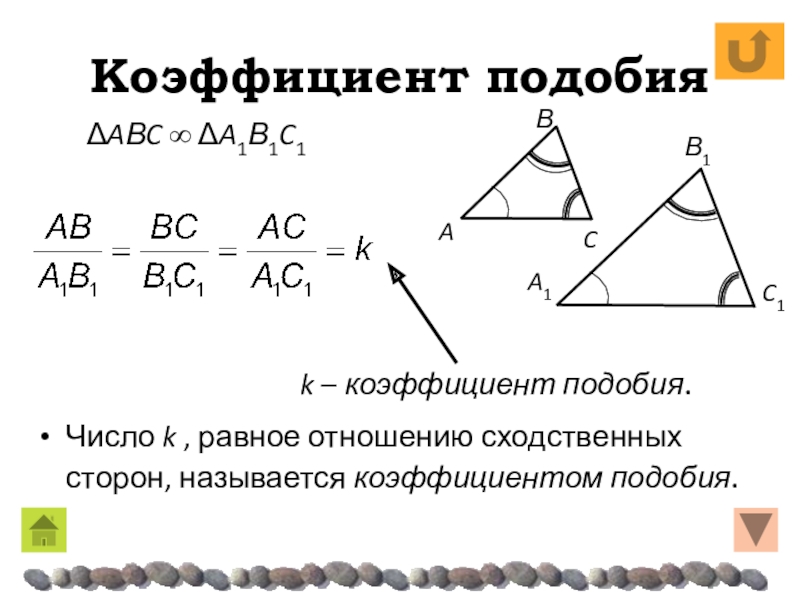
- 10. Коэффициент подобияЧисло k , равное отношению сходственных сторон, называется коэффициентом подобия.ΔAΒC ∞ ΔA1Β1C1k – коэффициент подобия.
- 11. Дополнительные свойстваОтношение высот подобных треугольников, проведенных к
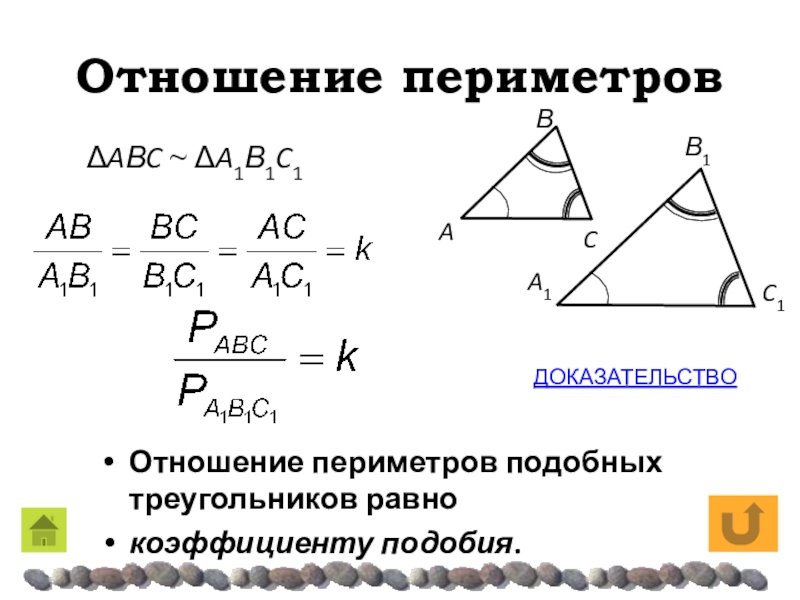
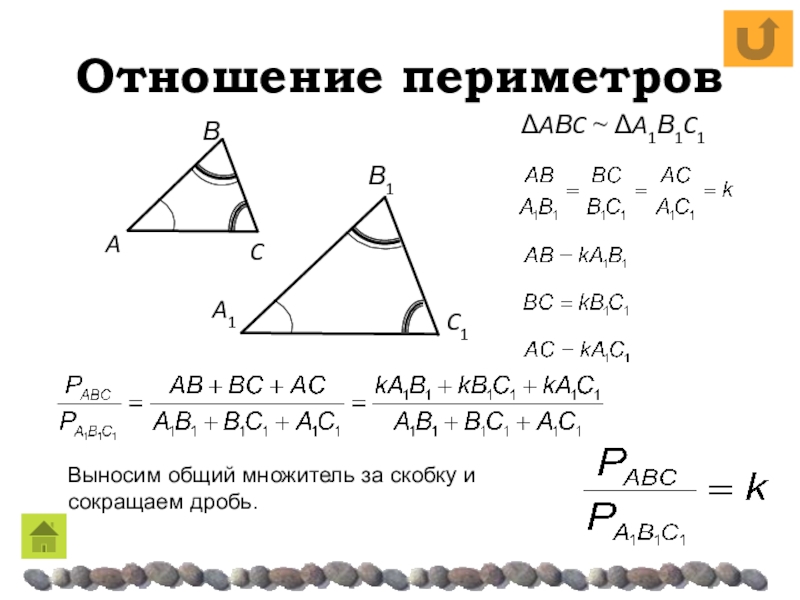
- 12. Отношение периметровОтношение периметров подобных треугольников равно коэффициенту подобия.ΔAΒC ~ ΔA1Β1C1ДОКАЗАТЕЛЬСТВО
- 13. Отношение периметровВыносим общий множитель за скобку и сокращаем дробь.
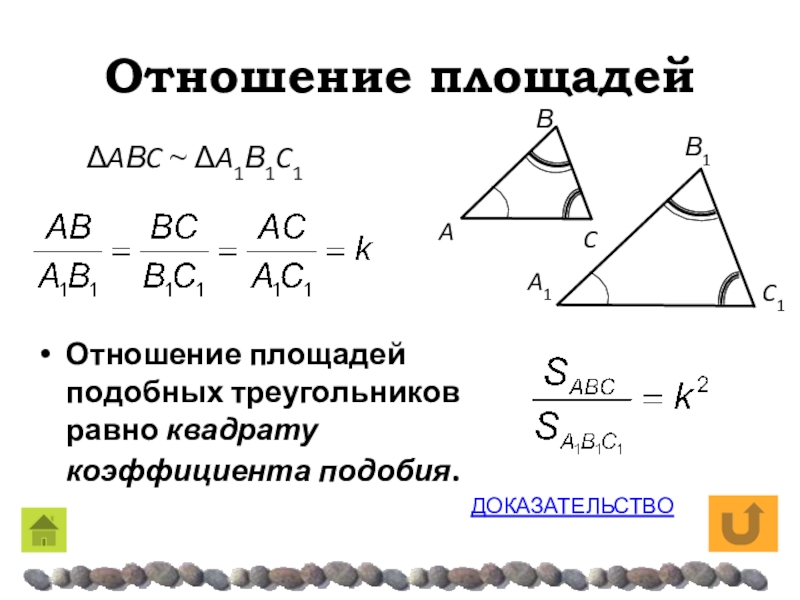
- 14. Отношение площадейОтношение площадей подобных треугольников равно квадрату коэффициента подобия.ΔAΒC ~ ΔA1Β1C1ДОКАЗАТЕЛЬСТВО
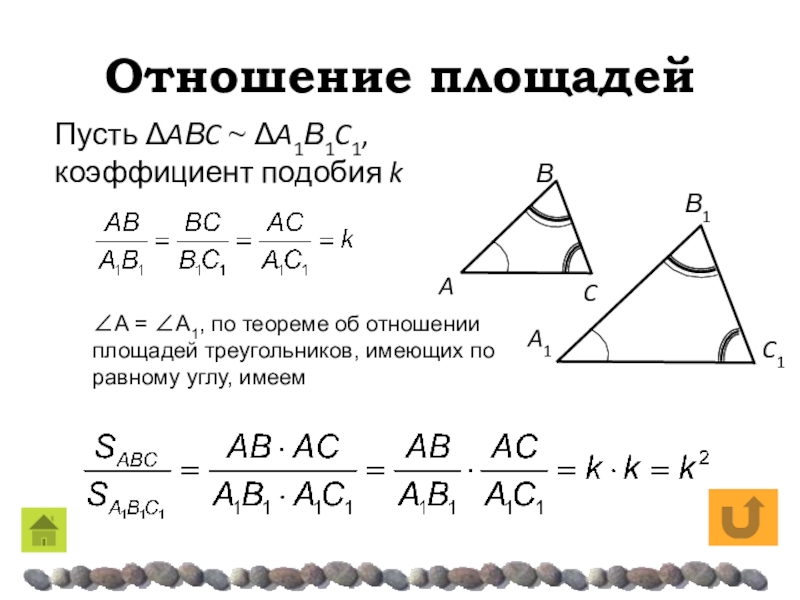
- 15. Отношение площадейПусть ΔAΒC ~ ΔA1Β1C1, коэффициент подобия
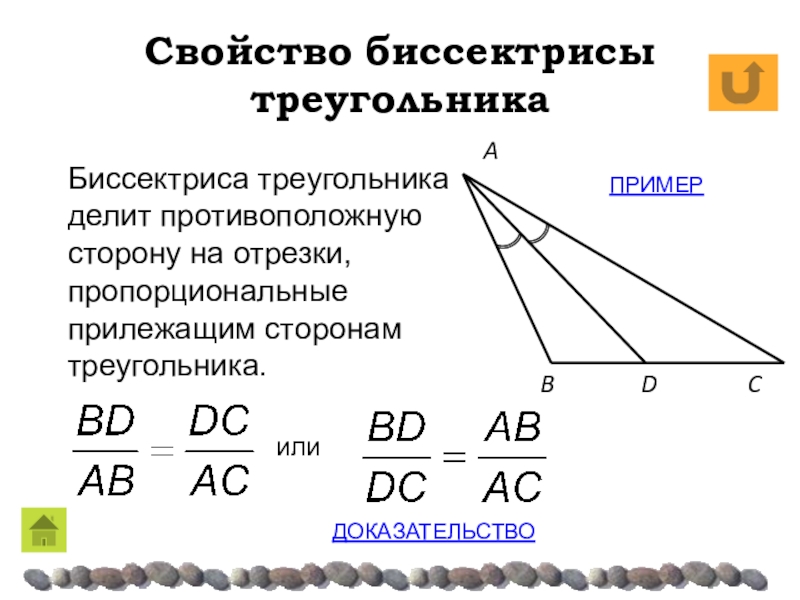
- 16. Свойство биссектрисы треугольникаC BAБиссектриса треугольника делит противоположную сторону на отрезки, пропорциональные прилежащим сторонам треугольника.DилиДОКАЗАТЕЛЬСТВОПРИМЕР
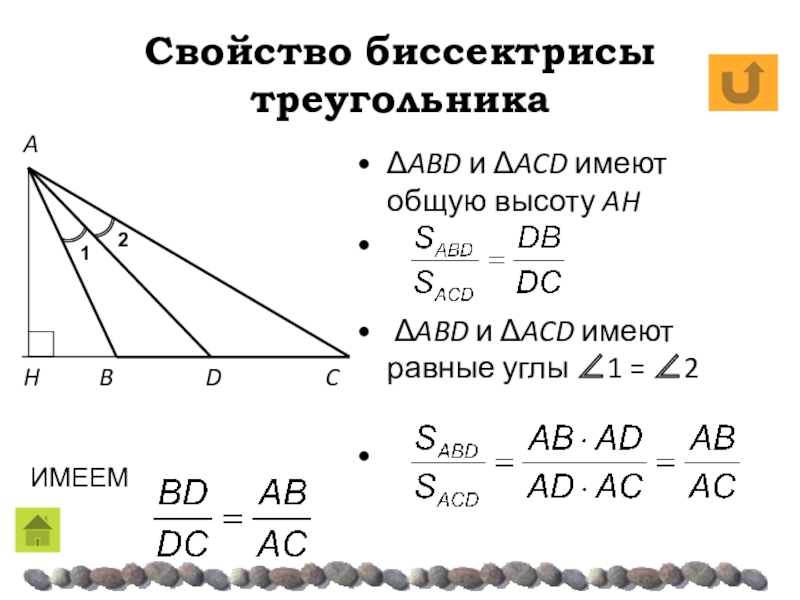
- 17. Свойство биссектрисы треугольникаΔABD и ΔACD имеют общую
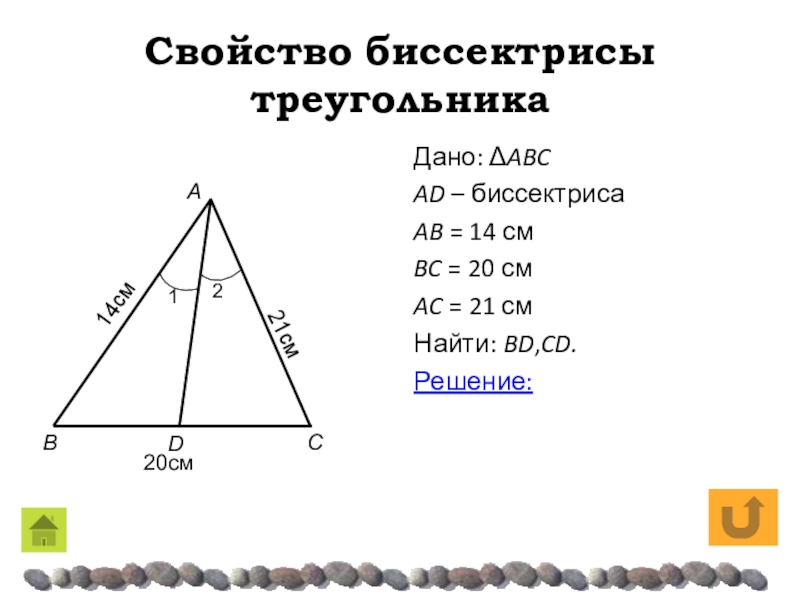
- 18. Свойство биссектрисы треугольникаДано: ΔABC AD – биссектрисаAB
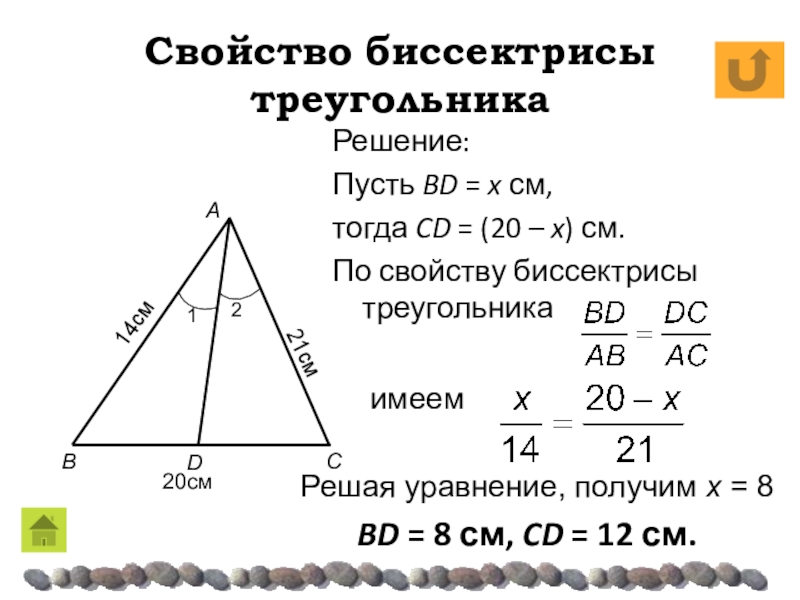
- 19. Свойство биссектрисы треугольникаРешение:Пусть BD = x см,
- 20. Признаки подобия треугольниковПервый признак подобия треугольников.(по двум
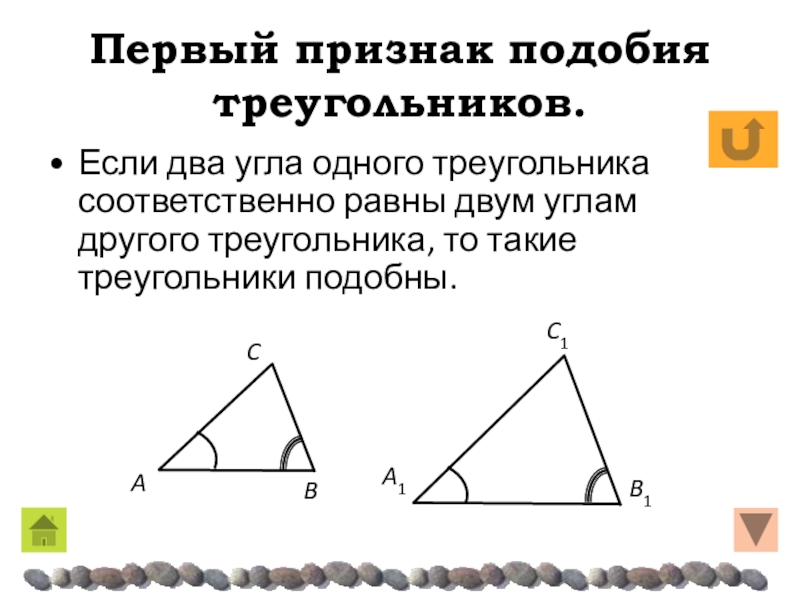
- 21. Первый признак подобия треугольников.Если два угла одного
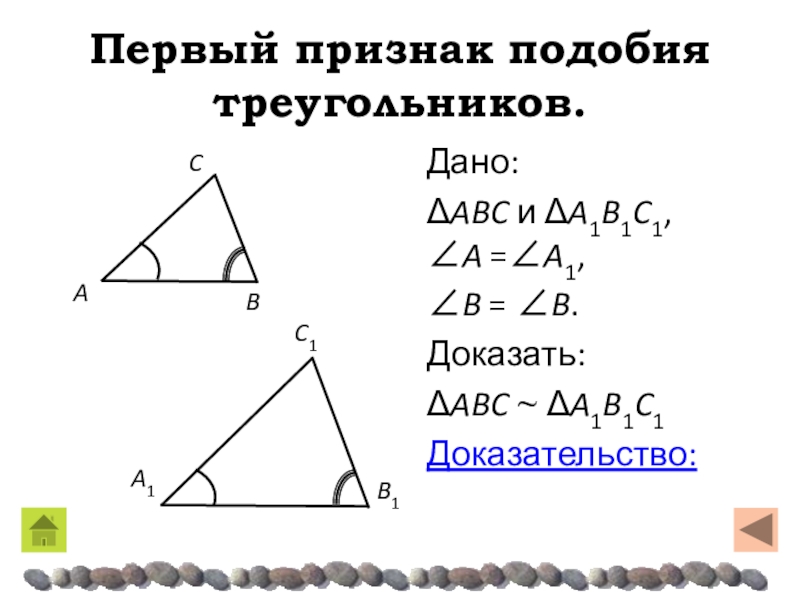
- 22. Первый признак подобия треугольников.Дано:ΔABC и ΔA1B1C1, A =A1,B = B.Доказать:ΔABC ~ ΔA1B1C1Доказательство:
- 23. Первый признак подобия треугольников.Доказательство: A =
- 24. Первый признак подобия треугольников.Доказательство: A =
- 25. Второй признак подобия треугольников. Если две стороны
- 26. Второй признак подобия треугольников. Дано:ΔABC и ΔA1B1C1, A =A1,Доказать:ΔABC ~ ΔA1B1C1Доказательство:
- 27. Второй признак подобия треугольников. Доказательство:Достаточно доказать, что
- 28. Третий признак подобия треугольников. Если три стороны
- 29. Третий признак подобия треугольников. Дано:ΔABC и ΔA1B1C1, Доказать:ΔABC ~ ΔA1B1C1Доказательство:
- 30. Третий признак подобия треугольников. Доказательство:Достаточно доказать, что
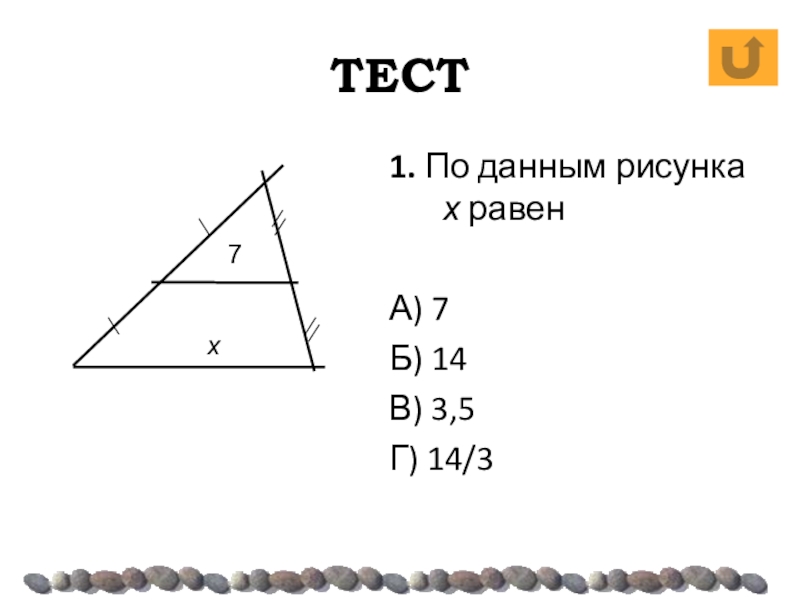
- 31. ТЕСТ1. По данным рисунка х равенА) 7Б) 14В) 3,5Г) 14/3
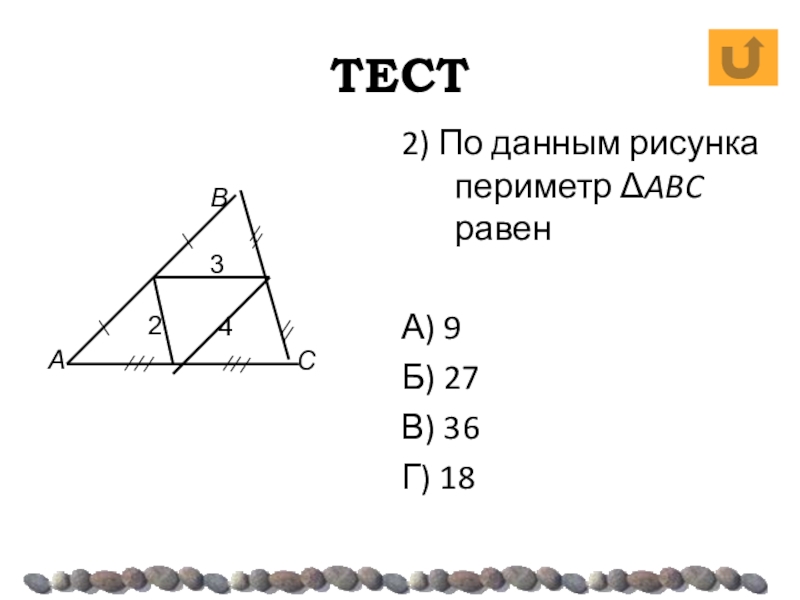
- 32. ТЕСТ2) По данным рисунка периметр ΔABC равенА) 9Б) 27В) 36Г) 18
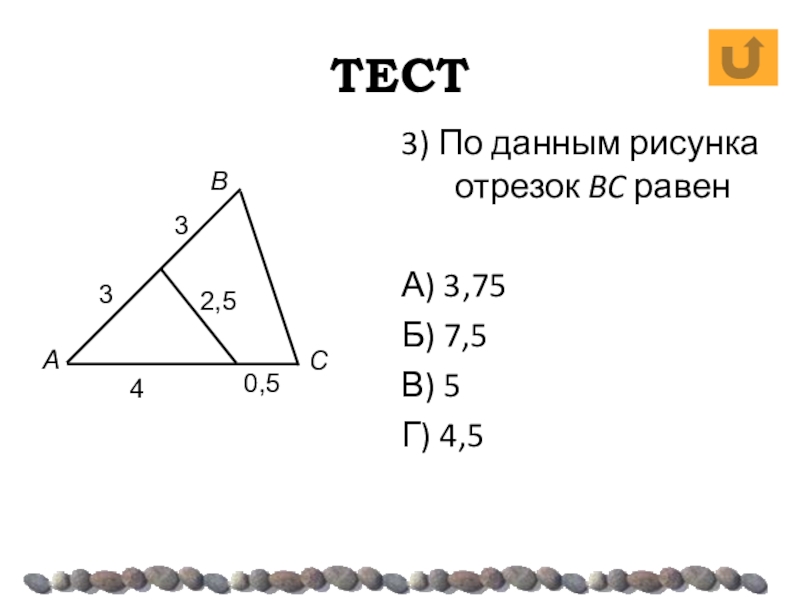
- 33. ТЕСТ3) По данным рисунка отрезок BC равенА) 3,75Б) 7,5В) 5Г) 4,5АВС3340,52,5
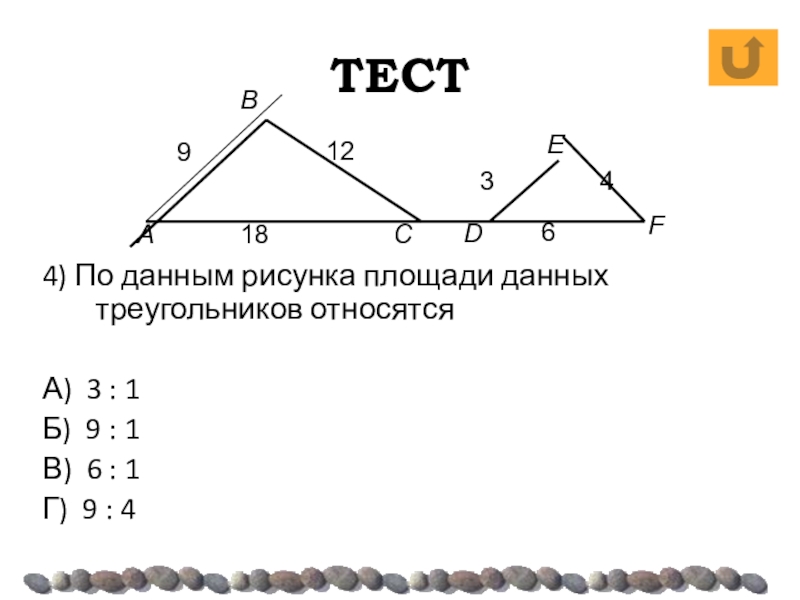
- 34. ТЕСТ4) По данным рисунка площади данных треугольников
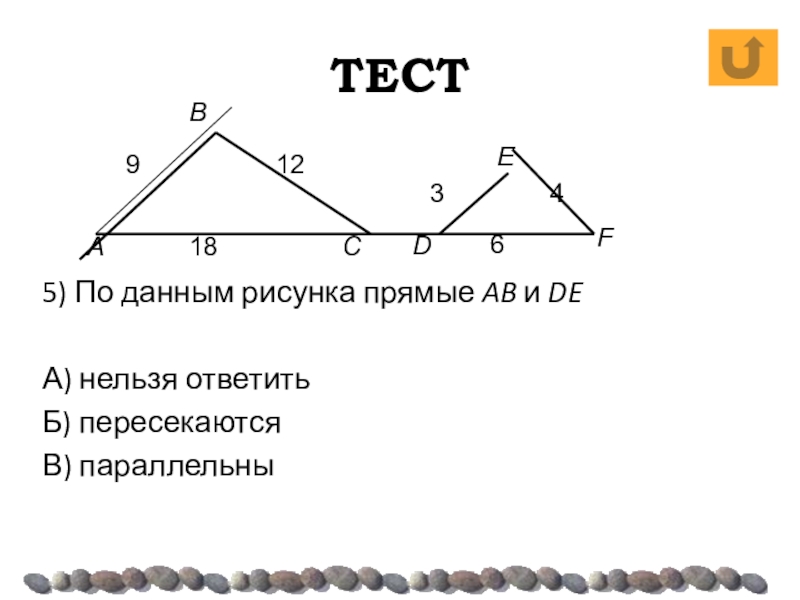
- 35. ТЕСТ5) По данным рисунка прямые AB и DEА) нельзя ответитьБ) пересекаютсяВ) параллельны
- 36. Скачать презентанцию
ПЛАНПропорциональные отрезки.Свойство биссектрисы треугольника.Определение подобных треугольников.Отношение периметров подобных фигур.Отношение площадей подобных фигур.Признаки подобия треугольников.
Слайды и текст этой презентации
Слайд 2ПЛАН
Пропорциональные отрезки.
Свойство биссектрисы треугольника.
Определение подобных треугольников.
Отношение периметров подобных фигур.
Отношение площадей
подобных фигур.
Слайд 3Пропорциональные отрезки
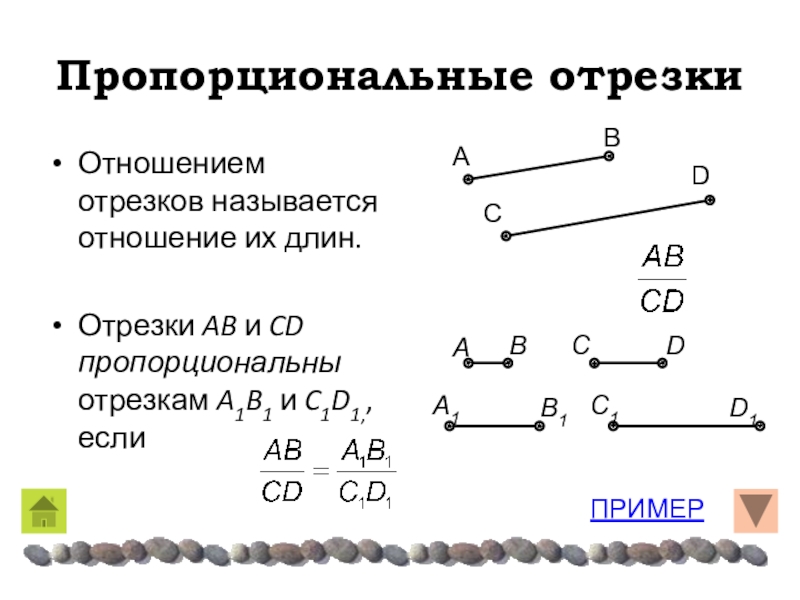
Отношением отрезков называется отношение их длин.
Отрезки AB и CD
пропорциональны отрезкам A1B1 и C1D1,, если
ПРИМЕР
Слайд 4ПРИМЕР
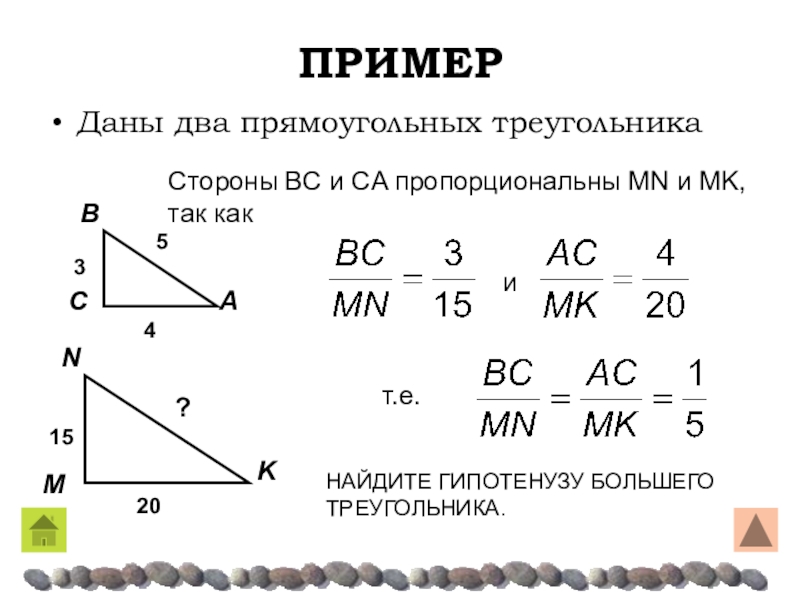
Даны два прямоугольных треугольника
Стороны ΒC и CA пропорциональны MN и
MK, так как
т.е.
и
НАЙДИТЕ ГИПОТЕНУЗУ БОЛЬШЕГО ТРЕУГОЛЬНИКА.
Слайд 5Пропорциональность отрезков
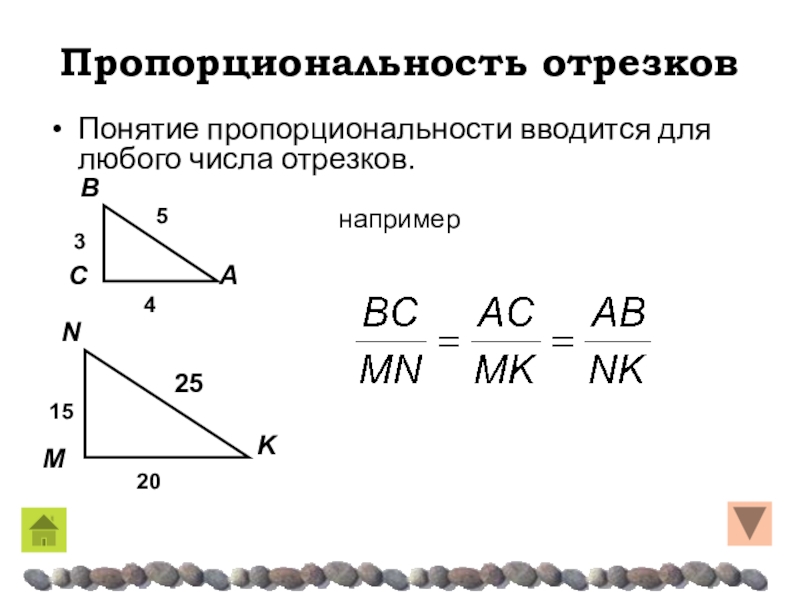
Понятие пропорциональности вводится для любого числа отрезков.
например
Слайд 6Подобные фигуры
Предметы одинаковой формы, но разных размеров
Фотографии, отпечатанные с одного
негатива, но с разными увеличениями;
Здание и его макет
Планы, географические карты одного и того же района, выполненные в разных масштабах.
Слайд 7Подобные фигуры
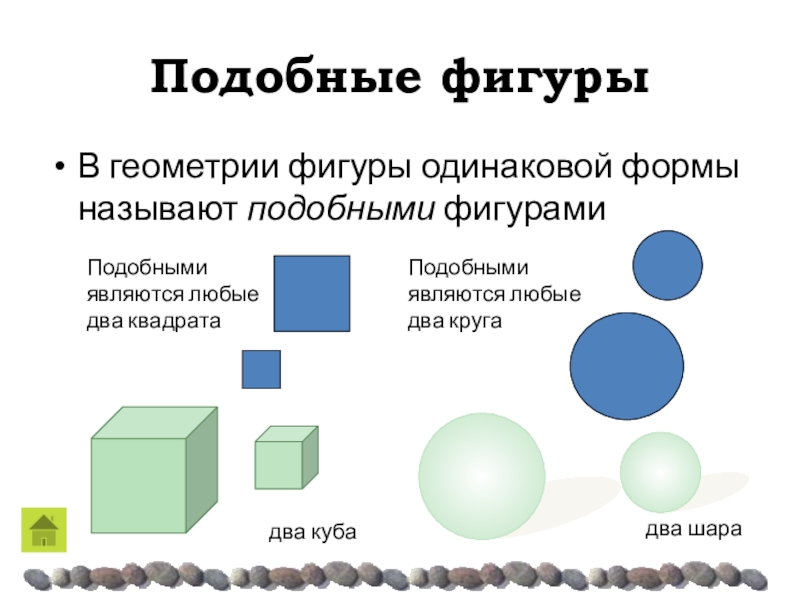
В геометрии фигуры одинаковой формы называют подобными фигурами
Подобными являются
любые два квадрата
Подобными являются любые два круга
два куба
два шара
Слайд 8Подобные треугольники
Даны два треугольника AΒC и A1Β1C1,
у которых A =
A1, Β = Β1, C = C1.
Стороны AΒ и A1Β1
, AC и A1C1 , ΒC и Β1C1, лежащие против равных углов, называют сходственными
Слайд 9Определение
Два треугольника называются подобными, если их углы соответственно равны и
стороны одного треугольника пропорциональны сходственным сторонам другого.
A = A1,
Β = Β1, C = C1.ΔAΒC ~ ΔA1Β1C1
Слайд 10Коэффициент подобия
Число k , равное отношению сходственных сторон, называется коэффициентом
подобия.
ΔAΒC ∞ ΔA1Β1C1
k – коэффициент подобия.
Слайд 11Дополнительные свойства
Отношение высот подобных треугольников, проведенных к сходственным сторонам, равно
коэффициенту подобия.
Отношение медиан подобных треугольников, проведенных к сходственным сторонам, равно
коэффициенту подобия. Отношение биссектрис подобных треугольников, проведенных к сходственным сторонам, равно коэффициенту подобия.
Слайд 12Отношение периметров
Отношение периметров подобных треугольников равно
коэффициенту подобия.
ΔAΒC ~ ΔA1Β1C1
ДОКАЗАТЕЛЬСТВО
Слайд 14Отношение площадей
Отношение площадей подобных треугольников равно квадрату коэффициента подобия.
ΔAΒC ~
ΔA1Β1C1
ДОКАЗАТЕЛЬСТВО
Слайд 15Отношение площадей
Пусть ΔAΒC ~ ΔA1Β1C1,
коэффициент подобия k
A = A1,
по теореме об отношении площадей треугольников, имеющих по равному углу,
имеем
Слайд 16Свойство биссектрисы треугольника
C
B
A
Биссектриса треугольника делит противоположную сторону на отрезки,
пропорциональные прилежащим сторонам треугольника.
D
или
ДОКАЗАТЕЛЬСТВО
ПРИМЕР
Слайд 17Свойство биссектрисы треугольника
ΔABD и ΔACD имеют общую высоту AH
ΔABD и ΔACD имеют равные углы 1 = 2
ИМЕЕМ
Слайд 18Свойство биссектрисы треугольника
Дано: ΔABC
AD – биссектриса
AB = 14 см
BC
= 20 см
AC = 21 см
Найти: BD,CD.
Решение:
Слайд 19Свойство биссектрисы треугольника
Решение:
Пусть BD = x см,
тогда CD =
(20 – x) см.
По свойству биссектрисы треугольника
имеем
Решая уравнение, получим
х = 8BD = 8 см, CD = 12 см.
Слайд 20Признаки подобия треугольников
Первый признак подобия треугольников.
(по двум углам)
Второй признак подобия
треугольников.
(по углу и двум пропорциональным сторонам)
Третий признак подобия треугольников.
(по трем
пропорциональным сторонам)
Слайд 21Первый признак подобия треугольников.
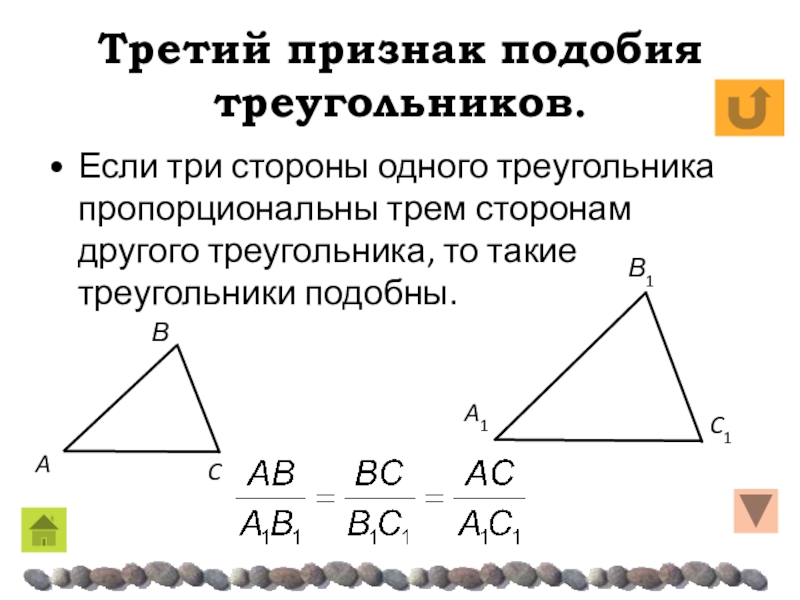
Если два угла одного треугольника соответственно равны
двум углам другого треугольника, то такие треугольники подобны.
Слайд 22Первый признак подобия треугольников.
Дано:
ΔABC и ΔA1B1C1, A =A1,
B = B.
Доказать:
ΔABC
~ ΔA1B1C1
Доказательство:
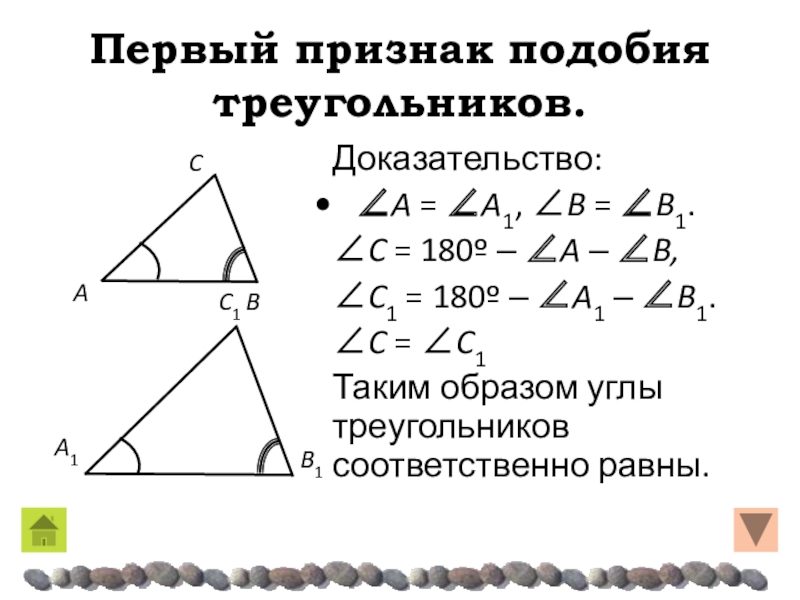
Слайд 23Первый признак подобия треугольников.
Доказательство:
A = A1, B
= B1.
C = 180º – A – B,
C1 = 180º
– A1 – B1.C = C1
Таким образом углы треугольников соответственно равны.
Слайд 24Первый признак подобия треугольников.
Доказательство:
A = A1,
B = B1.
Имеем
Аналогично, рассматривая равенство углов C=C1, A=A1,
получимИтак, сходственные стороны пропорциональны.
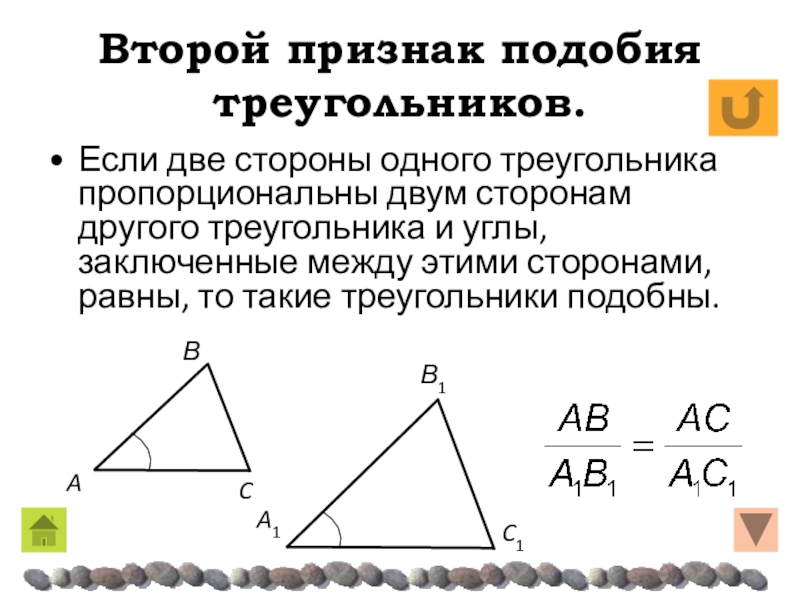
Слайд 25Второй признак подобия треугольников.
Если две стороны одного треугольника пропорциональны
двум сторонам другого треугольника и углы, заключенные между этими сторонами,
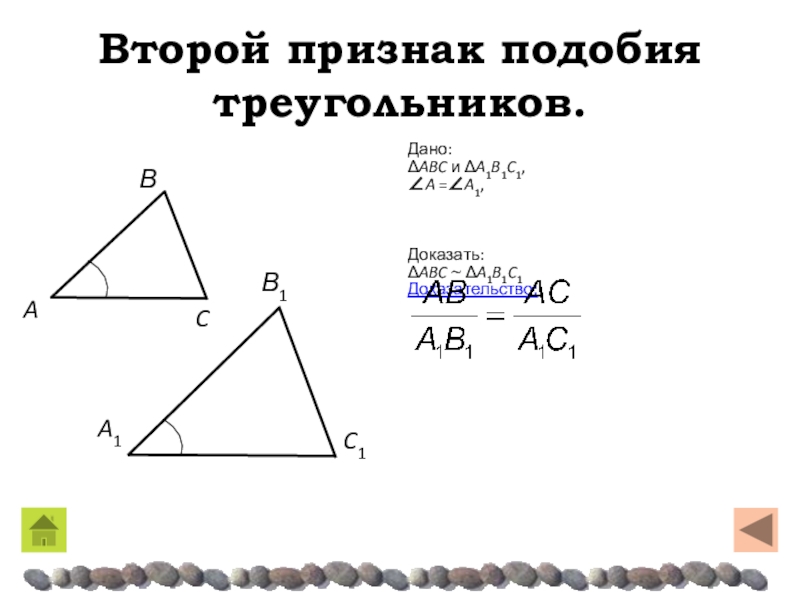
равны, то такие треугольники подобны.
Слайд 26Второй признак подобия треугольников.
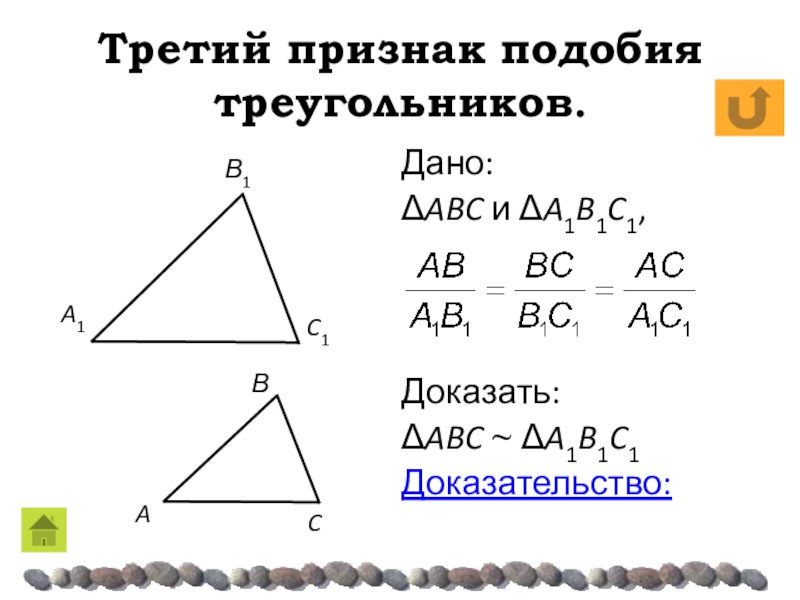
Дано:
ΔABC и ΔA1B1C1,
A =A1,
Доказать:
ΔABC ~
ΔA1B1C1
Доказательство:
Слайд 27Второй признак подобия треугольников.
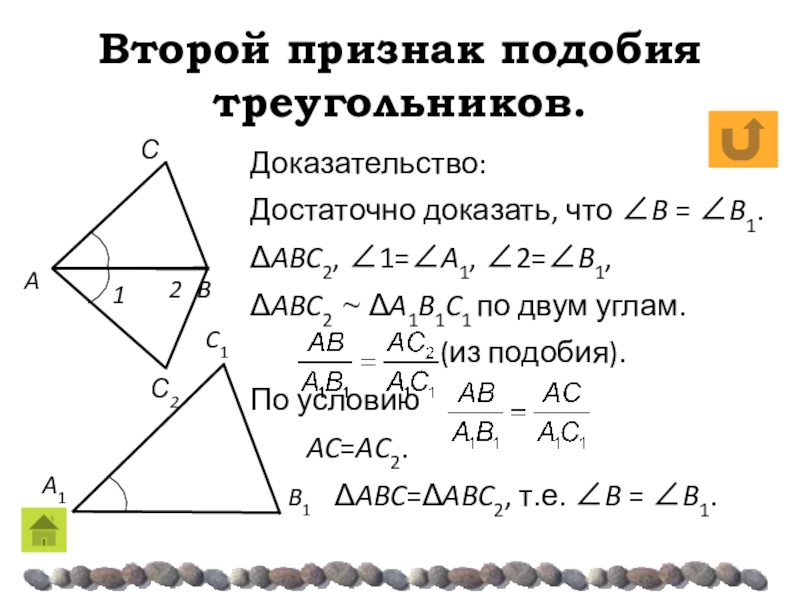
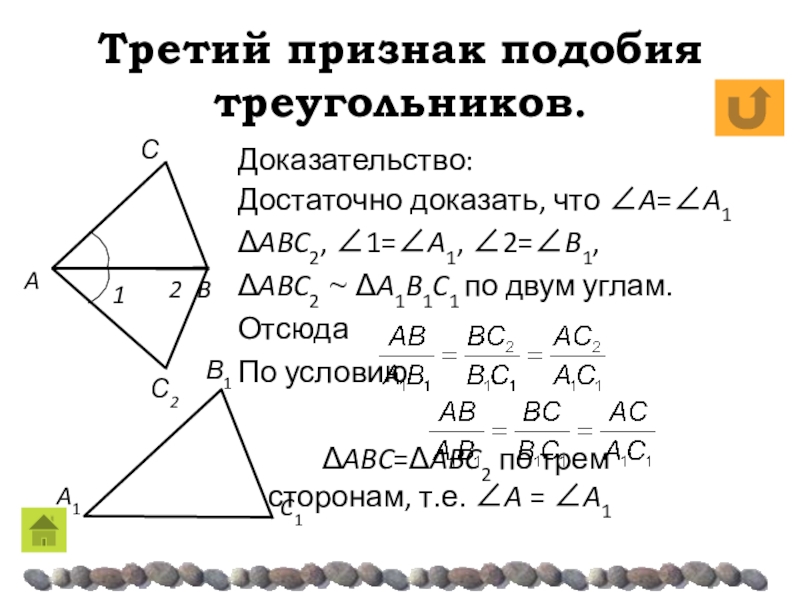
Доказательство:
Достаточно доказать, что B = B1.
ΔABC2,
1=A1, 2=B1,
ΔABC2 ~ ΔA1B1C1 по двум углам.
(из подобия).По условию
AC=AC2.
ΔABC=ΔABC2, т.е. B = B1.
Слайд 28Третий признак подобия треугольников.
Если три стороны одного треугольника пропорциональны
трем сторонам другого треугольника, то такие треугольники подобны.
Слайд 29Третий признак подобия треугольников.
Дано:
ΔABC и ΔA1B1C1,
Доказать:
ΔABC ~ ΔA1B1C1
Доказательство:
Слайд 30Третий признак подобия треугольников.
Доказательство:
Достаточно доказать, что A=A1
ΔABC2, 1=A1, 2=B1,
ΔABC2
~ ΔA1B1C1 по двум углам.
Отсюда
По условию
ΔABC=ΔABC2 по трем сторонам, т.е. A = A1
Слайд 34ТЕСТ
4) По данным рисунка площади данных треугольников относятся
А) 3
: 1
Б) 9 : 1
В) 6 : 1
Г) 9 :
4
