Слайд 14) Полюсное условие заключается в том, что длина одной и
той же стороны, вычисленная двумя независимыми путями по уравненным углам
должна иметь в обоих случаях одинаковое значение.
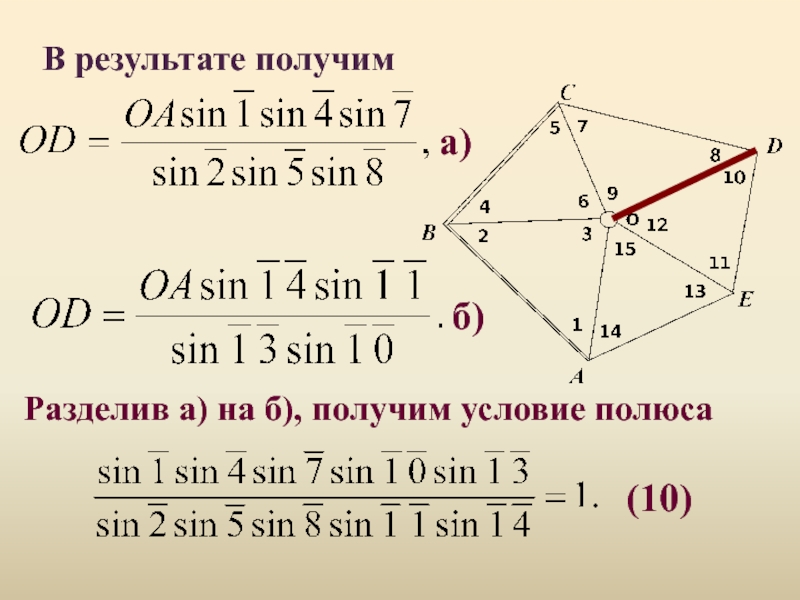
Возьмем в качестве исходной сторону ОА и вычислим дважды сторону ОD, решая треугольники по часовой стрелке и против часовой стрелки.
Слайд 2а)
б)
(10)
В результате получим
Разделив а) на б), получим
условие полюса
Слайд 3Равенство (10) можно получить, решая треугольники по ходу часовой стрелки,
начиная от стороны OA и кончая стороной OA.
Все стороны имеют
общую точку О, называемую полюсом.
Для перехода к условным уравнениям поправок в уравнении (10) необходимо заменить уравненные углы измеренными с поправками и привести его к линейному виду, разложив в ряд Тейлора, ограничиваясь первыми степенями поправок.
Слайд 5Если второе слагаемое умножить и разделить на sin1, то его
с достаточной точностью можно заменить значением
. Аналогично мож-но преобразовать и другие слагаемые.
Введем следующие обозначения
Слайд 6Тогда полюсное условное уравнение поправок в угловой мере будет иметь
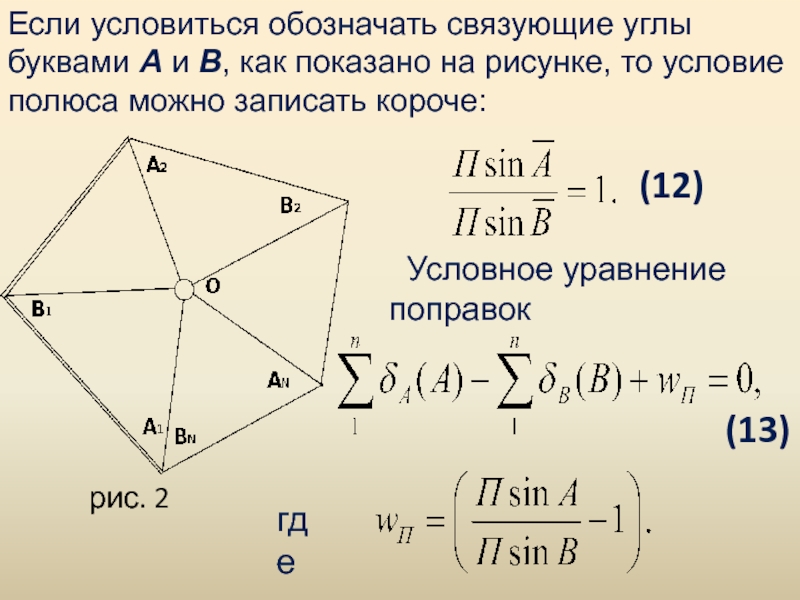
Слайд 7Если условиться обозначать связующие углы буквами А и В, как
показано на рисунке, то условие полюса можно записать короче:
(12)
Условное уравнение
поправок
(13)
где
рис. 2
Слайд 85) Условие сторон (базисов) заключается в том, что длина одной
исходной стороны, вычисленная по другой исходной стороне и уравненным углам
должна быть равна известному ее значению.
рис. 3
Слайд 9Для данной цепи треугольников, заключенной между исходными сторонами b1 и
b2 можно записать
или в другом виде
(14)
Слайд 10Это равенство и будет выражать условие сторон. Оно аналогично (10).
Для перехода к условному уравнению поправок необходимо поступить так, как
в предыдущем случае. В результате получим
, (15)
Слайд 11где
(16)
Если связующие углы числителя обозначить через А, а в знаменателе
через В, то выражения (14), (15) и (16) можно записать
короче:
(17)
Слайд 12(18)
(19)
6) Условие дирекционных углов заключается в том, что дирекционный угол
одной исходной стороны, вычисленный по дирекционному углу другой исходной стороны
и уравненным углам должен быть равен известному его значению.
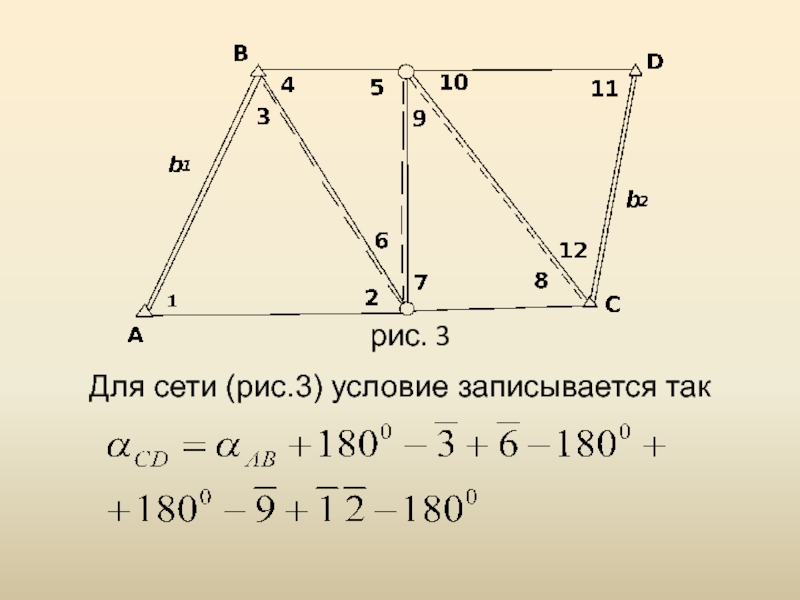
Слайд 13Для сети (рис.3) условие записывается так
рис. 3
Слайд 14Заменим уравненные углы измеренными c поправками
αAB–[3+(3)]+[6+(6)]–[9+(9)]+[12+(12)]– αСD=0.
Обозначим
wα = αAB
–3 + 6 – 9 + 12 – αСD. (20)
Тогда
условное уравнение поправок примет вид:
–(3) + (6) – (9) + (12) + wα = 0. (21)
Слайд 157) Условие координат заключается в том, что координаты исходной точки
вычисленные по уравненным углам и координатам другой исходной точки должны
быть равны известному значению. Условия абсцисс и ординат возникают тогда, когда в сети можно выделить ход, заключенный между двумя исходными пунктами.
Слайд 16рис. 3
В сети (рис. 3), можно наметить ход между точками
В и С, показанный пунктиром.
(22)
Условные уравнения координат в сокращен-ном виде можно записать так
(22)
Слайд 17Здесь (Δх) и (Δу) – поправки в прираще-ния координат, а
wx и wy свободные члены (невязки), вычисляемые по формулам
(23)
В
окончательном виде поправки должны находиться к углам.
Общее число независимых условных уравнений в сети триангуляции и, в том числе по видам, определяется по схеме сети.
Слайд 186. Допустимые размеры свободных членов условных уравнений
Размеры свободных членов
условных уравнений зависят от точности полевых измерений, ошибок исходных данных
и формы сетей.
Если ошибками исходных данных пренебречь, то невязки будут являться функциями измеренных величин:
w = f(l1, l2, … ln).
Слайд 19По правилам теории ошибок измерений
где f – частные производные (коэффициенты
при поправках в условных уравнениях);
т – СКО измерений.
При равноточных
измерениях
Слайд 20Принимая зависимость
Δпр = 2,5 m,
получим
С учетом ошибок исходных данных применительно
к триангуляции предельные невязки найдутся по формулам
1. Для полюсных
условий
Слайд 212. Для условия сторон
3. Для дирекционных углов
4. Для условий фигур
и горизонтов
Слайд 22В этих формулах:
т – СКО измерения угла по инструкции;
[δ2]
– сумма квадратов коэффициентов δ;
ms – СКО исходных сторон;
mα
– СКО исходных дирекционных углов;
n – число углов.
Слайд 23Тема:
«ПОНЯТИЕ О СПОСОБАХ УРАВНИВАНИЯ»
Слайд 24 Сущность уравнивания геоде-зических измерений по методу наименьших квадратов.
Понятие
о коррелатном способе уравнивания.
Понятие о параметрическом способе уравнивания.
Слайд 253. Сущность уравнивания геодезических измерений по методу наименьших квадратов.
Избыточные измерения
приводят к многозначности решений. Если для вычисления одной и той
же величины использовать разные измеренные величины, то ввиду погрешностей измерений получим разные результаты.
Слайд 26Чтобы ликвидировать многозначность решений и привести результаты измерений в соответствие
с теорией в измеренные величины вводятся поправки. Исправление измеренных величин
называется уравниванием.
Задача уравнивания заключается в том, чтобы, используя все измерения, получить однозначно наиболее надежное значение всех неизвестных величин и оценить их точность.
Слайд 27В общем виде уравненное значение измеренных величин получают по формуле
xi=li+vi,
(1)
где li – результат измерения;
vi – поправка.
При отсутствии систематических ошибок
наиболее точные результаты достигаются при уравнивании по методу наименьших квадратов.
Слайд 28Если измерения равноточные, то поправки находятся под условием
[v2]
= min, (2)
если измерения неравноточные, то под условием
[p v2] = min. (3)
Слайд 29Метод наименьших квадратов дает однозначное решение при нахождении поправок.
Наличие
вторых степеней vi ограничивает крупные поправки, поэтому при равноточных измерениях
поправки распределяются более или менее равномерно.
При неравноточных измерениях веса pi при vi уменьшают поправки к более точным измерениям и увеличивают к менее точным.
Слайд 30Совместное уравнивание измерений нескольких величин по методу наименьших квадратов является
задачей на условный экстремум. Для ее решения применяют два основных
способа:
Способ Лагранжа с неопределенными множителями (коррелатный способ).
Способ абсолютного экстремума (параметрический способ).
Слайд 314. Понятие о коррелатном способе уравнивания.
Пусть измерено n величин, истинное
значение которых Х1, Х2, …, Хn. Обозначим результаты измерений через
l1, l2, …, ln. Если в числе измерений имеется r избыточных, то искомые неизвестные будут связаны r независимыми условиями
(4)
Слайд 32Здесь x1, x2, …, xn уравненные значения измеренных величин. Выражения
(4) называются условными уравнениями. Они могут быть в линейном и
нелинейном виде.
Для приведения их к линейному виду необходимо заменить уравненные значения измеренными с поправками согласно (1), т.е. xi=li+vi и разложить каждую функцию в ряд Тейлора.
Слайд 33В результате получим условные уравне-ния поправок в следующем линейном виде
где a, b ,
… r – частные производные;
w – свободные члены (невязки).
(5)
Слайд 34Выражение (5) можно упростить
(6)
Особенность уравнений поправок в том, что число их меньше числа неизвестных (r < n). Поэтому система неопределенная, допускающая множество решений.
Слайд 35Рассмотрим решение задачи по определению поправок для случая равноточных измерений
в соответствии с принципом [v2] = min, т.е. будем находить
[v2] = min при условии (6).
Данная задача решается с помощью множителей Лагранжа.
Слайд 36
(7)
Составим функцию путем прибавления к [v2] левых частей уравнения
(6), умножив каждое на неопределенный множитель –2k1, –2k2,…, –2kr
Слайд 37Для нахождения минимума функции (7) находят частные производные и приравнивают
к нулю. В результате получим n уравнений:
Слайд 38Отсюда получим уравнения поправок
(8)
Неопределенные множители
k1, k2, …, kr называются коррелатами. Чтобы по этим уравнениям найти поправки, нужно вначале определить эти коррелаты.
Слайд 39Подставляя выражения из (8) в услов-ные уравнения (5) для первого
уравнения получим
а1а1k1+a1b1k2+…+a1r1kr+
а2а2k1+a2b2k2+…+a2r2kr+
+………+
+аnаnk1+anbnk2+…+anrnkr+w1=0,
или
[aa]k1+[ab]k2+…+[ar]kr+ w1=0.
Слайд 40Делая аналогичную подстановку в остальные уравнения системы (5), получим систему
нормальных уравнений коррелат в следующем виде
(9)
Слайд 41Коэффициенты [aa], [bb], …., [rr], распо-ложенные на главной диагонали, всегда
положительны и называются квадратич-ными. Неквадратичные коэффициенты, расположенные симметрично относительно главной
диагонали попарно равны между собой. Поэтому для краткости нормальные уравнения, обычно, записывают, начиная с квадратичных коэффициентов.
Решая систему (9) находят коррелаты, а затем, подставляя в уравнения поправок (8) находят поправки к измеренным величинам.
Слайд 42Для неравноточных измерений уравне-ния поправок имеют вид
Слайд 43Нормальные уравнения коррелат будут такими
(11)
В этих выражениях q – величина
обратная весу измерения
Вывод аналогичен, только условие [v2] = min заменяется на [pv2] = min.
![Заменим уравненные углы измеренными c поправкамиαAB–[3+(3)]+[6+(6)]–[9+(9)]+[12+(12)]– αСD=0. Обозначимwα = αAB –3 + 6 – 9 + 12](/img/thumbs/860fef0f113d3742ea7be97b4f55e13d-800x.jpg "Полюсное условие Заменим уравненные углы измеренными c поправкамиαAB–[3+(3)]+[6+(6)]–[9+(9)]+[12+(12)]– αСD=0. Обозначимwα = αAB –3")
![В этих формулах:т – СКО измерения угла по инструкции; [δ2] – сумма квадратов коэффициентов δ; ms –](/img/thumbs/02a12a04ab16b6729eeecdc65468074c-800x.jpg "Полюсное условие В этих формулах:т – СКО измерения угла по инструкции; [δ2] –")
![Если измерения равноточные, то поправки находятся под условием [v2] = min, (2)если измерения неравноточные, то под](/img/thumbs/8a7ea83e0ec579226f2da385d77d2031-800x.jpg "Полюсное условие Если измерения равноточные, то поправки находятся под условием [v2] = min,")
![Рассмотрим решение задачи по определению поправок для случая равноточных измерений в соответствии с принципом [v2] = min,](/img/thumbs/2c8dedcbfdcb4e68d65f924b038755c6-800x.jpg "Полюсное условие Рассмотрим решение задачи по определению поправок для случая равноточных измерений в")
![(7)Составим функцию путем прибавления к [v2] левых частей уравнения (6), умножив каждое на неопределенный множитель –2k1,](/img/thumbs/c21bdedc8490384a795b68ad1270a6fb-800x.jpg "Полюсное условие (7)Составим функцию путем прибавления к [v2] левых частей уравнения (6),")
![Подставляя выражения из (8) в услов-ные уравнения (5) для первого уравнения получим а1а1k1+a1b1k2+…+a1r1kr+а2а2k1+a2b2k2+…+a2r2kr++………++аnаnk1+anbnk2+…+anrnkr+w1=0,или [aa]k1+[ab]k2+…+[ar]kr+ w1=0.](/img/thumbs/a83a944f4da670ade2bb15f545d97e04-800x.jpg "Полюсное условие Подставляя выражения из (8) в услов-ные уравнения (5) для первого уравнения получим а1а1k1+a1b1k2+…+a1r1kr+а2а2k1+a2b2k2+…+a2r2kr++………++аnаnk1+anbnk2+…+anrnkr+w1=0,или [aa]k1+[ab]k2+…+[ar]kr+ w1=0.")
![Коэффициенты [aa], [bb], …., [rr], распо-ложенные на главной диагонали, всегда положительны и называются квадратич-ными. Неквадратичные коэффициенты, расположенные](/img/thumbs/f82c2dcc88c2a4177243eec87f899f4e-800x.jpg "Полюсное условие Коэффициенты [aa], [bb], …., [rr], распо-ложенные на главной диагонали, всегда положительны")
