Слайд 1Дисциплина:
«Автоматизированный электрический привод»
Лекция № 4:
МЕХАНИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЭЛЕКТРОДВИГАТЕЛЕЙ ПОСТОЯННОГО
ТОКА
В ДВИГАТЕЛЬНОМ И ТОРМОЗНЫХ РЕЖИМАХ
Доцент кафедры к. т. н.
ГОРПИНЧЕНКО
Александр Владимирович
СЕВАСТОПОЛЬСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Кафедра «ВОЗОБНОВЛЯЕМЫЕ ИСТОЧНИКИ ЭНЕРГИИ И ЭЛЕКТРИЧЕСКИЕ СИСТЕМЫ И СЕТИ»
Слайд 21. Уравнения электромеханической и механической характеристик ЭД независимого возбуждения в
двигательном режиме.
2. Механические характеристики ЭД независимого возбуждения при уменьшении магнитного
потока.
3. Механические характеристики ЭД независимого возбуждения при изменении напряжения питания.
4. Механические характеристики ЭД независимого возбуждения в тормозных режимах.
1
ВОПРОСЫ
ЛИТЕРАТУРА
М.Г.Чиликин, А.С.Сандлер
«Общий курс электропривода», стр. 29…31, 58...65.
Слайд 32
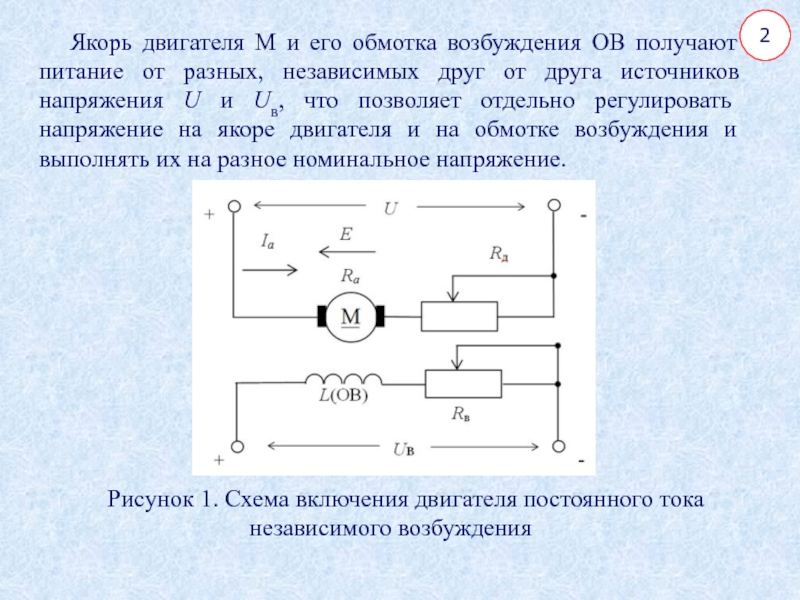
Якорь двигателя М и его обмотка возбуждения ОВ получают питание
от разных, независимых друг от друга источников напряжения U и
Uв, что позволяет отдельно регулировать напряжение на якоре двигателя и на обмотке возбуждения и выполнять их на разное номинальное напряжение.
Рисунок 1. Схема включения двигателя постоянного тока независимого возбуждения
Слайд 43
Направления тока I и ЭДС вращения двигателя Е, соответствуют
двигательному режиму работы, когда электрическая энергия потребляется двигателем из сети
и преобразуется в механическую энергию, мощность которой равна Р = М ∙ Ω.
Аналитическое выражение механической характеристики может быть получено из уравнения равновесия напряжений для цепи якоря ЭД (рис 1).
В установившемся режиме работы ЭД напряжение U уравновешивается ЭДС (наведенной в якоре) Е и падением напряжения на сопротивлениях цепи якоря.
U = E +Ia R , (1)
где: Ia - ток в якорной цепи двигателя, А
R = Ra+ Rд - суммарное сопротивление якорной цепи, Ом.
ЭДС определяется: Е = k ∙ Ω ∙ Ф, (2)
где: – конструктивный коэффициент (р – число пар полюсов двигателя; N - число активных проводников обмотки якоря;
а — число пар параллельных ветвей обмотки якоря);
Ф — магнитный поток двигателя, Вб
Ω — угловая скорость двигателя, рад/с.
Слайд 54
Подставив (2) в (1) получим выражение для скорости двигателя:
(3)
Уравнение (3) представляет собой зависимость скорости двигателя от тока якоря. Такую зависимость Ω=f(I) называют электромеханической характеристикой двигателя.
Для получения уравнения механической характеристики необходимо найти зависимость скорости от момента двигателя.
Момент, развиваемый двигателем, связан с током якоря и магнитным потоком простой зависимостью, а именно:
М = k∙Ф∙Iа (4)
Откуда , подставив его в уравнение (3) получим выражение
для механической характеристики:
(5)
Слайд 65
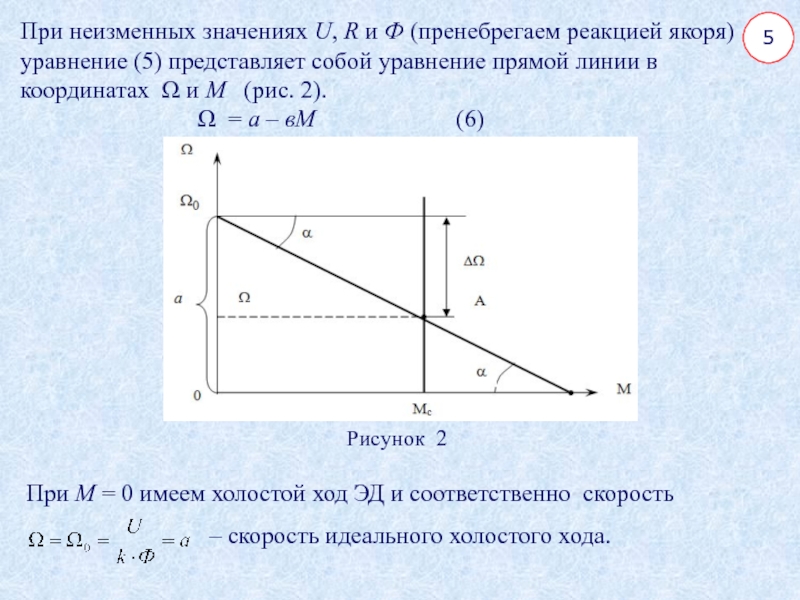
При неизменных значениях U, R и Ф (пренебрегаем реакцией
якоря) уравнение (5) представляет собой уравнение прямой линии в координатах
Ω и М (рис. 2).
Ω = a – вМ (6)
Рисунок 2
При М = 0 имеем холостой ход ЭД и соответственно скорость
– скорость идеального холостого хода.
Слайд 76
Поскольку Iа = 0, приложенное напряжение уравновешивается только Э.Д.С.,
U=E0= k∙ Ω0∙Ф .
Второй член выражения
(5) характеризует перепад скорости Ω относительно скорости идеального холостого хода Ω0 – ΔΩ
(7)
Коэффициент характеризует крутизну
механической характеристики, т.е. определят её жесткость.
Таким образом Ω = Ω0 – ΔΩ = Ω0 – tgα ∙ M (8)
Из выражения видно, что при неизменных
Ф и Rа крутизна, а значит и жесткость характеристик зависит только от величины Rд.
Слайд 87
Рисунок 3.
Естественной характеристикой называется такая характеристика двигателя, которая получается при
отсутствии внешних резисторов в якорной цепи и номинальных значениях напряжения
и магнитного потока двигателя.
Характеристики, получаемые при Rд > 0 называются искусственными (реостатными) характеристиками.
Слайд 98
Все характеристики будут иметь одну общую точку
(скорость идеального холостого
хода) при М = 0.
Наклон же характеристик будет зависеть от
Rд (чем больше значение Rд, тем мягче характеристика).
ЭД параллельного возбуждения имеет аналогичные электромеханические и механические характеристики если ЭД получает питание от мощной сети (U = сonst) и при пренебрежении реакцией якоря (Ф = сonst).
Слайд 109
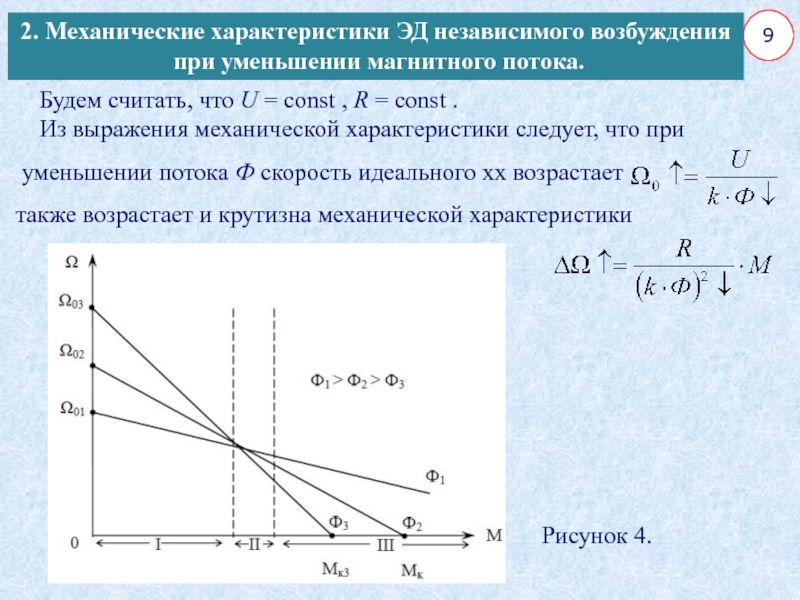
Будем считать, что U = сonst , R = сonst
.
Из выражения механической характеристики следует, что при
уменьшении потока Ф
скорость идеального хх возрастает
также возрастает и крутизна механической характеристики
Рисунок 4.
2. Механические характеристики ЭД независимого возбуждения
при уменьшении магнитного потока.
Слайд 1110
Ток стоянки (т.к. Ω
=0 и Е = k∙Ф∙Ω = 0) и не зависит
от Ф,
поэтому момент стоянки Мк = k ∙ Ф ∙ Iк пропорционален Ф.
Уменьшение Ф можно использовать для регулирования Ω. По оси моментов всё семейство механических характеристик может быть разбито на 3-и зоны:
– I-я зона. При Ф↓ Ω↑ возможно регулирование Ω ослаблением потока Ф.
– II-я зона. Ф = var не приводит к существенным изменению Ω .
– III-я зона. В ней лежат значения моментов, при которых Ф↓ и вызывает Ω ↓ (зона опрокидывания регулирования).
Слайд 1211
Будем считать, что R=const; Ф=const, а U можно регулировать. При
этом скорость будет изменяться пропорционально U:
, а крутизна характеристик будет неизменна, так как
не зависит от U.
Изменением U можем регулировать Ω.
Рисунок 5.
3. Механические характеристики ЭД независимого возбуждения
при изменении напряжения питания.
Слайд 1312
Во время торможения или реверса ЭД работает в одном из
тормозных режимов с соответствующей механической характеристикой.
Различают следующие тормозные режимы:
1) генераторное
торможение с отдачей энергии в сеть
(рекуперативное торможение);
2) торможение противовключением;
3) динамическое торможение.
Рассмотрим механические характеристики ЭД независимого возбуждения в тормозных режимах.
4. Механические характеристики ЭД независимого возбуждения
в тормозных режимах.
Слайд 1413
Рекуперативное торможение имеет место тогда, когда
скорость двигателя
оказывается выше скорости идеального холостого хода: Ω > Ω0 .
В этом случае двигатель начинает работать в режиме генератора, преобразовывая механическую энергию со стороны рабочего механизма в электрическую и отдавая её в сеть.
Ток изменяет своё направление, так как при Ω > Ω0 E > U.
, следовательно, изменяется знак и момент ЭД, т.е. он становится тормозным: М = – k∙Ф∙Iа.
Слайд 1514
Уравнение механической характеристики в режиме рекуперативного торможения имеет вид
(9)
Характеристика является продолжением характеристики двигательного режима во 2-м квадранте.
Генераторное торможение возможно в подъёмных механизмах при спуске груза и является весьма экономичным, так как сопровождается отдачей энергии в сеть.
Слайд 1716
Торможение противовключением осуществляется в том
случае, если под действием внешнего
момента или сил инерции двигатель вращается в сторону противоположную действию
электромагнитного момента.
Это может происходить, в приводе подъёмника. Когда двигатель включен на подъём, а момент развиваемый грузом заставляет привод вращаться в сторону спуска груза.
Такой же режим получается и при переключении обмотки двигателя для быстрой остановки на противоположное направление вращения.
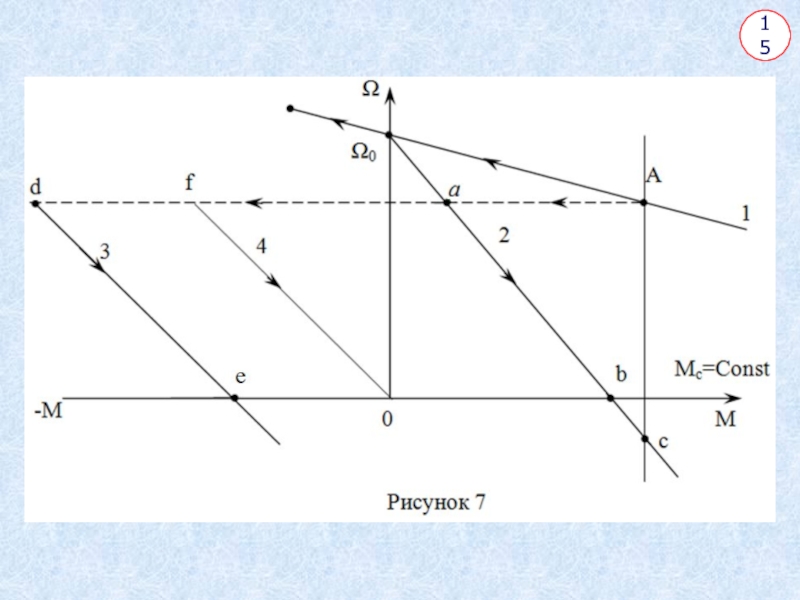
В первом случае (если при подъёме груза включить в цепь якоря резистор R ) торможение осуществляется по стрелке
А → а → b → c (рис.7) до установившейся скорости спуска в точку с, где Мт = Мс (прямая 2). Уравнение механической характеристики при этом имеет вид, как и для двигательного режима
(10)
Слайд 1817
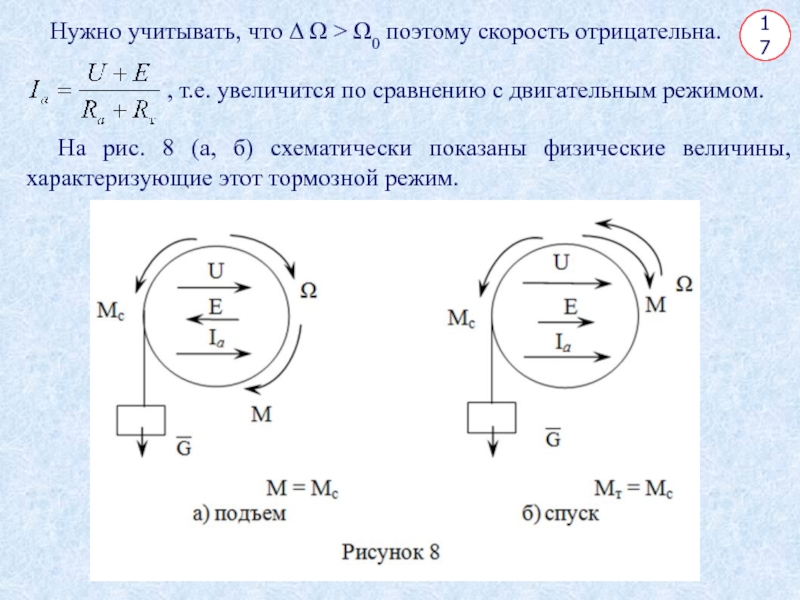
Нужно учитывать, что Δ Ω > Ω0 поэтому скорость отрицательна.
, т.е. увеличится по сравнению с двигательным режимом.
На рис. 8 (а, б) схематически показаны физические величины, характеризующие этот тормозной режим.
Слайд 1918
Если торможение осуществляется изменением полярности
на зажимах якоря с одновременным
включением резистора Rт , то характеристика изображается прямой (3) на
рис. 7.
Торможение осуществляется по стрелке A→ a → d → е.
В точке «е» ЭД необходимо отключить от сети, иначе произойдёт реверс.
Для этого случая уравнение механической характеристики будет
(11)
Слайд 2019
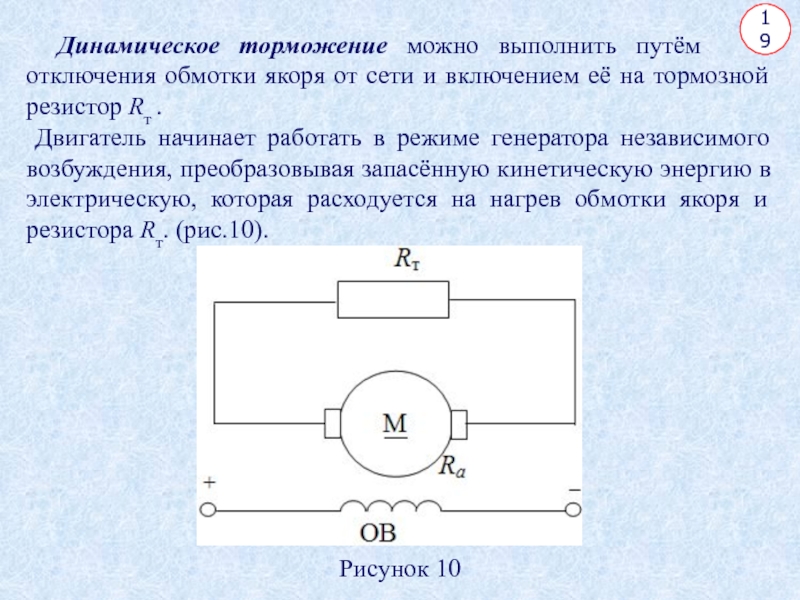
Динамическое торможение можно выполнить путём
отключения обмотки
якоря от сети и включением её на тормозной резистор Rт
.
Двигатель начинает работать в режиме генератора независимого возбуждения, преобразовывая запасённую кинетическую энергию в электрическую, которая расходуется на нагрев обмотки якоря и резистора Rт. (рис.10).
Рисунок 10
Слайд 2120
Так как U=0, то уравнение механической характеристики –(прямая 4) на
рис.7.
(12)
Ток якоря определяется по формуле
при этом Мт
= – k∙Ф∙Iа.
Торможение осуществляется по стрелке А → f → 0 (рис.7)
Рисунок 11