Понятие корреляционной зависимости

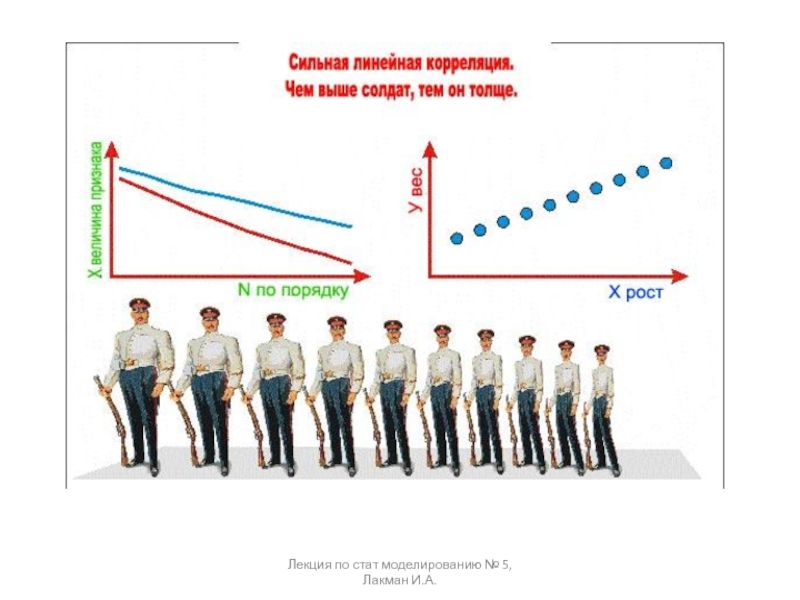
двумя или несколькими случайными величинами.
Определение. Зависимость случайных величин называют статистической,

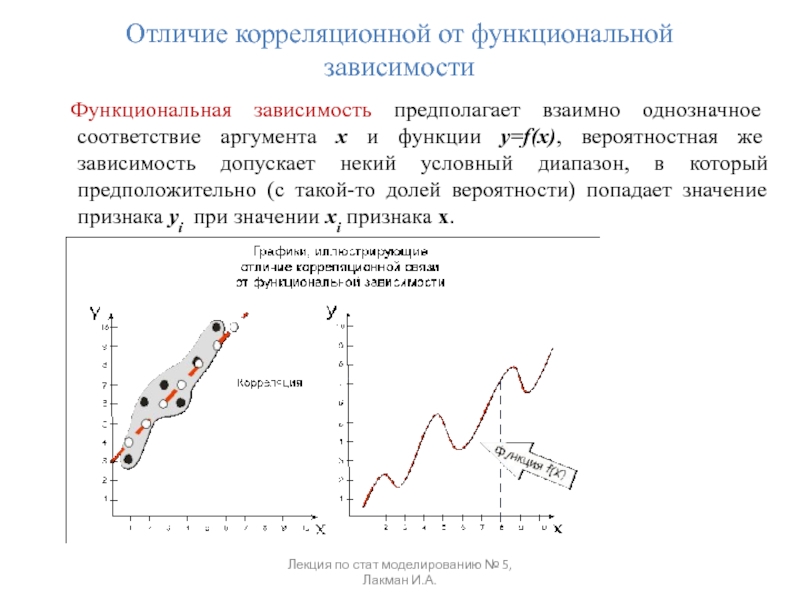
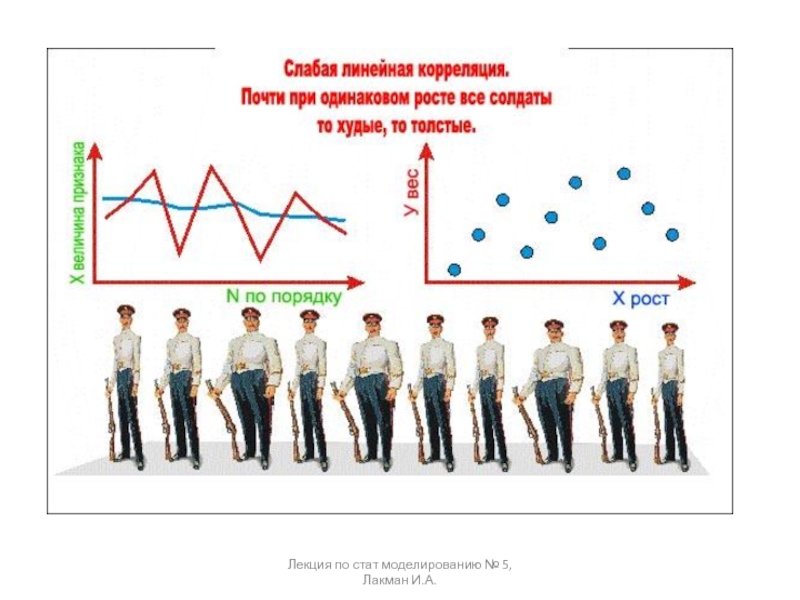
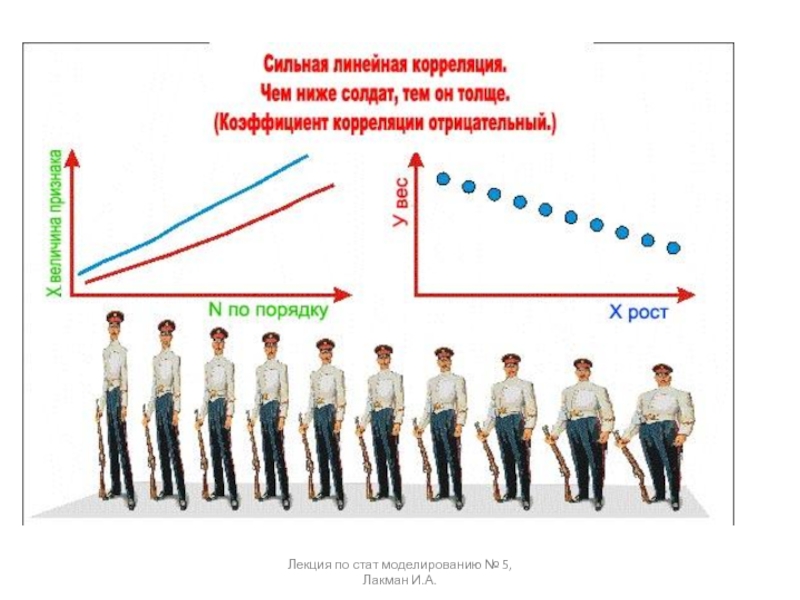
если изменение одной величины влечет изменение распределения другой величины.
Определение. Статистическая зависимость называется корреляционной, если при изменении одной величины изменяется среднее значение другой.
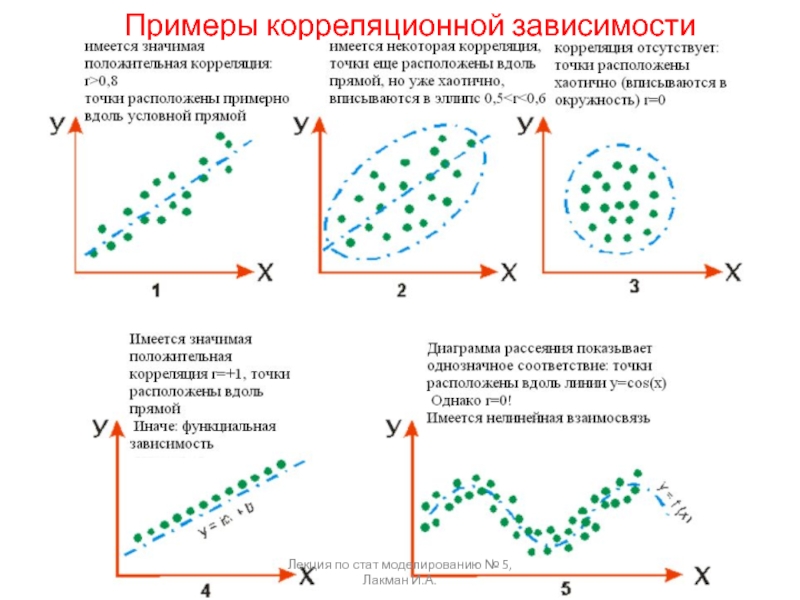
Если случайная величина представляет некоторый признак (например, статистические наблюдения некой экономической величины), то под корреляцией понимают – меру согласованности одного признака с другим, или с несколькими, либо взаимную согласованность группы признаков.

Лекция по стат моделированию № 5, Лакман И.А.

Однако, корреляционные методы не выявляют этой причинности, а лишь указывают

на наличие некоторого соответствия. Признаки могут находиться не только во взаимной зависимости друг от друга, но и оба зависеть от какого-либо третьего воздействия, не включенного в область рассмотрения. Например, между двумя временными рядами (переменные, состоящие из наблюдений отстоящих на равные промежутки времени друг от друга) может быть сильная корреляционная зависимость, однако эта зависимость будет ложной, так как переменные сами зависят от времени.
Таким образом, более корректно употреблять понятие корреляционная связь.

Лекция по стат моделированию № 5, Лакман И.А.

аргумента х и функции y=f(х), вероятностная же зависимость допускает некий

условный диапазон, в который предположительно (с такой-то долей вероятности) попадает значение признака уi при значении хi признака х.

Лекция по стат моделированию № 5, Лакман И.А.

признаками,


де хi — значения, принимаемые в выборке X,
yi

— значения, принимаемые в выборке Y;
— средняя по X, — средняя по Y.
Ведем обозначения: ковариация признаков X иY



Средние квадратичные отклонения и

Тогда:

Лекция по стат моделированию № 5, Лакман И.А.

0,50

положительный, то связь между признаками прямая: увеличение одного признака приводит к увеличению другого
Если коэффициент корреляции отрицательный, то связь между признаками обратная: увеличение одного признака приводит к уменьшению другого
В случае, если r=1, -1, то связь между признаками функциональная!

Лекция по стат моделированию № 5, Лакман И.А.

Лекция по стат моделированию №

5, Лакман И.А.

коэффициент корреляции Пиросона r незначимый;
Н1: коэффициент корреляции Пирсона r значим.
Расcчитывается

t-статистика по формуле:




Определяется tтабл по таблице Стьюдента со степенями свободы n-2 и уровнем значимости α
Если , то Н0 отклоняют на заданном уровне значимости, и считаем, что коэффициент корреляции Пирсона значимый.

Лекция по стат моделированию № 5, Лакман И.А.

точно, но он позволяет сравнить объекты между собой и расположить

их в порядке убывания или возрастания качества.
Под ранжированием будем понимать упорядочивание объектов согласно убыванию качественного признака
Для оценки степени связи качественных признаков используют коэффициенты ранговой корреляции.
Коэффициент корреляции Спирмена — мера линейной связи между случайными величинами. Корреляция Спирмена является ранговой, то есть для оценки силы связи используются не численные значения, а соответствующие им ранги.
Коэффициент корреляции Кендалла — мера линейной связи между случайными величинами

Лекция по стат моделированию № 5, Лакман И.А.

иерархии признаков будут участвовать в сопоставлении как переменные X и

Y.
Проранжировать значения переменной X, присваивая ранг 1 наименьшему значению, и т.д. Занести ранги в первый столбец таблицы по порядку номеров испытуемых или признаков.
Проранжировать значения переменной У, в соответствии с теми же правилами. Занести ранги во второй столбец таблицы по порядку номеров испытуемых или признаков.
Подсчитать разности d между рангами X и Y по каждой строке таблицы и занести в третий столбец таблицы.
Возвести каждую разность в квадрат: d2. Эти значения занести в четвертый столбец таблицы.
Подсчитать сумму d2.
При наличии одинаковых рангов рассчитать поправки:
где a - объем каждой группы одинаковых рангов в
ранговом ряду X; b - объем каждой группы одинаковых
рангов в ранговом ряду Y.

Лекция по стат моделированию № 5, Лакман И.А.

отсутствии одинаковых рангов

при наличии одинаковых рангов
где sum(d2) -

сумма квадратов разностей между рангами; Ta и Tb - поправки на одинаковые ранги; N - количество наблюдений признаков, участвовавших в ранжировании.

Схема нахождения коэффициента Корреляции Спирмена

Лекция по стат моделированию № 5, Лакман И.А.

вид:
Н0: коэффициент ранговой корреляции Спирмена rs незначимый;
Н1: коэффициент ранговой корреляции

Спирмена rs значим.
Расcчитывается t-статистика по формуле:




Определяется tтабл по таблице Стьюдента со степенями свободы n-2 и уровнем значимости α
Если , то Н0 отклоняют на заданном уровне значимости, и считаем, что коэффициент ранговой корреляции Спирмена значимый.

Лекция по стат моделированию № 5, Лакман И.А.

выстраивают сопряженные наблюдения пар (хi , yi) и записывают их

в таблицу.
2. Для каждого значения yi определяют его ранг si, записывается в таблицу.
3. На последовательности рангов s1, s2, …, sN определяют количество инверсий, т.е. нарушений порядка следования. Например, при N = 4 и последовательности рангов {1, 3, 4, 2} имеем количество инверсий: 3 – количество инверсий для числа 1 (после числа 1 есть три значения, больше 1) и 1 – количество инверсий для числа 3 (после числа 3 есть одно значение, больше 3).
4. Формируют ряд значений в таблице из инверсий, если инверсий нет, то присваивают ячейке значение 0.
5. Рассчитывают сумму всех инверсий К:
6. Определяют коэффициент ранговой корреляции по Кендаллу:

Лекция по стат моделированию № 5, Лакман И.А.

Кендалла, то есть для проверки существенности корреляционной связи, выдвигают гипотезы:
Н0:

коэффициент ранговой корреляции Кендалла τК незначимый (τК=0);
Н1: коэффициент ранговой корреляции Кендалла τК значим (τК ≠0);.
Рассчитывается Z-статистика по формуле:

По таблице значений функции Лапласа определяем zтабл из равенства для
уровня значимости α.

Примечание: zтабл можно определить также в модуле Вероятностный калькулятор, выбрав нормальное распределение Z, р=1–α , mean=0, st.dev=1, и отметив режим двусторонней проверки гипотезы.
Если , следовательно, нулевую гипотезу о незначимости коэффициента Кендалла (τК=0), можно отклонить на заданном уровне значимости α.

Лекция по стат моделированию № 5, Лакман И.А.

тесноту связи между несколькими ранжированными признаками, называется коэффициентом конкордации.
Определить, какие

признаки будут участвовать в сопоставлении как переменные (X, Y, Z,…).
Проранжировать значения всех признаков, присваивая ранг 1 наименьшему значению, и т.д. Занести ранги в столбцы таблицы по порядку номеров признаков (Rx, Ry, Rz,…).
Сформировать в таблице столбец из суммы всех рангов (Rs=Rx+Ry+Rz+…).
Сформировать в таблице столбец из квадратов сумм всех рангов, полученных в п.3. Rs2
Определить по столбцу из сумм всех рангов (полученных в п.3) среднее значение, где n – число наблюдений.

Лекция по стат моделированию № 5, Лакман И.А.

средне квадратов рангов.

7. Вычислить коэффициент конкордации:
Где m- количество факторов (признаков

сравнения),
n – число наблюдений.
Для проверки значимости коэффициента конкордации, выдвигают гипотезы:
Н0: коэффициент конкордации W незначимый (W=0);
Н1: коэффициент конкордации W значим (W ≠0);.
Рассчитывается χ2-статистика по формуле:
По таблице значений χ2-распределения определяем χ2 табл , для степени свободы v=n и уровня значимости α.
Если χ2>χ2 табл следовательно, нулевую гипотезу о незначимости коэффициента конкордации (W=0), можно отклонить на заданном уровне значимости α.
Примечание, χ2 табл можно определить из модуля Вероятностный калькулятор пакета Statistica.

Лекция по стат моделированию № 5, Лакман И.А.

качественные признаки состоят только из двух групп, то для определения

тесноты связи двух качественных признаков применяют коэффициенты ассоциации и контингенции.
Схема нахождения коэффициентов
1. Пусть I явление имеет две альтернативы a и b, причем частоты их появления соответственно: na и nb.
Пусть II явление имеет две альтернативы c и d, причем частоты их появления соответственно: nc и nd
2. Составляется таблица:

Лекция по стат моделированию № 5, Лакман И.А.

naс + nad. и nb. = nbс + nbd
nc =

naс + nbc. и nd. = nad + nbd
4. Определяется коэффициент ассоциации как:


Определяется коэффициент контингенции:



5. Связь считается подтвержденной если Ka>0,5, а Kk>0,3.
Примечание. Коэффициент контингенции всегда меньше коэффициента ассоциации.

Лекция по стат моделированию № 5, Лакман И.А.

групп, то для определения тесноты связи качественных признаков применяют коэффициенты

сопряженности Пирсона и Чупрова.
Схема нахождения коэффициентов сопряженности
1. Пусть I явление имеет альтернативы aI, bI, cI и т.д., причем частоты их появления соответственно: naI , nbI. ncI …
Пусть II явление имеет альтернативы aII, bII, cII и т.д, причем частоты их появления соответственно: naII , nbII. ncII …
2. Составляется таблица:

Лекция по стат моделированию № 5, Лакман И.А.

+ nbI,aII + ncI,aII ; nbII = naI,bII + nbI,bII

+ ncI,bII
ncII = naI,cII + nbI,cII + ncI,cII
И naI = naI,aII + naI,bII + naI,cII ; nbI = nbI,aII + nbI,bII + nbI,cII
ncI = ncI,aII + ncI,bII + ncI,cII
4. Определяется значение:

Лекция по стат моделированию № 5, Лакман И.А.

Пирсона:


6. Определяется коэффициент взаимной сопряженности Чупрова:



Где К1 – число значений

(групп) I-ого признака.
Где К2 – число значений (групп) II-ого признака.

Чем ближе коэффициенты взаимной сопряженности к единице, тем теснее связь.

Лекция по стат моделированию № 5, Лакман И.А.

признака определяют на основе биссериального коэффициента корреляции.
Схема нахождения коэффициентов сопряженности
1.Пусть

даны два качественных признака (категории или группы), для которых известны количественные характеристики. Количество наблюдений в I-ой группе – n1, в II-ой группе – n2. Общее количество наблюдений n= n1 + n2.
2. По каждому из признаков (группе) определяется среднее значение: и

3. Определяются доли каждой группы в общем объеме:
Для I –ой группы: p= n1/n
Для II-ой группы: q= n2/n
4. Рассчитывается общее среднее значение для обеих групп (признаков)

Лекция по стат моделированию № 5, Лакман И.А.

от среднего уровня:


6. По таблице значений функции Лапласа определяем zтабл

из равенства для уровня значимости α.

7. Определяется биссериальный коэффициент корреляции:



Чем ближе значение коэффициента к единице, тем теснее связь между признаками.

Лекция по стат моделированию № 5, Лакман И.А.