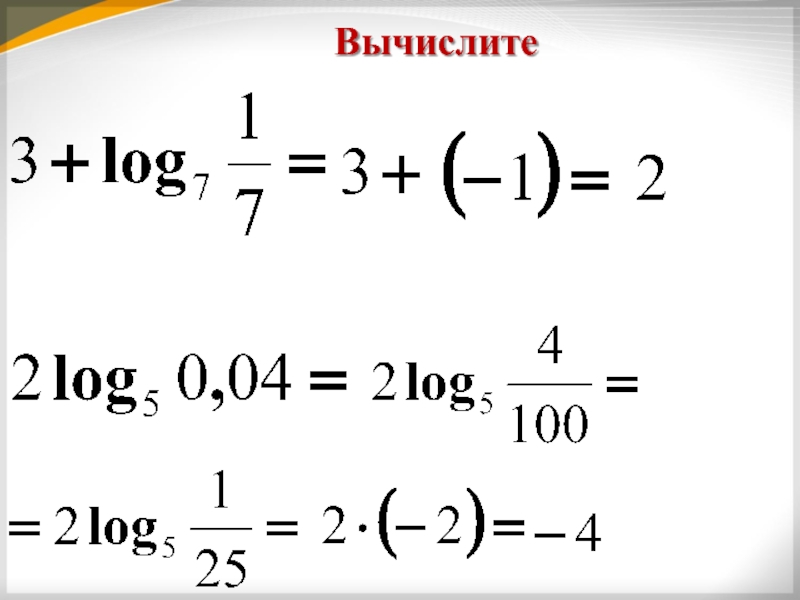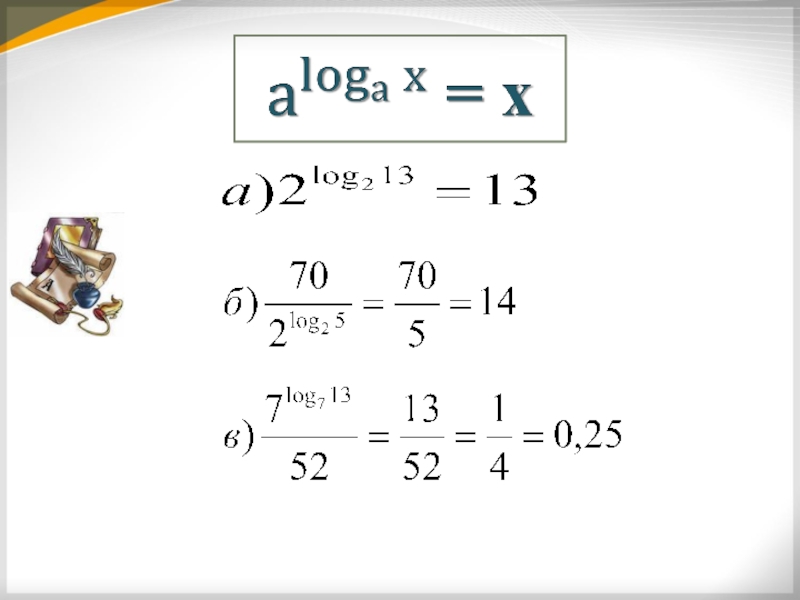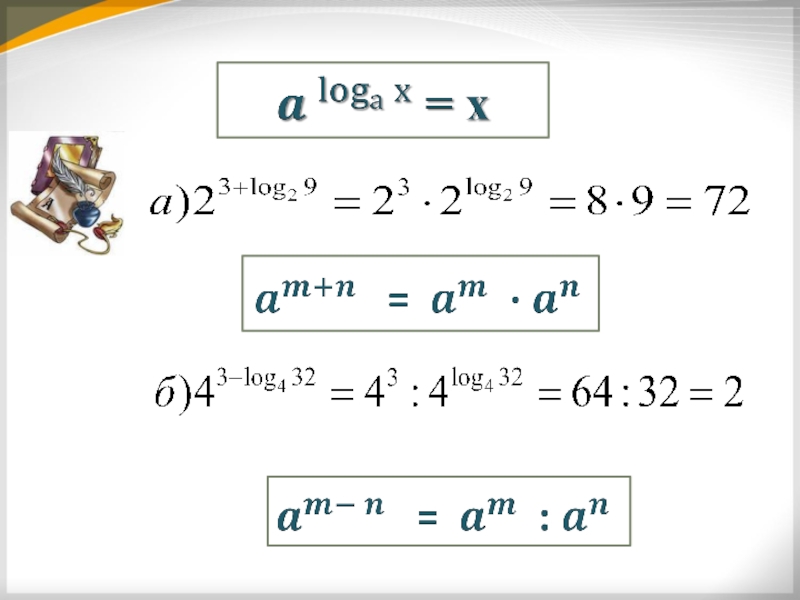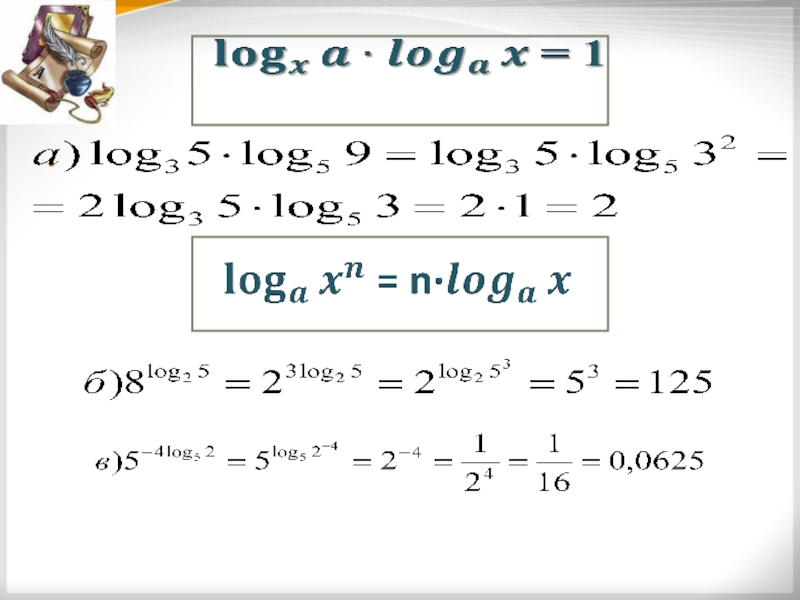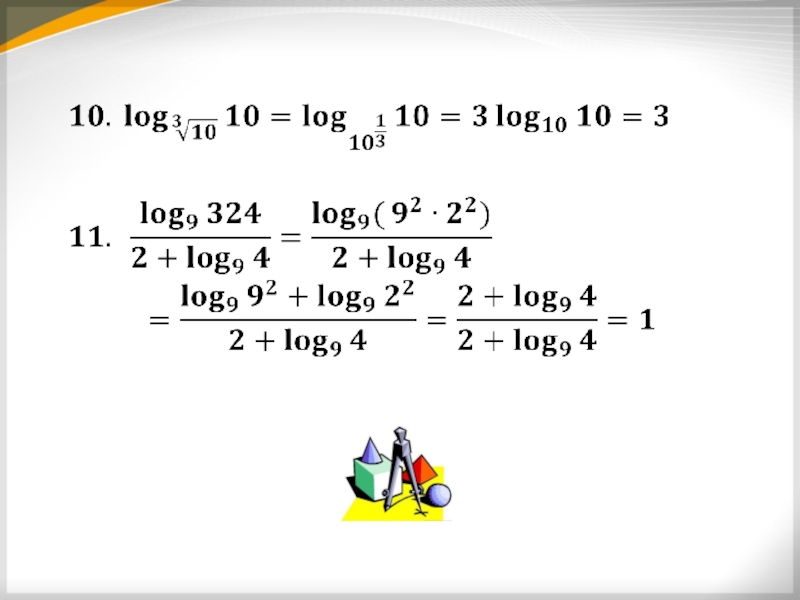Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПОНЯТИЕ ЛОГАРИФМА
Содержание
- 1. ПОНЯТИЕ ЛОГАРИФМА
- 2. Определение логарифмаЛогарифмом числа b по основанию
- 3. b >0a>0, a≠1b = acс = loga
- 4. При каких значениях х существует логарифм
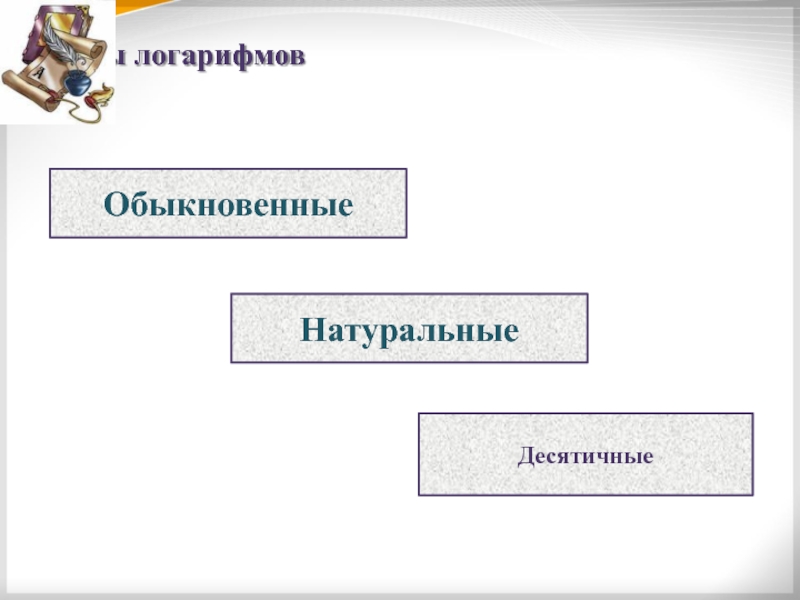
- 5. Виды логарифмовДесятичныеОбыкновенныеНатуральные
- 6. Примеры
- 7. Запишите в виде логарифмического равенства:(по определению);(по определению);
- 8. Найдите число x
- 9. Найдите число x
- 10. Вычислите
- 11. Вычислите
- 12. Особые логарифмы
- 13. Пример
- 14. Свойства десятичных логарифмов:
- 15. Пример
- 16. Слайд 16
- 17. Найдите число х.
- 18. Свойства логарифмов
- 19. ОСНОВНОЕ ЛОГАРИФМИЧЕСКОЕ ТОЖДЕСТВО ( где b>0,a>0 и a ≠1)
- 20.
- 21. Свойства логарифмов
- 22. Вычислите:6Решение
- 23. Вычислите:0Решение
- 24. Вычислите:1Решение
- 25. Вычислите:40Решение
- 26.
- 27. Вычислите:
- 28.
- 29. Свойства логарифмов
- 30. 1. Логарифм произведения равен сумме логарифмов множителей
- 31. Свойства логарифмов т. е.
- 32. Вычислите:2Решение
- 33. Вычислите:log18 2 + log18 9log4 8 +
- 34. 2. Логарифм частного равен логарифмов делимого без логарифма делителя
- 35. Свойства логарифмов
- 36. Вычислите:– 1Решение
- 37. Вычислите:– 2Решение
- 38. Вычислите:6Решениев ы х о д
- 39. 3. Логарифм степени равен произведению показателя степени на логарифм ее основания
- 40. 4. Логарифм, у которого основание в степени
- 41. Формула перехода к новому основанию:Из этой формулы следует равенство:
- 42. Вычислите:2Решение
- 43. Свойства логарифмов
- 44.
- 45. Вычислите:3 4 16 0,01
- 46. Примеры
- 47. Вычислите:12 3 2 0,5
- 48. Преобразование логарифмических выражений
- 49. Преобразование логарифмических выражений
- 50.
- 51.
- 52. Справочная информация.
- 53. Скачать презентанцию
Определение логарифмаЛогарифмом числа b по основанию а называется показатель степени, в которую нужно возвести а, чтобы получить b.