Последовательный колебательный контур. Основные понятия и определения. Частотные характеристики последовательного колебательно

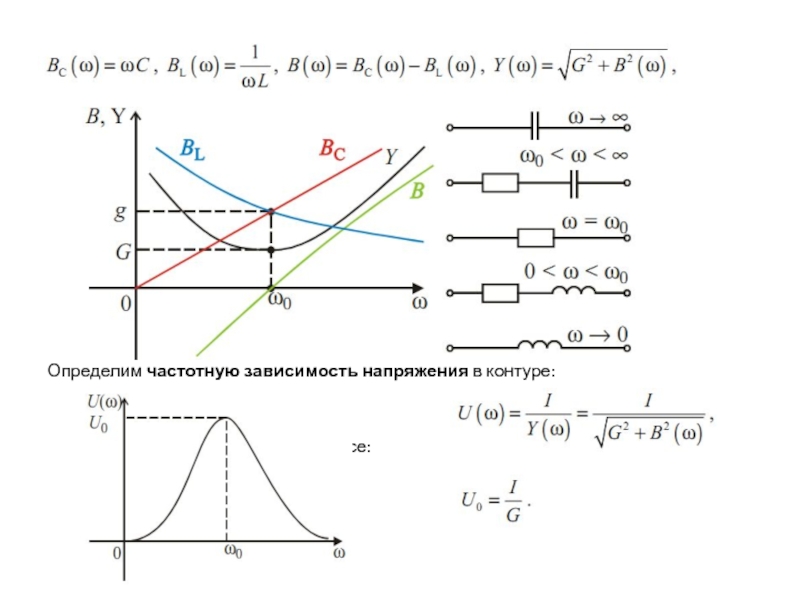
колебательного контура. Параллельный колебательный контур. Основные понятия и определения. Частотные характеристики

параллельного колебательного контура. Методика расчета резонансной частоты колебательных контуров.

Последовательный колебательный контур. Основные понятия и определения.
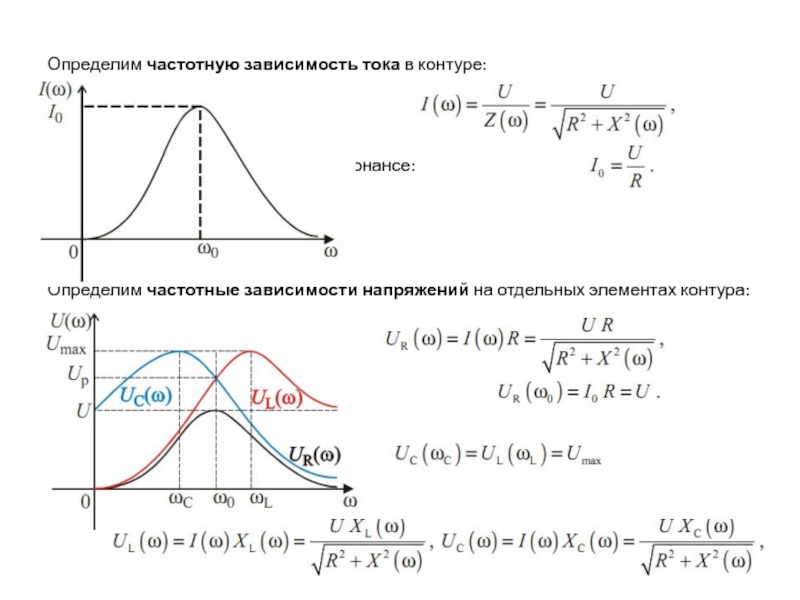
Имеет место резонанс напряжений.
Резонансная частота:


Резистивное сопротивление контура при резонансе.


Определим реактивные сопротивления на индуктивности и емкости при резонансе:


Видно, что сопротивления
характеристическое сопротивление контура.

запасенной в контуре при резонансе;
активная энергия, поглощаемая в контуре за период затухание.
Для выяснения физического смысла параметра исследуем энергетические соотношения в контуре при резонансе. Обозначим резонансный ток как
В контуре происходит периодический обмен энергии электрического и магнитного полей, то есть

Значение активной энергии, рассеиваемой в контуре, определяется как:


В итоге получаем формулу добротностьи:

раз резонансные напряжения на
реактивных элементах превышают приложенное напряжение.
Величины

являются первичными параметрами контура.
Величины являются вторичными параметрами контура.
Частотные характеристики последовательного колебательного контура.
Из-за наличия в контуре реактивных элементов, видно:

напряжений на отдельных элементах контура:


при резонансе:

дуальности позволяет распространить частотные характеристики
последовательного колебательного контура на частотные

характеристики параллельного контура. В параллельном колебательном контуре имеет место резонанс токов с частотой:





При резонансе:


где g – характеристическая проводимость контура.
Добротность определяется как:

при резонансе: откуда определим добротность:



Методика расчёта резонансной частоты

колебательных контуров
Определим эквивалентное сопротивление цепи:

при резонансе:


Таким образом, после алгебраических
упрощений получим уравнение: