Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Построение графиков функций содержащих знак модуля для учащихся гуманитарного
Содержание
- 1. Построение графиков функций содержащих знак модуля для учащихся гуманитарного
- 2. График функции у = |х|
- 3. График функции у = - |х|Получается симметричным
- 4. График функции у=|х|+а получается параллельным переносом
- 5. График функции у=а|х| получается растяжением графика у=|х|
- 6. График функции у = |x+a| получается параллельнымпереносом
- 7. Построить график функции у = х² -
- 8. Слайд 8
- 9. 2 способ. Если рассмотрим
- 10. Для построения графика функции у = |f(х)
- 11. Построить график функции у = |х² -
- 12. Построить график функции у = |х +
- 13. у = |х + 3| + |2x
- 14. 3. При
- 15. Слайд 15
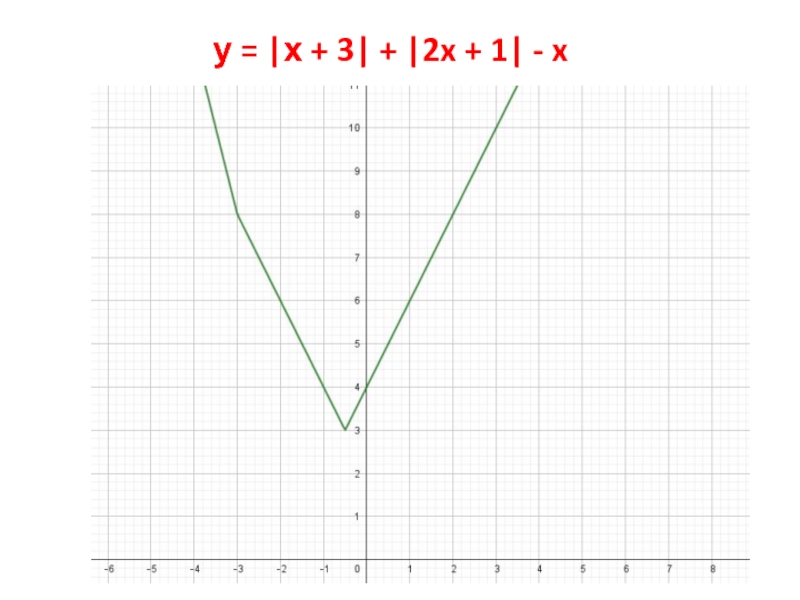
- 16. у = |х + 3| + |2x + 1| - x
- 17. Построить график функции у =
- 18. у = |
- 19. у = | х²
- 20. Найти корни уравнения ||x-2|-5| = 3. Выполняем построение первого
- 21. Найти корни уравнения ||x-2|-5|=3. Нетрудно определить по графику, что
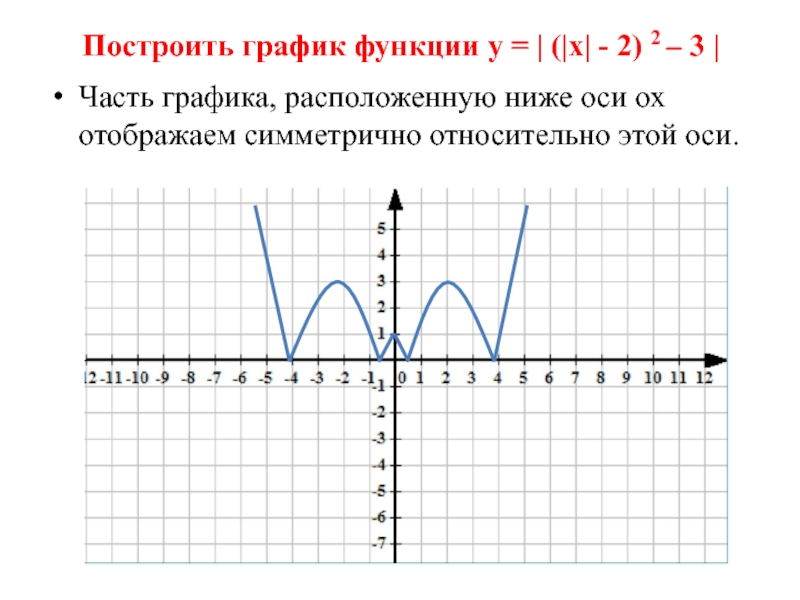
- 22. Построить график функции у = | (|х|
- 23. Построить график функции у = | (|х|
- 24. Построить график функции у = | (|х|
- 25. График неравенства | у - 2х
- 26. Выводы: Для построения графика функции
- 27. у = f |(х)|у =| f (х)|у = |f |(х)||у = f(х), х>0Построить часть для х
- 28. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Построение графиков функций содержащих знак модуля для учащихся гуманитарного класса.
Учитель
математики
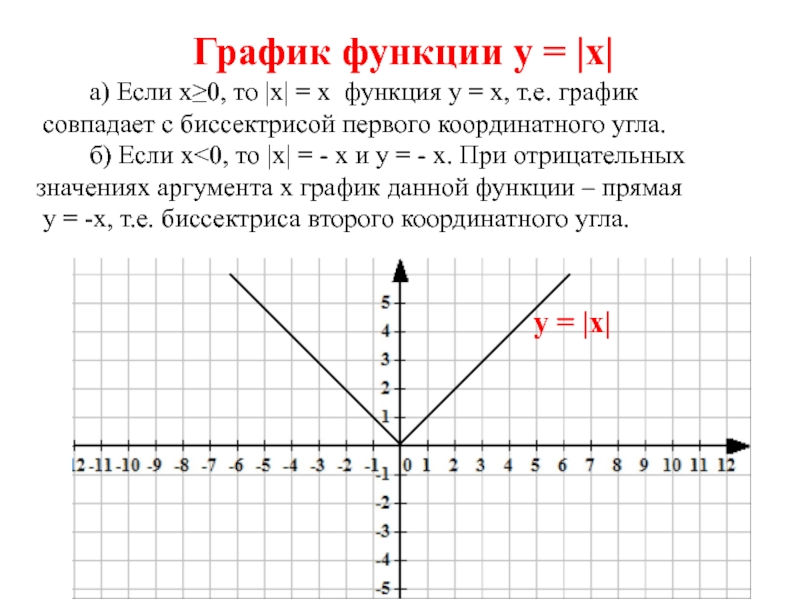
Слайд 2График функции у = |х|
а) Если
х≥0, то |х| = х функция у = х, т.е.
графиксовпадает с биссектрисой первого координатного угла.
б) Если х<0, то |х| = - х и у = - х. При отрицательных
значениях аргумента х график данной функции – прямая
у = -х, т.е. биссектриса второго координатного угла.
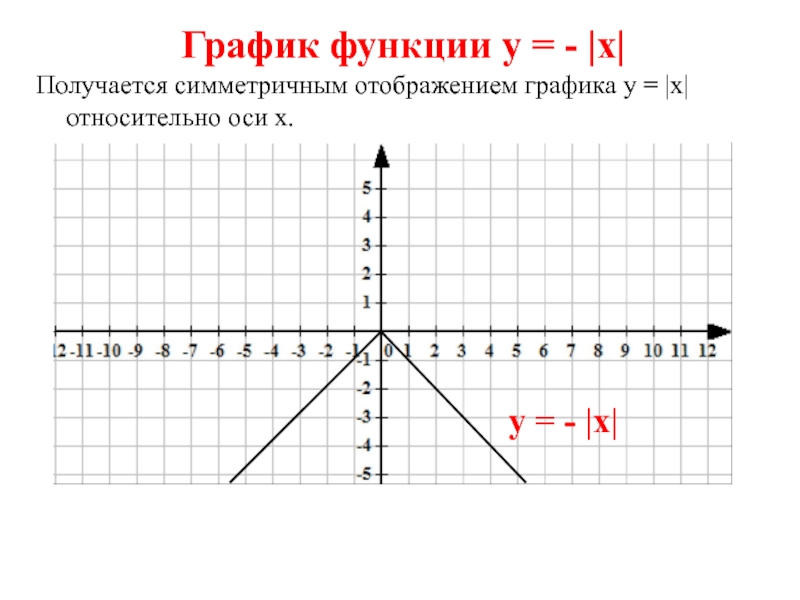
Слайд 3График функции у = - |х|
Получается симметричным отображением графика у
= |х| относительно оси х.
у =
- |х|Слайд 4График функции у=|х|+а получается параллельным переносом графика у=|х|
в положительном направлении оси у на а единиц отрезка
при а>0 и в отрицательном направлении на а единиц при а<0.График функции у = |х| + а
у = |х| + а
у = |х| - а
у = |х|
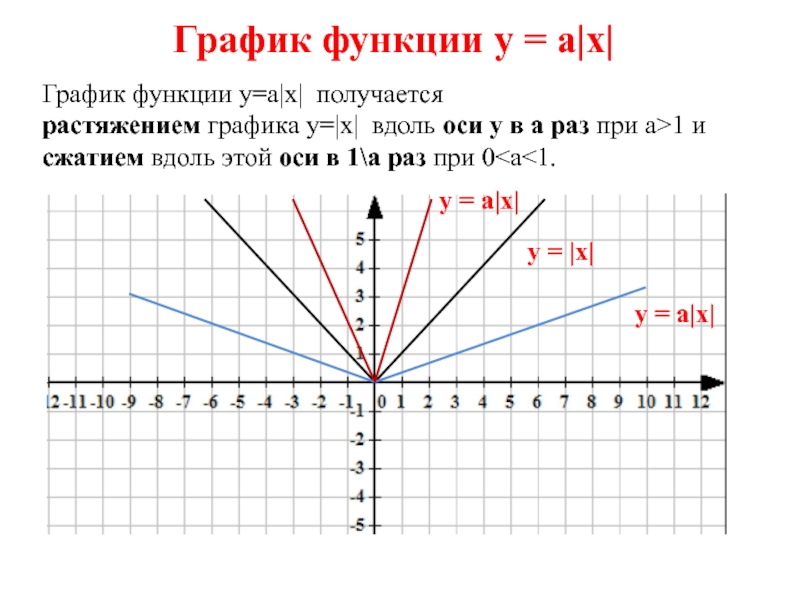
Слайд 5График функции у=а|х| получается
растяжением графика у=|х| вдоль оси у
в а раз при а>1 и
сжатием вдоль этой оси
в 1\а раз при 0График функции у = а|х|
у = а|х|
у = а|х|
у = |х|
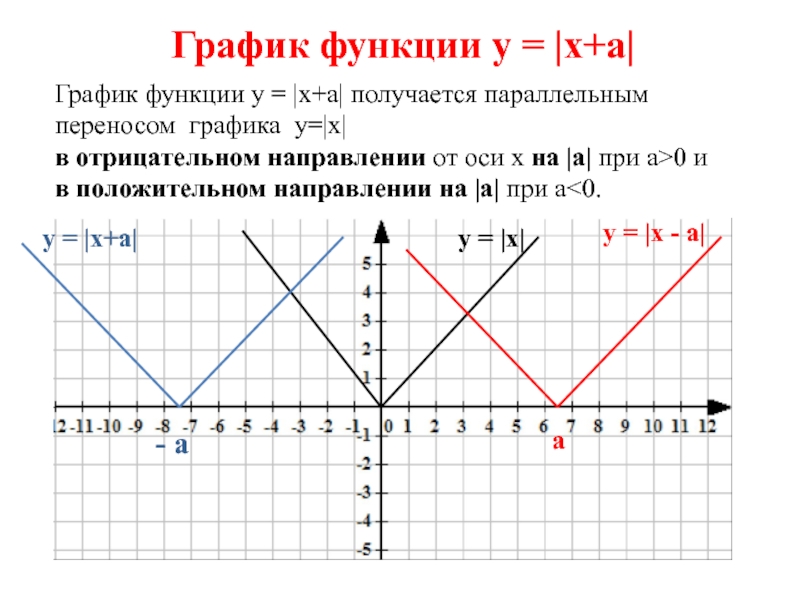
Слайд 6График функции у = |x+a| получается параллельным
переносом графика y=|x|
в
отрицательном направлении от оси х на |а| при а>0 и
в положительном направлении на |a| при a<0.
График функции у = |х+а|
- а
а
у = |х+а|
у = |х - а|
у = |х|
Слайд 7
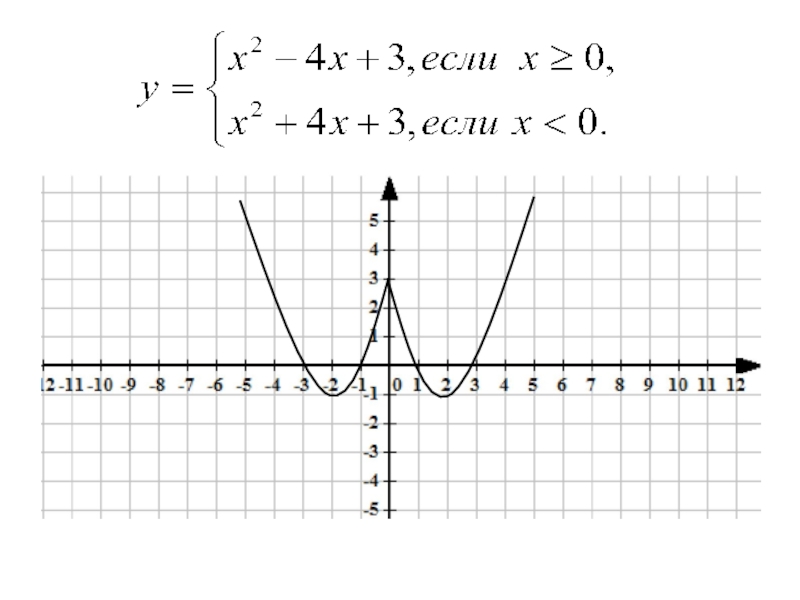
Построить график функции у = х² - 4|х| + 3.
1 способ.
Раскрываем |х| = х при х≥0, получаем график
у = х² - 4х + 3. При х<0, |х|= - х, получаем график у = х² + 4х + 3.
Строим кусочно – заданную функцию по алгоритму:
Находим вершину параболы для каждой функции.
Находим точки пересечения каждой параболы с осью х.
Строим параболы по заданным условиям.
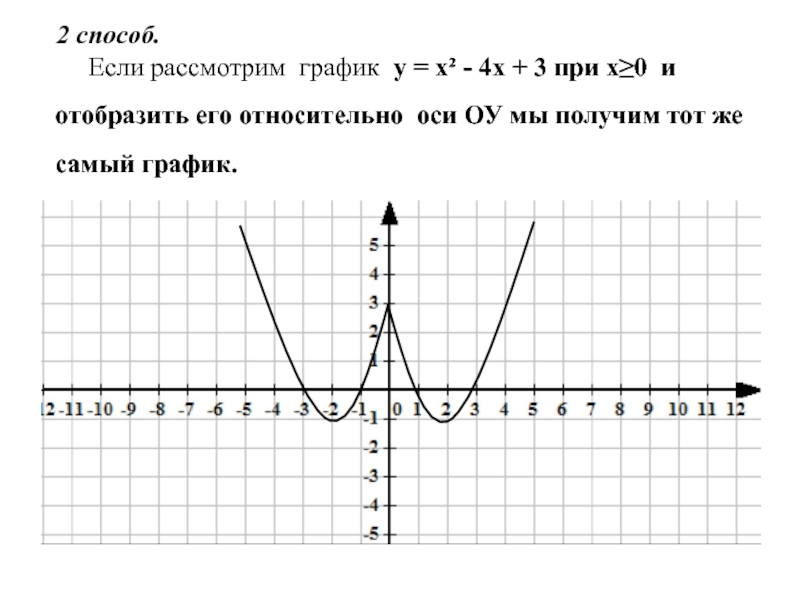
Слайд 9 2 способ.
Если рассмотрим график у =
х² - 4х + 3 при х≥0 и
отобразить
его относительно оси ОУ мы получим тот жесамый график.
Слайд 10Для построения графика функции у = |f(х) | достаточно:
1.Построить график
функции у = f(х) ;
2. На участках, где график расположен
в нижней полуплоскости, т.е., где f(х) <0, симметрично отражаем относительно оси абсцисс.
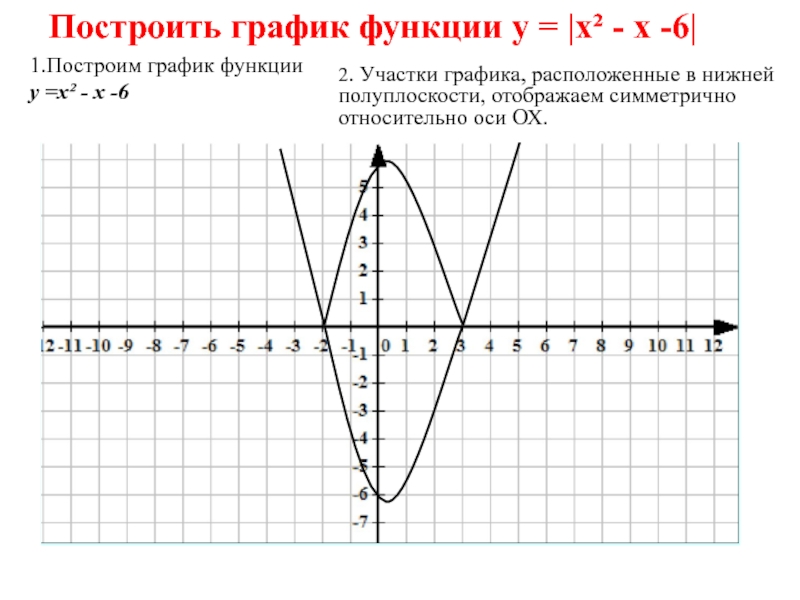
Слайд 11Построить график функции у = |х² - х -6|
1.Построим график
функции
у =х² - х -6
2. Участки графика, расположенные в
нижней полуплоскости, отображаем симметрично относительно оси ОХ. Слайд 12Построить график функции у = |х + 3| + |2x
+ 1| - x
Строить график будем с помощью раскрытия модуля.
Алгоритм
построения:Приравняем каждое подмодульное выражение к нулю и находим точки, в которых подмодульные выражения, входящие в уравнение функции меняют знак.
Наносим эти точки на ось х и выделяем промежутки, в которых подмодульные выражения сохраняют знак.
Раскрываем модуль на каждом промежутке и получаем соответствующие уравнения функции.
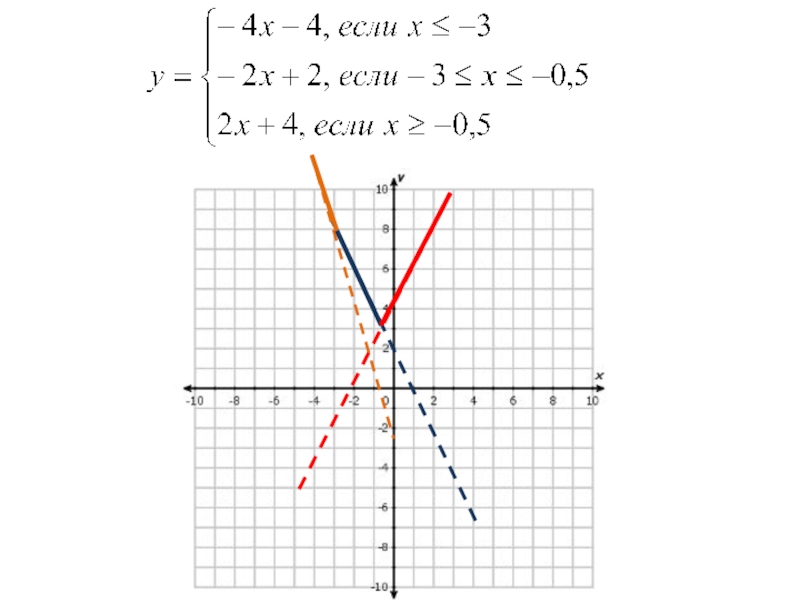
Строим график на каждом промежутке.
Слайд 13у = |х + 3| + |2x + 1| -
x
Приравниваем каждое подмодульное выражение к нулю и находим точки, в
которых происходит смена знака:Наносим точки на ось х:
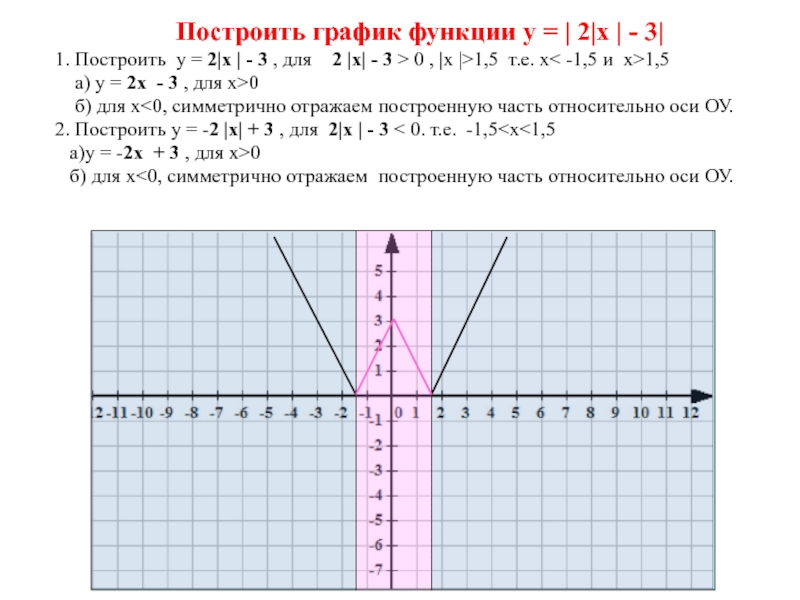
Слайд 17 Построить график функции у = | 2|х |
- 3|
1. Построить у = 2|х | - 3 ,
для 2 |х| - 3 > 0 , |х |>1,5 т.е. х< -1,5 и х>1,5а) у = 2х - 3 , для х>0
б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.
2. Построить у = -2 |х| + 3 , для 2|х | - 3 < 0. т.е. -1,5<х<1,5
а)у = -2х + 3 , для х>0
б) для х<0, симметрично отражаем построенную часть относительно оси ОУ.
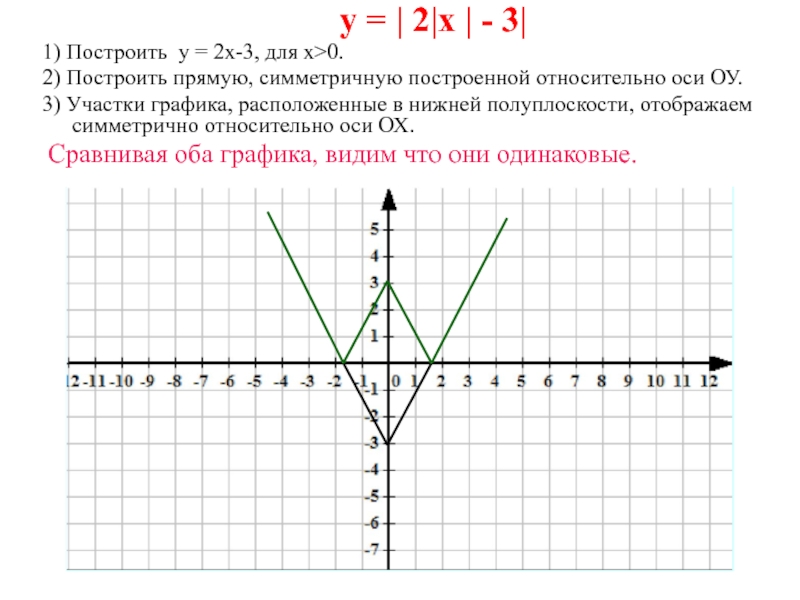
Слайд 18 у = | 2|х | -
3|
1) Построить у = 2х-3, для х>0.
2) Построить
прямую, симметричную построенной относительно оси ОУ.3) Участки графика, расположенные в нижней полуплоскости, отображаем симметрично относительно оси ОХ.
Сравнивая оба графика, видим что они одинаковые.
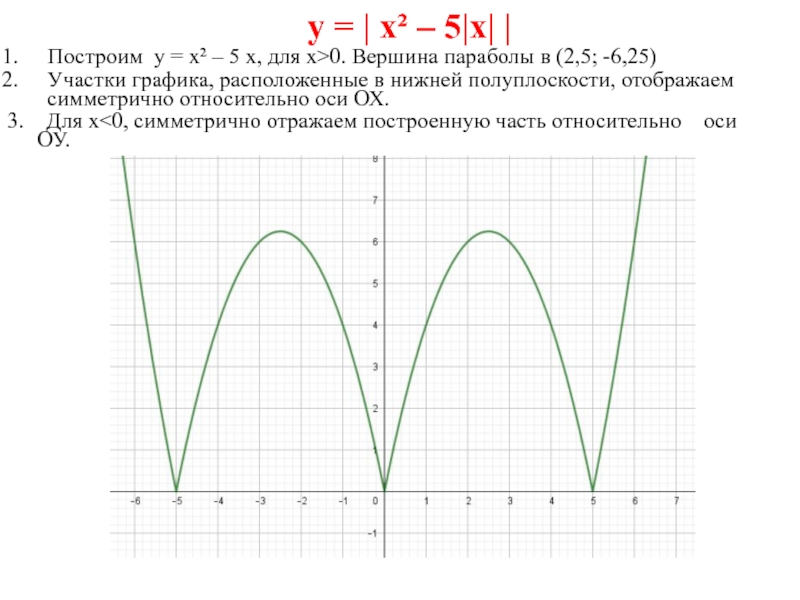
Слайд 19 у = | х² – 5|х| |
Построим
у = х² – 5 х, для х>0. Вершина параболы
в (2,5; -6,25)Участки графика, расположенные в нижней полуплоскости, отображаем симметрично относительно оси ОХ.
3. Для х<0, симметрично отражаем построенную часть относительно оси ОУ.
Слайд 20Найти корни уравнения ||x-2|-5| = 3.
Выполняем построение первого (внутреннего) модуля y
= |x-2|
Параллельно переносим линии вниз на 5, чтобы получить график функции y
= |x-2|- 5 Отражаем все что находится ниже оси абсцисс. Это и будет искомая функция y=||x-2|-5|. Также выполняем построение прямой у=3
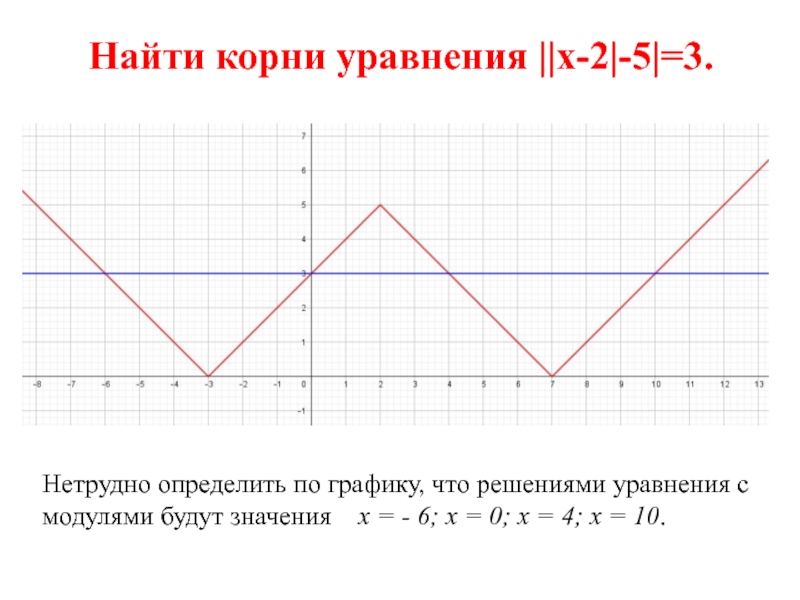
Слайд 21Найти корни уравнения ||x-2|-5|=3.
Нетрудно определить по графику, что решениями уравнения с
модулями будут значения x = - 6; x =
0; x = 4; x = 10.Слайд 22Построить график функции у = | (|х| - 2) 2
– 3 |
Строим график функции у = (х - 2)
2 – 3Совершаем преобразование: для этого часть графика, расположенную левее оси оу стираем.
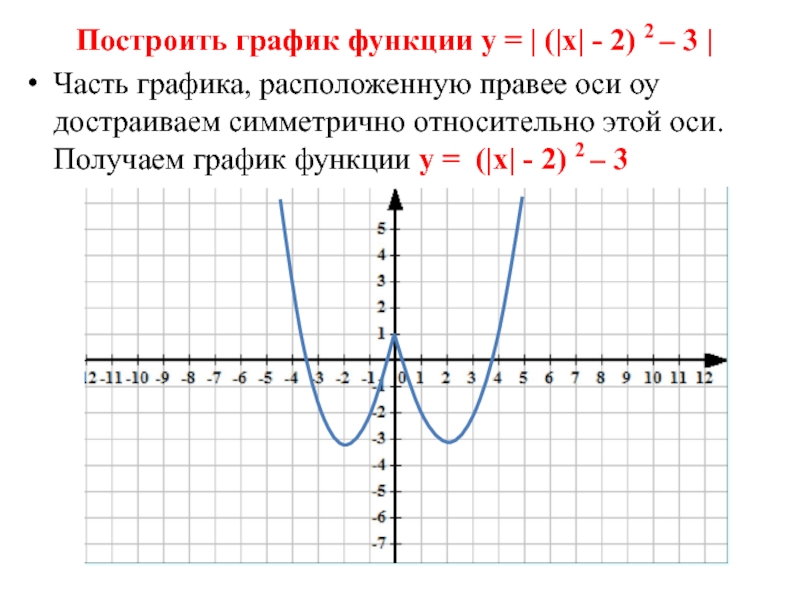
Слайд 23Построить график функции у = | (|х| - 2) 2
– 3 |
Часть графика, расположенную правее оси оу достраиваем симметрично
относительно этой оси. Получаем график функции у = (|х| - 2) 2 – 3 Слайд 24Построить график функции у = | (|х| - 2) 2
– 3 |
Часть графика, расположенную ниже оси ох отображаем симметрично
относительно этой оси.Слайд 25График неравенства | у - 2х -1| + 2|х|
≤ 3
Задача. Изобразите на координатной плоскости множество решений неравенства.
Раскроем модули.
Для этого каждое подмодульное выражение приравняем к нулю: у – 2х – 1 = 0; у = 2х + 1х = 0
Подмодульные выражения меняют знак при переходе через прямые у = 2х + 1 и х = 0.
Слайд 26Выводы:
Для построения графика функции у = f
|(х)|:
1.Построить график функции у = f(х) для
х>0;2.Построить для х<0 часть графика, симметричную построенной относительно оси ОУ.
Для построения графика функции у = | f(х) |
1.Построить график функции у = f(х) ;
2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, строить кривые, симметричные построенным графикам относительно оси абсцисс.
Для построения графика функции у = | f |(х)| |
1. Построить график функции у = f(х) для х>0.
2. Строим вторую часть графика, т. е. построенный график симметрично отражаем относительно ОУ
3. Участки получившегося графика, расположенные в нижней полуплоскости, преобразовываем на верхнюю полуплоскость симметрично оси ОХ.
Слайд 27у = f |(х)|
у =| f (х)|
у = |f |(х)||
у
= f(х), х>0
Построить часть для х
ОУу = f(х)
Часть графика, расположенного
в нижней полуплоскости
симметрично отобразить
относительно оси ОХ
Построить для х<0 часть
графика, симметричную
построенной относительно
оси ОУ
у = f(х), х>0






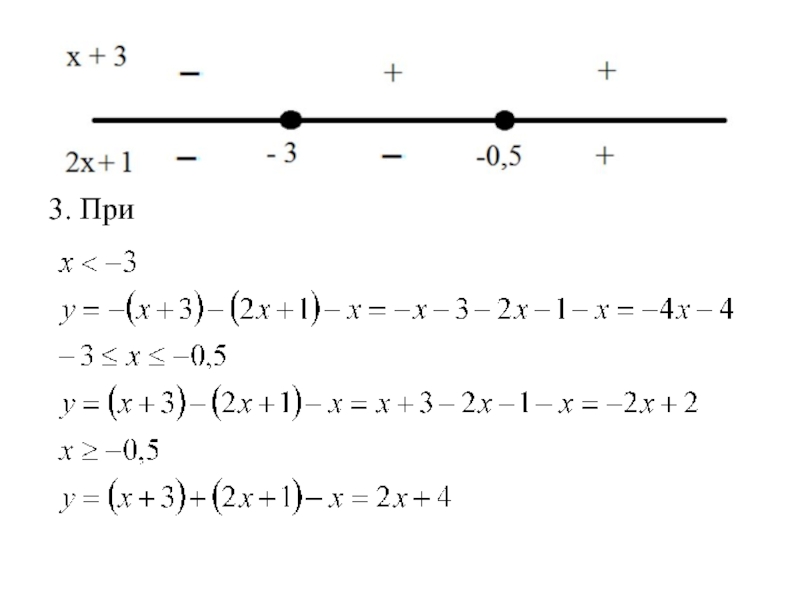














![АВТОМАТИЗАЦИЯ ЗВУКА [ Л ]
В СЛОВАХ](/img/tmb/6/598195/9904114927fd66f267234b3a5c44ea6c-800x.jpg)