Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ НА ОСНОВЕ АКСИОМАТИКИ
Содержание
- 1. ПОСТРОЕНИЕ СЕЧЕНИЙ МНОГОГРАННИКОВ НА ОСНОВЕ АКСИОМАТИКИ
- 2. Аксиомы стереометрии Аксиома 1.Через любые три точки,
- 3. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой плоскости.Аксиома 2:
- 4. Если две плоскости имеют общую точку, то
- 5. Следствия из аксиом стереометрии1. Через прямую и
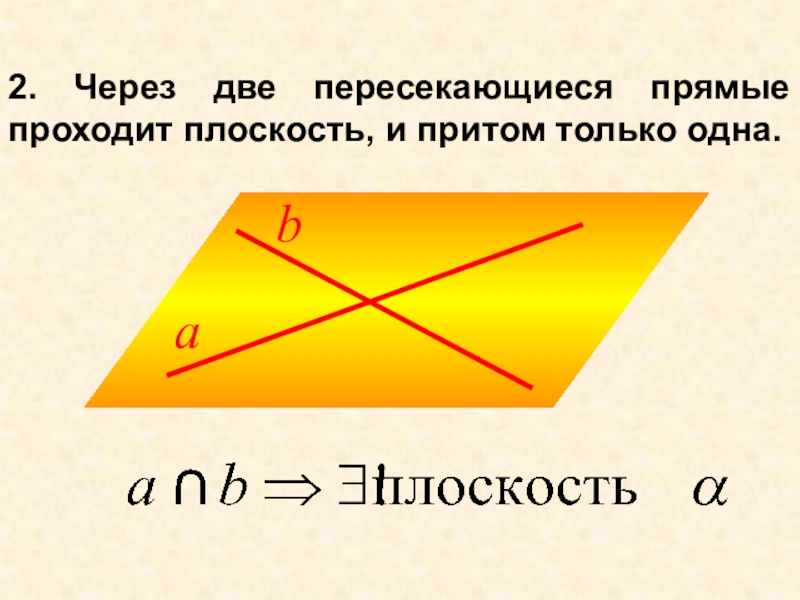
- 6. 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
- 7. Взаимное расположение в пространстве двух прямыхДве прямые
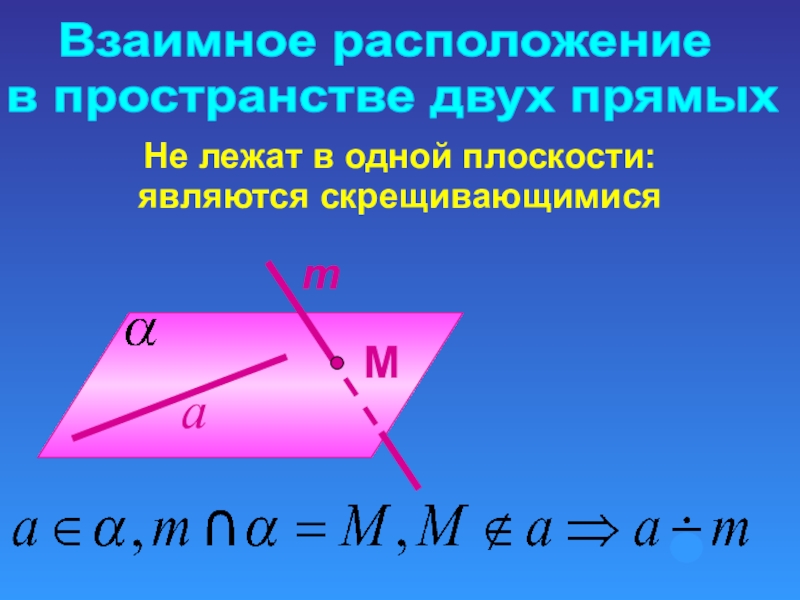
- 8. Взаимное расположение в пространстве двух прямыхНе лежат в одной плоскости: являются скрещивающимисяm
- 9. Взаимное расположение в пространстве прямой и плоскости1.
- 10. 3. Прямая параллельна плоскости.Если прямая, не лежащая
- 11. Способы задания плоскостейПо трем точкам (аксиома 1)По
- 12. Взаимное расположение плоскости и многогранникаВАНет точек пересеченияОдна точка пересеченияПересечением является отрезокПересечением является плоскость
- 13. Секущей плоскостью многогранника называют любую плоскость, по
- 14. Используя полученные знания, применим их к построению сечений многогранников на основе аксиоматики.ПРОБЛЕМА!!!
- 15. Алгоритм построения сеченияПостроить точки пересечения секущей плоскости
- 16. №1. Построить сечение, определенное точками K,
- 17. N2. Построить сечение, определяемое пересекающимися прямыми АС1
- 18. АА1В1С1D1DСN3. Определите вид сечения куба АВСДА1В1С1Д1 плоскостью,
- 19. АА1В1С1D1DВСN4. Постройте сечение куба плоскостью, проходящей через
- 20. N5. Построить сечение пирамиды плоскостью, проходящей через
- 21. МЕТОД СЛЕДОВСуть метода: построение вспомогательной прямой, являющейся
- 22. МРПостройте сечение куба, проходящее через точки P,
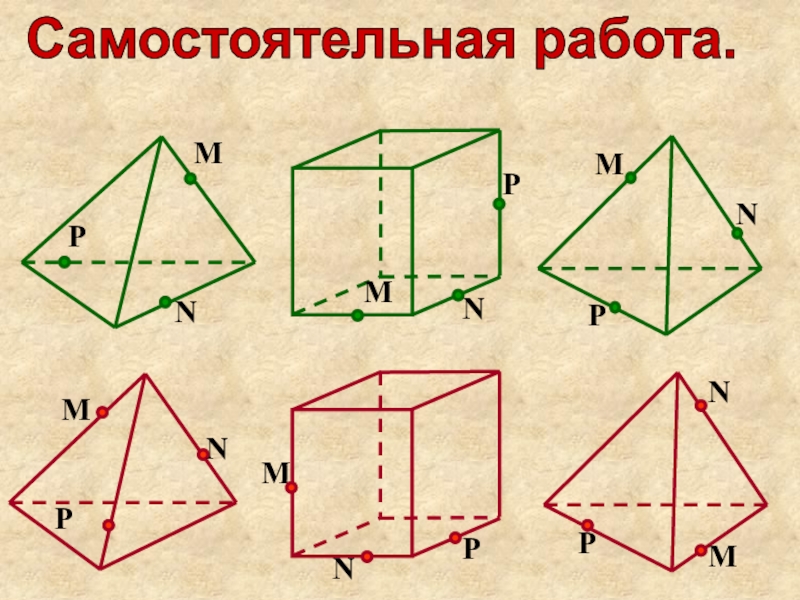
- 23. Самостоятельная работа.
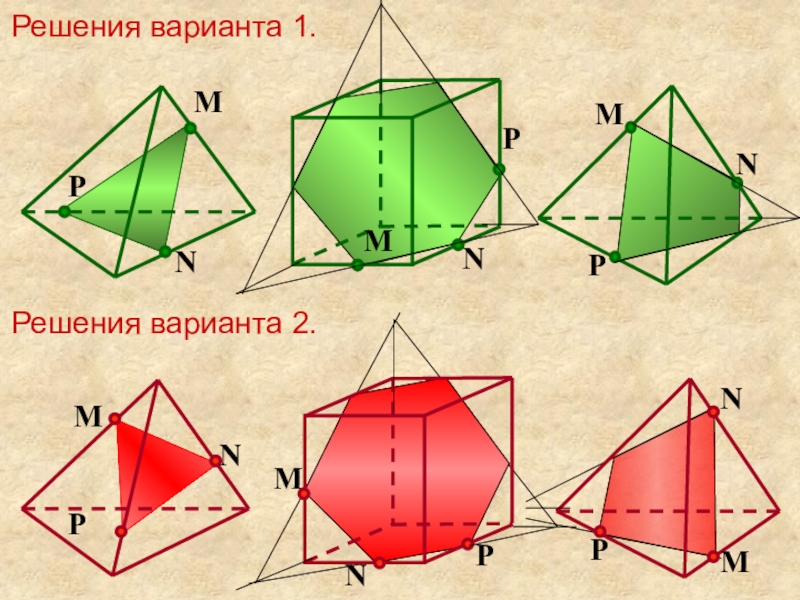
- 24. MNPMNPMNPРешения варианта 1.Решения варианта 2.MNPMNPMNP
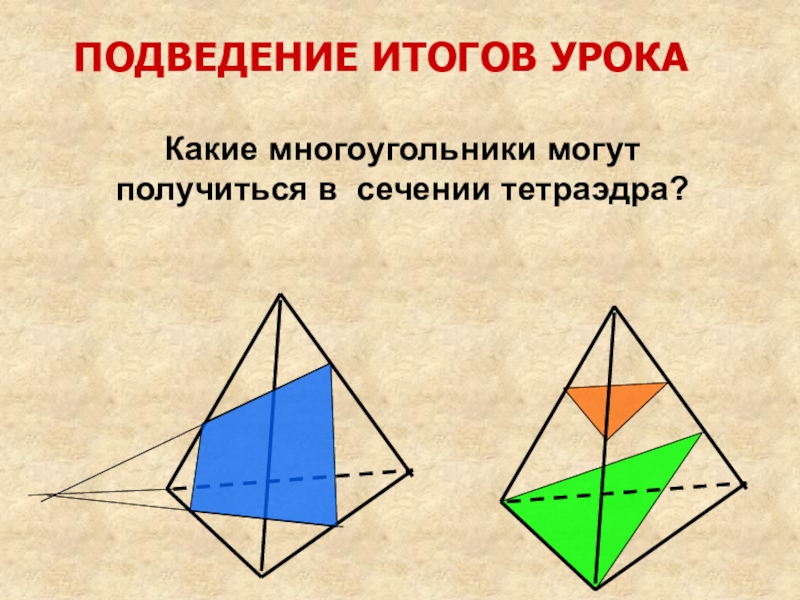
- 25. ПОДВЕДЕНИЕ ИТОГОВ УРОКАКакие многоугольники могут получиться в сечении тетраэдра?
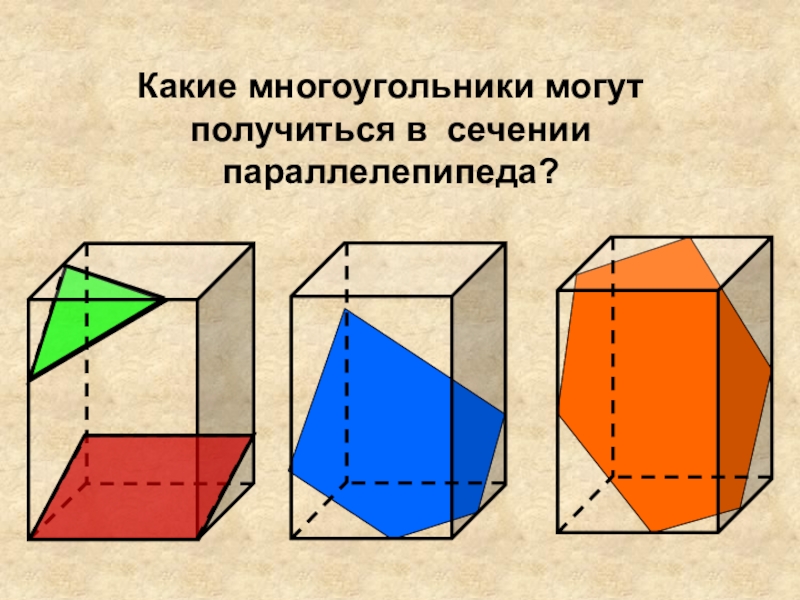
- 26. Какие многоугольники могут получиться в сечении параллелепипеда?
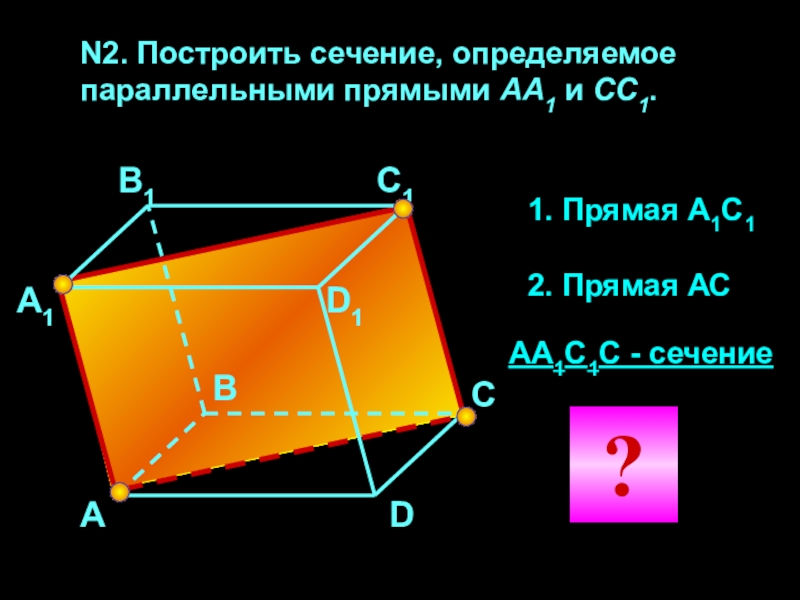
- 27. N2. Построить сечение, определяемое параллельными прямыми АА1 и CC1. АА1В1С1D1СВD1. Прямая А1С12. Прямая АСАА1С1С - сечение?
- 28. N4. Построить сечение по прямой BC и
- 29. N7. Построить сечение правильной призмы плоскостью, проходящей
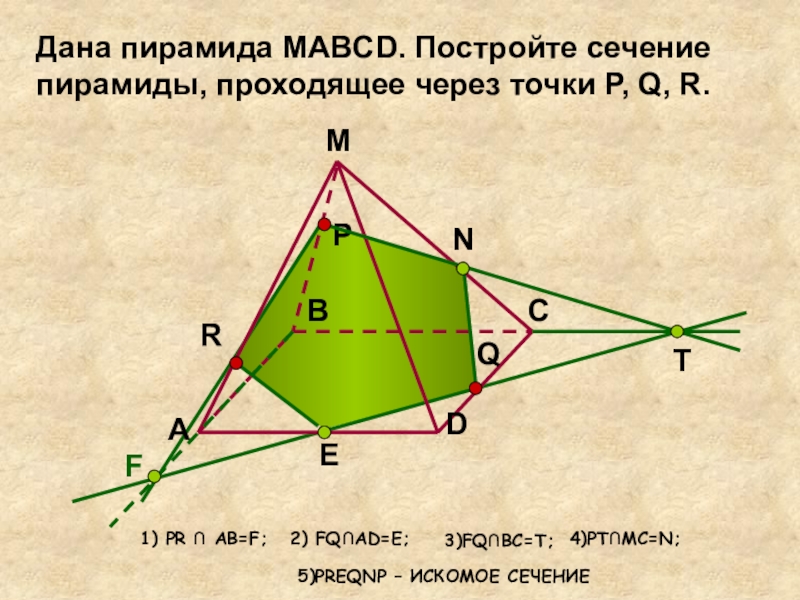
- 30. Дана пирамида MABCD. Постройте сечение пирамиды, проходящее
- 31. Скачать презентанцию
Аксиомы стереометрии Аксиома 1.Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом только одна.
Слайды и текст этой презентации
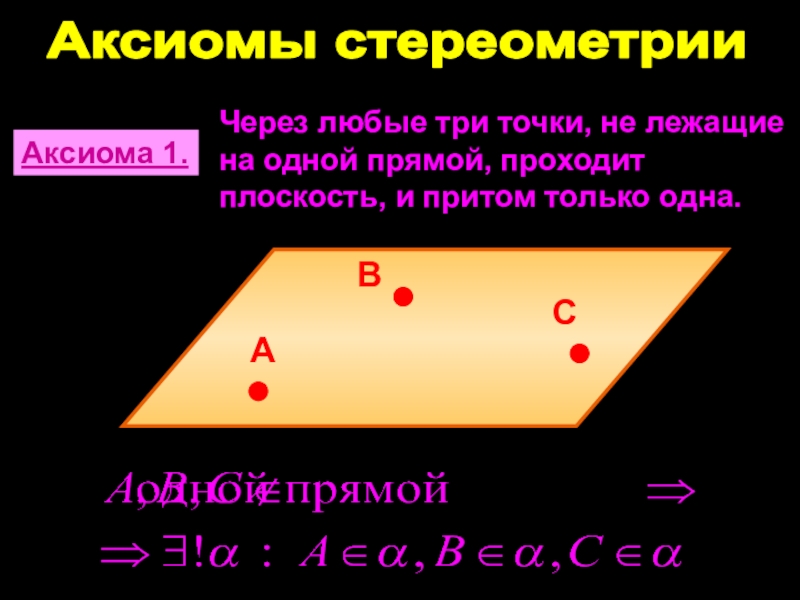
Слайд 2Аксиомы стереометрии
Аксиома 1.
Через любые три точки, не лежащие на
одной прямой, проходит плоскость, и притом только одна.
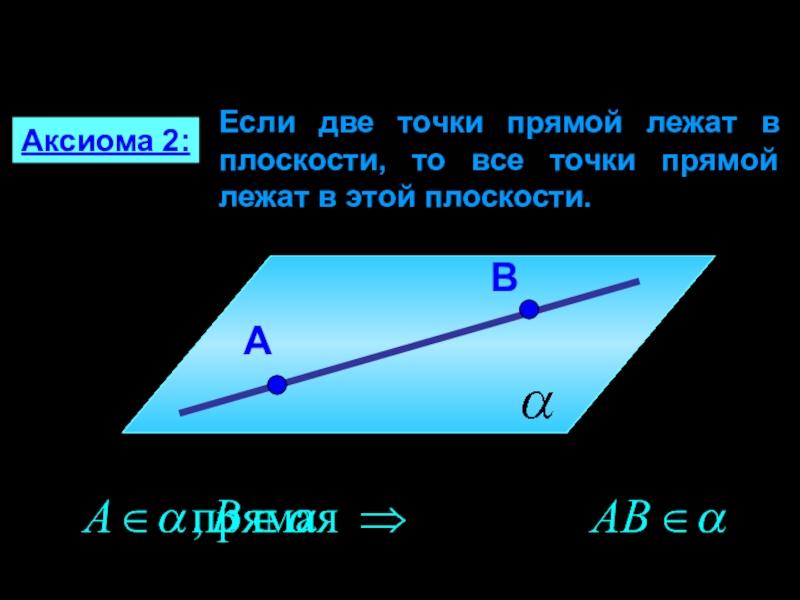
Слайд 3Если две точки прямой лежат в плоскости, то все точки
прямой лежат в этой плоскости.
Аксиома 2:
Слайд 4Если две плоскости имеют общую точку, то они имеют общую
прямую, на которой лежат все общие точки этих плоскостей.
Аксиома 3:
В таком случае говорят, что плоскости пересекаются по прямой
Слайд 5Следствия
из аксиом стереометрии
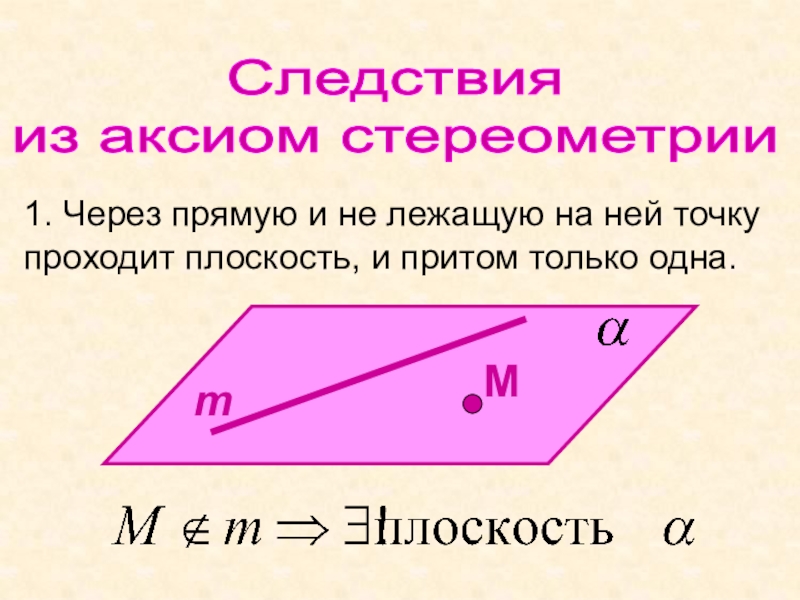
1. Через прямую и не лежащую на
ней точку проходит плоскость, и притом только одна.
Слайд 7Взаимное расположение
в пространстве двух прямых
Две прямые лежат в одной
плоскости
2. Прямые
пересекаются
1. Прямые
параллельны
Одна общая точка
Нет общих точек
Слайд 8Взаимное расположение
в пространстве двух прямых
Не лежат в одной плоскости:
являются скрещивающимися
m
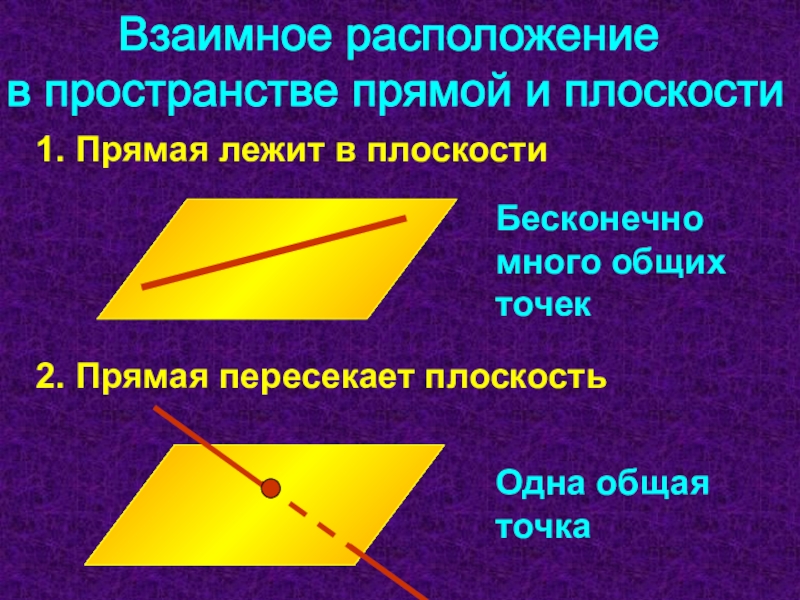
Слайд 9Взаимное расположение
в пространстве прямой и плоскости
1. Прямая лежит в
плоскости
2. Прямая пересекает плоскость
Бесконечно много общих точек
Одна общая точка
Слайд 103. Прямая параллельна плоскости.
Если прямая, не лежащая в данной плоскости,
параллельна какой-нибудь прямой, лежащей в этой плоскости, то она параллельна
данной плоскости.Нет общих точек
Признак параллельности прямой и плоскости:
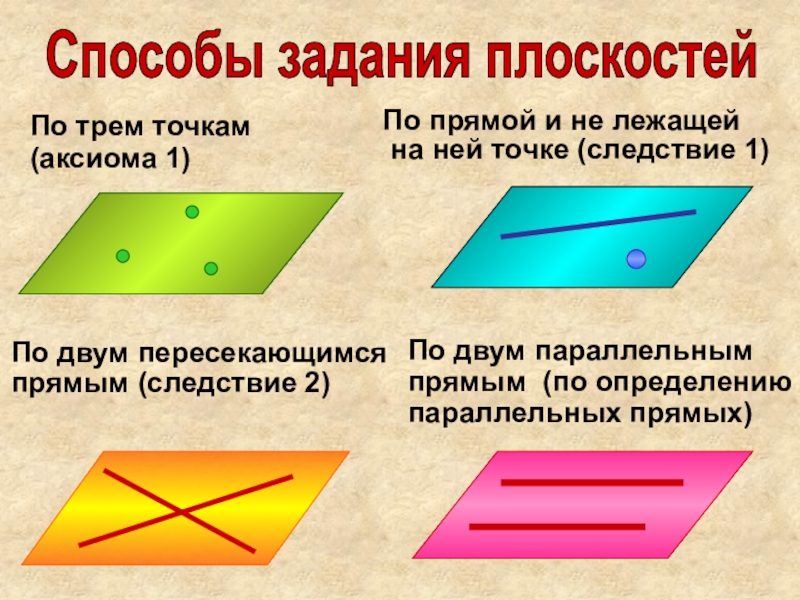
Слайд 11Способы задания плоскостей
По трем точкам
(аксиома 1)
По прямой и не
лежащей
на ней точке (следствие 1)
По двум пересекающимся
прямым (следствие
2)По двум параллельным прямым (по определению параллельных прямых)
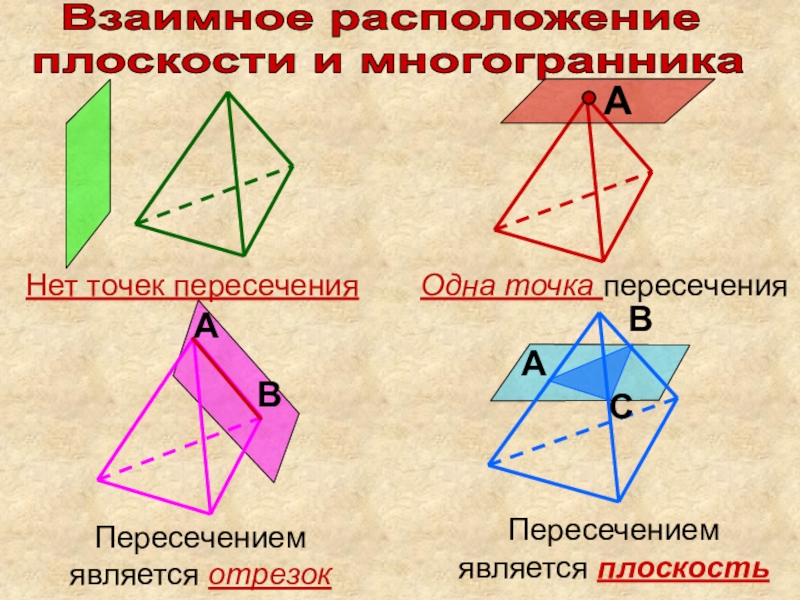
Слайд 12Взаимное расположение
плоскости и многогранника
В
А
Нет точек пересечения
Одна точка пересечения
Пересечением
является
отрезок
Пересечением
является плоскость
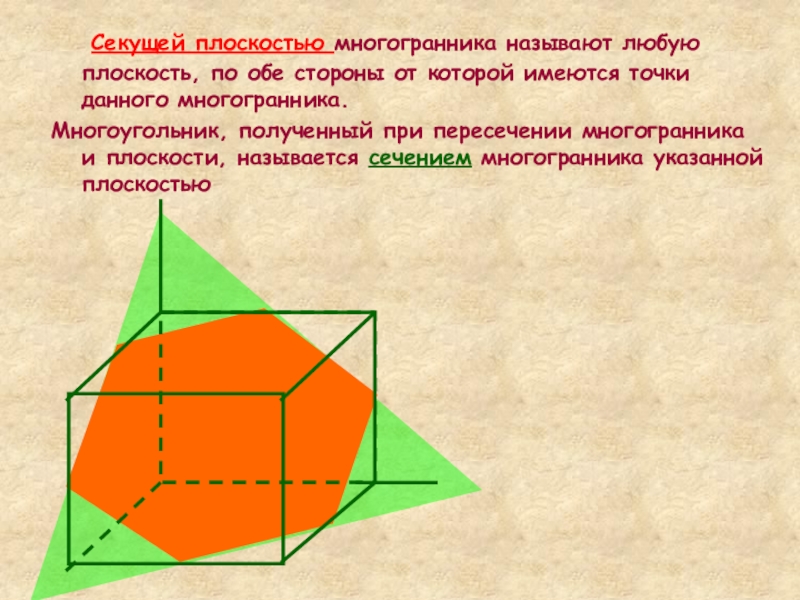
Слайд 13 Секущей плоскостью многогранника называют любую плоскость, по обе стороны от
которой имеются точки данного многогранника.
Многоугольник, полученный при пересечении многогранника
и плоскости, называется сечением многогранника указанной плоскостью
Слайд 14Используя полученные знания, применим их к построению сечений многогранников на
основе аксиоматики.
ПРОБЛЕМА!!!
Слайд 15Алгоритм построения сечения
Построить точки пересечения секущей плоскости с ребрами многогранника.
Полученные
точки, лежащие в одной грани, соединить отрезками.
Многоугольник, ограниченный данными отрезками,
и есть построенное сечение.Замечание: если секущая плоскость пересекает противоположные грани параллелепипеда по каким – либо отрезкам, то эти отрезки параллельны.
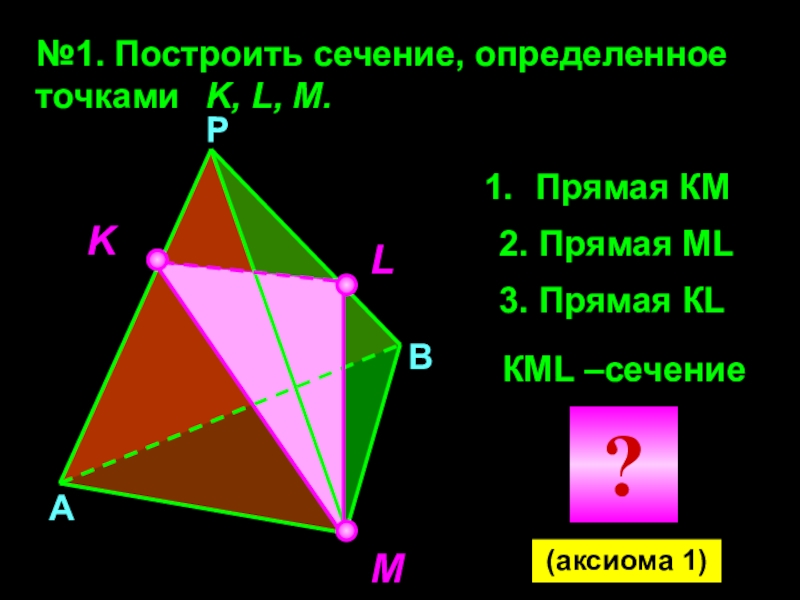
Слайд 16№1. Построить сечение, определенное точками K, L, M.
K
M
L
Прямая
КМ
2. Прямая МL
3. Прямая КL
КМL –сечение
А
В
Р
(аксиома 1)
?
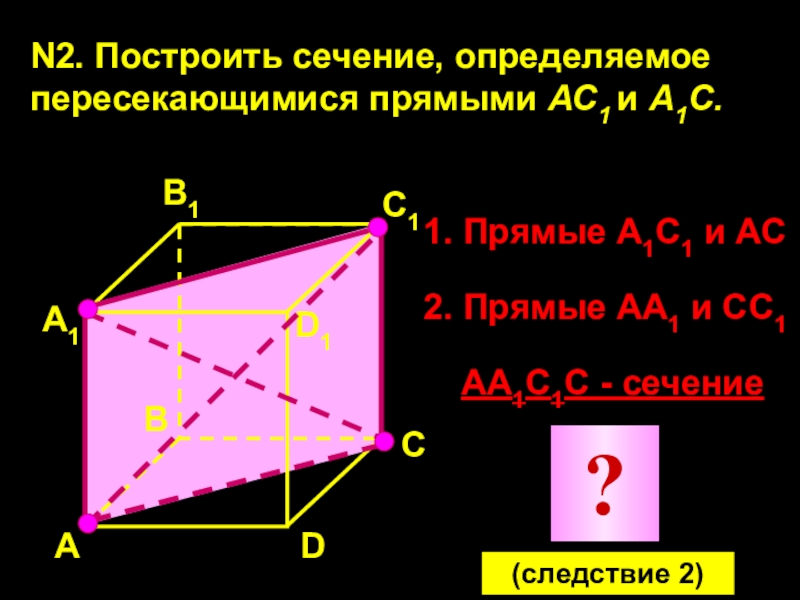
Слайд 17N2. Построить сечение, определяемое пересекающимися прямыми АС1 и А1С.
А
А1
В1
С1
D1
D
В
С
1.
Прямые А1С1 и АС
2. Прямые АА1 и СС1
АА1С1С - сечение
?
(следствие
2)
Слайд 18А
А1
В1
С1
D1
D
С
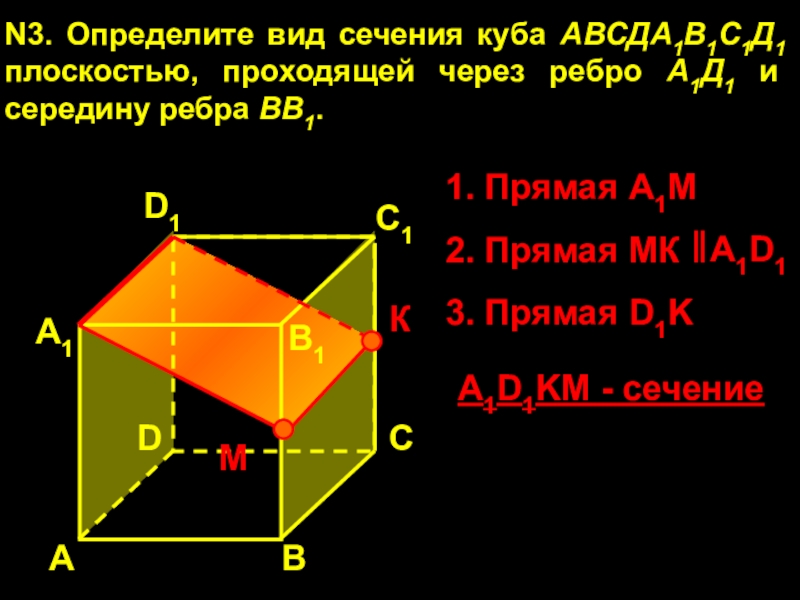
N3. Определите вид сечения куба АВСДА1В1С1Д1 плоскостью, проходящей через ребро
А1Д1 и середину ребра ВВ1.
В
1. Прямая А1М
3. Прямая D1K
A1D1KM -
сечение
Слайд 19А
А1
В1
С1
D1
D
В
С
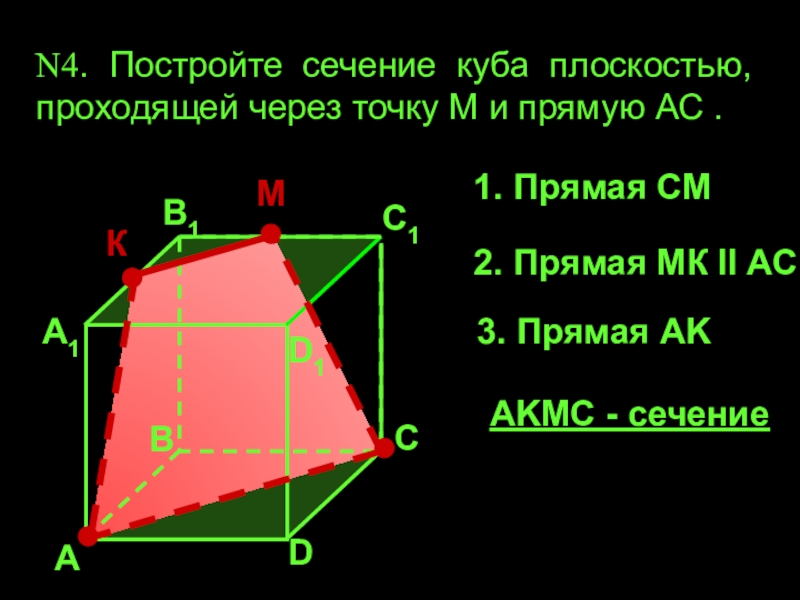
N4. Постройте сечение куба плоскостью, проходящей через точку М и
прямую АС .
М
1. Прямая СМ
2. Прямая МК II AC
3.
Прямая AKAKМС - сечение
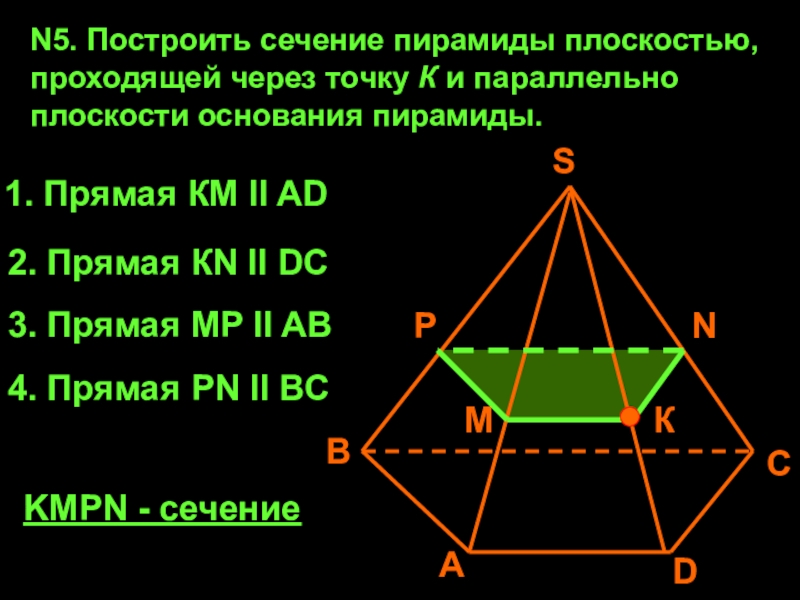
Слайд 20N5. Построить сечение пирамиды плоскостью, проходящей через точку К и
параллельно плоскости основания пирамиды.
А
В
С
D
К
S
1. Прямая КМ II AD
2. Прямая
КN II DCN
M
3. Прямая МP II AB
P
4. Прямая PN II BC
KMPN - сечение
Слайд 21МЕТОД СЛЕДОВ
Суть метода: построение вспомогательной прямой, являющейся линией пересечения секущей
плоскости с плоскостью грани фигуры.
Эту линию называют следом секущей
плоскости. 
Слайд 22М
Р
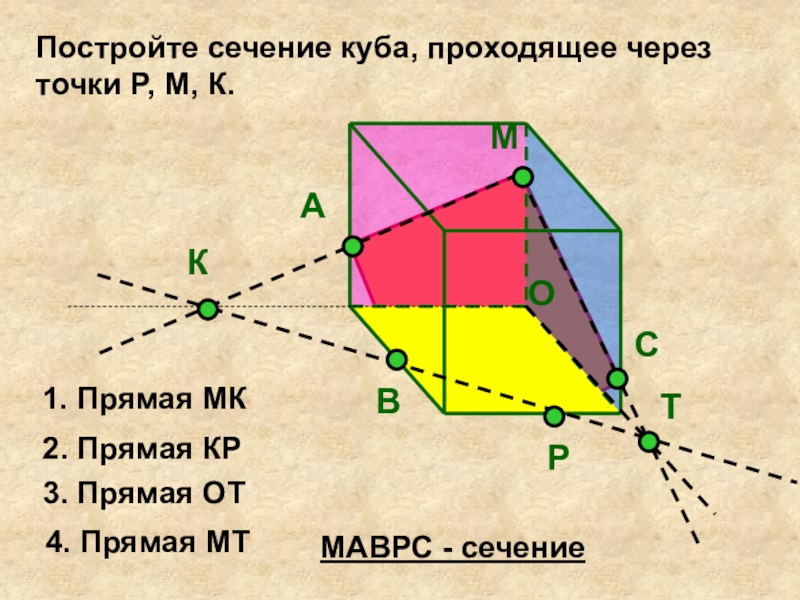
Постройте сечение куба, проходящее через точки P, М, К.
К
А
1.
Прямая МК
В
2. Прямая КР
О
Т
3. Прямая ОТ
МАВРС - сечение
С
4. Прямая МТ
Слайд 27N2. Построить сечение, определяемое параллельными прямыми АА1 и CC1.
А
А1
В1
С1
D1
С
В
D
1.
Прямая А1С1
2. Прямая АС
АА1С1С - сечение
?
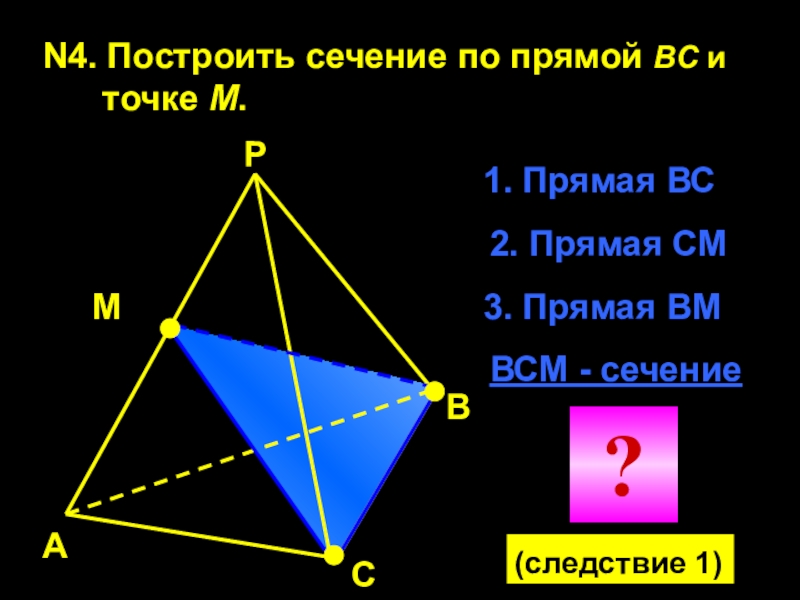
Слайд 28N4. Построить сечение по прямой BC и
точке М.
А
В
С
Р
М
1. Прямая ВС
2. Прямая СМ
ВСМ -
сечение3. Прямая ВМ
?
(следствие 1)
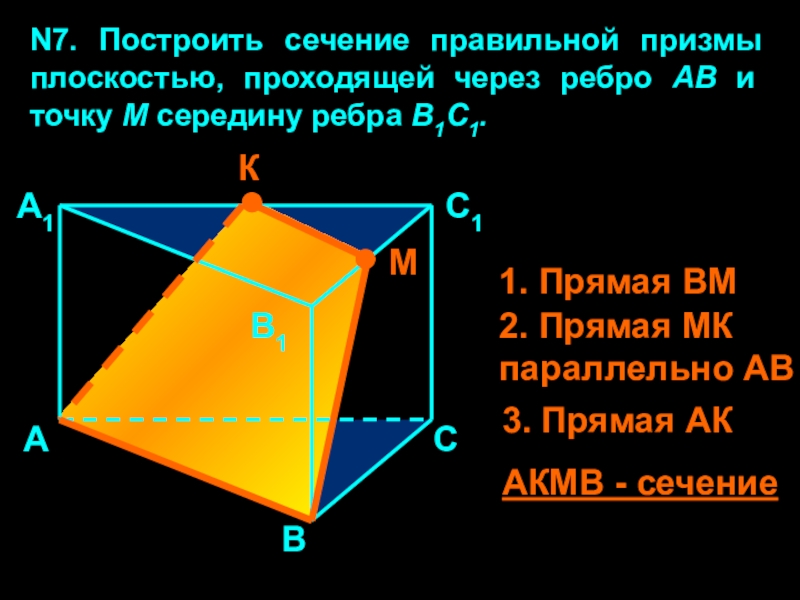
Слайд 29N7. Построить сечение правильной призмы плоскостью, проходящей через ребро АВ
и точку М середину ребра В1С1.
А
В
С
А1
В1
С1
М
1. Прямая ВМ
2. Прямая МК
параллельно АВ3. Прямая АК
АКМВ - сечение
Слайд 30Дана пирамида MABCD. Постройте сечение пирамиды, проходящее через точки P,
Q, R.
1) PR AB=F;
2) FQAD=E;
3)FQBC=T;
4)PTMC=N;
5)PREQNP – ИСКОМОЕ СЕЧЕНИЕ
M
A
B
C
D
R
P
Q
F
