Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПОВЕРХНОСТИ
Содержание
- 1. ПОВЕРХНОСТИ
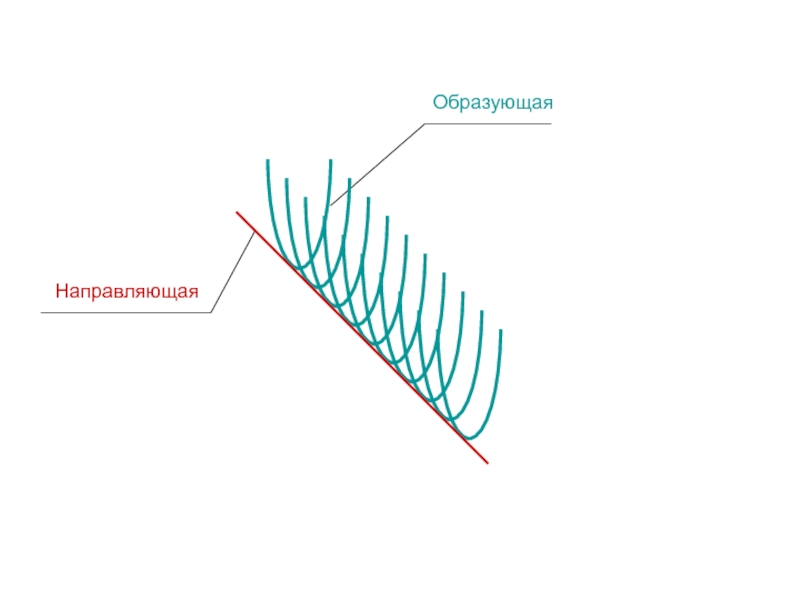
- 2. НаправляющаяОбразующая
- 3. СПОСОБЫ ЗАДАНИЯ ПОВЕРХНОСТЕЙАНАЛИТИЧЕСКИЙ –
- 4. ОЧЕРК ПОВЕРХНОСТИОЧЕРК ПОВЕРХНОСТИ- СЛЕД НА ПЛОСКОСТИ ПРОЕКЦИЙ ОТ ЦИЛИНДРИЧЕСКОЙ ПОВЕРХНОСТИ ОГИБАЮЩЕЙ ЗАДАННУЮ ПОВЕРХНОСТЬ
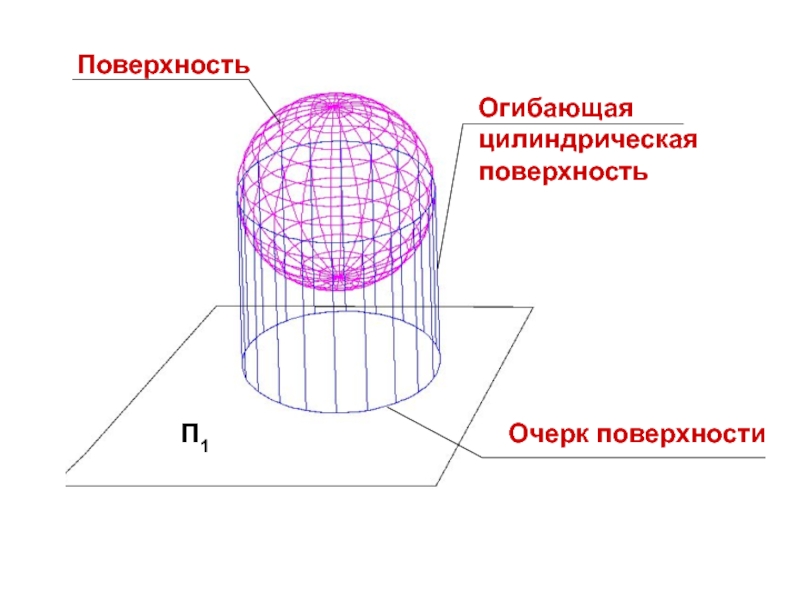
- 5. П1Очерк поверхностиОгибающая цилиндрическая поверхностьПоверхность
- 6. Очерк поверхности
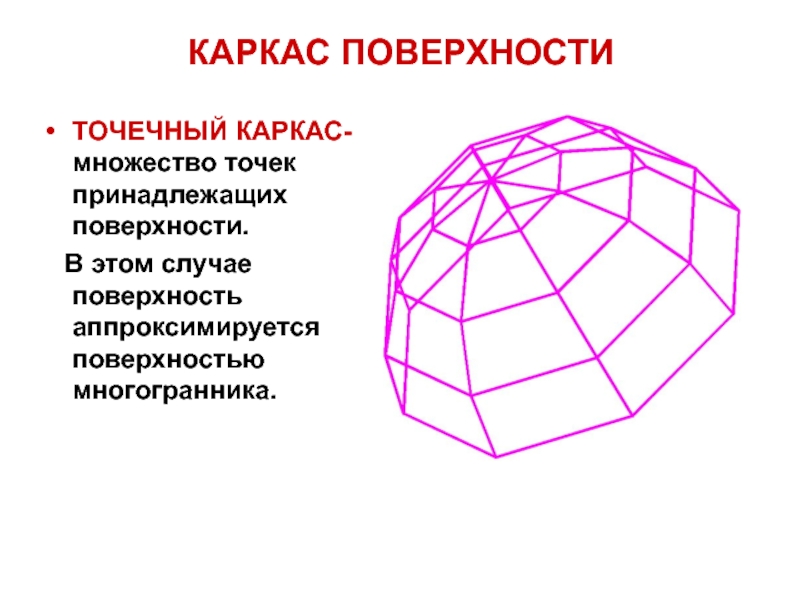
- 7. КАРКАС ПОВЕРХНОСТИТОЧЕЧНЫЙ КАРКАС- множество точек принадлежащих поверхности. В этом случае поверхность аппроксимируется поверхностью многогранника.
- 8. ЛИНЕЙЧАТЫЙ КАРКАС - множество линий, заполняющих поверхность
- 9. ОПРЕДЕЛИТЕЛЬ ПОВЕРХНОСТИ ОПРЕДЕЛИТЕЛЬ- СОВОКУПНОСТЬ ГЕОМЕТРИЧЕСКИХ
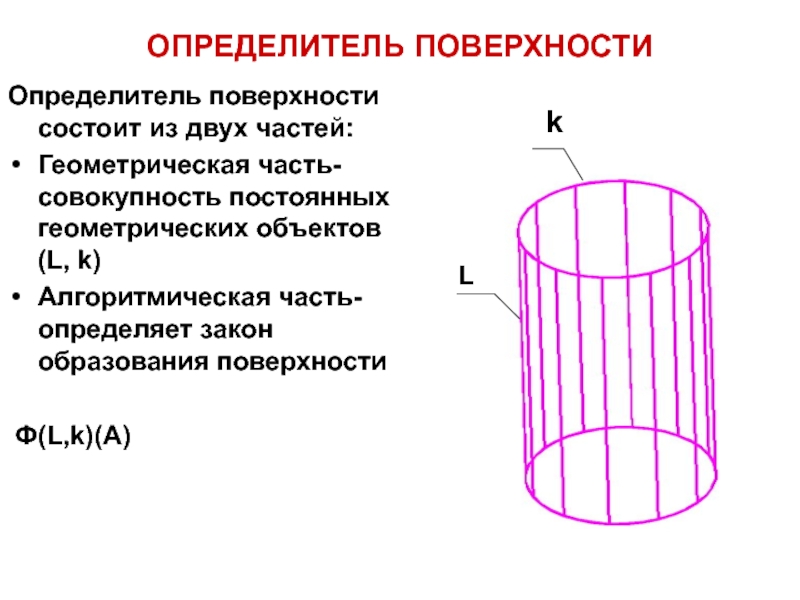
- 10. Определитель поверхности состоит из двух частей:Геометрическая часть-
- 11. КЛАССИФИКАЦИЯ ПОВЕРХНОСТЕЙ
- 12. ПоверхностиЛинейчатая поверхность- образующая прямая линия.Нелинейчатая поверхность- образующая
- 13. Гранные поверхности Многогранники- это замкнутые пространственные фигуры,
- 14. Гранные поверхностиПризма - образуется при движении прямолинейной
- 15. Гранные поверхностиПирамида – образуется при движении прямолинейной
- 16. ПРОСТЕЙШИЕ ПОВЕРХНОСТИ ВРАЩЕНИЯm – образующая поверхностиi –
- 17. ЦИЛИНДРИЧЕСКАЯ ПОВЕРХНОСТЬ ВРАЩЕНИЯi – ось вращения2.
- 18. ПОВЕРХНОСТЬ КОНУСА ВРАЩЕНИЯ1. i – ось вращения2.
- 19. ПОВЕРХНОСТЬ CФЕРЫi – ось вращенияm – криволинейная
- 20. ТОРОВАЯ ПОВЕРХНОСТЬ ОТКРЫТЫЙ ТОРi – ось
- 21. ТОРОВАЯ ПОВЕРХНОСТЬ ЗАКРЫТЫЙ ТОРi – ось
- 22. ТОРОВАЯ ПОВЕРХНОСТЬ САМОПЕРЕСЕКАЮЩИЙСЯ ТОР (тор -
- 23. СЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ Сечение поверхности плоскостью
- 24. СЕЧЕНИЕ ГРАННОЙ ПОВЕРХНОСТИ ПЛОСКОСТЬЮСечение гранной поверхности –
- 25. СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ ПЛОСКОСТЬЮa i – окружностьb ^ i – эллипсg ll i - прямоугольникL2i2i1L1aП2bП2gП111211222
- 26. сечение цилиндра -эллипсСЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ ПЛОСКОСТЬЮbП211212111111 2112122121222113231131313123114142411412414115151152152bП2
- 27. a i – окружностьb ^
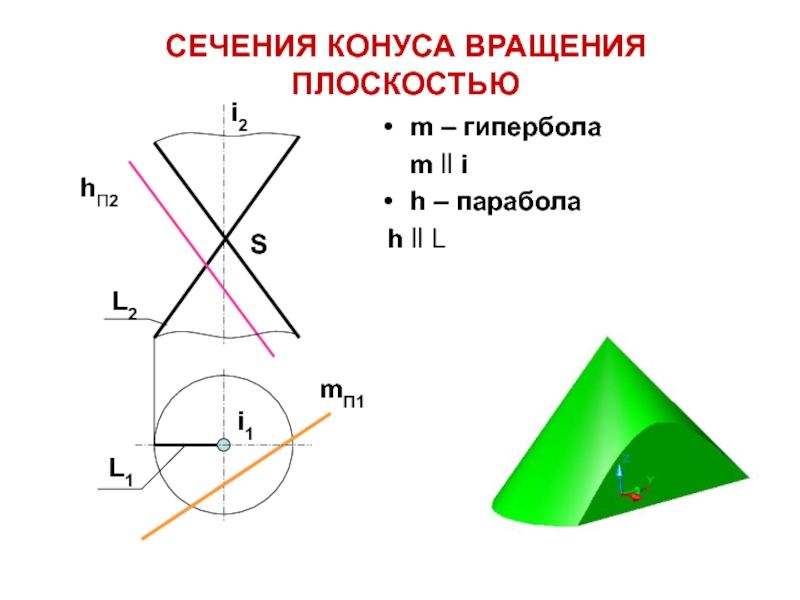
- 28. m – гипербола m ll ih
- 29. 121321421221311311αП112221121μП2R4232βП2R31314141111221411411СЕЧЕНИЕ КОНУСА ВРАЩЕНИЯ ПЛОСКОСТЬЮ (эллипс)
- 30. СЕЧЕНИЯ СФЕРЫ ПЛОСКОСТЬЮ Сечение сферы плоскостью
- 31. СЕЧЕНИЯ СФЕРЫ ПЛОСКОСТЬЮαп212112221323131142bп241141gп25251511Точка принадлежит поверхности, если она принадлежит линии, принадлежащей в свою очередь этой поверхности
- 32. Через прямую m проводим вспомогательную плоскость-посредник П2Строим
- 33. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1ПОВЕРХНОСТИ
ПОВЕРХНОСТЬ
МНОЖЕСТВО ПОЛОЖЕНИЙ ЛИНИИ ПЕРЕМЕЩАЮЩЕЙСЯ В ПРОСТРАНСТВЕ ПО ОПРЕДЕЛЕННОМУ ЗАКОНУ
ЛИНИЯ ПЕРЕМЕЩАЮЩАЯСЯ
В ПРОСТРАНСТВЕ НАЗЫВАЕТСЯ ОБРАЗУЮЩАЯ
Слайд 3СПОСОБЫ ЗАДАНИЯ ПОВЕРХНОСТЕЙ
АНАЛИТИЧЕСКИЙ –
X2 +
Y2 + Z2 =1
2. ГРАФИЧЕСКИЙ:
а. очеркб. каркас
в. определитель
Слайд 4ОЧЕРК ПОВЕРХНОСТИ
ОЧЕРК ПОВЕРХНОСТИ-
СЛЕД НА ПЛОСКОСТИ ПРОЕКЦИЙ ОТ ЦИЛИНДРИЧЕСКОЙ ПОВЕРХНОСТИ
ОГИБАЮЩЕЙ ЗАДАННУЮ
ПОВЕРХНОСТЬ
Слайд 7КАРКАС ПОВЕРХНОСТИ
ТОЧЕЧНЫЙ КАРКАС- множество точек принадлежащих поверхности.
В этом
случае поверхность аппроксимируется поверхностью многогранника.
Слайд 8ЛИНЕЙЧАТЫЙ КАРКАС -
множество линий, заполняющих поверхность так, что через
каждую точку поверхности проходит одна линия каркаса
Слайд 9ОПРЕДЕЛИТЕЛЬ ПОВЕРХНОСТИ
ОПРЕДЕЛИТЕЛЬ- СОВОКУПНОСТЬ
ГЕОМЕТРИЧЕСКИХ ЭЛЕМЕНТОВ ОПРЕДЕЛЯЮЩИХ ПОВЕРХНОСТЬ
И ЗАКОНОМЕРНОСТЬ, ОПИСЫВАЮЩАЯ ИХ ДВИЖЕНИЕ В ПРОСТРАНСТВЕ
Слайд 10Определитель поверхности состоит из двух частей:
Геометрическая часть- совокупность постоянных геометрических
объектов (L, k)
Алгоритмическая часть- определяет закон образования поверхности
Ф(L,k)(A)
ОПРЕДЕЛИТЕЛЬ ПОВЕРХНОСТИ
L
k
Слайд 12Поверхности
Линейчатая поверхность- образующая прямая линия.
Нелинейчатая поверхность- образующая кривая линия постоянной
или переменной формы.
Развертываемые поверхности- поверхности, которые можно без складок и
разрывов развернуть на плоскость.Неразвертываемые поверхности- поверхности, которые нельзя без складок и разрывов развернуть на плоскость.
Слайд 13Гранные поверхности
Многогранники- это замкнутые пространственные фигуры, ограниченные плоскими многоугольниками.
Эти
многоугольники называются гранями
их стороны –ребрами
вершины –вершинами многогранника.
Слайд 14Гранные поверхности
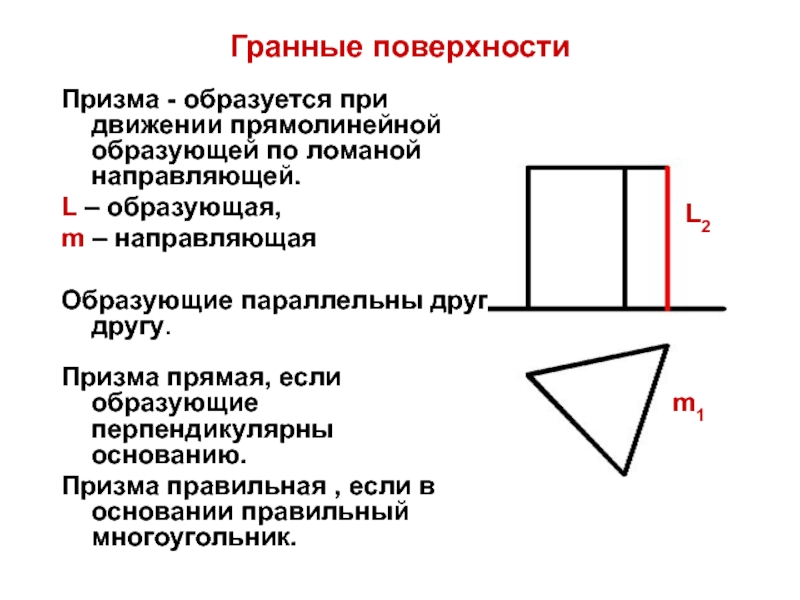
Призма - образуется при движении прямолинейной образующей по ломаной
направляющей.
L – образующая,
m – направляющая
Образующие параллельны друг другу.
Призма прямая,
если образующие перпендикулярны основанию.Призма правильная , если в основании правильный многоугольник.
Слайд 15Гранные поверхности
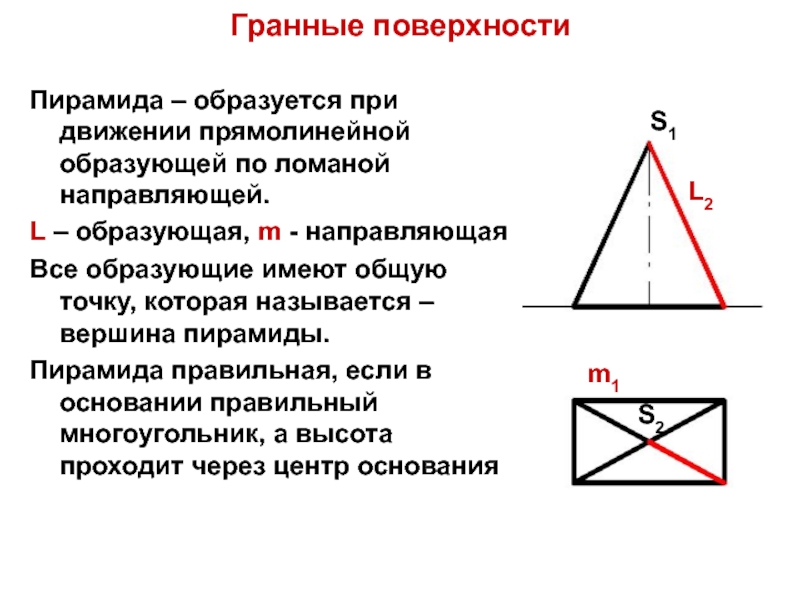
Пирамида – образуется при движении прямолинейной образующей по ломаной
направляющей.
L – образующая, m - направляющая
Все образующие имеют общую точку,
которая называется – вершина пирамиды.Пирамида правильная, если в основании правильный многоугольник, а высота проходит через центр основания
S1
S2
Слайд 16ПРОСТЕЙШИЕ ПОВЕРХНОСТИ ВРАЩЕНИЯ
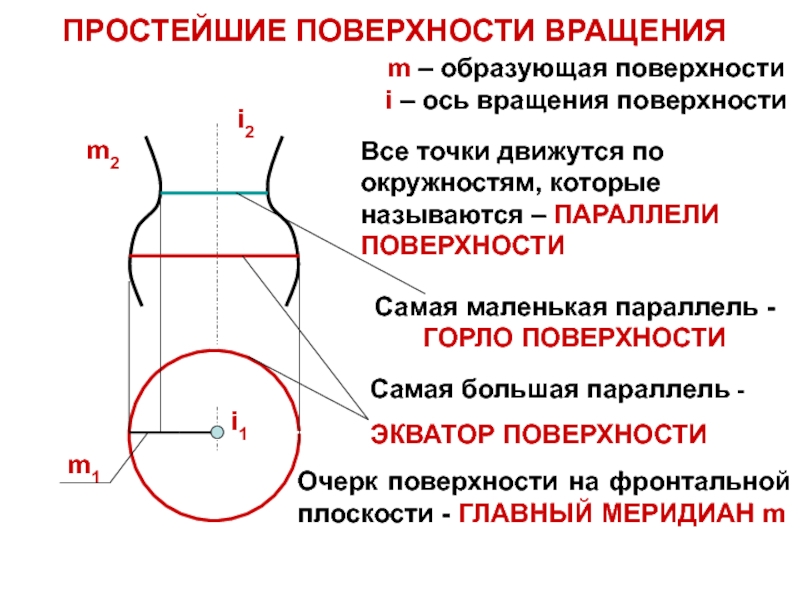
m – образующая поверхности
i – ось вращения поверхности
Самая
маленькая параллель - ГОРЛО ПОВЕРХНОСТИ
Самая большая параллель -
ЭКВАТОР ПОВЕРХНОСТИ
Очерк
поверхности на фронтальной плоскости - ГЛАВНЫЙ МЕРИДИАН mВсе точки движутся по окружностям, которые называются – ПАРАЛЛЕЛИ ПОВЕРХНОСТИ
m2
m1
i2
i1
Слайд 17ЦИЛИНДРИЧЕСКАЯ ПОВЕРХНОСТЬ ВРАЩЕНИЯ
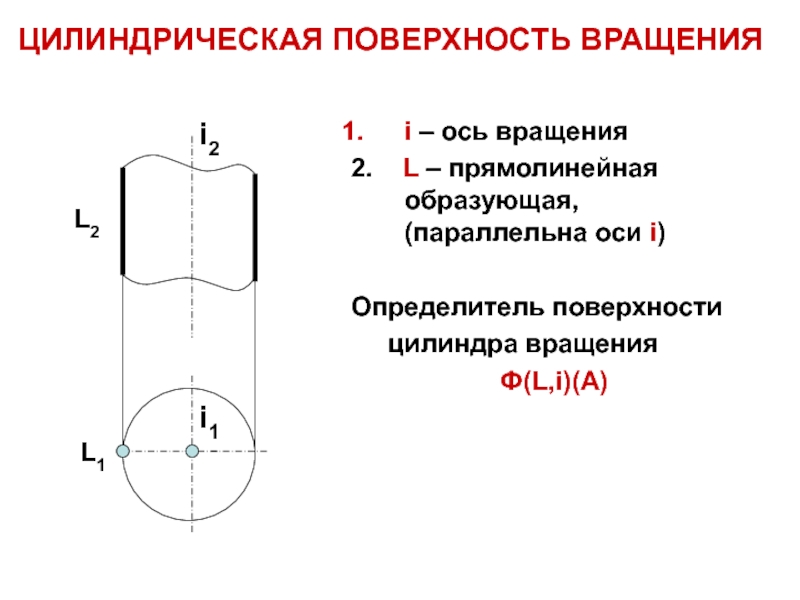
i – ось вращения
2. L – прямолинейная
образующая, (параллельна оси i)
Определитель поверхности
цилиндра вращения
Ф(L,i)(A)
L2
i2
i1
L1
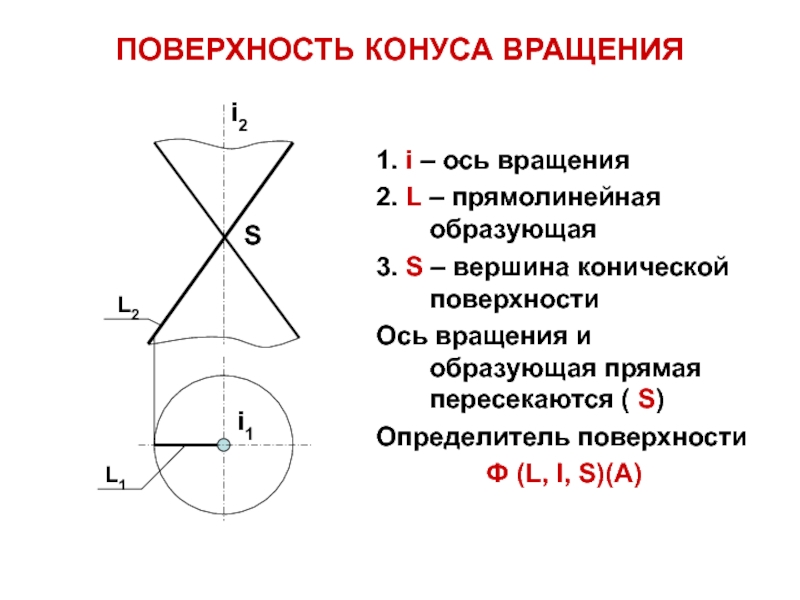
Слайд 18ПОВЕРХНОСТЬ КОНУСА ВРАЩЕНИЯ
1. i – ось вращения
2. L – прямолинейная
образующая
3. S – вершина конической поверхности
Ось вращения и образующая прямая
пересекаются ( S)Определитель поверхности
Ф (L, I, S)(A)
L2
L1
i2
i1
S
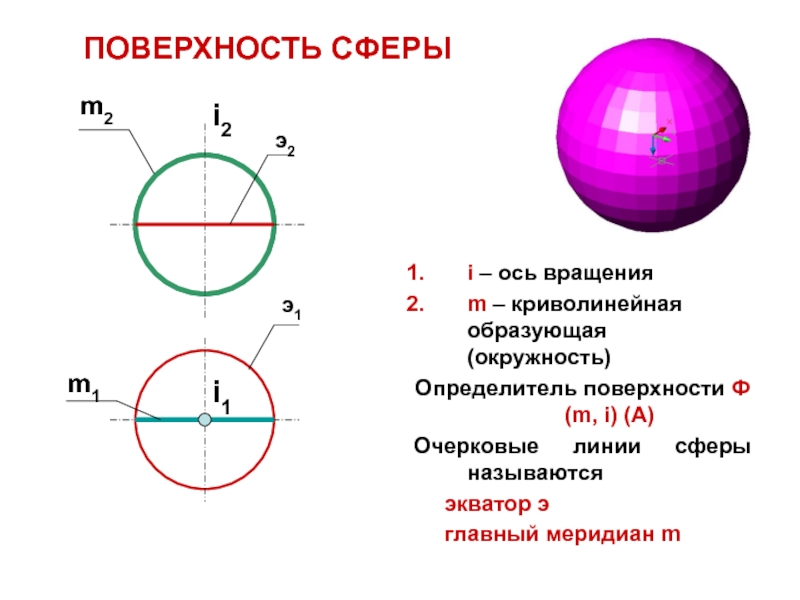
Слайд 19ПОВЕРХНОСТЬ CФЕРЫ
i – ось вращения
m – криволинейная образующая (окружность)
Определитель поверхности
Ф(m, i) (A)
Очерковые линии сферы называются
экватор э
главный меридиан mm2
m1
i2
i1
э2
э1
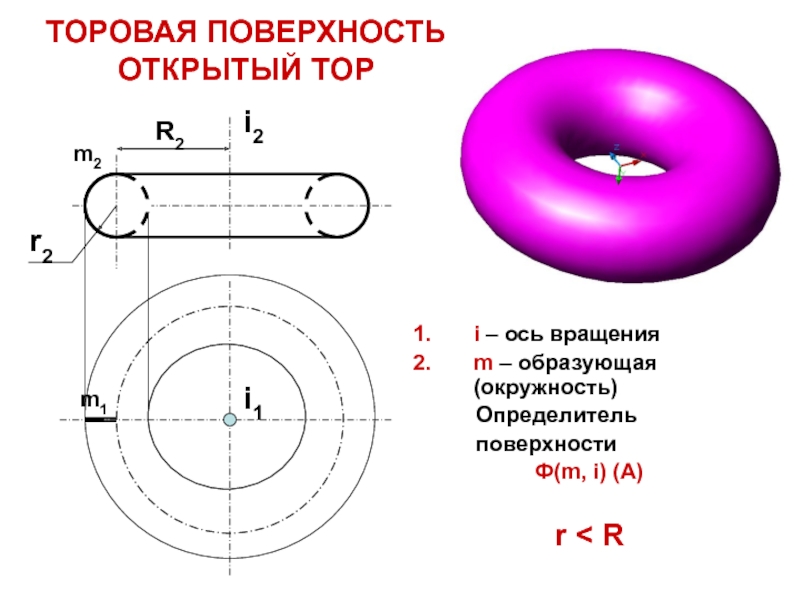
Слайд 20ТОРОВАЯ ПОВЕРХНОСТЬ
ОТКРЫТЫЙ ТОР
i – ось вращения
m – образующая (окружность)
Определитель
поверхностиФ(m, i) (A)
r < R
i2
m2
m1
i1
r2
R2
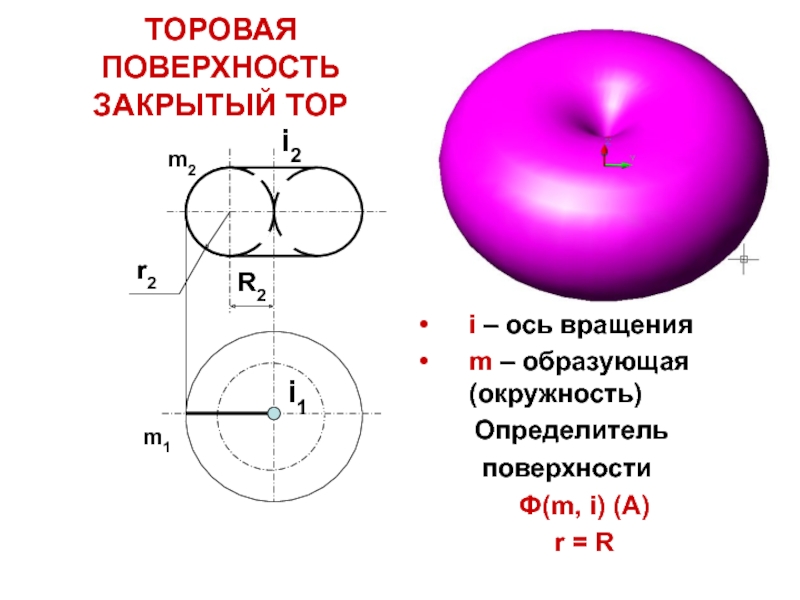
Слайд 21ТОРОВАЯ ПОВЕРХНОСТЬ
ЗАКРЫТЫЙ ТОР
i – ось вращения
m – образующая (окружность)
Определитель
поверхностиФ(m, i) (A)
r = R
i2
m2
m1
i1
r2
R2
Слайд 22ТОРОВАЯ ПОВЕРХНОСТЬ
САМОПЕРЕСЕКАЮЩИЙСЯ ТОР (тор - бочка)
1. i – ось
вращения
2. m – образующая (окружность)
Определитель
поверхности
Ф(m, i) (A)
r > R
R2
r2
i2
m2
m1
i1
R2
Слайд 23СЕЧЕНИЕ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ
Сечение поверхности плоскостью –
линия пересечения поверхности и плоскости.
Точка принадлежит поверхности, если она
принадлежит линии, принадлежащей в свою очередь этой поверхностиСлайд 24СЕЧЕНИЕ ГРАННОЙ ПОВЕРХНОСТИ ПЛОСКОСТЬЮ
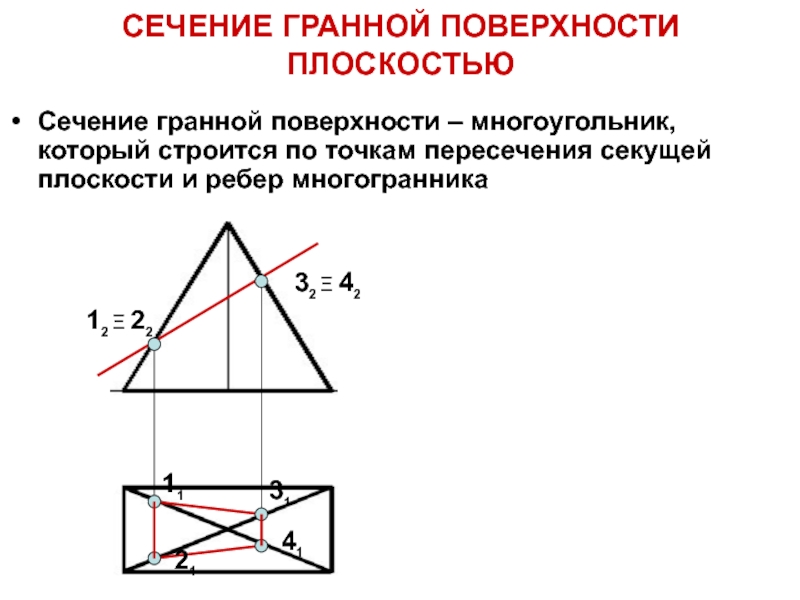
Сечение гранной поверхности – многоугольник, который строится
по точкам пересечения секущей плоскости и ребер многогранника
12 Ξ 22
32
Ξ 4211
21
41
31
Слайд 25СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ ПЛОСКОСТЬЮ
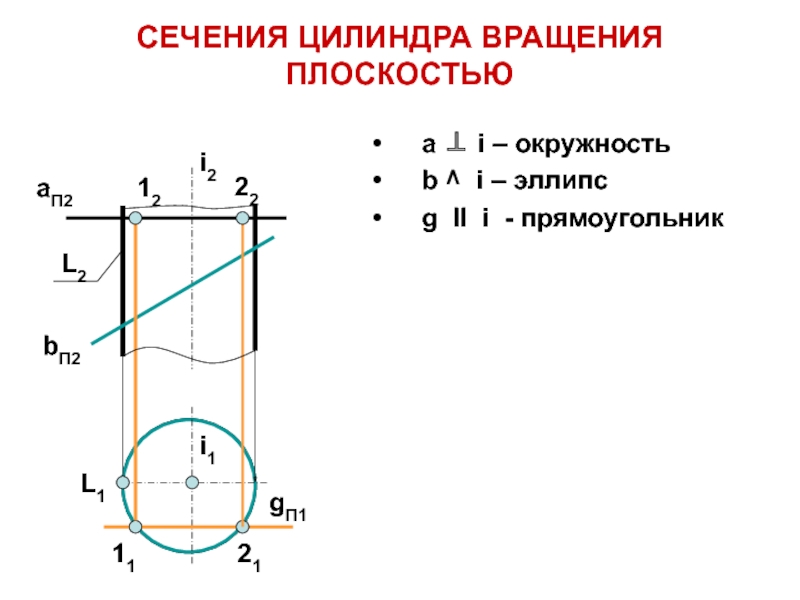
a i – окружность
b ^ i
– эллипс
g ll i - прямоугольник
L2
i2
i1
L1
aП2
bП2
gП1
11
21
12
22
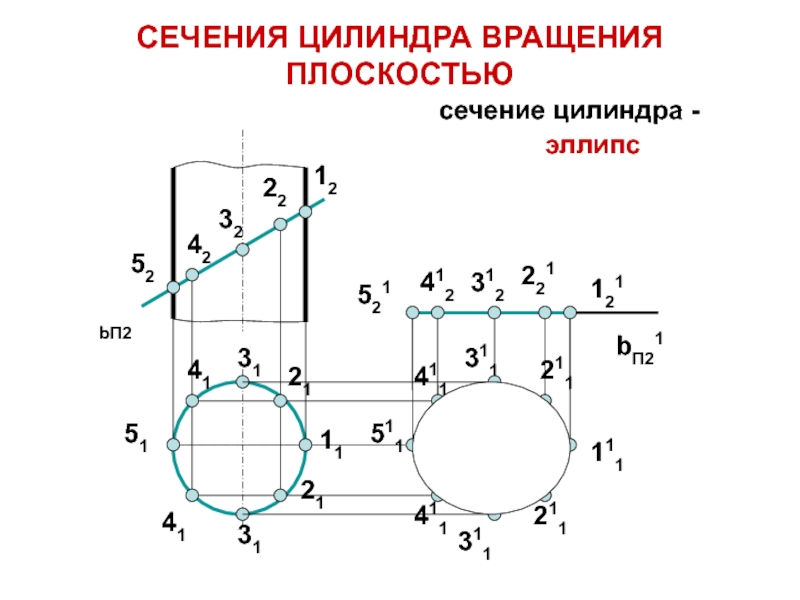
Слайд 26сечение цилиндра -
эллипс
СЕЧЕНИЯ ЦИЛИНДРА ВРАЩЕНИЯ ПЛОСКОСТЬЮ
bП21
12
121
11
111
211
21
221
21
22
211
32
311
31
31
312
311
41
42
411
412
41
411
51
511
521
52
bП2
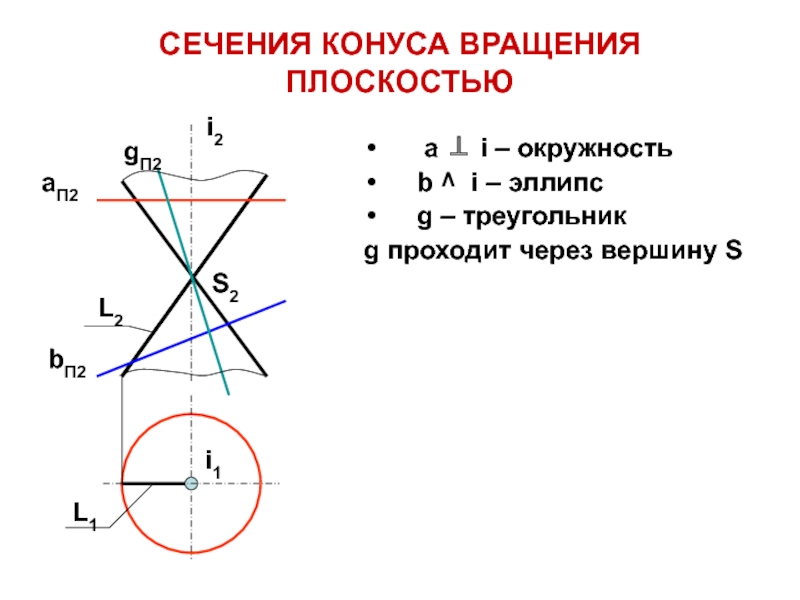
Слайд 27 a i – окружность
b ^ i – эллипс
g
– треугольник
g проходит через вершину S
СЕЧЕНИЯ КОНУСА ВРАЩЕНИЯ ПЛОСКОСТЬЮ
L2
L1
i2
i1
S2
aП2
bП2
gП2
Слайд 29121
321
421
221
311
311
αП1
12
22
11
21
μП2
R
42
32
βП2
R
31
31
41
41
111
221
411
411
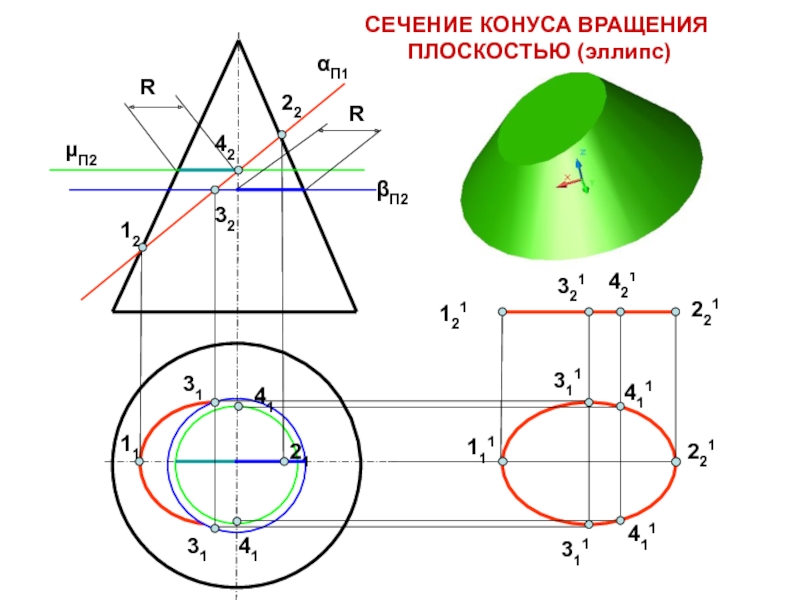
СЕЧЕНИЕ КОНУСА ВРАЩЕНИЯ
ПЛОСКОСТЬЮ (эллипс)
Слайд 30СЕЧЕНИЯ СФЕРЫ ПЛОСКОСТЬЮ
Сечение сферы плоскостью – окружность, которая
может проецироваться как:
прямая линия
окружностьэллипс
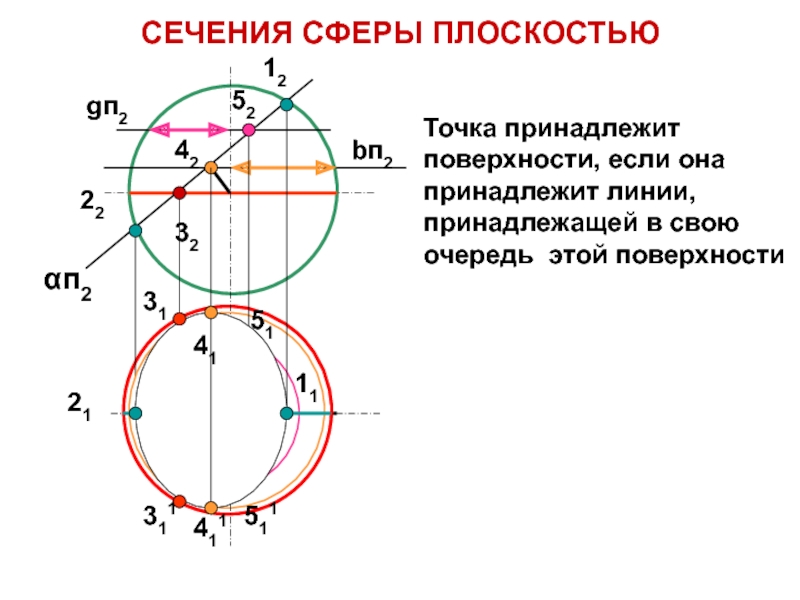
Слайд 31СЕЧЕНИЯ СФЕРЫ ПЛОСКОСТЬЮ
αп2
12
11
22
21
32
31
311
42
bп2
411
41
gп2
52
51
511
Точка принадлежит поверхности, если она принадлежит линии, принадлежащей
в свою очередь этой поверхности
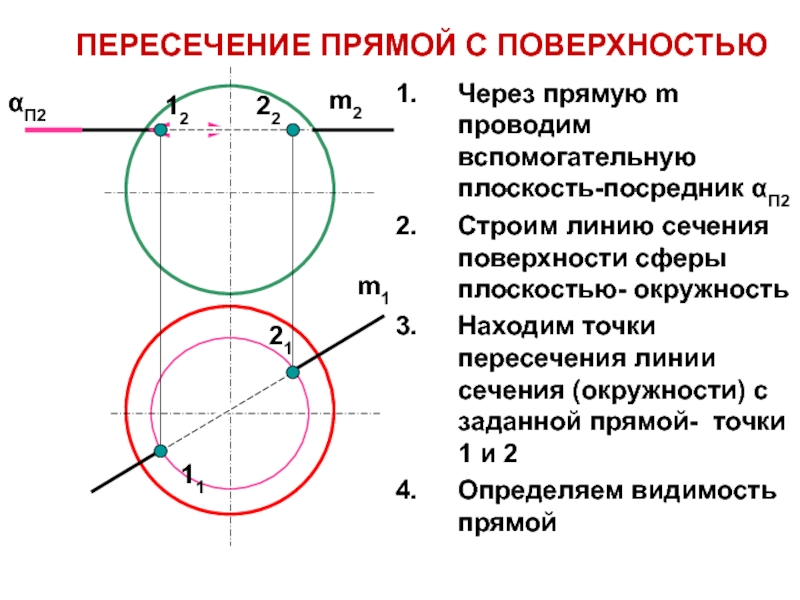
Слайд 32Через прямую m проводим вспомогательную плоскость-посредник П2
Строим линию сечения поверхности
сферы плоскостью- окружность
Находим точки пересечения линии сечения (окружности) с заданной
прямой- точки 1 и 2Определяем видимость прямой
ПЕРЕСЕЧЕНИЕ ПРЯМОЙ С ПОВЕРХНОСТЬЮ
m2
П2
m1
21
11
22
12