Слайд 2Двоичное кодирование в компьютере
Вся информация, которую обрабатывает компьютер должна быть
представлена двоичным кодом с помощью двух цифр: 0 и 1.
Эти два символа принято называть двоичными цифрами или битами.
С помощью двух цифр 0 и 1 можно закодировать любое сообщение. Это явилось причиной того, что в компьютере обязательно должно быть организованно два важных процесса: кодирование и декодирование.
Кодирование – преобразование входной информации в форму, воспринимаемую компьютером, т.е. двоичный код.
Декодирование – преобразование данных из двоичного кода в форму, понятную человеку.
Слайд 3Почему двоичное кодирование
С точки зрения технической реализации использование двоичной системы
счисления для кодирования информации оказалось намного более простым, чем применение
других способов. Действительно, удобно кодировать информацию в виде последовательности нулей и единиц, если представить эти значения как два возможных устойчивых состояния электронного элемента:
0 – отсутствие электрического сигнала;
1 – наличие электрического сигнала.
Эти состояния легко различать. Недостаток двоичного кодирования – длинные коды. Но в технике легче иметь дело с большим количеством простых элементов, чем с небольшим числом сложных.
Способы кодирования и декодирования информации в компьютере, в первую очередь, зависит от вида информации, а именно, что должно кодироваться: числа, текст, графические изображения или звук.
Слайд 4Система счисления
Для записи информации о количестве объектов используются числа.
Числа записываются с помощью набора специальных символов.
Система счисления — способ
записи чисел с помощью набора специальных знаков, называемых цифрами.
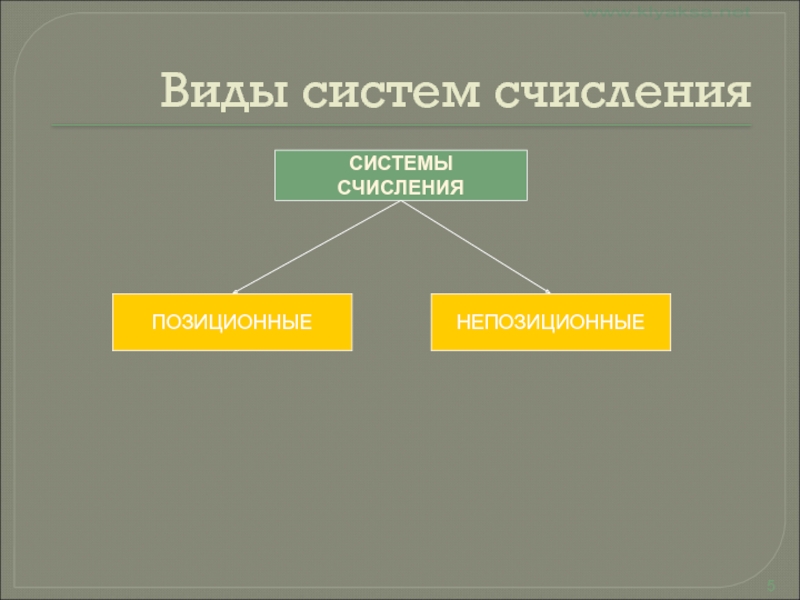
Слайд 5Виды систем счисления
СИСТЕМЫ СЧИСЛЕНИЯ
ПОЗИЦИОННЫЕ
НЕПОЗИЦИОННЫЕ
Слайд 6Непозиционные системы счисления
Каноническим примером фактически непозиционной системы счисления является римская,
в которой в качестве цифр используются латинские буквы:
I обозначает
1, V - 5, X - 10, L - 50, C - 100, D - 500, M -1000.
Натуральные числа записываются при помощи повторения этих цифр.
Например, II = 1 + 1 = 2, здесь символ I обозначает 1 независимо от места в числе.
Для правильной записи больших чисел римскими цифрами необходимо сначала записать число тысяч, затем сотен, затем десятков и, наконец, единиц.
Слайд 7Позиционные системы счисления
В позиционных системах счисления величина, обозначаемая цифрой в
записи числа, зависит от её положения в числе (позиции).
Количество
используемых цифр называется основанием системы счисления.
Например, 11 – это одиннадцать, а не два: 1 + 1 = 2 (сравните с римской системой счисления). Здесь символ 1 имеет различное значение в зависимости от позиции в числе.
Слайд 8Первые позиционные системы счисления
Самой первой такой системой, когда счетным "прибором"
служили пальцы рук, была пятеричная.
Некоторые племена на филиппинских островах
используют ее и в наши дни, а в цивилизованных странах ее реликт, как считают специалисты, сохранился только в виде школьной пятибалльной шкалы оценок.
Слайд 9Двенадцатеричная система счисления
Следующей после пятеричной возникла двенадцатеричная система счисления. Возникла
она в древнем Шумере. Некоторые учёные полагают, что такая система
возникала у них из подсчёта фаланг на руке большим пальцем.
Широкое распространение получила двенадцатеричная система счисления в XIX веке. На ее широкое использование в прошлом явно указывают названия числительных во многих языках, а также сохранившиеся в ряде стран способы отсчета времени, денег и соотношения между некоторыми единицами измерения. Год состоит из 12 месяцев, а половина суток состоит из 12 часов.
Элементом двенадцатеричной системы в современности может служить счёт дюжинами. Первые три степени числа 12 имеют собственные названия: 1 дюжина = 12 штук; 1 гросс = 12 дюжин = 144 штуки; 1 масса = 12 гроссов = 144 дюжины = 1728 штук.
Английский фунт состоит из 12 шиллингов.
Слайд 10Шестидесятеричная система счисления
Следующая позиционная система счисления была придумана еще в
Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричная, т.е. в ней
использовалось шестьдесят цифр!
В более позднее время использовалась арабами, а также древними и средневековыми астрономами. Шестидесятеричная система счисления, как считают исследователи, являет собой синтез уже вышеупомянутых пятеричной и двенадцатеричной систем.
Слайд 11Какие позиционные системы счисления используются сейчас?
В настоящее время наиболее распространены
десятичная, двоичная, восьмеричная и шестнадцатеричная системы счисления.
Двоичная, восьмеричная (в
настоящее время вытесняется шестнадцатеричной) и шестнадцатеричная система часто используется в областях, связанных с цифровыми устройствами, программировании и вообще компьютерной документации.
Современные компьютерные системы оперируют информацией представленной в цифровой форме. Числовые данные преобразуются в двоичную систему счисления.
Слайд 12Десятичная система счисления
Десятичная система счисления — позиционная система счисления
по основанию 10.
Предполагается, что основание 10 связано с количеством пальцев
рук у человека.
Наиболее распространённая система счисления в мире.
Для записи чисел используются символы 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, называемые арабскими цифрами.
Слайд 13Двоичная система счисления
Двоичная система счисления — позиционная система счисления
с основанием 2. Используются цифры 0 и 1.
Двоичная система используется
в цифровых устройствах, поскольку является наиболее простой и удовлетворяет требованиям:
Чем меньше значений существует в системе, тем проще изготовить отдельные элементы.
Чем меньше количество состояний у элемента, тем выше помехоустойчивость и тем быстрее он может работать.
Простота создания таблиц сложения и умножения — основных действий над числами
Слайд 14Алфавит десятичной, двоичной, восьмеричной и шестнадцатеричной систем счисления
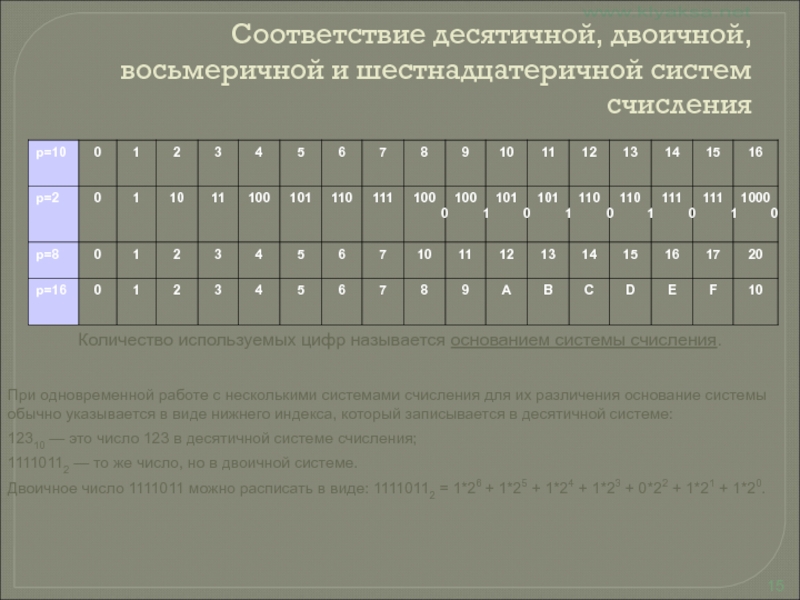
Слайд 15Соответствие десятичной, двоичной, восьмеричной и шестнадцатеричной систем счисления
Количество используемых цифр
называется основанием системы счисления.
При одновременной работе с несколькими системами счисления
для их различения основание системы обычно указывается в виде нижнего индекса, который записывается в десятичной системе:
12310 — это число 123 в десятичной системе счисления;
11110112 — то же число, но в двоичной системе.
Двоичное число 1111011 можно расписать в виде: 11110112 = 1*26 + 1*25 + 1*24 + 1*23 + 0*22 + 1*21 + 1*20.
Слайд 16Перевод чисел из одной системы счисления в другую
Чтобы перевести число
из позиционной системы счисления с основанием p в десятичную, надо
представить это число в виде суммы степеней p и произвести указанные вычисления в десятичной системе счисления.
Например, переведем число 10112 в десятичную систему счисления. Для этого представим это число в виде степеней двойки и произведем вычисления в десятичной системе счисления.
10112 = 1*23 + 0*22 + 1*21 + 1*20 = 1*8 + 0*4 + 1*2 + 1*1 = 8 + 0 + 2 + 1 = 1110
Рассмотрим еще один пример. Переведем число 52,748 в десятичную систему счисления.
52,748 = 5*81 + 2*80 + 3*8-1 + 4*8-2 = 5*8 + 2*1 + 7*1/8 +4*1/49 = 40 + 2 + 0,875 + 0,0625 = 42,937510
Слайд 17Перевод чисел из одной системы счисления в другую
Перевод из десятичной
системы счисления в систему счисления с основанием p осуществляется последовательным
делением десятичного числа и его десятичных частных на p, а затем выписыванием последнего частного и остатков в обратном порядке.
Переведем десятичное число 2010 в двоичную систем счисления (основание системы счисления p=2). В итоге получили 2010 = 101002.
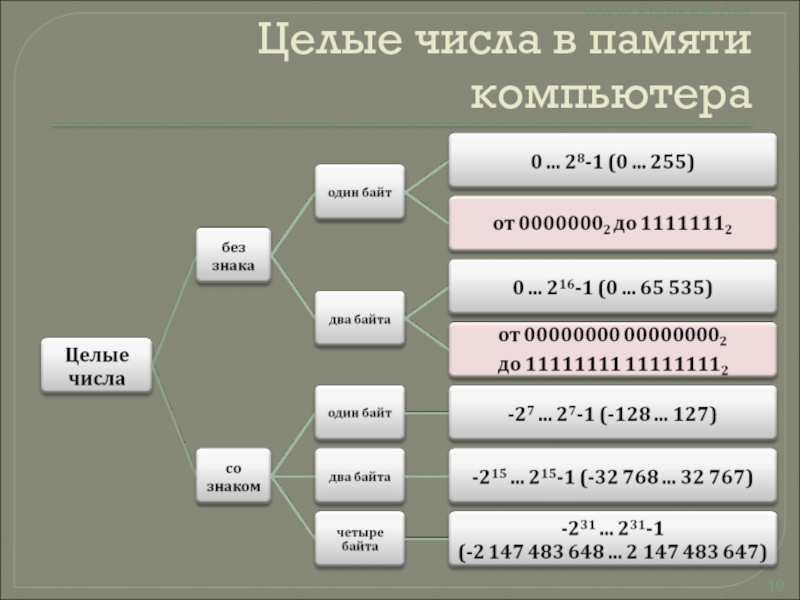
Слайд 18Числа в компьютере
Числа в компьютере хранятся и обрабатываются в двоичной
системе счисления. Последовательность нулей и единиц называют двоичным кодом.
Слайд 20Числа без знака
Число 3910 = 100111 2 в однобайтовом формате:
Число
3910 = 100111 2 в двубайтовом формате:
Число 65 53510 =
11111111 111111112 в двубайтовом формате:
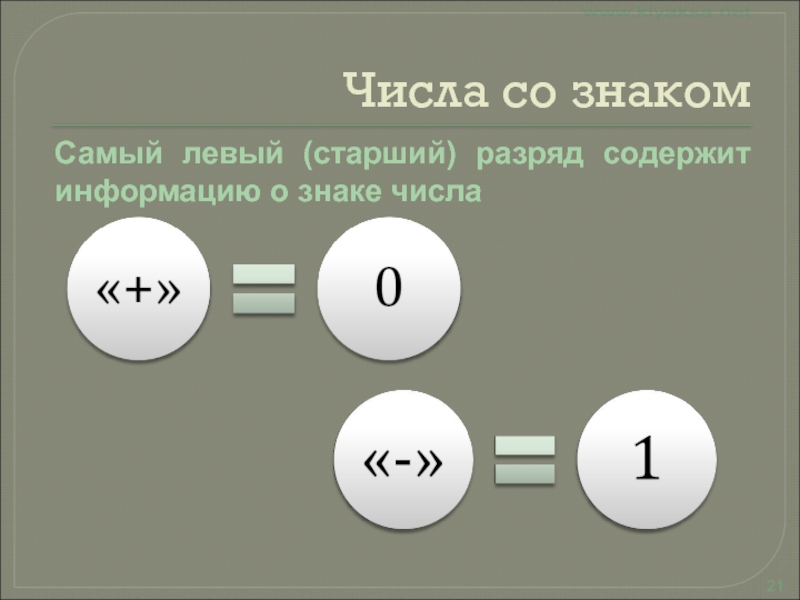
Слайд 21Числа со знаком
Самый левый (старший) разряд содержит информацию о знаке
числа
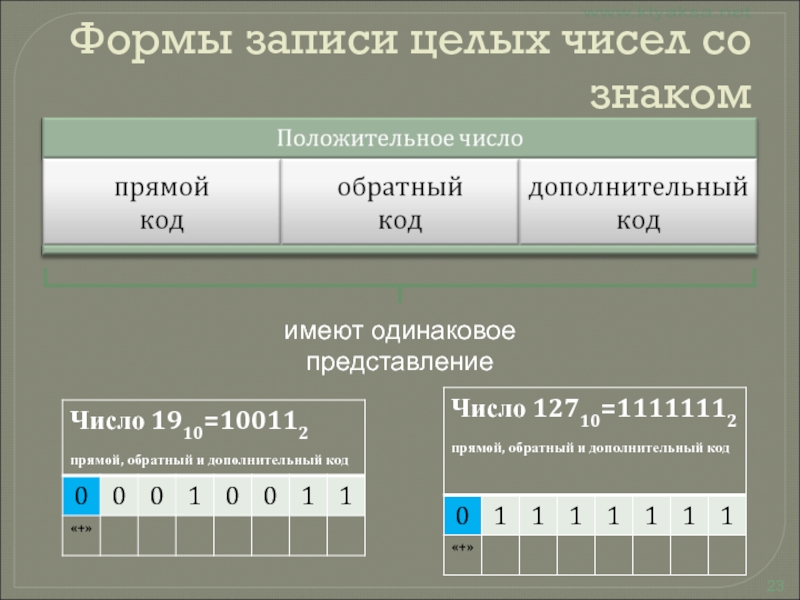
Слайд 22Формы записи целых чисел со знаком
Слайд 23Формы записи целых чисел со знаком
имеют одинаковое представление
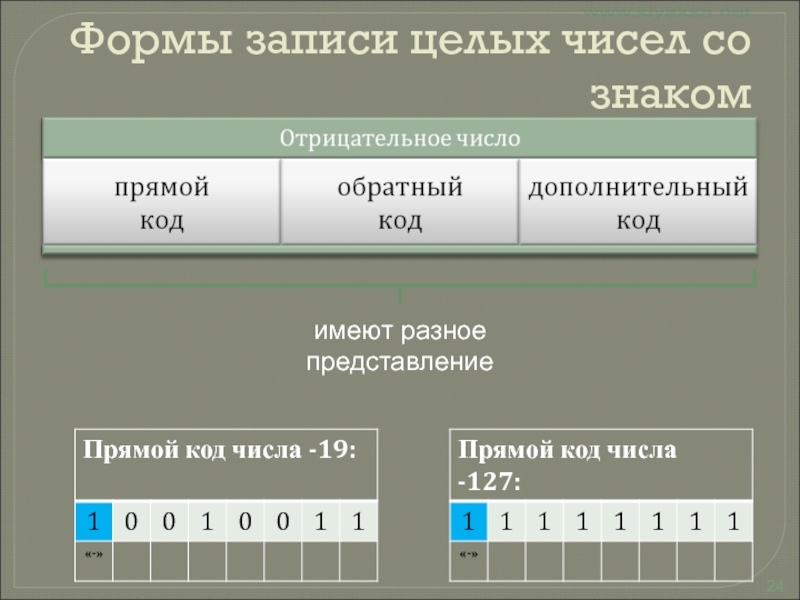
Слайд 24Формы записи целых чисел со знаком
имеют разное представление
Слайд 25Формы записи целых чисел со знаком
Обратный код получается инвертированием всех
цифр двоичного кода абсолютной величины числа, включая разряд знака: нули
заменяются единицами, а единицы – нулями.
Дополнительный код получается образованием обратного кода с последующим прибавлением единицы к его младшему разряду.
Слайд 27Арифметические действия
1) А и В положительные:
Слайд 28Арифметические действия
2) А – положительное, В – отрицательное, |B|>|A|
При
переводе в прямой код биты цифровой части результата инвертируются и
к младшему разряду прибавляется единица: 10000110 + 1 = 10000111= -710
Слайд 29Арифметические действия
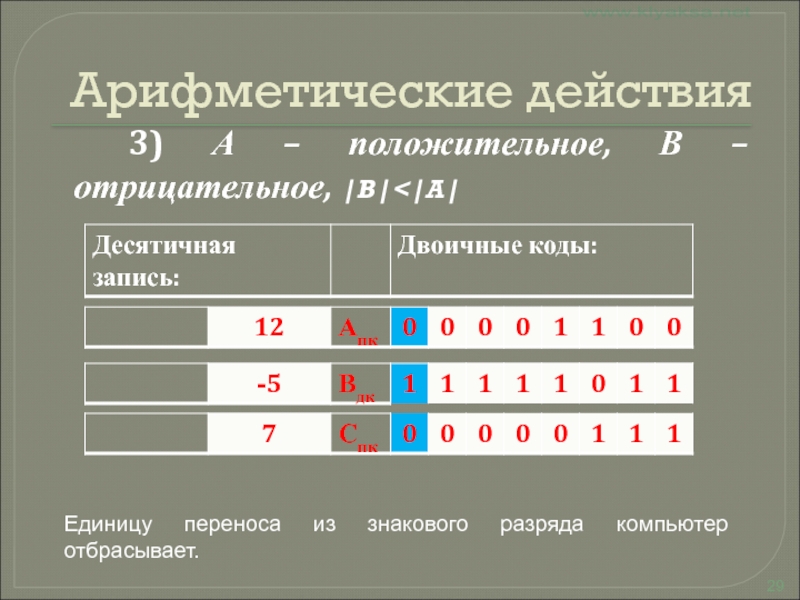
3) А – положительное, В – отрицательное, |B|
переноса из знакового разряда компьютер отбрасывает.
Слайд 30Арифметические действия
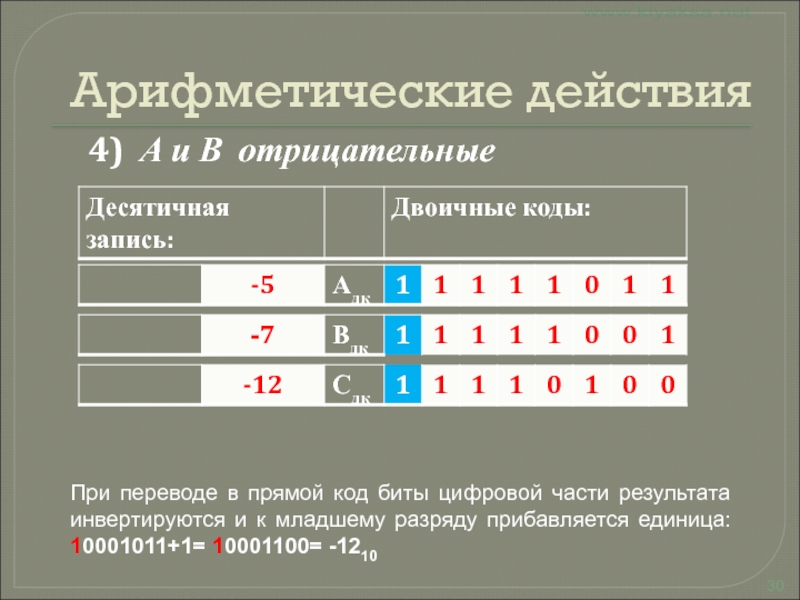
4) А и В отрицательные
При переводе в прямой код
биты цифровой части результата инвертируются и к младшему разряду прибавляется
единица: 10001011+1= 10001100= -1210