Слайд 1Представлення кількісних даних
Для аналізу та інтерпретації кількісних даних необхідно їх
узагальнити. Перший етап представлення - це упорядкування даних по величині
від максимальної до мінімальної.
Таке уявлення називають незгрупований ряд.
Група дітей шестирічного віку була протестована за методикою Керна-Йерасіка (тест на шкільну зрілість). Результати тестування з вербальної шкалою занесені в таблицю.
Впорядкуємо ряд даних за зменшенням:
15, 14, 14, 14, 14, 13, 13, 13, 13, 13, 13, 13, 13, 12, 12, 9
- це незгрупований ряд данных.
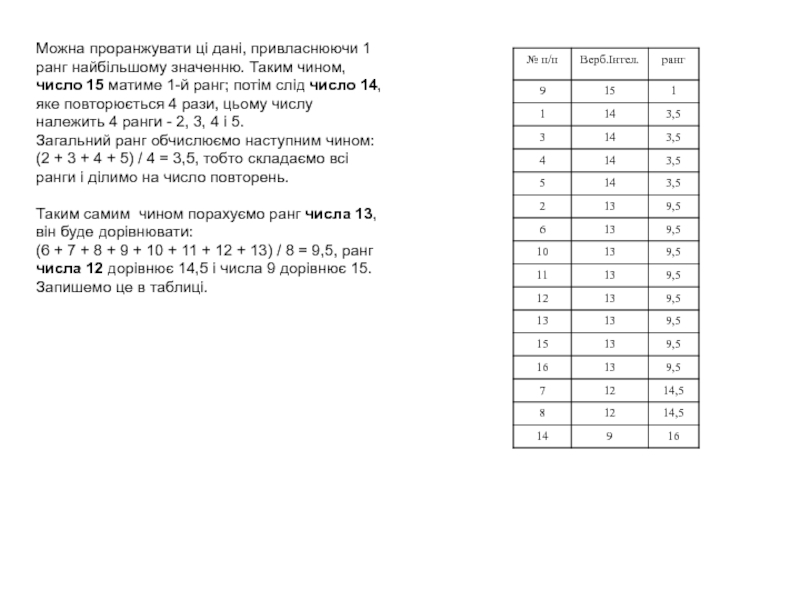
Слайд 2Можна проранжувати ці дані, привласнюючи 1 ранг найбільшому значенню. Таким
чином, число 15 матиме 1-й ранг; потім слід число 14,
яке повторюється 4 рази, цьому числу належить 4 ранги - 2, 3, 4 і 5.
Загальний ранг обчислюємо наступним чином: (2 + 3 + 4 + 5) / 4 = 3,5, тобто складаємо всі ранги і ділимо на число повторень.
Таким самим чином порахуємо ранг числа 13, він буде дорівнювати:
(6 + 7 + 8 + 9 + 10 + 11 + 12 + 13) / 8 = 9,5, ранг числа 12 дорівнює 14,5 і числа 9 дорівнює 15. Запишемо це в таблиці.
Слайд 3Цей список можна скоротити, класифікуючи оцінки з розподілу частот, іноді
званого просто розподілом.
У таблиці різні показники вербального інтелекту розміщуються
за величиною в даному випадку від 15 до 9, а праворуч від кожної оцінки вказується число її повторень.
Кожне число праворуч називається частотою і позначається f, сума частот позначається n.
Однак, цим аналіз розподілу даних ознаки не обмежується, оскільки частотний розподіл нічого не говорить про статистичні закономірності, які описували б числові характеристики досліджуваної сукупності.
До характеристик розподілу, що описує кількісно його структуру і будову, відносяться:
• міри центральної тенденції;
• міри розсіювання;
• показники асиметрії та ексцесу.
Слайд 4До характеристик оцінки центральної тенденції належать:
мода (Мо), медіана (Мd),
квантилі і середнє арифметичне (M).
Ме Хср.;
Важливе значення має така величина ознаки, яка зустрічається найчастіше в досліджуваному ряді (в сукупності).
Така величина називається модою (Мо). В дискретному ряді Мо визначається без обчислення, як значення ознаки з найбільшою частотою
(наприклад, за даними таблиці Мо = 13).
При розрахунку моди може виникнути кілька ситуацій:
1. Два значення ознаки, що стоять поруч, зустрічаються однаково часто. В цьому випадку
мода дорівнює середньому арифметичному цих двох значень. Наприклад, в наступному ряду даних:
12, 13, 14, 14, 14, 16, 16, 16, 18, 19
Мо = (14 + 16) / 2 = 15.
2. Два значення, зустрічаються також однаково часто, але не стоять поруч. В цьому випадку
кажуть, що ряд даних має дві моди, тобто він бімодальний.
3. Якщо всі значення даних зустрічаються однаково часто, то кажуть, що ряд не має
моди.
Найчастіше зустрічаються ряди даних з одним модальним значенням ознаки.
Слайд 5Бімодальність розподілу дає важливу інформацію про природу досліджуваної змінної. Наприклад,
якщо змінна являє собою перевагу або ставлення до чогось, то
бімодальність може означати протилежність думок.
Бімодальність часто може показувати, що вибірка не є однорідною і спостереження породжені двома або більше "накладеними" розподілами.
Іноді бімодальність розподілу означає, що обрані інструменти не підходять для вимірювання (наприклад "проблеми розмітки" в природничих науках, "зміщені відповіді" в соціальних).
Слайд 6Приклад 1. Вiдома класифiкацiя психологiчних типiв людини визначає чотири iдеальних
характери: сангвiнiк, холерик, меланхолiк та флегматик.
Припустимо, маємо тест з
40 питань для аналiзу характеру людини за наведеною класифiкацiєю. Нехай на кожне питання є чотири варiанти вiдповiдi, причому кожний варiант вiдповiдає одному з типiв.
Нехай за цiєю методикою опитано деяку людину. Припустимо,
6 з ї ї вiдповiдей зараховано до типу “сангвiнiк” ,
8 — “холерик”,
3 — “меланхолiк” ,
23 — “флегматик” .
Тодi модою цих даних є тип “флегматик” , позаяк вiн найчастiше зустрiчається у вiдповiдях. Отже, цей тип переважає в характерi опитаного.
Зауважимо також, що розглянуто данi, якi вимiрюються за номiнальною шкалою. Отже, моду можна застосовувати навiть для аналiзу нечислових значень.
Слайд 7Приклад 2. Розглянемо результати соцiологiчного дослiдження, здiйсненого з метою встановлення
середньої кiлькостi дiтей у сiм’ї. Загалом було опитано 84 сiм’ї.
Наведемо результати опитування.
Чому дорівнює мода??
Слайд 8Друга числова характеристика ряду даних називається медіаною (Ме) - це
таке значення ознаки, яке ділить ряд навпіл.
Інакше, медіана володіє
тиєю властивістю, що половина всіх вибіркових значень ознаки менше неї, половина більше.
При непарному числі елементів в ряду даних, медіана дорівнює центральному члену ряду, а при парному- середньому арифметичному двох центральних значень ряду.
У нашому прикладі Ме = (13 + 13) / 2 = 13.
Обчислення медіани має сенс тільки для порядкового ознаки.
Слайд 9Приклад 3. Нехай у результатi тестування вiдомi IQ-iндекси шiстьох спiвробiтникiв
вiддiлу маркетингу компанiї (через анонiмнiсть не вказано посади спiвробiтникiв).
Визначимо медiану
цих значень. Для цього, упорядкувавши список, отримаємо таку послiдовнiсть IQ-iндексiв:
124; 128; 131; 132; 140; 142
Оскiльки кiлькiсть значень у групi парна (6 iндексiв), для визначення медiани потрiбно розглянути два числа, якi мiстяться посерединi списку — 131 та 132.
Отже, обчислюємо медiану:
Слайд 10Квантіль - це таке значення ознаки, яке ділить розподілення у
заданій пропорції: зліва 0,5%, праворуч 99,5%; зліва 2,5%, праворуч 97,5%
і т.п.
Зазвичай виділяють такі різновиди квантилів:
1) квартіль Q1, Q 2, Q3 - вони ділять розподіл на чотири частини за 25% у кожній;
2) квінтіль K1, К2, К3, К4- вони ділять розподіл на п'ять частин за 20% у кожній;
3) дециль D1, ..., D9, їх дев'ять, і вони ділять розподіл на десять частин за 10% у кожній;
4) процентиль P1, Р2 ..., Р99, їх дев'яносто дев'ять, і вони ділять розподіл на сто частин за 1% у кожній частині.
Слайд 11Середнє арифметичне значення ознаки, обчислене для якої-небудь групи, інтерпретується як
значення найбільш типове для цієї групи (людини). Однак бувають випадки,
коли подібна інтерпретація неспроможна (у випадку, якщо існує велика різниця між мінімальним і максимальним значеннями ознаки).
Середнє арифметичне значення ознаки:
Нехай аналiзується сукупнiсть статистичних даних, яка складається з n чисел
X1; X2; Х3; Х4 : : : ;Xn.
Середнє арифметичне цих чисел визначають так
Слайд 12Приклад 4. Нехай студенти деякої академiчної групи отримали такi оцiнки
на екзаменi:
Тодi середнє значення оцiнки (iншими словами, середня оцiнка)
групи
Однак бувають
випадки, коли подібна інтерпретація неправомірна (у випадку, якщо існує велика різниця між мінімальним і максимальним значеннями ознаки).
Приклад 5. Нехай дослiджується середнiй заробiток програмiста в Києвi. Для цього було здiйснено Internet-опитування. Нехай 8 програмiстiв анонiмно зазначили свiй середнiй щомiсячний заробiток (див. таблицю).
Слайд 13Порiвняння середнього значення, медiани та моди
Як було встановлено ранiше, середнє
значення, мода i медiана можуть рiзнитися навiть для однiєї й
тiєї самої сукупностi статистичних даних. Кожна з цих величин дає певну iнтерпретацiю поняття середнього: мода — щодо частоти появи значення, медiана — щодо середньої позицiї у впорядкованому списку даних, середнє значення враховує як частоту появи даних, так i їх значення. Природно постає питання, яка з цих характеристик краща.
Однозначної вiдповiдi не iснує.
Залежно вiд сукупностi даних будь-яка з цих величин може стати як найкращою, так i найгiршою усередненою характеристикою.
Приклад 6. Розглянемо сукупнiсть з шести осiб. Наведемо данi про їх сукупнi рiчнi прибутки.
За наведеними даними насамперед визначимо моду, медiану та середнє значення:
Mo = 200;
Me = (200 + 1250)/2 = 725;
Xср = (150 + 200 +200 + 1250 + 10000 + 1 000 000)/6 = 1 011 800
Слайд 14Характеристики розсіювання
Використовуючи для опису ряду значень ознаки, тільки міру
центральної тенденції, можна сильно помилитися в оцінці характеру досліджуваної сукупності.
Це добре видно на такому прикладі. Припустимо, ми вивчаємо середній вік в двох групах, що складаються кожна з 6-ти осіб.
Значення ознаки розподілилися наступним чином:
1 група - 10, 10, 10, 50, 50, 50
2 група - 30, 30, 30, 30, 30, 30
Підрахувавши середнє значення в кожній з груп, отримаємо
Хср1 = 30 і Хср2 = 30.
Тобто ми отримали однакові значення, тоді як цілком очевидно, що вибірки взяті з різних сукупностей. Помилка сталася через розкид значень віку в цих групах.
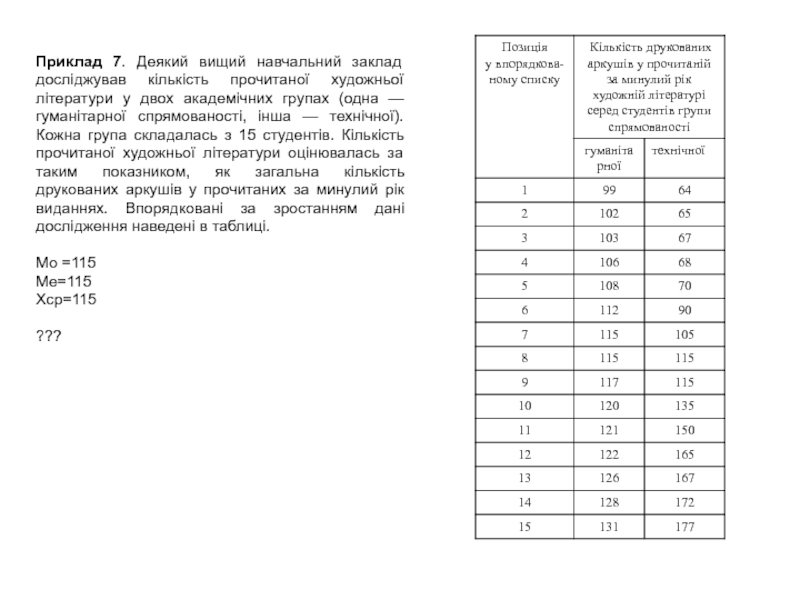
Слайд 15Приклад 7. Деякий вищий навчальний заклад дослiджував кiлькiсть прочитаної художньої
лiтератури у двох академiчних групах (одна — гуманiтарної спрямованостi, iнша
— технiчної). Кожна група складалась з 15 студентiв. Кiлькiсть прочитаної художньої лiтератури оцiнювалась за таким показником, як загальна кiлькiсть друкованих аркушiв у прочитаних за минулий рiк виданнях. Впорядкованi за зростанням данi дослiдження наведенi в таблицi.
Мо =115
Ме=115
Хср=115
???
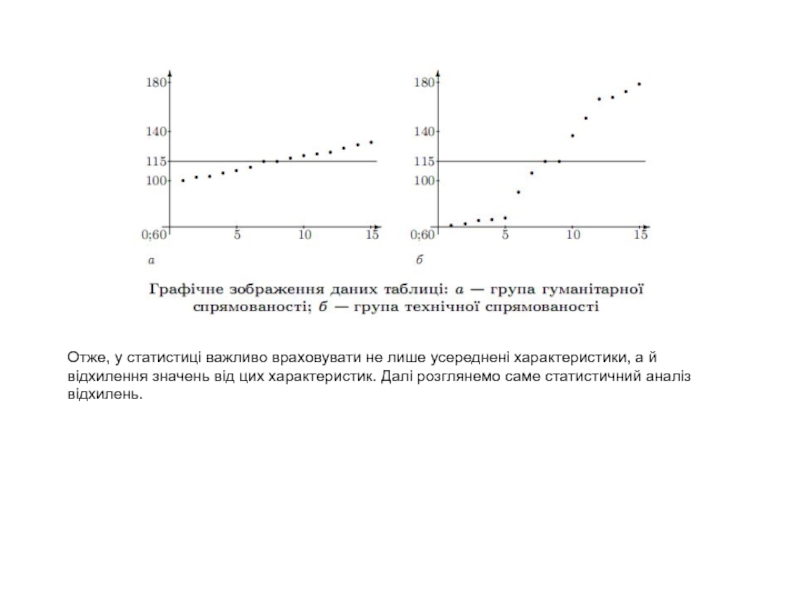
Слайд 16Отже, у статистицi важливо враховувати не лише усередненi характеристики, а
й вiдхилення значень вiд цих характеристик. Далi розглянемо саме статистичний
аналiз вiдхилень.
Слайд 17Розмах.
Найпростішою з таких мір є розмах R (або d)
- різниця між мінімальним і максимальним значенням випадкової величини в
даному розподілі.
Цілком очевидно, що два розподілу, що мають однакові середні арифметичні, медіану і моду можуть розрізнятися за розмахом, оскільки міри центральної тенденції не показують наскільки дані розкидані на числовій осі.
R = xmax - хmin.
Слайд 18У статистицi, дослiджуючи розсiювання даних, найчастiше використовують такi характеристики, як
середнє відхилення, стандартне вiдхилення i дисперсiю. Цi характеристики важливi завдяки
зручностi їх математичних перетворень, необхiдних у статистичному аналiзi.
Середнє відхилення являє собою відношення суми модулів центральних відхилень до числа спостережень і обчислюється за формулою:
Очевидно, що для двох різних розподілів, що характеризуються однаковими раніше описаними параметрами, середнє відхилення буде більше в тому випадку, якщо в розподілі частіше зустрічаються віддалені від середнього значення.
Середнє відхилення є корисною мірою розсіювання, однак використовується рідше, ніж дисперсія (σ або D) - відношення суми квадратів центральних відхилень до числа спостережень (n).
('' Байєсівський '' метод для обчислення дисперсії генеральної сукупності).
У тому випадку, якщо дослідник має справу не з генеральною сукупністю, а з вибіркою, формула дисперсії буде трохи інша - відношення суми квадратів центральних відхилень не до n, а до n-1 (т.зв. '' незміщена '' оцінка дисперсії) :
Слайд 19Стандартне відхилення являє собою корінь з дисперсії:
В описі психологічних
змінних, стандартне відхилення часто використовується як показник кордонів більшості значень
або умовної норми, що є особливо важливим в психології особистості, дослідженнях інтелекту і т.д.
В даний час практично всі важливі стандартизовані психодіагностичні шкали (шкала Т-балів, шкала стенов, шкала IQ і т.д.) створені з урахуванням стандартного відхилення.
Приклад 2.3.6. Знову повернiмося до прикладу про кiлькiсть художньої лiтератури, прочитаної за рiк студентами двох академiчних груп.
За отриманими даними обчислюємо дисперсiї (як середнє значення квадратiв абсолютних вiдхилень) i стандартнi вiдхилення (як квадратний корiнь з дисперсiї):
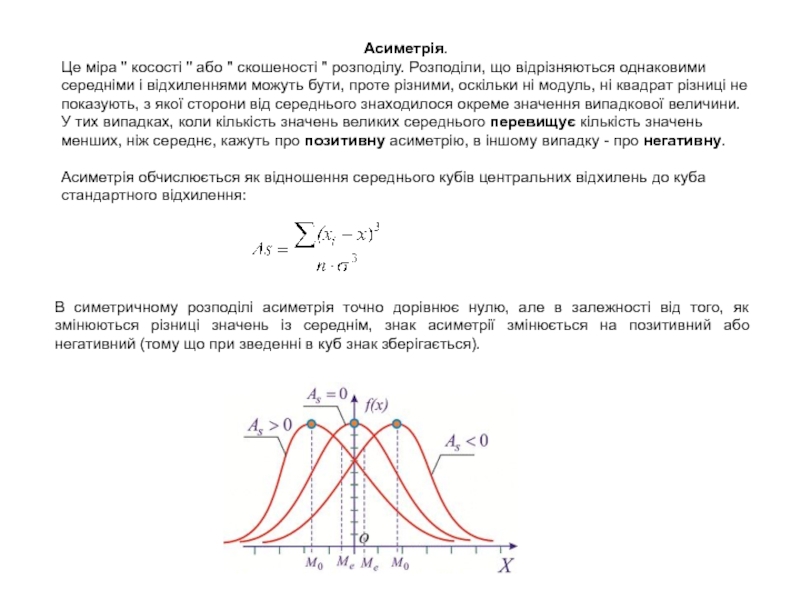
Слайд 20Асиметрія.
Це міра '' косості '' або '' скошеності ''
розподілу. Розподіли, що відрізняються однаковими середніми і відхиленнями можуть бути,
проте різними, оскільки ні модуль, ні квадрат різниці не показують, з якої сторони від середнього знаходилося окреме значення випадкової величини. У тих випадках, коли кількість значень великих середнього перевищує кількість значень менших, ніж середнє, кажуть про позитивну асиметрію, в іншому випадку - про негативну.
Асиметрія обчислюється як відношення середнього кубів центральних відхилень до куба стандартного відхилення:
В симетричному розподілі асиметрія точно дорівнює нулю, але в залежності від того, як змінюються різниці значень із середнім, знак асиметрії змінюється на позитивний або негативний (тому що при зведенні в куб знак зберігається).
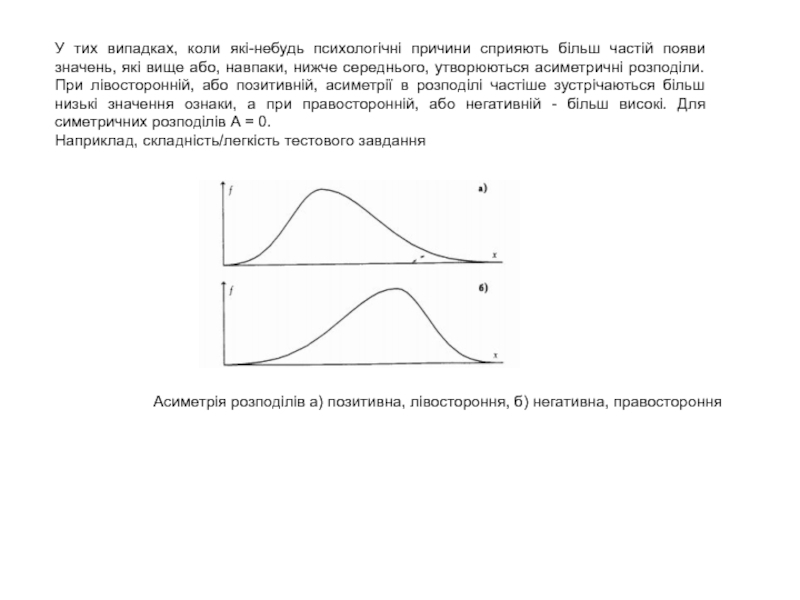
Слайд 21У тих випадках, коли які-небудь психологічні причини сприяють більш частій
появи значень, які вище або, навпаки, нижче середнього, утворюються асиметричні
розподіли. При лівосторонній, або позитивній, асиметрії в розподілі частіше зустрічаються більш низькі значення ознаки, а при правосторонній, або негативній - більш високі. Для симетричних розподілів А = 0.
Наприклад, складність/легкість тестового завдання
Асиметрія розподілів а) позитивна, лівостороння, б) негативна, правостороння
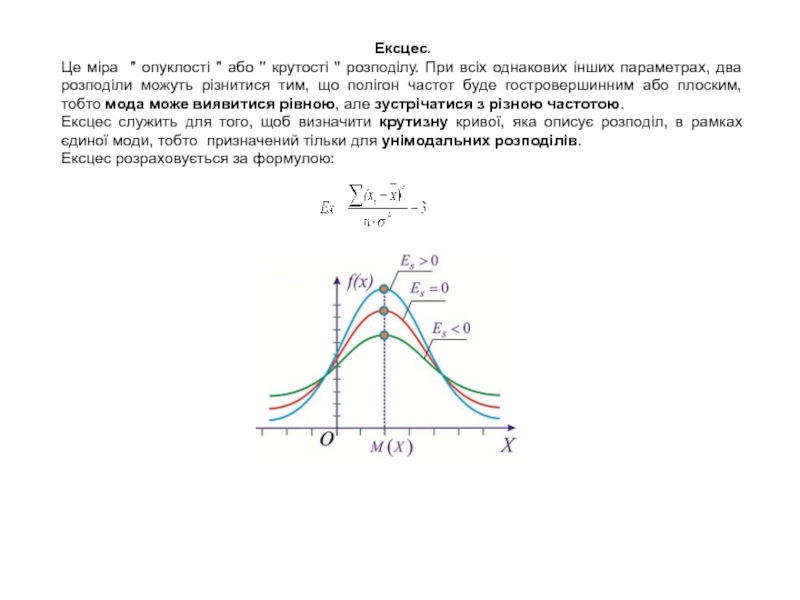
Слайд 22Ексцес.
Це міра '' опуклості '' або '' крутості ''
розподілу. При всіх однакових інших параметрах, два розподіли можуть різнитися
тим, що полігон частот буде гостровершинним або плоским, тобто мода може виявитися рівною, але зустрічатися з різною частотою.
Ексцес служить для того, щоб визначити крутизну кривої, яка описує розподіл, в рамках єдиної моди, тобто призначений тільки для унімодальних розподілів.
Ексцес розраховується за формулою:
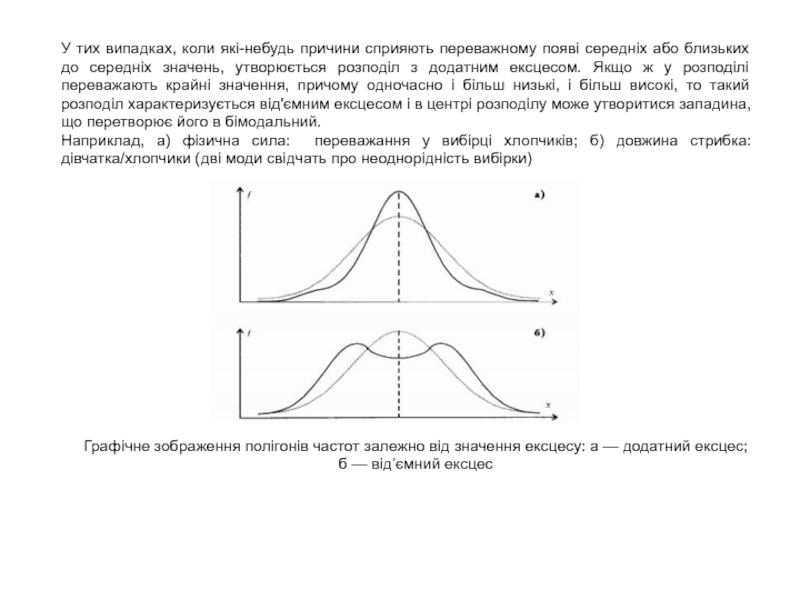
Слайд 23У тих випадках, коли які-небудь причини сприяють переважному появі середніх
або близьких до середніх значень, утворюється розподіл з додатним ексцесом.
Якщо ж у розподілі переважають крайні значення, причому одночасно і більш низькі, і більш високі, то такий розподіл характеризується від'ємним ексцесом і в центрі розподілу може утворитися западина, що перетворює його в бімодальний.
Наприклад, а) фізична сила: переважання у вибірці хлопчиків; б) довжина стрибка: дівчатка/хлопчики (дві моди свідчать про неоднорідність вибірки)
Графiчне зображення полiгонiв частот залежно вiд значення ексцесу: а — додатний ексцес;
б — вiд’ємний ексцес
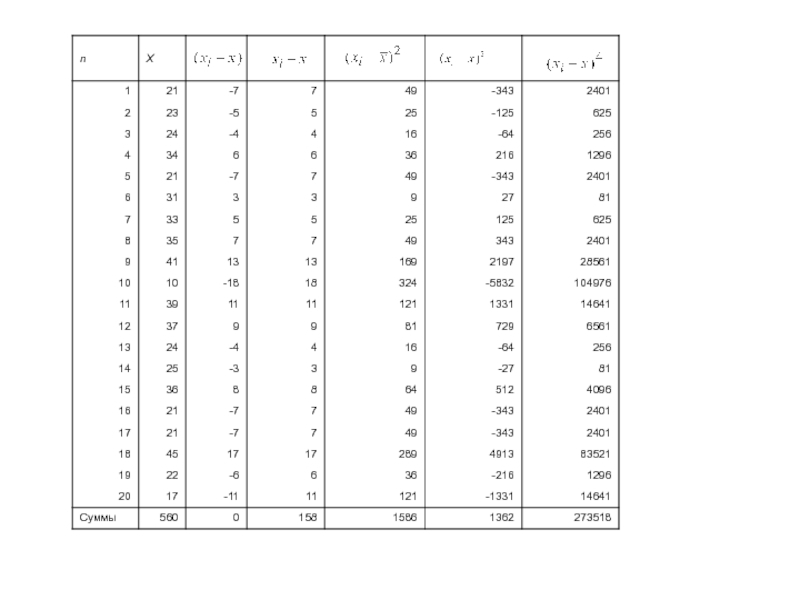
Слайд 25Розрахунок мір центральної тенденції та квартилей розподілу:
Md = 24.5
Mo = 21 Q1 = 21 Q2 =
24.5 Q3 = 35.5
Розрахунок мір розсіювання:
Щодо даного розподілу можна сказати, що:
Розподіл унімодальний;
Основна маса значень знаходиться в межах (одного стандартного відхилення) від 19 до 37, а 50% спостережень - від 21 до 35.5;
Він характеризується позитивною асиметрією, що означає, що більш виражені відхилення в більшу від середнього арифметичного сторону;
Розподіл "пологий" (негативний ексцес), тобто значення випадкової величини розподілені за числовий шкалою досить рівномірно.
Слайд 26Математичний ідеал: нормальний розподіл
В психологічних дослідженнях найчастіше посилаються на нормальний
розподіл.
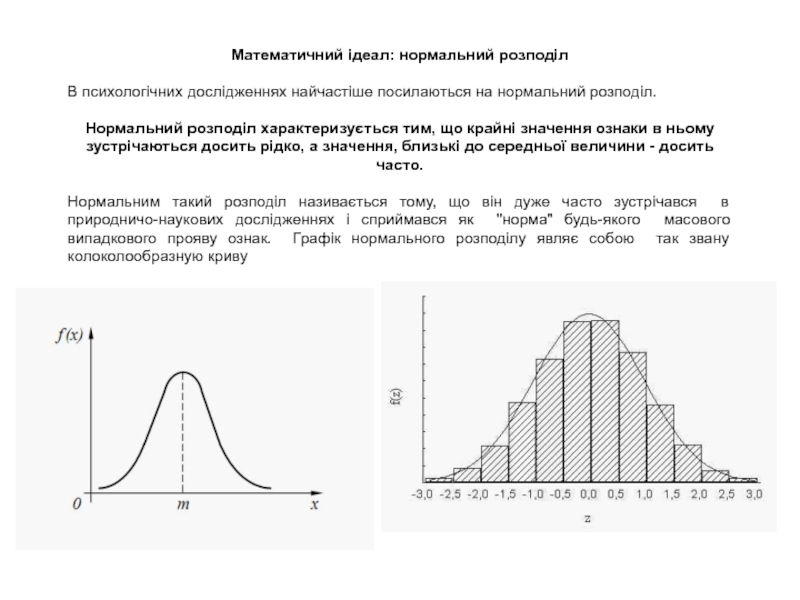
Нормальний розподіл характеризується тим, що крайні значення ознаки в
ньому зустрічаються досить рідко, а значення, близькі до середньої величини - досить часто.
Нормальним такий розподіл називається тому, що він дуже часто зустрічався в природничо-наукових дослідженнях і сприймався як "норма" будь-якого масового випадкового прояву ознак. Графік нормального розподілу являє собою так звану колоколообразную криву
Слайд 27Основна властивість нормального розподілу: значення моди, медіани і середнього
арифметичного
рівні між собою.
Хср =Мо=Мd
Другою важливою властивістю нормального розподілу є
наявність певної кількості
випадкової величини (випадків), яка потрапляє між значеннями
Хср – σ та Хср + σ,
(зазвичай цю кількість вимірюють у відсотках від загального числа випадків).
Вважається, що нормальний розподіл характеризує такі випадкові величини, на які впливає велика кількість різноманітних факторів, причому сила впливу одного окремо взятого фактора значно менше суми впливів інших чинників.
В результаті виходить, що найчастіше зустрічаютсья середні значення вимірюваного параметра, рідшими є крайні, і що сильніше відрізняється якесь значення від середнього, тим рідше воно зустрічається.
Психологи вважають, що більшість психологічних властивостей, якостей (інтелект, властивості особистості і т.п.) також має нормальний розподіл, саме з цієї посилки виходять при проведенні стандартизації тестових методик.
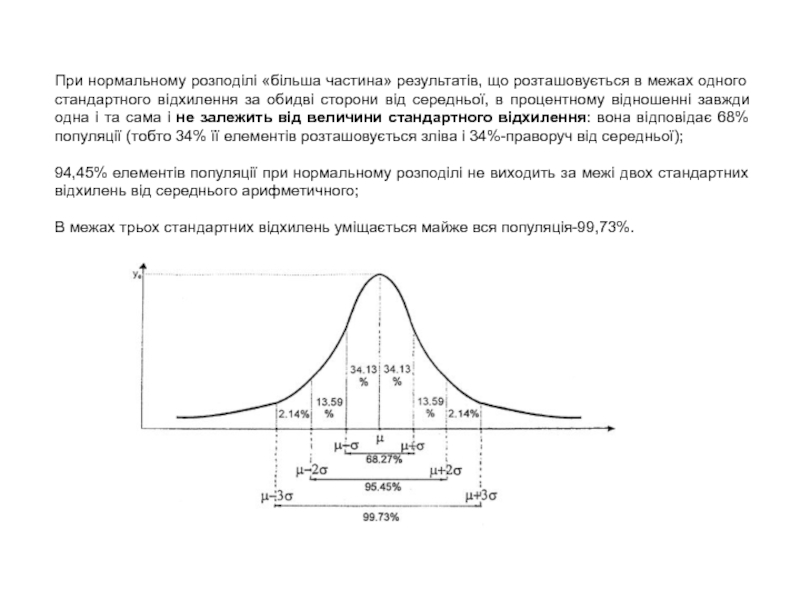
Слайд 28При нормальному розподілі «більша частина» результатів, що розташовується в межах
одного стандартного відхилення за обидві сторони від середньої, в процентному
відношенні завжди одна і та сама і не залежить від величини стандартного відхилення: вона відповідає 68% популяції (тобто 34% її елементів розташовується зліва і 34%-праворуч від середньої);
94,45% елементів популяції при нормальному розподілі не виходить за межі двох стандартних відхилень від середнього арифметичного;
В межах трьох стандартних відхилень уміщається майже вся популяція-99,73%.