Слайд 1Теория вероятностей возникла как наука из убеждения, что в основе
массовых случайных событий лежат детерминированные закономерности, теория вероятностей изучает эти
закономерности.
Математическая статистика это наука изучающая методы обработки результатов наблюдения массовых случайных явлений, обладающих статистической устойчивостью, с целью выявления этих закономерностей
Предмет теории вероятностей
Слайд 2 Развитие теории вероятностей с момента зарождения этой науки
и до настоящего времени было несколько своеобразным. На первом этапе
истории этой науки она рассматривалась как занимательный “пустячок”, как собрание курьезных задач, связанных в первую очередь с азартными играми в кости и карты.
История возникновения теории вероятностей
Слайд 3❶ Предыстория теории вероятностей.
В этот период, начало
которого теряется в веках, ставились и решались элементарные задачи, которые
позже будут отнесены к теории вероятностей. Никаких специальных методов в этот период не возникает. Этот период кончается работами Кардано, Пачоли, Тарталья и др. С вероятностными представлениями мы встречаемся еще в античности. У Демокрита, Лукреция Кара и других античных ученых и мыслителей мы находим глубокие предвидения о строении материи с беспорядочным движением мелких частиц (молекул), мы встречаем рассуждения о равновозможных исходах (равновероятных) и т. п.
Этапы развития
Н. Тарталья
Д. Кардано
Слайд 4❷ Возникновение теории вероятностей как науки.
К середине, XVII
в. вероятностные вопросы и проблемы, возникающие в статистической практике, в
практике страховых обществ, при обработке результатов наблюдений и в других областях, привлекли внимание ученых, так как они стали актуальными вопросами. В первую очередь это относится к Б. Паскалю, П. Ферма и X. Гюйгенсу. В этот период вырабатываются первые специфические понятия, такие, как математическое ожидание и вероятность (в форме отношения шансов), устанавливаются и используются первые свойства вероятности: теоремы сложения и умножения вероятностей. В это время теория вероятностей находит свои первые применения в демографии, страховом деле, в оценке ошибок наблюдения, широко используя при этом понятие вероятности.
Этапы развития
Слайд 5 Основателями теории вероятностей были французские математики Б. Паскаль и
П. Ферма, и голландский ученый Х. Гюйгенс
Основатели теории вероятностей
Б. Паскаль
П.Ферма
Х. Гюйгенс
Слайд 6❸ Классическое определение вероятности. Следующий период начинается с появления работы
Я. Бернулли "Искусство предположений" (1713), в которой впервые была строго
доказана первая предельная теорема — простейший случай закона больших чисел. К этому периоду, который продолжался до середины XIX в., относятся работы Муавра, Лапласа, Гаусса и др. В центре внимания в это время стоят предельные теоремы. Теория вероятностей начинает широко применяться в различных областях естествознания. И хотя в этот период начинают применяться различные понятия вероятности (геометрическая вероятность, статистическая вероятность), господствующее положение занимает, в особенности после работ Лапласа, так называемое классическое определение вероятности.
Этапы развития
Якоб
Бернулли
Слайд 7❹ Следующий период развития теории вероятностей связан прежде всего с
Петербургской математической школой. За два столетия развития теории вероятностей главными
ее достижениями были предельные теоремы. Но не были выяснены границы их применимости и возможности дальнейшего обобщения. Наряду с огромными успехами, достигнутыми теорией вероятностей в предыдущий период, были выявлены и существенные недостатки в ее обосновании, это в большой мере относится к недостаточно четким представлениям о вероятности.
Этапы развития.
Слайд 8❺ Современный период развития теории вероятностей начался с установления аксиоматики.
Этого прежде всего требовала практика, так как для успешного применения
теории вероятностей в физике, биологии и других областях науки, а также в технике и военном деле необходимо было уточнить и привести в стройную систему ее основные понятия. Благодаря аксиоматике теория вероятностей стала абстрактно-дедуктивной математической дисциплиной, тесно связанной с другими математическими дисциплинами. Это обусловило небывалую широту исследований по теории вероятностей и ее применениям, начиная от хозяйственно-прикладных вопросов и кончая самыми тонкими теоретическими вопросами теории информации и теории случайных процессов.
Этапы развития
Слайд 9 Строгое логическое обоснование теории вероятностей произошло в XX
в. и связано с именами советских математиков С. Н. Бернштейна и А. Н. Колмогорова.
Основатели
теории вероятностей
С. Н. Бернштейн
А. Н. Колмогоров
Слайд 10 Возникновение и развитие теории вероятностей продиктовано необходимостью ее применениям, начиная
от хозяйственно-прикладных вопросов и заканчивая самыми тонкими теоретическими вопросами теории
информации и теории случайных процессов.
Выводы:
Слайд 11ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ ВЕРОЯТНОСТИ
Слайд 13 Под СОБЫТИЕМ понимается явление, которое происходит
в результате осуществления какого-либо определенного комплекса условий.
ПРИМЕР. Бросаем шестигранный игральный кубик.
Определим события:
А {выпало четное число очков};
В {выпало число очков, кратное 3};
С {выпало более 4 очкков}.
СОБЫТИЕ
✔
Слайд 14 ЭКСПЕРИМЕНТ (или опыт) заключается в наблюдении за объектами
или явлениями в строго определенных условиях и измерении значений заранее
определенных признаков этих объектов (явлений).
Эксперимент(опыт)
✔
Слайд 15сдача экзамена,
наблюдение за дорожно-транспортными происшествиями,
выстрел из винтовки,
бросание
игрального кубика,
химический эксперимент,
и т.п.
ПРИМЕРЫ
Слайд 16 Эксперимент называют СТАТИСТИЧЕСКИМ, если он может быть повторен
в практически неизменных условиях неограниченное число раз.
СТАТИСТИЧЕСКИЙ
✔
Слайд 17 СЛУЧАЙНЫМ называют событие, которое может произойти или не
произойти в результате некоторого испытания (опыта). Обозначают заглавными буквами А,
В, С, Д,… (латинского алфавита).
СЛУЧАЙНОЕ СОБЫТИЕ
✔
Слайд 18Рассмотрим несколько наиболее «излюбленных» в теории вероятностей примеров случайных экспериментов.
Слайд 19 Подбрасывание монеты.
Испытание – подбрасывание монеты;
события – монета упала «орлом» или «решкой».
Опыт 1:
✔
«решка»
- лицевая сторона монеты (аверс)
«орел» - обратная сторона монеты (реверс)
Слайд 20 Подбрасывание кубика.
Это следующий по популярности
после монеты случайный эксперимент.
Испытание – подбрасывание кубика; события
– выпало 1, 2, 3, 4, 5 или 6 очков (и другие).
Опыт 2:
✔
Слайд 21 Выбор перчаток. В коробке лежат 3 пары одинаковых
перчаток. Из нее, не глядя, вынимаются две перчатки.
«Завтра
днем – ясная погода».
Здесь наступление дня – испытание, ясная погода – событие.
Опыт 3:
✔
✔
Опыт 4:
Слайд 22Типы событий
ДОСТОВЕРНОЕ
НЕВОЗМОЖНОЕ
СЛУЧАЙНОЕ
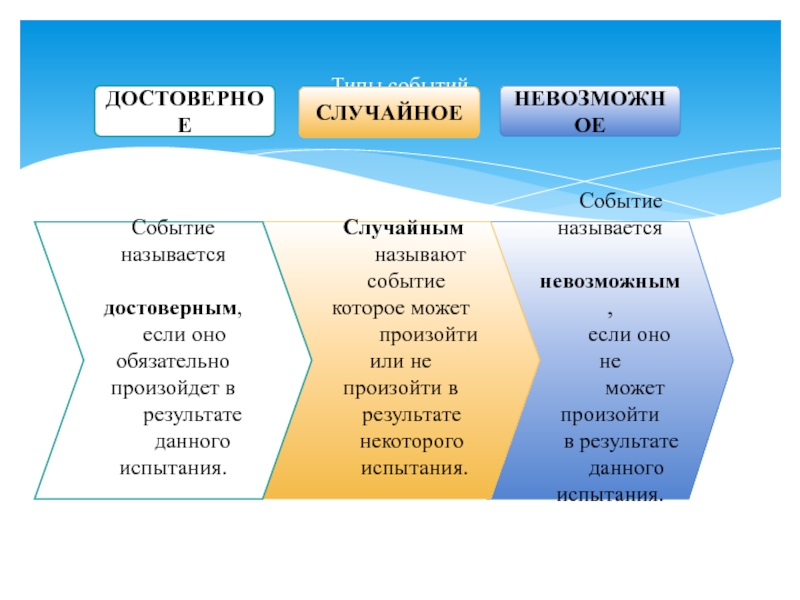
Слайд 23Типы событий
Событие называется
невозможным,
если оно не
может произойти
в результате
данного испытания.
Случайным
называют
событие которое может
произойти или не произойти в
результате
некоторого
испытания.
Событие
называется
достоверным,
если оно обязательно произойдет в
результате
данного испытания.
ДОСТОВЕРНОЕ
СЛУЧАЙНОЕ
НЕВОЗМОЖНОЕ
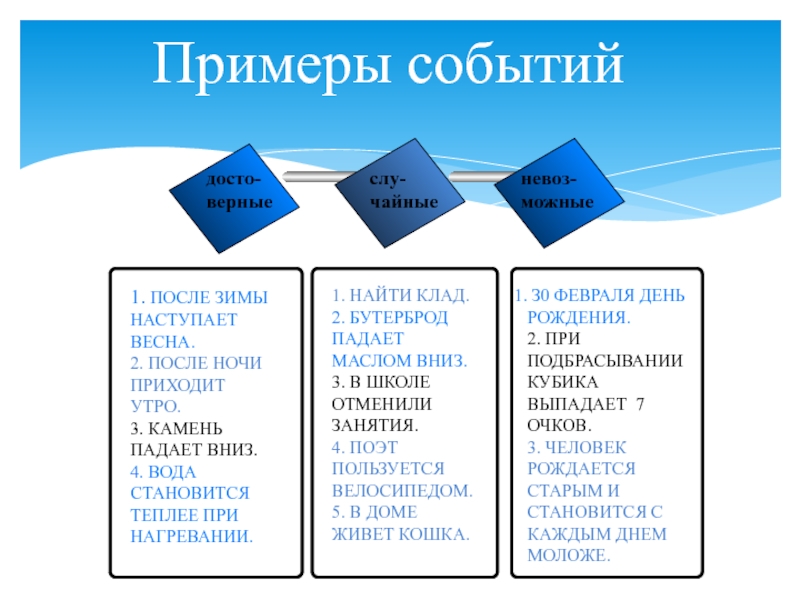
Слайд 24Примеры событий
досто-
верные
слу-
чайные
невоз-
можные
1. ПОСЛЕ ЗИМЫ НАСТУПАЕТ ВЕСНА.
2. ПОСЛЕ НОЧИ ПРИХОДИТ УТРО.
3.
КАМЕНЬ ПАДАЕТ ВНИЗ.
4. ВОДА СТАНОВИТСЯ ТЕПЛЕЕ ПРИ НАГРЕВАНИИ.
1. НАЙТИ
КЛАД.
2. БУТЕРБРОД ПАДАЕТ МАСЛОМ ВНИЗ.
3. В ШКОЛЕ ОТМЕНИЛИ ЗАНЯТИЯ.
4. ПОЭТ ПОЛЬЗУЕТСЯ ВЕЛОСИПЕДОМ.
5. В ДОМЕ ЖИВЕТ КОШКА.
З0 ФЕВРАЛЯ ДЕНЬ РОЖДЕНИЯ.
2. ПРИ ПОДБРАСЫВАНИИ КУБИКА ВЫПАДАЕТ 7 ОЧКОВ.
3. ЧЕЛОВЕК РОЖДАЕТСЯ СТАРЫМ И СТАНОВИТСЯ С КАЖДЫМ ДНЕМ МОЛОЖЕ.
Слайд 25Охарактеризуйте события, о которых идет речь в приведенных заданиях как
достоверные, невозможные или случайные.
Петя задумал натуральное число. Событие состоит в
следующем:
а) задумано четное число;
б) задумано нечетное число;
в) задумано число, не являющееся ни четным, ни нечетным;
г) задумано число, являющееся четным или нечетным.
Задание 1
Слайд 26Задание 2
В мешках лежит 10 шаров: 3 синих, 3
белых и 4 красных.
Охарактеризуйте следующее событие:
а) из мешка вынули
4 шара и они все синие;
б) из мешка вынули 4 шара и они все красные;
в) из мешка вынули 4 шара, и все они оказались разного цвета;
г) из мешка вынули 4 шара, и среди них не оказалось шара черного
цвета.
Слайд 28 ИСХОДОМ (или элементарным исходом, элементарным событием) называется
один из взаимоисключающих друг друга вариантов, которым может завершиться случайный
эксперимент.
ИСХОД
✔
Слайд 29 Опыт 1. – 2 исхода: «орел», «решка».
Опыт 2. – 6 исходов: 1, 2, 3, 4, 5,
6.
Опыт 3. – 3 исхода: «обе перчатки на левую руку», «обе перчатки на правую руку», «перчатки на разные руки».
Число возможных исходов в каждом из рассмотренных выше опытах.
✔
✔
✔
Слайд 30Однозначные исходы предполагают единственный результат того или иного события: смена
дня и ночи, смена времени года и т.д.
Слайд 31Неоднозначные исходы предполагают несколько различных результатов того или иного события:
при подбрасывании кубика выпадают разные грани; выигрыш в Спортлото; результаты
спортивных игр.
Слайд 32Запишите множество исходов для следующих испытаний.
а) В урне четыре шара
с номерами два, три, пять, восемь. Из урны наугад извлекают
один шар.
б) В копилке лежат три монеты достоинством в 1 рубль, 2 рубля и 5 рублей. Из копилки достают одну монету.
в) В доме девять этажей. Лифт находится на первом этаже. Кто-то из жильцов дома вызывает лифт на свой этаж. Лифтовый диспетчер наблюдает, на каком этаже лифт остановится.
Задание 3
Слайд 33Задание 4
Найдите количество возможных исходов.
а) За городом N
железнодорожные станции расположены в следующем порядке: Луговая, Сосновая, Озёрная, Дачная,
Пустырь. Событие А – пассажир купил билет не далее станции Озёрная.
б) Один ученик записал целое число от 1 до 5, а другой ученик пытается отгадать это число. Событие В – записано чётное число.
в) Вини Пух думает, к кому бы пойти в гости: к Кролику, Пяточку, ослику Иа-Иа или Сове? Событие А – Вини Пух пойдёт к Пяточку; событие В – Вини Пух не пойдёт к Кролику.
Слайд 34Задание 5
В каждом из следующих опытов найдите количество возможных
исходов:
а) подбрасывание двух монет;
б) подбрасывание двух кнопок;
в) подбрасывание двух кубиков;
г)
подбрасывание монеты и кубика;
д) подбрасывание монеты, кнопки и кубика.
Слайд 35ТЕСТ
«Случайные исходы, события, испытания».
Слайд 361. О каком событии идёт речь? «Из 25
учащихся класса
двое справляют
день рождения 30 февраля».
А) достоверное; В) невозможное;
С) случайное
событие является
случайным:
А) слово начинается с буквы«ь»;
В) ученику 9 класса 14 месяцев;
С) бросили две игральные
кости: сумма выпавших на
них очков равна 8.
Слайд 38 3. Найдите достоверное
событие:
А) На уроке математики ученики
делали физические упражнения;
В) Сборная России по футболу не
станет чемпионом мира 2005 года;
С) Подкинули монету и она упала
на «Орла».
Слайд 39 4. Среди пар событий, найдите
несовместимые.
А)
В сыгранной Катей и Славой
партии шахмат, Катя проиграла и
Слава проиграл.
В) Из набора домино вынута одна
костяшка, на ней одно число очков больше 3, другое число 5.
С) Наступило лето, на небе ни облачка.
Слайд 405.Охарактеризуйте случайное
событие:
«новая электролампа не загорится».
Это
событие:
А) менее вероятно ;
В) равновероятное ;
С) более вероятное.
Слайд 41 6. Какие события из
перечисленных ниже являются
противоположными? В колоде
карт
лежат четыре туза и четыре короля
разных мастей. Достают карту наугад. Событие:
А) достанут трефового туза;
В) достанут туза любой масти;
С) достанут любую карту кроме
трефового туза.
Слайд 427. Колобок катится по лесным тропкам
куда глаза глядят. На полянке
его
тропинка расходится на четыре тропинки,
в конце которых Колобка
поджидают
Заяц, Волк, Медведь и Лиса. Сколько
исходов для выбора Колобком наугад
одной из четырёх тропинок.
А) 1; В) 4; С) 5.
Слайд 438. Два стрелка делают по одному
выстрелу в мишень. Сколько
исходов двух совместных
выстрелов?
А) 4;
В) 3; С) 2.
Слайд 449. Два шахматиста играют подряд
две партии. Сколько исходов у
этого события?
А) 4;
В) 2; С) 9.
Слайд 4510*. Случайный опыт состоит в
выяснении пола детей в семьях с
тремя
детьми. Сколько возможных
исходов у этого опыта?
А) 8;
В) 9; С) 6.
Слайд 47В толковом словаре С.И. Ожегова и Н.Ю. Шведовой:
«Вероятность – возможность
исполнения, осуществимости чего-нибудь».
Основатель современной теории вероятностей А.Н.Колмогоров:
«Вероятность математическая – это
числовая характеристика степени возможности появления какого-либо определенного события в тех или иных определенных, могущих повторяться неограниченное число раз условиях».
Слайд 48 Известно, по крайней мере, шесть основных схем определения
и понимания вероятности. Не все они в равной мере используются
на практике и в теории, но, тем не менее, все они имеют за собой разработанную логическую базу и имеют право на существование.
Понятие вероятности
Слайд 49КЛАССИЧЕСКОЕ
СТАТИСТИЧЕСКОЕ
ГЕОМЕТРИЧЕСКОЕ
ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
Слайд 50 КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ
Слайд 51ВЕРОЯТНОСТЬ
– ЭТО ЧИСЛЕННАЯ МЕРА ОБЪЕКТИВНОЙ ВОЗМОЖНОСТИ ПОЯВЛЕНИЯ СЛУЧАЙНОГО СОБЫТИЯ.
ТЕОРИЯ
ВЕРОЯТНОСТЕЙ ДАЕТ СПОСОБ НАХОЖДЕНИЯ ЧИСЛЕННОГО ЗНАЧЕНИЯ ВЕРОЯТНОСТИ СОБЫТИЯ:
А
– некоторое событие,
m – количество исходов, при которых событие А появляется,
n – конечное число равновозможных исходов.
P – обозначение происходит от первой буквы французского слова probabilite – вероятность.
Слайд 52 Вероятностью Р наступления случайного события А называется отношение
, где n – число всех возможных исходов эксперимента,
а m – число всех благоприятных исходов:
КЛАССИЧЕСКОЕ ОПРЕДЕЛЕНИЕ ВЕРОЯТНОСТИ.
Слайд 53
Пьер-Симо́н Лапла́с
Классическое определение вероятности было впервые дано в работах
французского математика Лапласа.
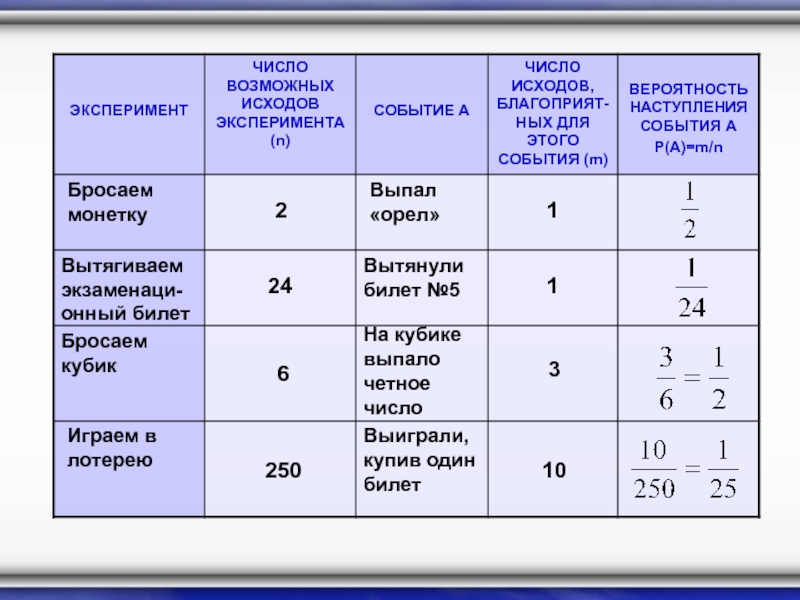
Слайд 54Бросаем монетку
2
Выпал «орел»
1
Вытягиваем экзаменаци- онный билет
Вытянули билет №5
24
1
Бросаем кубик
На кубике
выпало четное число
6
3
Играем в лотерею
Выиграли, купив один билет
250
10
Слайд 55Пример 1
В школе 1300 человек, из
них 5 человек хулиганы.
Какова вероятность того, что один из них попадётся директору на глаза?
Слайд 56Вероятность:
P(A) = 5/1300 = 1/250.
Решение
Слайд 57 При игре в нарды бросают 2 игральных кубика. Какова
вероятность того, что на обоих кубиках выпадут одинаковые числа?
Пример 2
Слайд 58Решение
Составим следующую таблицу
Вероятность: P(A)=6/36= =1/6.
Слайд 59
Пример 3.
Из карточек составили слово «статистика». Какую карточку с буквой
вероятнее всего вытащить? Какие события равновероятные?
с
т
а
т
и
с
т
и
к
а
Слайд 60Всего 10 букв.
Буква «с» встречается 2 раза –
P(с) =
2/10 = 1/5;
буква «т» встречается 3 раза –
P(т) =
3/10;
буква «а» встречается 2 раза –
P(а) = 2/10 = 1/5;
буква «и» встречается 2 раза –
P(и) = 2/10 = 1/5;
буква «к» встречается 1 раз –
P(к) = 1/10.
Решение
Слайд 62Вероятность достоверного события равна
Вероятность невозможного события равна
Вероятность события
А не меньше , но не больше
?
1
?
?
?
0
1
0
Слайд 63P(u) = 1 (u – достоверное событие);
P(v) = 0 (v
– невозможное событие);
0 ≤ P(A) ≤ 1.
Слайд 64
Основные элементы комбинаторики.
Размещение
Это любое упорядоченное подмножество m из элементов множества n.
(Порядок важен).
2. Перестановки
Если m = n, то эти размещения называются перестановками.
Сочетания
Это любое подмножество из m – элементов, которые принадлежат множеству, состоящему из n – различных элементов.
(Порядок не важен).
Следствие. Число сочетаний из n элементов по n – m равно число
сочетаний из n элементов по m, т.е.
Слайд 65
Задача.1.
Сколько можно записать четырехзначных чисел,
используя без повторения все
10 цифр?
Решение:
.
2) Т.к. есть среди чисел 0, который не может стоять впереди, поэтому надо еще найти:
3) .
Основные элементы комбинаторики.
Слайд 66
Решение задач.
Задача.2.
Пусть имеется множество, содержащие 4 буквы:
{А,В,С,Д}. Записать
все возможные сочетания из
указанных букв по три.
Решение:
Здесь
в число сочетаний не включены, например АВС,
ВСА, т.к. у нас уже есть АВС, потому что порядок
элементов в сочетании не учитываются.
Основные элементы комбинаторики.
Слайд 67
Решение задач.
Задача.3.
Сколькими способами можно расставить 9 различных книг
на полке,
чтобы определенные 4 книги стояли рядом?
Решение:
Если обозначить 4 определенные
книги как одно целое, то получается 6 книг, которые можно переставлять
способами.
4 определенные книги можно переставлять
способами.
Тогда всего перестановок по правилу умножения будет
Основные элементы комбинаторики.
Слайд 68
Решение задач.
Задача.4.
Нужно выбрать в подарок 4 из 10 имеющихся
книг.
Сколькими способами это можно сделать?
Решение:
Задача.5.
Имеется 10 белых
и 5 черных шаров. Сколькими
способами можно выбрать 7 шаров, чтобы среди них были
3 черных?
Решение: Белые шары: .
Черные шары: . Тогда .
Основные элементы комбинаторики.
Слайд 69
Решение задач.
Задача.6.
Сколькими способами можно группу из 12 человек
разбить
на 2 подгруппы, в одной из которых должно быть
не
более 5, а во второй – не более 9 человек?
Решение:
Первая подгруппа может состоять либо из 3, либо из 4,
либо из 5 человек:
Основные элементы комбинаторики.
Слайд 70
Задача.7.
Десять команд участвуют в разыгрывание первенства по футболу, лучшие
из которых занимают 1-е, 2-е и 3-е места. Две команды,
занявшие последние места не будут участвовать в следующем таком же первенстве. Сколько разных вариантов результата первенства может будут учитывать, если только положение первых трех и последних 2-х команд?
Решение:
1-е три места может будут распределены: способ
Остается 7 команд, две из которых выбывают из следующего первенства т.к. порядок выбывших команд не учитывается => способом.
Тогда число возможных результатов =
Основные элементы комбинаторики.
Слайд 71
Решение задач.
Задача.8.
Сколько существует вариантов опроса 11 учащихся на одном
занятии, если ни один из них не будет вызван дважды
и на занятии может будет опрошено любое количество учащихся, порядок опроса не важен?
Решение:
может не спросить ни одного, т.е. ,
если только 1, то ,
если только 2-х, то и т.д.
Тогда он всего опросит