ПРЕОБРАЗОВАНИЕ ЧЕРТЕЖА. ЗАМЕНА ПЛОСКОСТЕЙ ПРОЕКЦИЙ

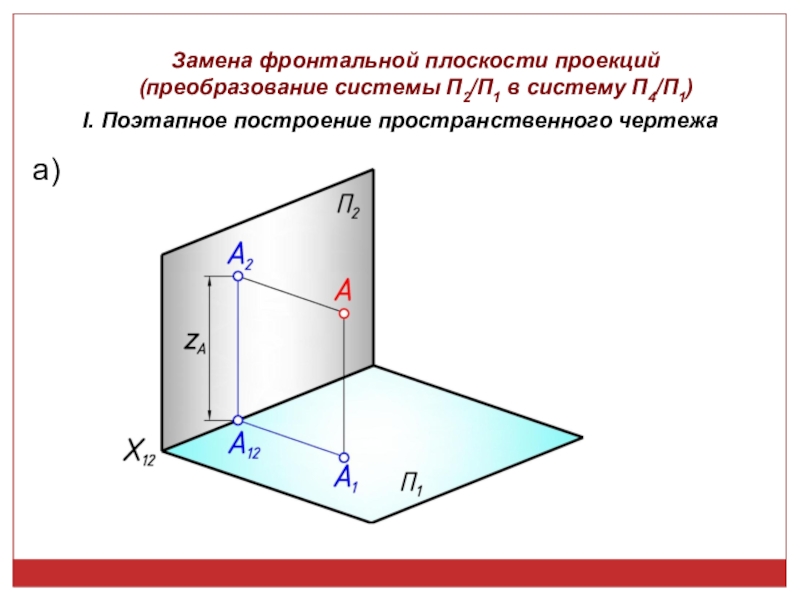
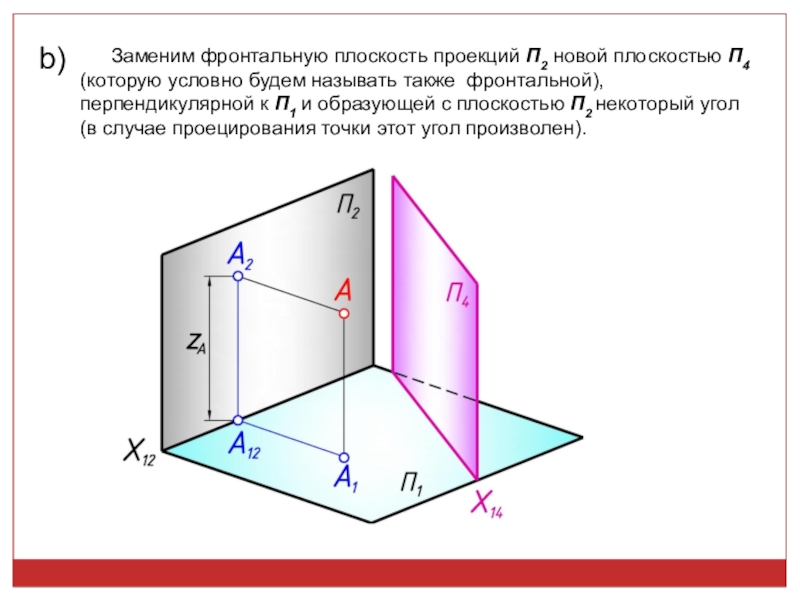
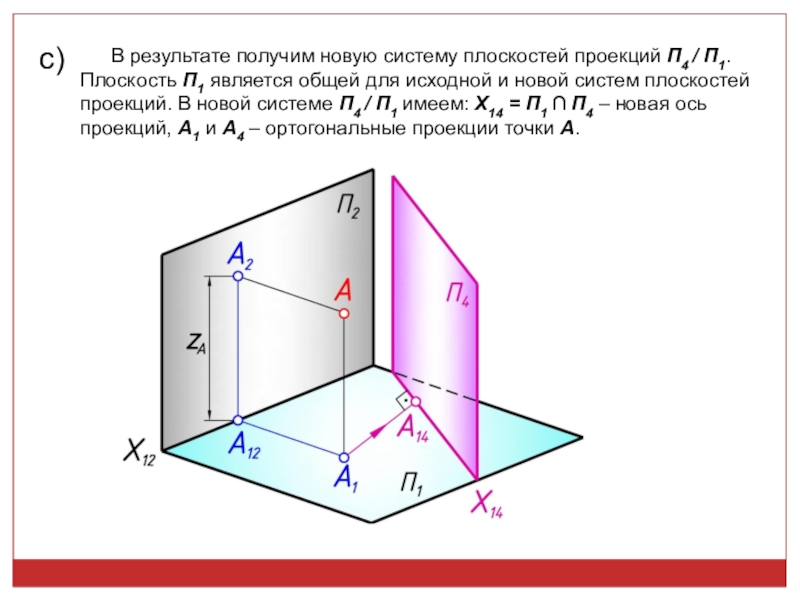
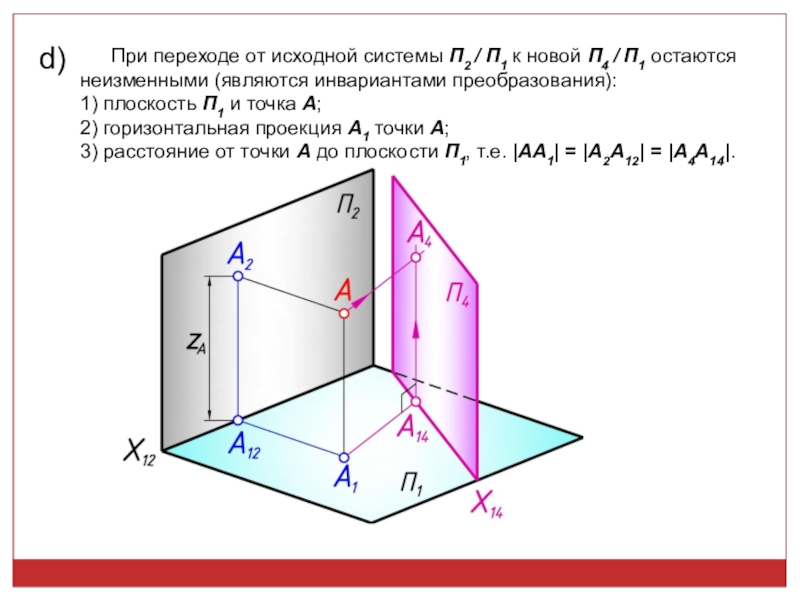
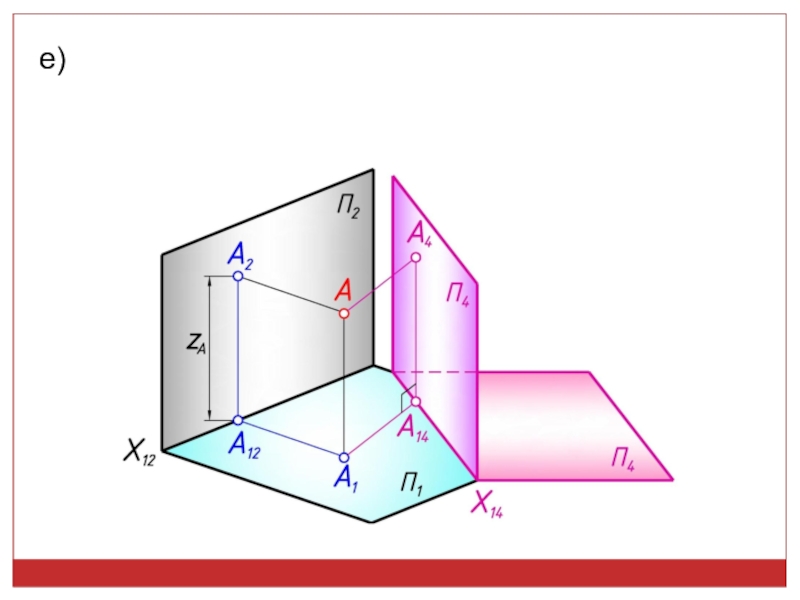
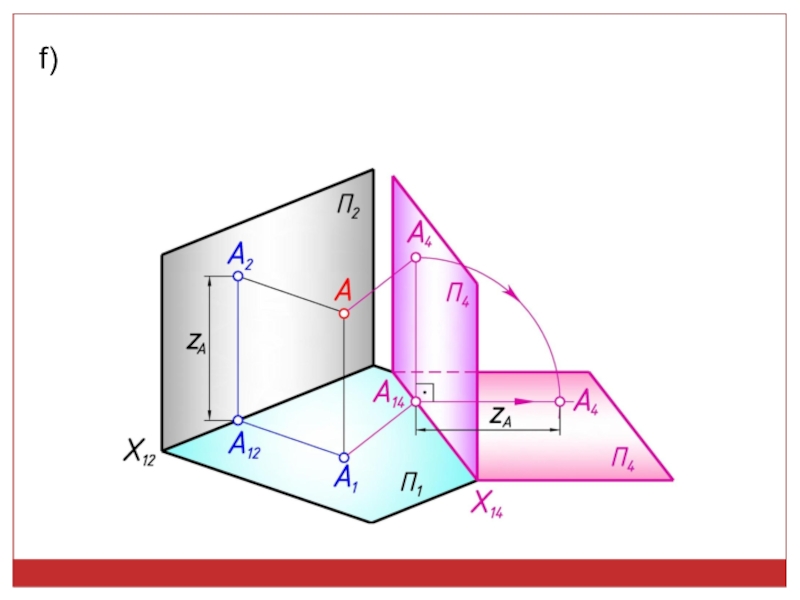
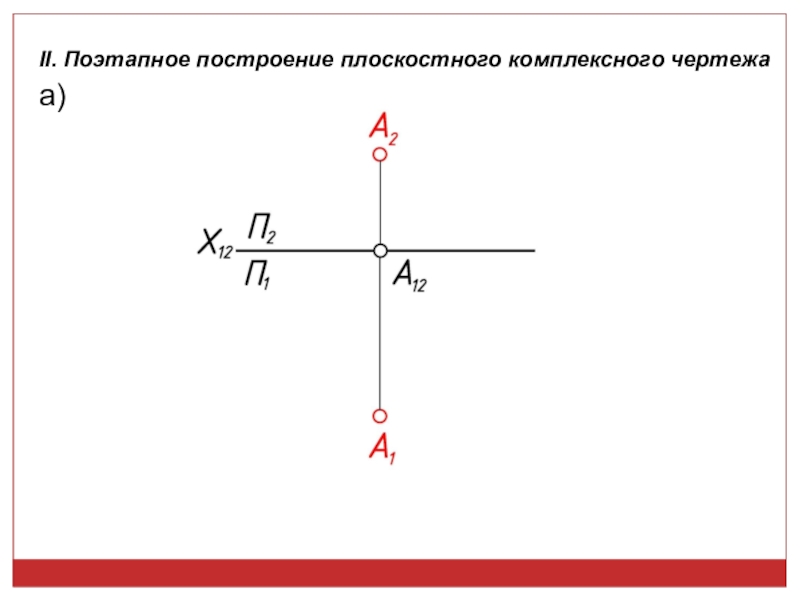
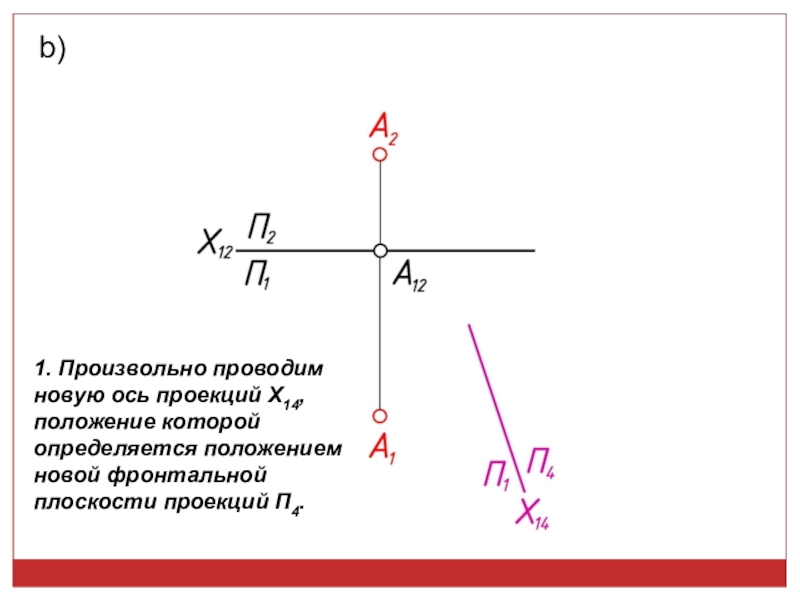
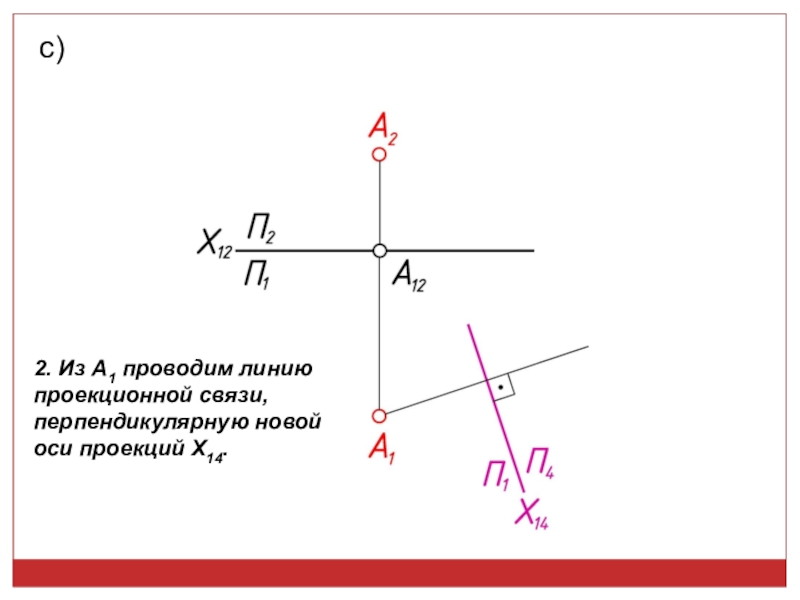
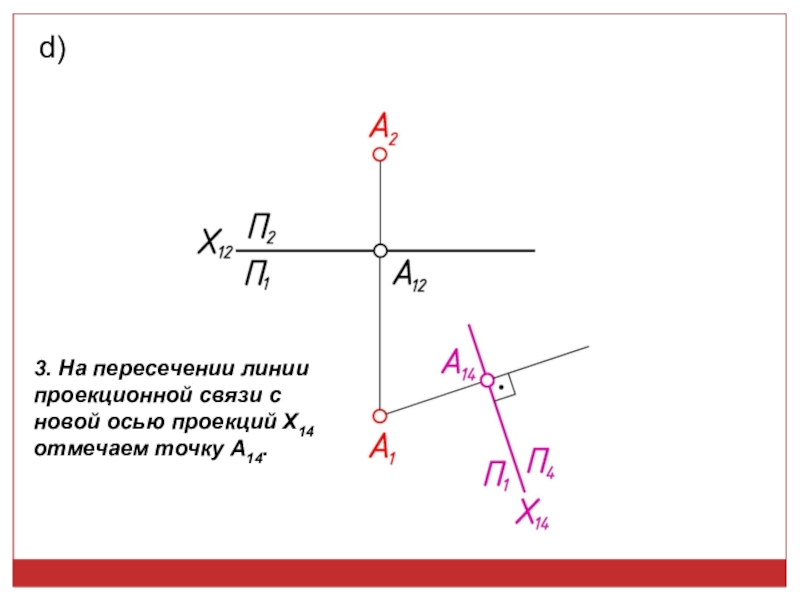
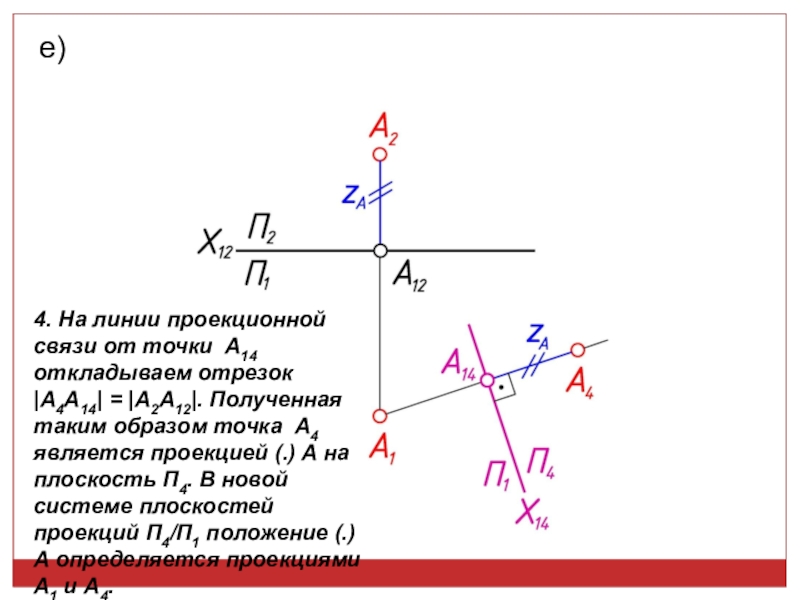
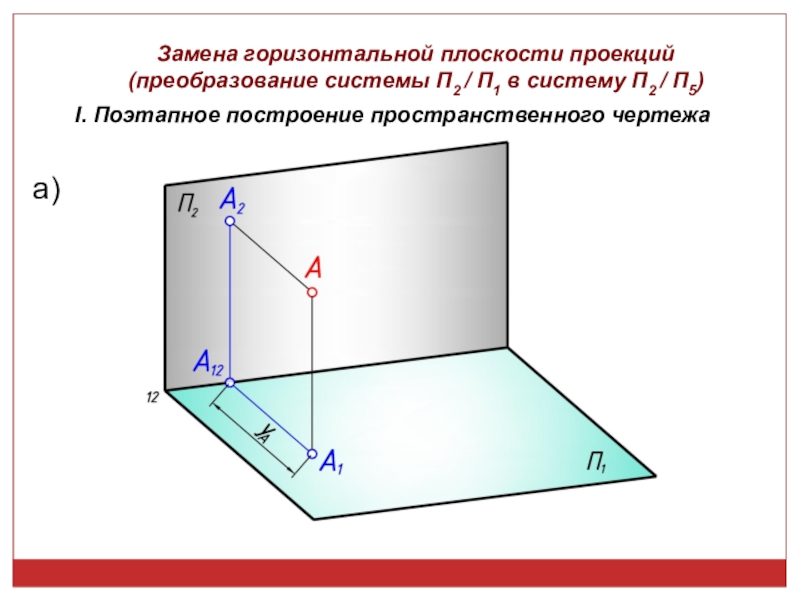
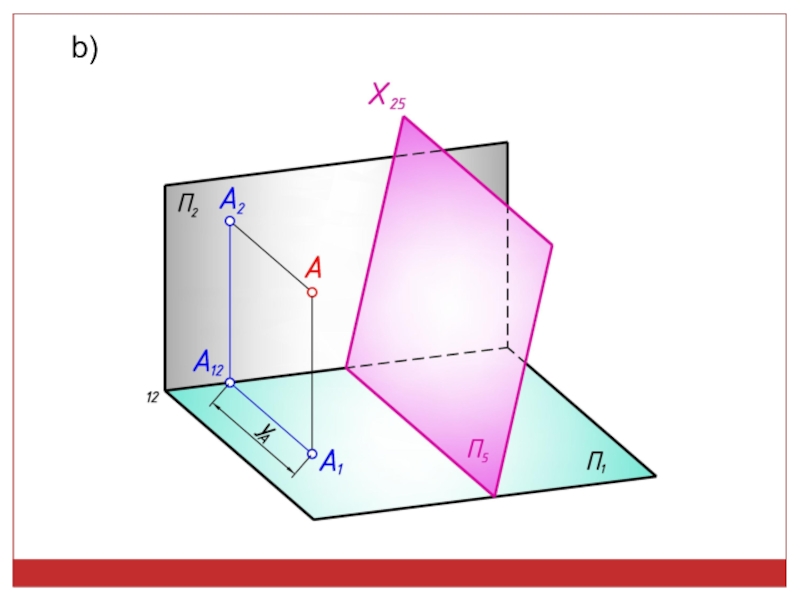
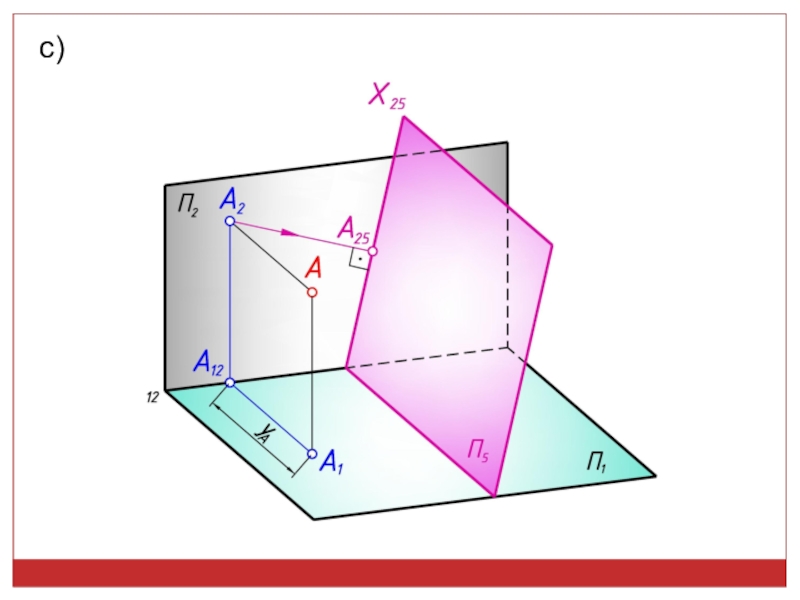
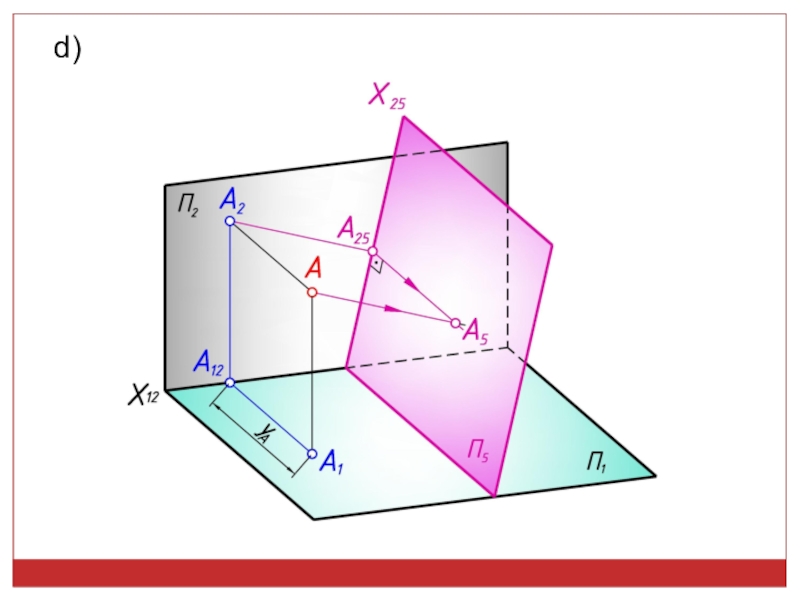
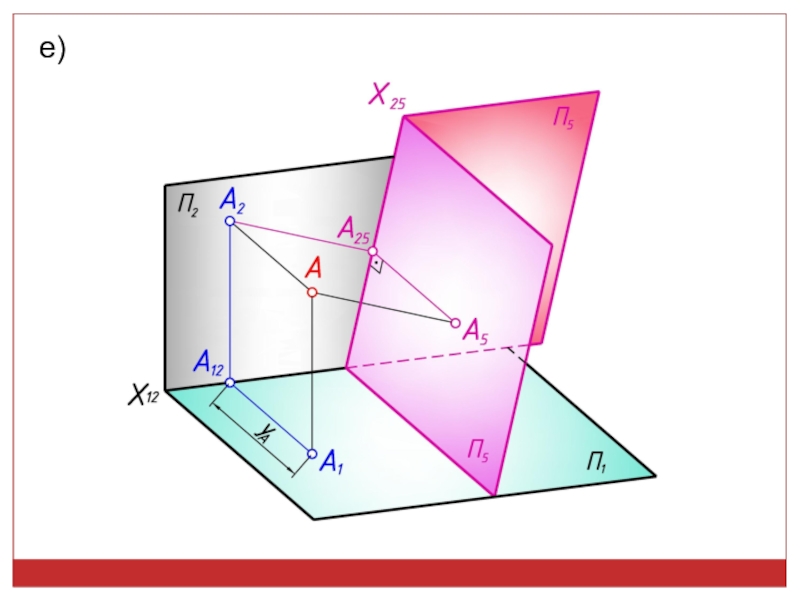
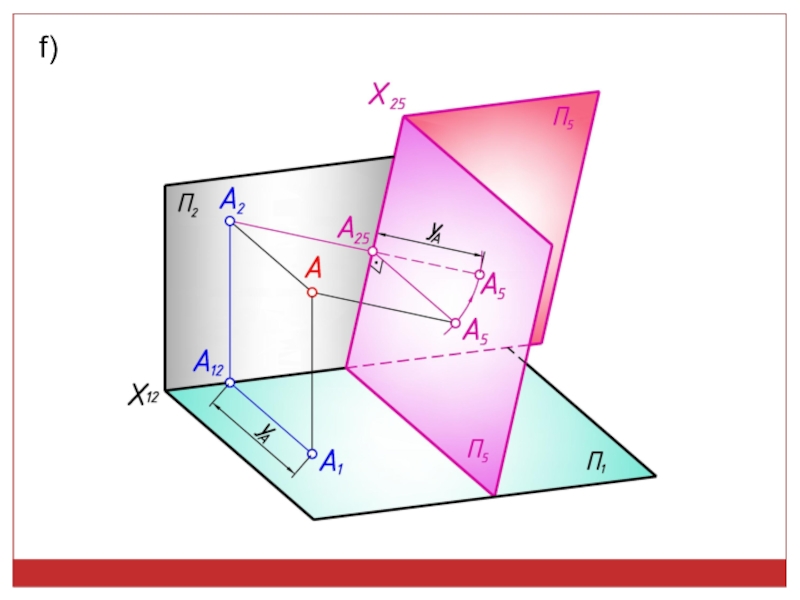
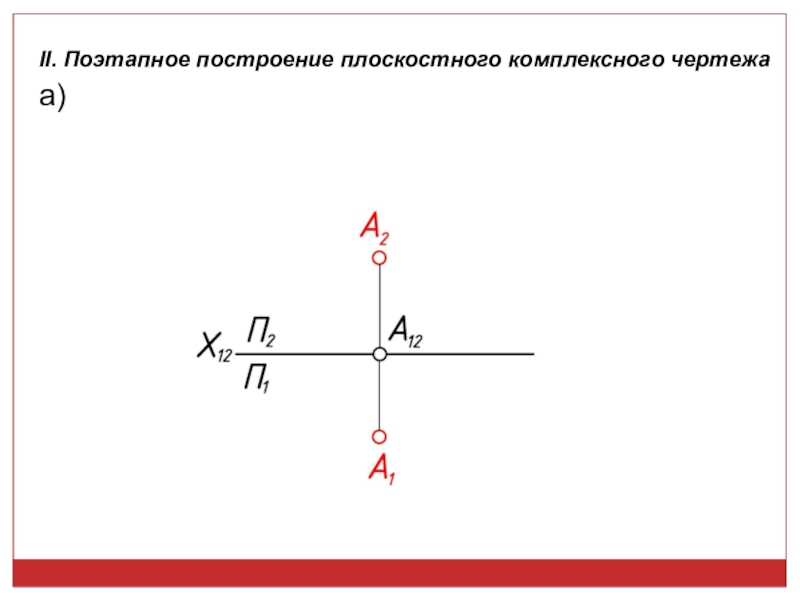
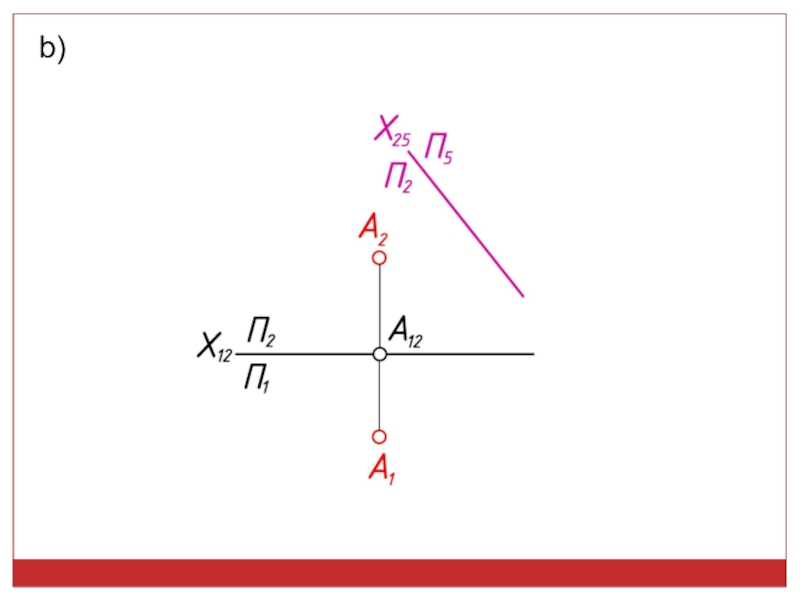
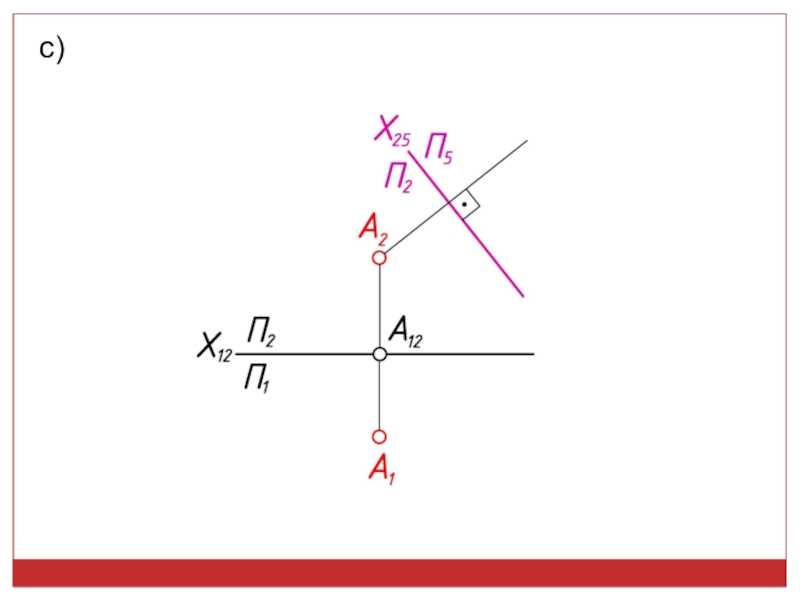
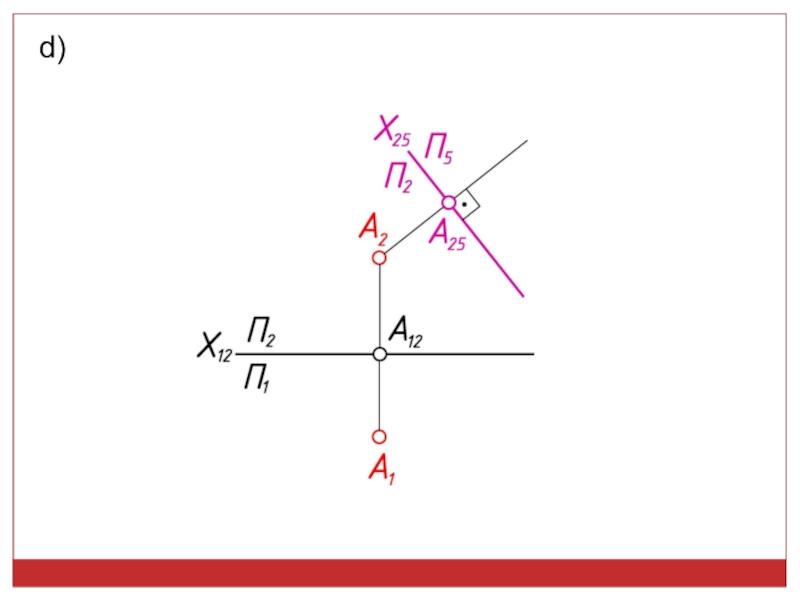
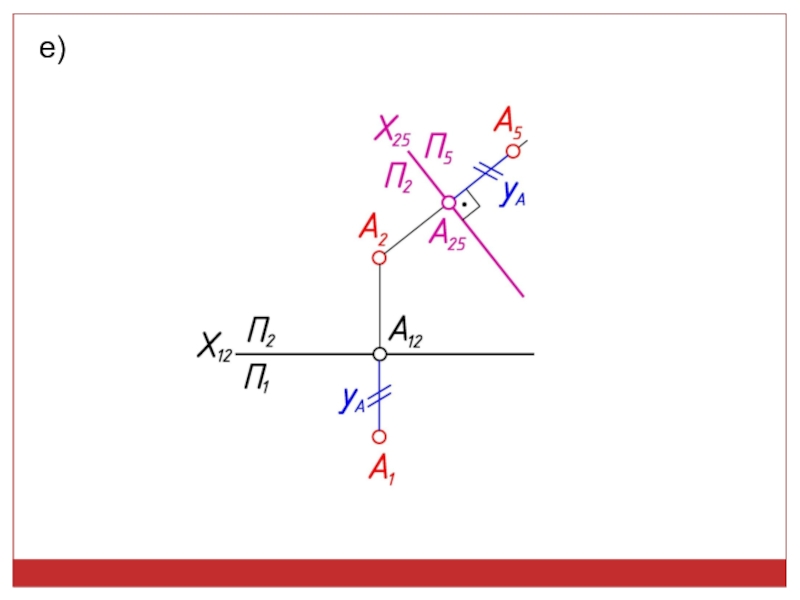
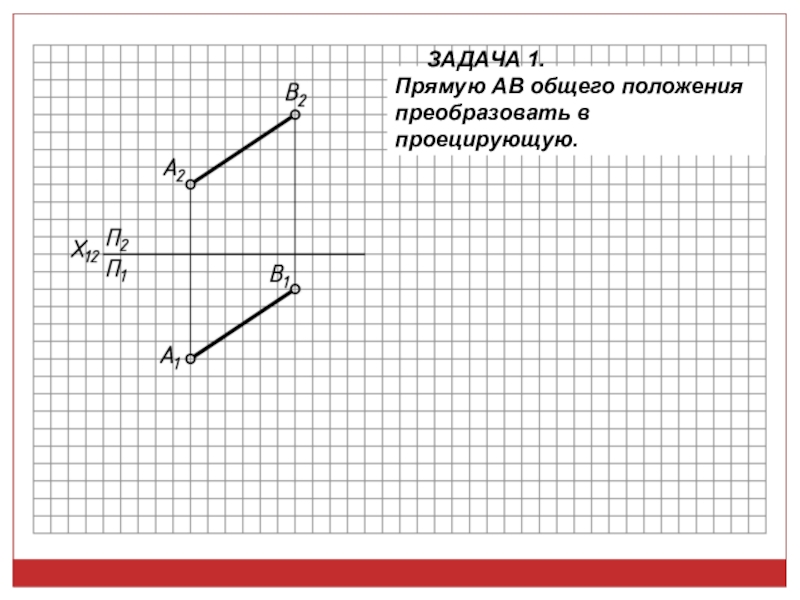
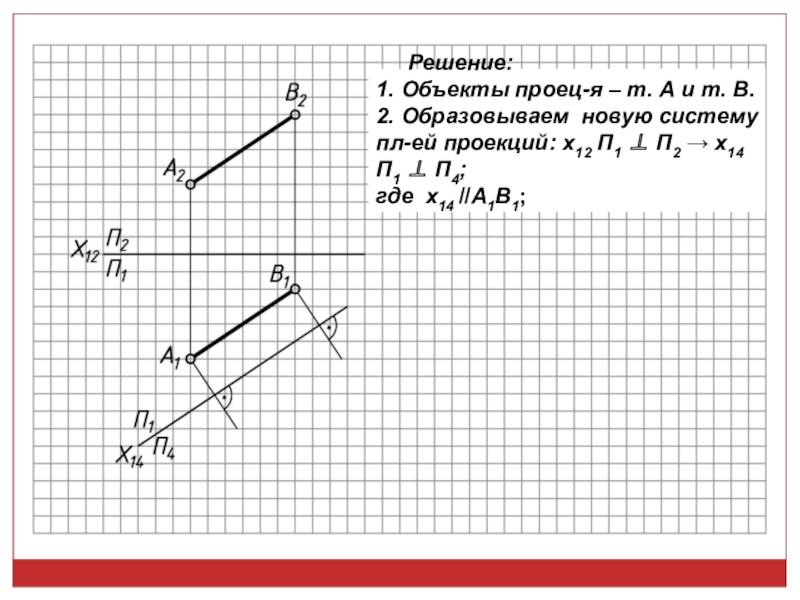
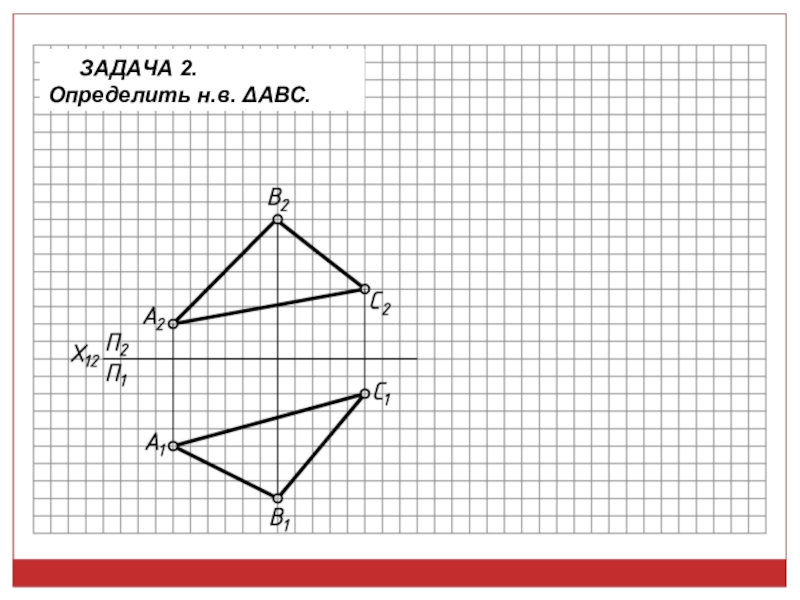
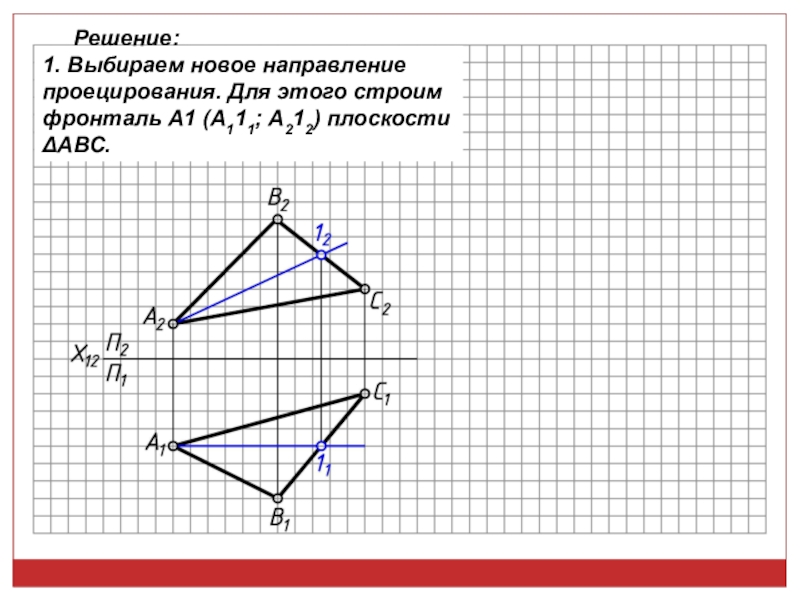
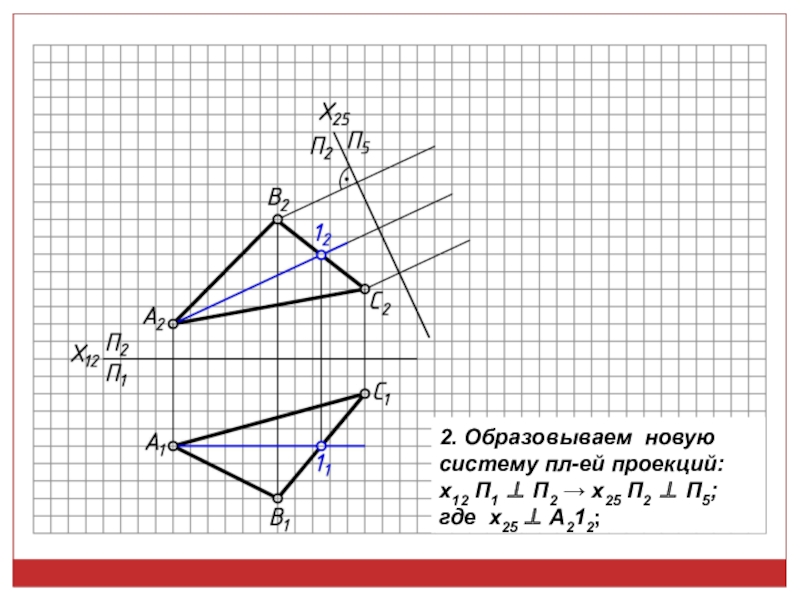
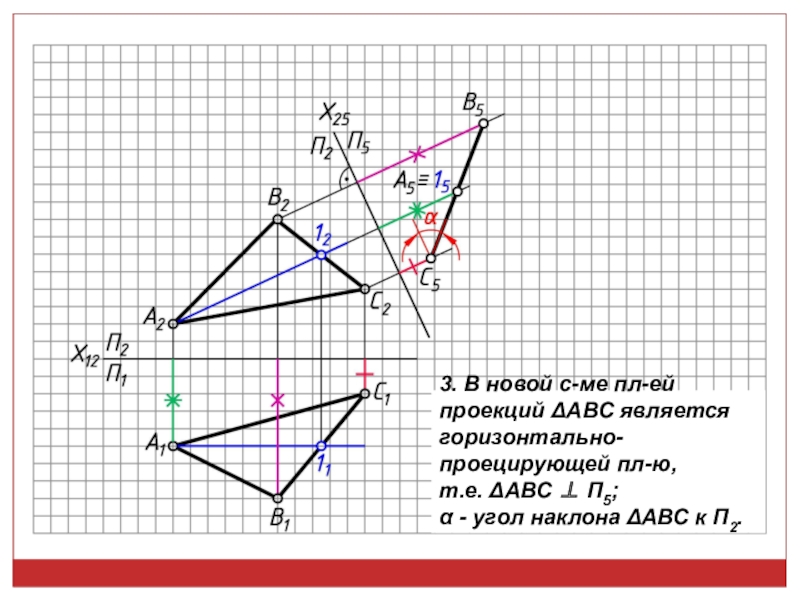
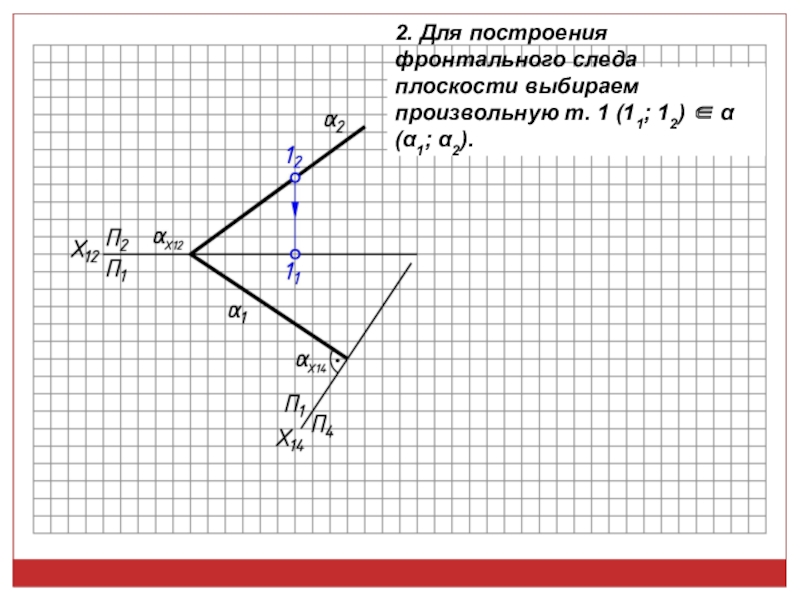
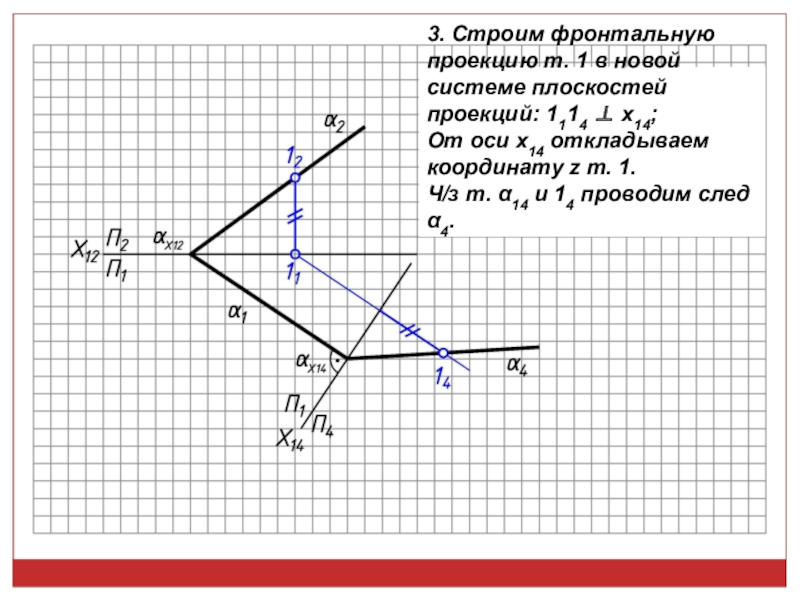
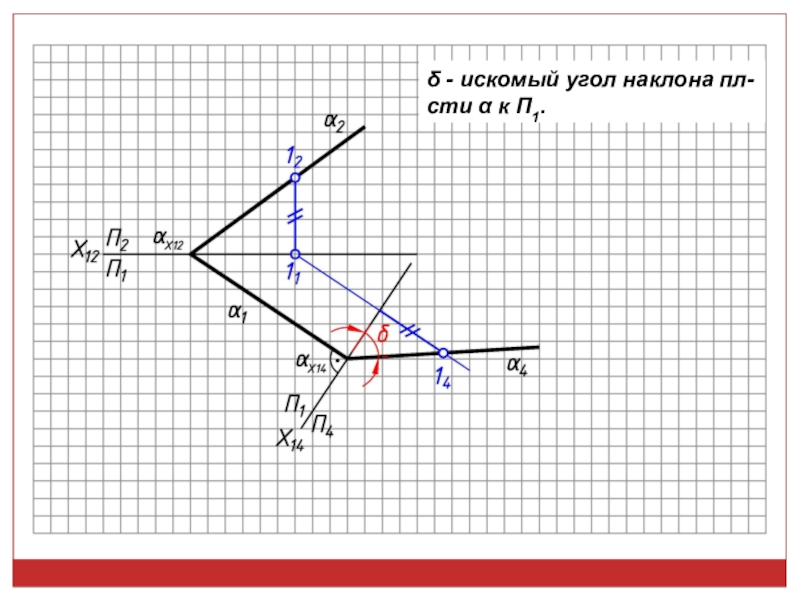
точек, линий, плоских фигур и поверхностей в пространстве остается неизменным,

а система Π1, Π2 дополняется плоскостями, образующими с Π1, или Π2, или м/д собой систему 2-х взаимно -ых пл-стей, принимаемых за пл-сти проекций.

Каждая новая система выбирается так, чтобы получить положение наиболее удобное для выполнения требуемого построения:

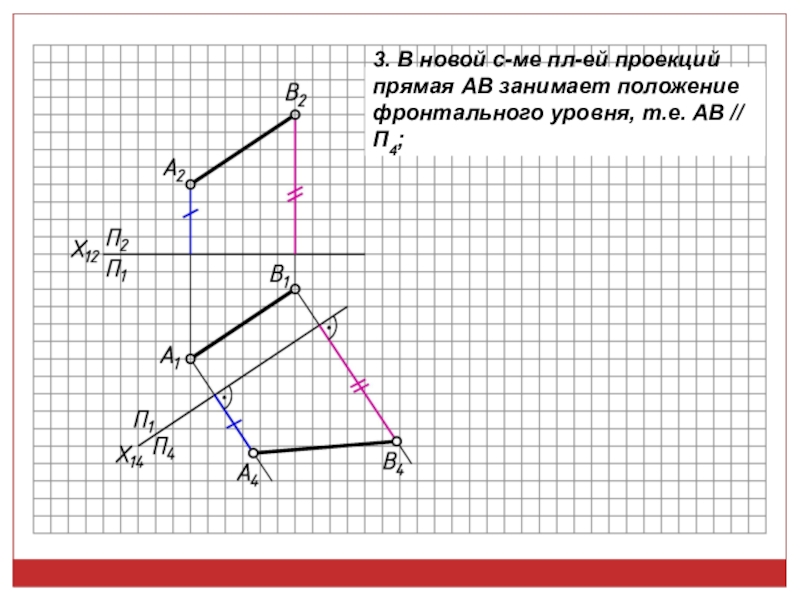
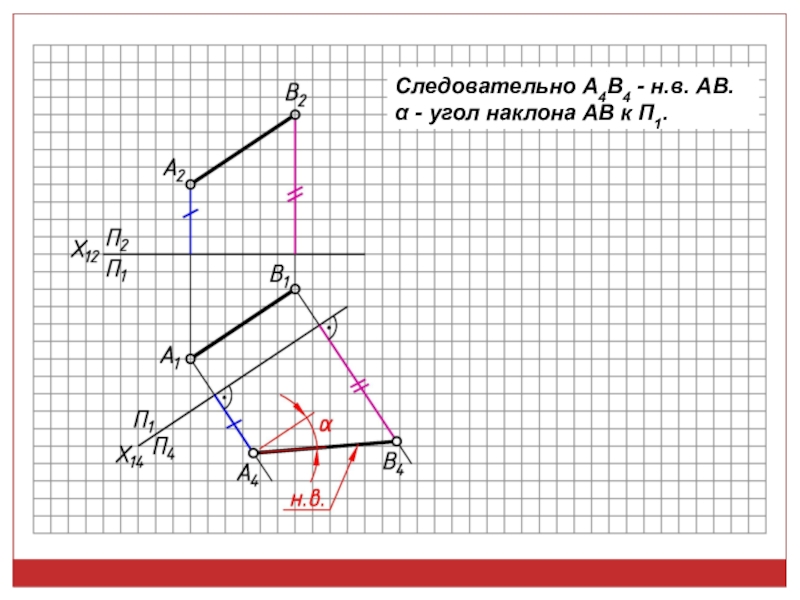
• Если отрезок или плоская фигура -ны (параллельны) плоскости проекций, то на эту плоскость они будут проец-ся (проецироватся) в н.в. (натуральную величину);
• Расстояние между скрещивающимися прямыми проец-ся в н.в., когда одна прямая проецирующая;
• Двугранный угол проец-ся в н.в, если его общее ребро занимает проецирующее положение;
• Расстояние от точки до пл-ти проец-ся в н.в., если эта пл-ть -на (перпендикулярна) пл-ти проекций;
• Угол м/д прямой и пл-тью проец-ся в н.в. в случае, когда прямая -на, а пл-ть -на одной и той же пл-сти проекций;
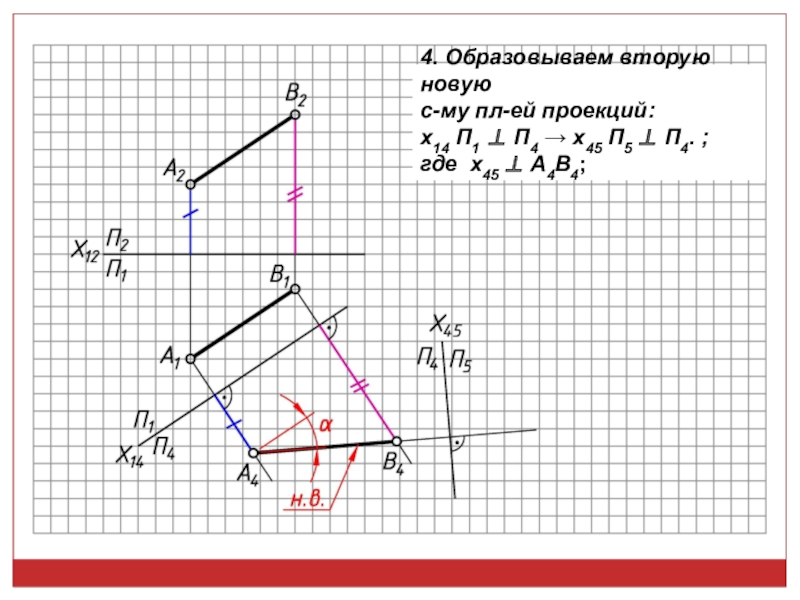
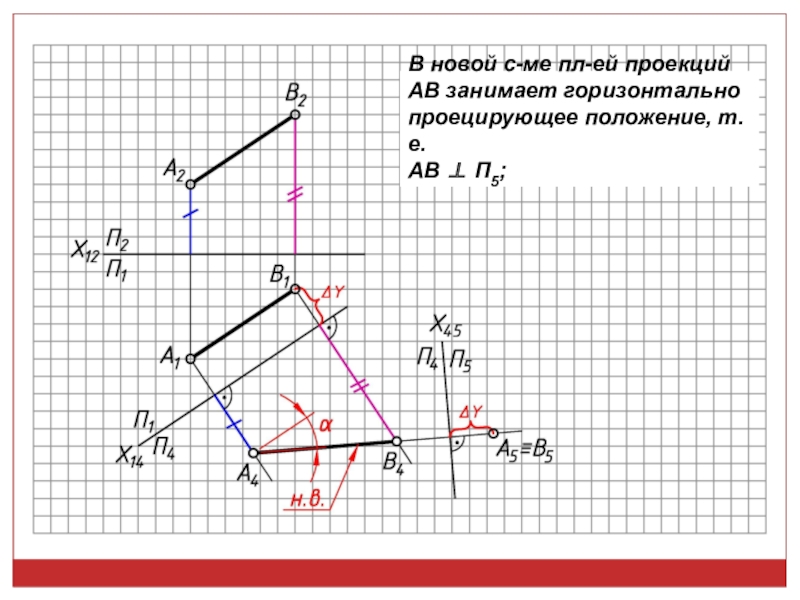
• Расстояние между двумя -ми прямыми проец-ся в н.в., если они обе являются проецирующими.

ортогональные проекции (.) А;
Π2 / Π1 – исходная система плоскостей

проекций;
Х12 = Π1 ∩ Π2 – исходная ось проекций;
Π4 / Π1 (Π2 / Π5 ) – новая система плоскостей проекций;
Х14 = Π1 ∩ Π4 (Х25 = Π2 ∩ Π5) – новая ось проекций;
А1 (А2) и А4 (А5) – ортогональные проекции точки А в новой системе плоскостей проекций.

Поэтапное построение пространственного чертежа

будем называть также фронтальной), перпендикулярной к Π1 и образующей с

плоскостью Π2 некоторый угол (в случае проецирования точки этот угол произволен).

Плоскость Π1 является общей для исходной и новой систем плоскостей

проекций. В новой системе Π4 / Π1 имеем: Х14 = Π1 ∩ Π4 – новая ось проекций, А1 и А4 – ортогональные проекции точки А.

Π4 / Π1 остаются неизменными (являются инвариантами преобразования):
1) плоскость Π1

и точка А;
2) горизонтальная проекция А1 точки А;
3) расстояние от точки А до плоскости Π1, т.е. |АА1| = |А2А12| = |А4А14|.

положением новой фронтальной плоскости проекций Π4.

проекций Х14.

Х14 отмечаем точку А14.

|А4А14| = |А2А12|. Полученная таким образом точка А4 является проекцией

(.) А на плоскость Π4. В новой системе плоскостей проекций Π4/Π1 положение (.) А определяется проекциями А1 и А4.

П2 / П5)
a)
I. Поэтапное построение пространственного чертежа

новую систему пл-ей проекций: x12 П1  П2 → x14

П1  П4; где x14 //A1В1;

фронтального уровня, т.е. АВ // П4;

П1.

→ x45 П5  П4. ; где x45  A4B4;

т.е. АВ  П5;

(А111; А212) плоскости АВС.

x25 П2  П5; где x25  A212;

АВС  П5;
 - угол наклона АВС к П2.

x45 П4  П5; где x45 // C5B5;

уровня, т.е. АВС // П4; следовательно А4В4С4 – н.в. АВС.

x14 П1  П4; где x14  1;

(11; 12)   (1; 2).

проекций: 1114  х14;
От оси х14 откладываем координату z

т. 1.
Ч/з т. α14 и 14 проводим след 4.