Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Приближенные числа Введение Представление чисел в ЭВМ Понятие
Содержание
- 1. Приближенные числа Введение Представление чисел в ЭВМ Понятие
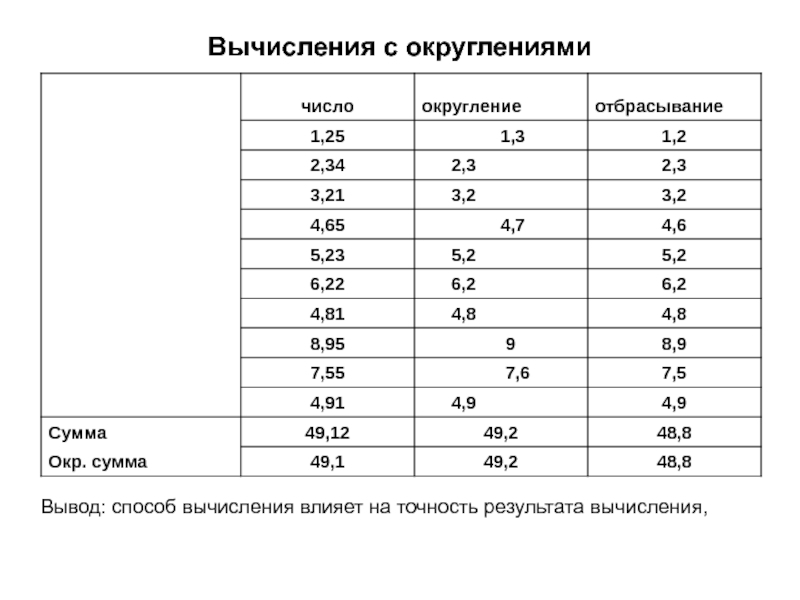
- 2. Вычисления с округлениямиВывод: способ вычисления влияет на точность результата вычисления,
- 3. Приближенные числа в компьютерных вычисленияхПредставление чисел в
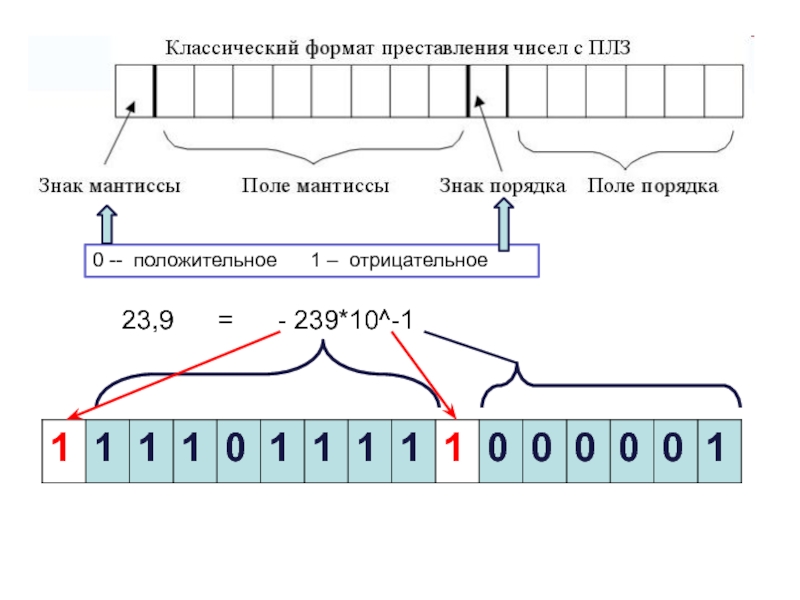
- 4. 23,9 = - 239*10^-10 -- положительное 1 – отрицательное
- 5. ПогрешностьПогрешность есть мера точности приближенных чисел.Абсолютная погрешность
- 6. Действия над приближенными числами Абсолютная погрешность арифметических действий
- 7. Относительная погрешность арифметических действийОтносительная погрешность суммы положительных
- 8. Слайд 8
- 9. Рассмотрим пример:Пусть а = 2520, в =
- 10. Погрешности функцийПогрешность аргумента ∆а рассматриваем как изменениеаргумента,
- 11. Источники погрешностейМатематическая модель, принятая для описания данного
- 12. Устойчивость. Корректность. СходимостьЧувствительность метода к неточностям в
- 13. Двоичное исчисление2^0=12^1=22^2=42^3=82^4=162^5=322^6=642^7=1282^8=2562^8=5122^9=1024Дв Дс
- 14. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Приближенные
числа
Введение
Представление чисел в ЭВМ
Понятие погрешности
Погрешности функций
Устойчивость, корректность, съодимость
Приложение –
системы исчисления
Слайд 3Приближенные числа в компьютерных вычислениях
Представление чисел в ЭВМ используется 4
байта памяти (32 разряда)
00000000 00000000 00000000 00000000
Пример распределения 16 разрядов:=>
-2 • 10^15 до 2 • 10^15 Для расширения числового диапазона используется
запись с плавающей запятой
D = ±m • 10", где т и п — соответственно мантисса числа и его порядок.
Например, число -23.9 можно записать в виде:
-2,39 • 10^1, —0.239 • 10^2, - 239*10^-1
2^9=1024
1,0000
1,0001
………
1,1024
2,0000
Слайд 5Погрешность
Погрешность есть мера точности приближенных чисел.
Абсолютная погрешность некоторого числа равна
разности между его
истинным значением и приближенным значением, полученным в
результате вычисления или измерения.
Относительная погрешность — это отношение абсолютной
погрешности к приближенному значению числа.
Для приближенного числа, полученного в результате округления,
абсолютная погрешность принимается равной половине единицы
разряда, следующего за значащим
0,734 =>0,73431, =>0,73357 – погрешность округления = 0,0005
Если при вычислениях на компьютере округление не производится,
а цифры, выходящие за разрядную сетку машины, отбрасываются,
то максимально возможная погрешность результата выполнения операции
в два раза больше по сравнению со случаем округления.
Слайд 7Относительная погрешность арифметических действий
Относительная погрешность суммы положительных слагаемых заключена
между
наибольшим и наименьшим значениями относительных погрешностей
этих слагаемых. М –
максимальное значение (σа и σв), принимают для расчетовСлайд 9Рассмотрим пример:
Пусть а = 2520, в = 2518. Найти относительную
погрешность разности
двух чисел.
Вывод: относительная погрешность результата равна 50%,
т.е. ожидаемый результат
равен 2 +- 1,или 1
Слайд 10Погрешности функций
Погрешность аргумента ∆а рассматриваем как изменение
аргумента, при этом изменение
функции можно определить
используя дифференцирование
Для сложной функции находим аналогично
Где, ∆а, ∆в,
∆с – соответственно погрешности аргументовСлайд 11Источники погрешностей
Математическая модель, принятая для описания данного процесса или
явления,
может внести существенные погрешности, если в ней не
учтены какие-либо
важные черты рассматриваемой задачи. 2. Исходные данные задачи часто являются основным источником
погрешностей. Вместе с погрешностями, вносимыми математической
моделью, их называют неустранимыми погрешностями, поскольку они
не могут быть уменьшены вычислителем ни до начала решения задачи,
ни в процессе ее решения.
3. Численный метод также является источником погрешностей. Это связано,
например, с заменой интеграла суммой, с усечением рядов при вычислениях
значений функций, с интерполированием табличных данных и т. п. Как правило,
погрешность численного метода регулируема, т. е. теоретически она может
быть уменьшена до любого значения путем изменения некоторого параметра
(например, шага интегрирования, числа членов усеченного ряда и т. п.).
4. При вычислениях с помощью компьютера неизбежны погрешности
округлений,(отбрасываний) связанные с ограниченностью разрядной сетки ЭВМ
Слайд 12Устойчивость. Корректность. Сходимость
Чувствительность метода к неточностям в исходных данных.
характеризуется
так называемой устойчивостью, или малые погрешности
в исходных данных приводят
к малым погрешностям в решении.Задача называется поставленной корректно, если для любых
значений исходных данных из некоторого класса ее решение
существует, единственно и устойчиво по исходным данным.
При анализе точности вычислительного процесса одним из важнейших
критериев является сходимость численного метода. Она означает
близость получаемого численного решения задачи к истинному решению.
(итерационные методы, методы дискретизации, интегрирование..)
Конец лекции
Слайд 13Двоичное исчисление
2^0=1
2^1=2
2^2=4
2^3=8
2^4=16
2^5=32
2^6=64
2^7=128
2^8=256
2^8=512
2^9=1024
Дв Дс Шест Вс
3210_______________
0000 =
0
0001 = 1
0010 = 2
0011 = 3
0100 = 4
0101 =
50110 = 6
0111 = 7
1000 = 8 10
1001 = 9 11
1010 = 10 A 12
1011 = 11 B 13
1100 = 12 C 14
1101 = 13 D 15
1110 = 14 E 16
1111 = 15 F 17
i- номер позиции (слева)двоичного кода
K – значение позиции, 1или 0
1010 = 1*2^3+0*2^2+1*2^1+0*2^0 =8+0+2+0=10
Шестнадцатеричная система
C5 = 12*16+5 = 197:
8F = 8*16+15 = 143
Восьмеричная система
26=2*8+6=22
121 = 1*64 +2*8+1=81