Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Причинный анализ и регрессии
Содержание
- 1. Причинный анализ и регрессии
- 2. Причинный анализИмеет место какое-либо социальное явление, которое
- 3. Отношения между структурными переменнымиXY (х обусловливает у)XY (у обусловливает х)XY (взаимное воздействие)X – Y (нет связи)
- 4. Регрессионный анализметод выявления статистической зависимости между исследуемыми
- 5. Регрессия может быть:Парной (однофакторной) и множественной (многофакторной).
- 6. При построении моделей регрессии должны соблюдаться следующие
- 7. Линейный регрессионный анализТехника регрессионного анализа, позволяющая выявлять
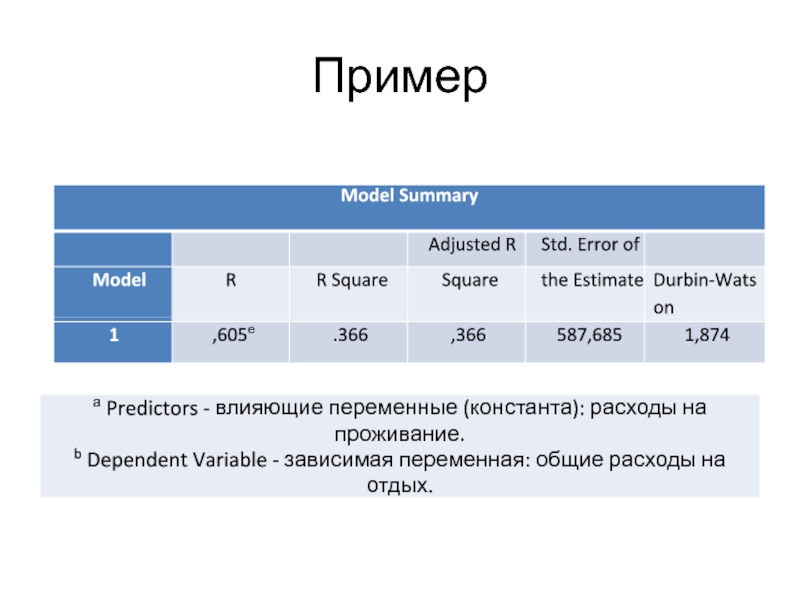
- 8. Оценка качества линейной регрессии: коэффициент множественной корреляцииКоэффициент
- 9. Коэффициент множественной детерминации (R-square)доля общей дисперсии, которая
- 10. Требования к переменным:Переменные должны быть измерены в
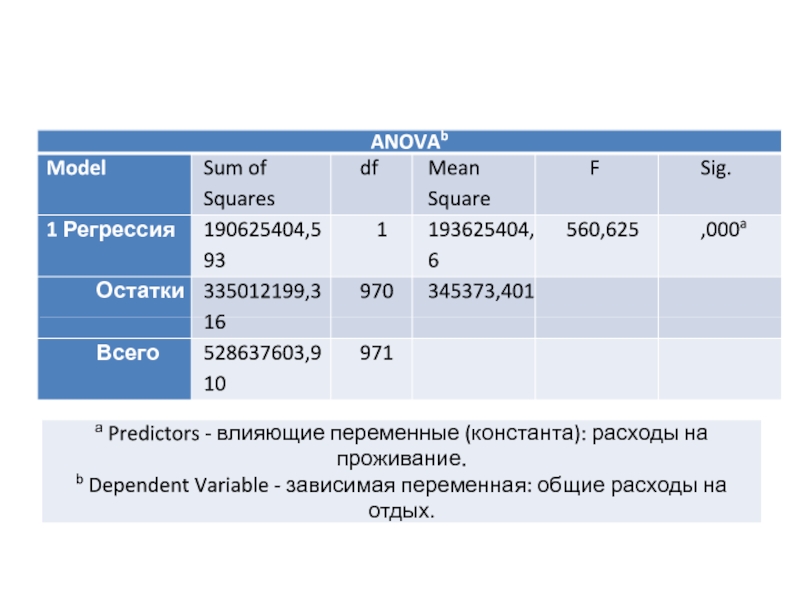
- 11. Пример
- 12. Слайд 12
- 13. Слайд 13
- 14. Слайд 14
- 15. Скачать презентанцию
Причинный анализИмеет место какое-либо социальное явление, которое характеризуется переменной Х. Оно зависит и причинно обусловлено другими данными социальными явлениями, характеризуемыми другими переменными соответственно У, Z.
Слайды и текст этой презентации
Слайд 2Причинный анализ
Имеет место какое-либо социальное явление, которое характеризуется переменной Х.
другими переменными соответственно У, Z.
Слайд 3Отношения между структурными переменными
XY (х обусловливает у)
XY (у обусловливает х)
XY
(взаимное воздействие)
X – Y (нет связи)
Слайд 4Регрессионный анализ
метод выявления статистической зависимости между исследуемыми переменными.
заключается в
определении аналитического выражения связи, в котором изменение одной величины обусловлено
влиянием одной или нескольких независимых величин.Слайд 5Регрессия может быть:
Парной (однофакторной) и множественной (многофакторной).
По форме зависимости
– линейной и нелинейной;
По направлению связи:
прямая (положительная), возникающая при условии,
если с увеличением или уменьшением независимой величины значения зависимой также соответственно увеличиваются или уменьшаются;обратная (отрицательная), проявляющаяся при условии, что с увеличением или уменьшением независимой величины зависимая соответственно уменьшается или увеличивается.
Слайд 6При построении моделей регрессии должны соблюдаться следующие требования:
1. Совокупность исследуемых
исходных данных должна быть однородной и описываться непрерывными функциями.
2. Моделируемые
явления должны оцениваться одним или несколькими уравнениями причинно-следственных связей.3. Все признаки должны иметь количественное (цифровое) выражение.
4. Наличие достаточно большого объема исследуемой выборочной совокупности. Обычно считают, что число наблюдений должно быть не менее чем в 5-6, а лучше – не менее чем в 10 раз больше числа факторов.
5. Отсутствие количественных ограничений на параметры модели связи.
Слайд 7Линейный регрессионный анализ
Техника регрессионного анализа, позволяющая выявлять и описывать взаимосвязи
в виде линейных функций, называется линейным регрессионным анализом.
Слайд 8Оценка качества линейной регрессии: коэффициент множественной корреляции
Коэффициент R является характеристикой
общей силы линейной связи между переменными.
Значения коэффициента находятся в
интервале от 0 до 1. Чем ближе значение коэффициента к 1, тем плотнее линейная взаимосвязь, описанная в регрессионной модели.
Должен превышать 0,5.
Слайд 9Коэффициент множественной детерминации (R-square)
доля общей дисперсии, которая объясняется регрессией и
выражается через процентное соотношение.
Позволяет субъективно оценить качество уравнения регрессии.
Разность (100-R^2) - процент
дисперсии, который нельзя объяснить регрессией. Слайд 10Требования к переменным:
Переменные должны быть измерены в шкале интервалов или
отношений (количественные/метрические)
Нормальное распределение переменных
Отсутствие линейных взаимосвязей между переменными, когда одна
переменная является линейной производной другой переменной (корреляция больше 0,8 – bad)Число варьирующих признаков в сравниваемых переменных должно быть одинаковым