Слайд 1ПРИКЛАДНЫЕ МЕТОДЫ ОПТИМИЗАЦИИ
Слайд 2Выполнил :Корнилов М.А.
Группа 171-724
Слайд 3ПРЕДИСЛОВИЕ
Современное общество характеризуется стремительным развитием технического прогресса, усложнением экономических
отношений и организационной структуры производства, предъявлением высоких требований к методам
планирования и управления. Одним из необходимых условий такого развития является широкое использование информационных и телекоммуникационных технологий и методов анализа и принятия оптимальных решений.
Предлагаемая вниманию книга предназначена для изучения принципов и методов оптимизации различных процессов, для которых возможна их математическая или графическая формализация.
Данная книга сформировалась в результате обобщения научного опыта автора, полученного при выполнении фундаментальных (грантовых) и прикладных (хоздоговорных) проектов и чтении лекций студентам, магистрантам и докторантам Казахского национального исследовательского технического университета им. К.И. Сатпаева (КазНИТУ). Автор попытался осуществить плавный переход от классических методов оптимиза- ции к методам математического программирования и изложить материал с единой точки зрения в достаточно строгой, но доступной форме.
Книга состоит из введения и восьми разделов, которые условно можно разбить на две части.
Во введении приведены основные понятия и классификация методов оптимизаций.
В первой части (разделы с 1 по 7) рассмотрены классический аппарат оптимизации, основные направления (линейное, целочисленное, нелинейное программирование и транспортные задачи) математического программирования, динамическое программирование и методы решения сетевых задач.
Во второй части (раздел 8) приведены отдельные, переработанные для учебной цели, результаты грантовых и хоздоговорных исследований, выполненных в разные годы под научным руководством автора. Эти результаты являются, по мнению автора, наглядной иллюстрацией того, что необходимость принятия оптимальных решений злободневна во всех областях и сферах деятельности человека.
Книга рассчитана на специалистов, студентов, магистрантов и докторантов, интересующихся методами оптимизации в научных и приклад- ных исследованиях.
Предлагаемая читателю книга не могла быть написано без активной поддержки коллег по кафедре информационных технологий КазНИТУ. Большую помощь при подготовке рукописи книги оказали докторант Жанар Бимурат и студент Рамазан Мусаров. Всем им автор весьма признателен.

Слайд 4В.1. Основные понятия и положения методов оптимизации
Предметом методов оптимизации
является задача определения наилучших по заданному критерию решений при наличии
или отсутствии некоторых ограничивающих условий, т.е. оптимизационная задача. Модель оптимизационной задачи, в общем случае, состоит из целевой функции, являющейся кратким математическим описанием цели (критерия) задачи и уравнений и (или) неравенств, описывающих ограничения.
Введем следующие основные понятия методов оптимизации: – конечномерная задача оптимизации – эта задача, для которой выполняется условие X ⊆ En, где Х – допустимое множество решений оптимизационной задачи, а En – n-мерное евклидово пространство;
– множество Х называется компактом, если оно замкнутое ограниченное множество;
– множество Х является выпуклым, если любая его точка, лежащая между двумя допустимыми точками также допустимая;
– допустимое значение переменной оптимизационной задачи удовлетворяет условию х ∈ Х;
– целевая функция f(x), определенная на выпуклом множестве Х является выпуклой на Х, если
f(λx1 + (1 – λ)x2) ≤ λf(x1) + (1 – λ)f(x2) при всех x1, x2 ∈ X, λ ∈ [0, 1]. Функция f(x) называется вогнутой, если {–f(x)} выпукла;
Наиболее общая постановка задачи оптимизации имеет следующий вид f(x) → extremum, x ∈ X. (В.1) Для конкретности предположим, что extremum это maximum
f(x) → maximum, x ∈ X. (В.2) Решение x* ∈ X называется: – глобальным максимумом целевой функции f(x) на множестве Х, если f(x*) ≥ f(x) для ∀x ∈ X; (В.3) – локальным максимумом целевой функции f(x) на множестве Х, если f(x*) ≥ f(x) для «(x ± ε) ∈ X. (В.4)
Глобальный максимумом является локальным, но не наоборот.

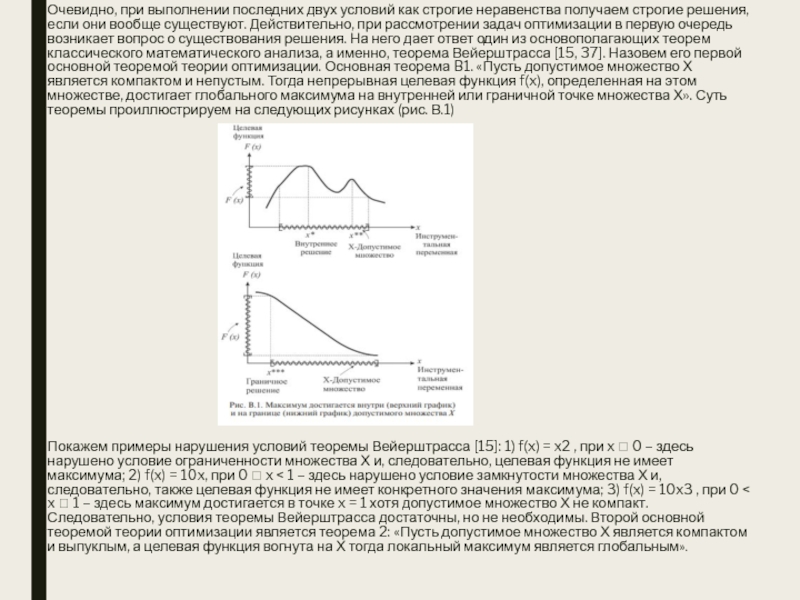
Слайд 5Очевидно, при выполнении последних двух условий как строгие неравенства получаем
строгие решения, если они вообще существуют. Действительно, при рассмотрении задач
оптимизации в первую очередь возникает вопрос о существования решения. На него дает ответ один из основополагающих теорем классического математического анализа, а именно, теорема Вейерштрасса [15, 37]. Назовем его первой основной теоремой теории оптимизации. Основная теорема B1. «Пусть допустимое множество Х является компактом и непустым. Тогда непрерывная целевая функция f(x), определенная на этом множестве, достигает глобального максимума на внутренней или граничной точке множества Х». Суть теоремы проиллюстрируем на следующих рисунках (рис. В.1)
Покажем примеры нарушения условий теоремы Вейерштрасса [15]: 1) f(x) = x2 , при x 0 – здесь нарушено условие ограниченности множества Х и, следовательно, целевая функция не имеет максимума; 2) f(x) = 10x, при 0 x < 1 – здесь нарушено условие замкнутости множества Х и, следовательно, также целевая функция не имеет конкретного значения максимума; 3) f(x) = 10x3 , при 0 < x 1 – здесь максимум достигается в точке x = 1 хотя допустимое множество Х не компакт. Следовательно, условия теоремы Вейерштрасса достаточны, но не необходимы. Второй основной теоремой теории оптимизации является теорема 2: «Пусть допустимое множество Х является компактом и выпуклым, а целевая функция вогнута на Х тогда локальный максимум является глобальным».
Слайд 6Геометрическая интерпретация теоремы 2 показана на рис. В.2 [15]. Линия
(поверхность) уровня целевой функции это множество точек для которых f(x)
= const, т.е. {x En /f(x) = const}.
Меняя const получим, как показано на рисунке, разные линии уровня. Направление, вдоль которого скорость увеличения целевой функции максимальна, называется «направлением наискорейшего подъема». Оно задается вектором, который составлен из первых частных производных целевой функции
Полученный вектор-градиент определяет, как показано на рисунке стрелкой, направление наискорейшего возрастания целевой функции.
Слайд 7В.2. Классификация методов оптимизации
В.2.1. Задачи безусловной оптимизации
Исторически первой является
задача безусловной оптимизации. Ее математическая формулировка вытекает из постановки общей
задачи оптимизации (В.1) при исключении множества Х, т.е.
Методы решения задачи безусловной оптимизации основаны на аппарате теории математического анализа для непрерывных дифференцируемых функций f(x) с небольшим числом переменных и классическом аппарате минимизации (максимизации), например градиентного метода и метода Ньютона. Существуют также методы не использующие производные, например, максимизация прямым поиском Хука-Дживса [45].
В.2.2. Классическая задача на условный экстремум
Следующим по хронологии является классическая задача на условный экстремум. Это задача (В.1) с допустимым множеством Х, заданным системой конечного числа уравнений
Общепринятой формой ее записи является
Для решения этой задачи также применяется аппарат теории математического анализа для дополнительно построенной функции Лагранжа [15].
Слайд 8В.2.3. Задача математического программирования
Задача (В.1) называется задачей математического программирования, если
ее допустимое множество имеет вид
В общепринятой форме задачу математического программирования
можно представить в виде
Термин «математическое программирование» предложен Робертом Дорфманом в 1950 году [45] и теперь он объединяет линейное программирование, целочисленное программирование, квадратичное программирование, выпуклое программирование и нелинейное программирование. Математическое программирование имеет дело с оптимизацией линейной или нелинейной целевой функции при линейных и (или) нелинейных ограничениях.
Слайд 9В.2.3.1. Линейное программирование
Наиболее разработанной и, следовательно, имеющей огромную прикладную значимость,
является задача линейного программирования. Целевая функция и ограничения задачи линейного
программирования являются линейными. Тогда множество допустимых решений может быть представлено в виде:
Саму задачу в общем случае можно записать в виде:
Основой для решения задач линейного программирования является симплекс-метод, разработанный в середине прошлого века американским математиком Дж. Данцигом. Как и все задачи математического программирования объем вычислений задачи линейного программирования быстро растет с увеличением числа переменных. Для задач линейного программирования с двух индексными переменными, получившими название «транспортные задачи», с учетом специфики структуры их ограничений разработаны более эффективные методы, такие как метод потенциалов, распределительный метод и другие [37]. В задачах целочисленного программирования, как и следует ожидать, в систему ограничений включено условие целочисленности переменных. Наиболее известными здесь являются методы Гомори и ветвей и границ.

Слайд 10В.2.3.2. Квадратичное программирование
Задачей квадратичного программирования называют задачу максимизации или минимизации
квадратичной функции при линейных ограничениях. Следовательно, множество ее допустимых решений
в общем случае совпадает с (В.9). Математическую постановку приведем в компактном векторно-матричном виде
где предполагается, что х и с – вектора размерности n; A – матрица размерности m×n; D – матрица размерности n×n. Задачи квадратичного программирования хорошо изучены и существуют достаточное количество эффективных методов их решения [25, 26, 37]. Здесь можно отметить несколько направлений, основанные на обобщении симплекс-алгоритма (например, методы Била, Баранкина – Дорфмана), на условиях Куна и Таккера (например, метод Франка – Вульфа) или на функции Лагранжа.
В.2.3.3. Выпуклое программирование
Задача оптимизации относится к выпуклому программированию, если множество ее допустимых решений Х выпукло, а целевая функция вогнута на Х. Форма записи выражений для множества допустимых 13 решений Х и самой задачи выпуклого программирования совпадают с выражениями (В.7) и (В.8) с учетом того, что функция f(x) должна быть выпуклой, а функции gi (x) линейными и (или) выпуклыми. Для задач выпуклого программирования также разработано значительное число достаточно эффективных методов их решения. Среди них можно отметить методы возможных направлений, впервые предложенные Зойтендейком [84], метод проекции градиента, методы штрафных функций и другие.
В.2.3.4. Нелинейное программирование
Пока не существуют общие аналитические методы решения задач нелинейного программирования, не относящиеся к классу задач квадратичного или выпуклого программирования. Существующие численные методы также не являются универсальными и рассчитаны на использование предшествующей информации для построения улучшенных решений задачи при помощи итерационных процедур. Здесь можно отметить несколько крупных направлений, основанных на принципах: линейной аппроксимации, штрафных функций и возможных направлений

Слайд 11КАРЛ ТЕОДОР ВИЛЬГЕЛЬМ ВЕЙЕРШТРАСС
Карл Теодор Вильгельм Вейерштрасс (1815–1897), немецкий математик.
Исследования Вейерштрасса существенно обогатили математический анализ, теорию специальных функций, вариационное
исчисление, дифференциальную геометрию и линейную алгебру. Вейерштрасс завершил построение фундамента математического анализа, прояснил тёмные места, построил ряд доказательных контрпримеров (аномальных функций), например, всюду непрерывную, но нигде не дифференцируемую функцию Родился в Остенфельде, предместье Эннигерло, в семье чиновника. В 1834 году окончил с отличием гимназию в Падерборне и, по настоянию отца, поступил на юридический факультет Боннского университета. Проучившись 4 года, в течение которых вместо юриспруденции Вейерштрасс усиленно занимался математикой, он бросил университет и поступил в университет Мюнстера. 1840 – подготовил экзаменационную работу по теории эллиптических функций, в которой уже содержатся зачатки его будущих открытий. 1841 – в новой работе Вейерштрасс установил: если последовательность аналитических функций, равномерно сходится внутри некоторой области (то есть в каждом замкнутом круге, принадлежащем области), то предел последовательности – тоже функция аналитическая. Здесь ключевым условием является равномерность сходимости; это понятие и строгая теория сходимости стали одним из важнейших вкладов Вейерштрасса в обоснование анализа. 15 1842 – по окончании Академии получает место учителя в провинциальной католической прогимназии, где проработал 14 лет. Навыки учителя в дальнейшем помогли Вейерштрассу стать лучшим преподавателем Германии, а редкое свободное время (чаще всего ночное) он использовал для математических исследований. Кроме математики, он вёл там занятия по физике, ботанике, географии, истории, немецкому языку, чистописанию и гимнастике. 1854 – публикует статью по абелевым функциям, за которую Кёнигсбергский университет сразу присуждает ему степень почётного доктора без защиты диссертации. Дирихле присылает восторженный отзыв, благодаря которому Вейерштрасс получает звание старшего учителя и давно просимый годичный отпуск. Александр фон Гумбольдт и Куммер помогли Вейерштрассу устроиться профессором сначала Промышленного Института в Берлине, а через пару месяцев – экстраординарным профессором Берлинского университета. Одновременно он избран членом Берлинской Академии наук. Берлинскому университету он отдал 40 лет жизни. С конца 1850-х годов международная известность Вейерштрасса быстро растёт. Этим он обязан великолепному качеству своих лекций. Вот список тематики его курсов: – Введение в теорию аналитических функций, включающее теорию действительных чисел. – Теория эллиптических функций, приложения эллиптических функций к задачам геометрии и механики. – Теория абелевых интегралов и функций. – Вариационное исчисление. Здоровье Вейерштрасса оставляет желать лучшего – сказывается постоянное переутомление в молодые годы. В 1861 году во время выступления у него начался сильный приступ головокружения. и пришлось прервать лекцию. Больше Вейерштрасс никогда не читал лекции стоя – он неизменно сидел, а один из лучших студентов писал за него на доске. 1861 – избран членом Баварской академии наук. 1864 – назначен ординарным профессором. 1868 – избран членом-корреспондентом Парижской академии наук. 1870 – знакомится с двадцатилетней Софьей Ковалевской, приехавшей в Берлин для подготовки диссертации. Нежное чувство к своей Sonja Вейерштрасс пронёс сквозь всю жизнь (он так и не женился). Вейерштрасс помогает Ковалевской выбрать тему диссертации и метод подхода к решению, в дальнейшем регулярно консультирует её по сложным вопросам анализа, содействует в получении научного признания. 16 После защиты диссертации Ковалевская уехала, на письма учителя отвечала редко и неохотно, за исключением ситуаций, когда ей срочно требовалась консультация. 1873 – избран ректором Берлинского университета. 1881 – избран членом Лондонского королевского общества. 1897 – после продолжительной болезни Вейерштрасс скончался от осложнений после гриппа. В его честь был назван кратер Вейерштрасс на Луне. Имя Вейерштрасса носит математический институт в Берлине (WIAS)

Слайд 12I. КЛАССИЧЕСКИЕ МЕТОДЫ ОПТИМИЗАЦИИ
1.1. Общая постановка
Предметом классических методов оптимизации являются
задачи нахождения значений некоторых переменных, подчиненных (условная оптимизация) или не
подчиненных (безусловная оптимизация) системе ограничений в виде равенств, при которых достигается максимальное или минимальное значение целевой функции. Целевая функции и функции, определяющие ограничения, должны быть непрерывными и дифференцируемыми. Других ограничений, включая не отрицательность переменных, на характер функций не предполагается. Математическая модель такой задачи может быть представлена в векторной форме
где x = (x1 , x2 , …, xn ); b = (b1 , b2 , …, bm) или в скалярной форме
Предполагается, что n > m. Разность (n – m) – это число степеней свободы. Пересечение этих m уравнений образует допустимое множество решений
Для данной постановки, согласно теореме Вейерштрасса [15, 41], оптимальное решение существует, если целевая функция непрерывна и множество допустимых решений является компактом и непустым. Рассмотрение классических методов оптимизации начнем с метода безусловной оптимизации.

Слайд 131.2. Метод безусловной оптимизации
Задачу безусловной оптимизации получим из (1.2)
приняв m = 0. В начале также предположим, что число
переменных n = 1, что соответствует одномерной задаче максимизации целевой функции от скалярного аргумента. Тогда имеем
Если x* – точка локального максимума f(x), то очевидно
где x – малое приращение аргумента. Учитывая, что f(x) непрерывная функция разложим ее в ряд Тейлора
которое должно выполняться для любого произвольно малого приращения x. Если x больше нуля, то разделив обе части на x > 0 и переходя к пределу x → 0 получим
Аналогично при x < 0 приходим к
Тогда в качестве необходимого условия получаем, что первая производная в точке локального максимума равна нулю
Поэтому из выражения (1.6) учитывая, что (x)2 всегда положительное число, приходим к необходимому условию, что в точке локального максимума вторая производная отрицательна или равна нулю
Очевидно, достаточным условием строгого локального максимума будет
Геометрическая интерпретация изложенных выкладок показана на рис. 1.1. [15]
Слайд 14Геометрическая интерпретация изложенных выкладок показана на рис. 1.1. [15]
Как видно
из рисунка, угловой коэффициент касательной к кривой f(x) в точке
х = x* равен нулю, причем величина углового коэффициента убывает. Следовательно, по условию (1.9) точка х = x* соответствует строгому максимуму. А в точках х = x** и х = x*** условие второго порядка нарушено, т.е. угловой коэффициент касательной к кривой f(x) в первом случае возрастает, а во втором остается постоянным. Общую задачу безусловной оптимизации при n > 1
можно исследовать по аналогии c одномерным случаем, рассмотренным выше.
Допустим, что локальный максимум существует в точке x* , следовательно где h – малое положительное число, а x определяет некоторое направление в Еn.Рассматривая функцию в правой части неравенства (1.11) как функцию от h разложим ее по формуле Тейлора в окрестности точки h = 0
где G(x* ) – матрица Гесса размерности n ×n с элементами . Сопоставляя выражения (1.12) и (1.11) получим основное неравенство для многомерной задачи безусловной оптимизации, которое должно выполняться для всех направлений x и для всех малых положительных чисел h.
Чтобы вывести из основного неравенства необходимое условие первого порядка, разделим обе части (1.13) на h и перейдем к пределу при h стремящемся к нулю. В итоге получаем, что в точке локального максимума (стационарная точка) градиент функции равен нулевому вектору
![ПРИКЛАДНЫЕ МЕТОДЫ ОПТИМИЗАЦИИ Геометрическая интерпретация изложенных выкладок показана на рис. 1.1. [15]Как видно из Геометрическая интерпретация изложенных выкладок показана на рис. 1.1. [15]Как видно из рисунка, угловой коэффициент касательной к кривой](/img/tmb/4/316904/3068d767304b82d14bd7d317c3875863-800x.jpg)
Слайд 15Из основного неравенства также следует, что в точке локального максимума
матрица Гессе отрицательно определена или отрицательно полу определена
для всех x. Очевидно, что для достижения строгого локального максимума выполняется условие . Для конкретности покажем эти условия на функции двух переменных
Напишем условия первого порядка существования локального максимума
Необходимые условия второго порядка – это отрицательная определенность или отрицательная полуопределенность матрицы Гессе, а это эквивалентно выполнению условий
Если в стационарной точке и если выполнено условие (1.18), то x* будет точкой локального минимума, если (1.18) не выполнено, то x* будет седловой точкой.
Пример 1.1 [19]
Напишем условия первого порядка существования локального экстремума Решая эту систему уравнений получим стационарную точку
Для установления типа экстремума воспользуемся условиями второго порядка (1.17) и (1.18)
Следовательно, функция f(x) в точке (4, 6) достигает максимума.
Слайд 161.3. Классический метод условной оптимизации
Классический метод условной оптимизации применяется
в случаях, когда целевая функция задачи оптимизации по меньшей мере
дважды непрерывно дифференцируема, а ограничения не слишком сложны. Здесь возможны два подхода. Первый, прямое использование аппарата дифференциального исчисления для нахождения стационарных точек целевой функции, как это было рассмотрено выше и исследование этих точек на соответствие ограничениям задачи, а второй – преобразование целевой функции задачи так, чтобы она снова стала задачей безусловной оптимизации. Здесь наибольшее распространение получил метод множителей Лагранжа.
1.3.1. Применение аппарата дифференциального исчисления
Математическая постановка классической задачи условной оптимизации в скалярной форме имеет вид
Учитывая, что применение аппарата дифференциального исчисления для безусловной оптимизации нами подробно рассмотрено в разделе 1.2, представим его в виде укрупненного алгоритма, состоящего из следующих шагов: Шаг 1. По необходимым условиям (1.14) существования экстремумов первого порядка находим все стационарные точки целевой функции задачи. Шаг 2. При задании конкретного типа экстремума, например, максимума с помощью условий второго порядка (1.15) определяем, какие из стационарных точек являются кандидатами на максимум. Шаг 3. Находим максимальные значения целевой функции, достигаемых на каждой границе допустимого множества. Шаг 4. Сравнение значений в стационарных точках, являющимися кандидатами на максимум с максимальными значениями целевой функции, достигаемых на каждой границе допустимого множества. Трудности, связанные с этим методом, состоят в том, что может оказаться несколько стационарных точек и много участков границ, которые нужно проверить; нахождение же экстремальных точек и максимума на каждой границе может потребовать решения систем нелинейных уравнений со всеми вытекающими отсюда неудобствами. Из-за этих трудностей классические методы приходится приспосабливать к каждой задаче индивидуально. Поэтому невозможно, используя дифференциальное исчисление, построить универсальный метод для решения широкого класса общих задач оптимизации. Однако есть и определенное достоинство этого подхода, оно заключается в том, что можно решать условную задачу оптимизации с неотрицательными переменными и при снятии требования, чтобы ограничениями были только равенства, т.е. они могут быть и неравенствами.

Слайд 17Пример 1.2 [19]. Пусть необходимо найти максимум функции
при условиях
В силу
линейности ограничений область допустимых решений Х является выпуклой. Так как
целевая функция непрерывна при всех вещественных значениях переменных, а допустимая область замкнута и ограничена, то по теореме Вейерштрасса существует максимум целевой функции внутри или на границе Х. В соответствии с приведенным выше обобщенным алгоритмом на первом шаге находим стационарную точку целевой функции задачи. Так как эта целевая функция была подробно рассмотрена в разделе 1.2 значение стационарной точки приведем без повторного вычисления: x1 = 4; x2 = 6; max f = 80. Результаты вычислений на шаге 2 также известны из раздела 1.2
Таким образом, целевая функция всюду вогнута. Проверим является ли найденная стационарная точка кандидатом на максимум. Подставив ее значение в ограничения задачи видим, что нарушено третье ограничение и она не является допустимой. Поэтому в соответствии с шагом 3 проверим значения целевой функции на каждой границе.
а) x1 = 0. При этом условии задача примет вид
Из двух последних ограничений следует, что x2 [0; 8]. Далее повторив для этой задачи шаги 1 и 2 получим условия первого и второго порядков 20 – 4x2 = 0, G = –4 < 0. Следовательно x2 = 5; max f = 50
![ПРИКЛАДНЫЕ МЕТОДЫ ОПТИМИЗАЦИИ Пример 1.2 [19]. Пусть необходимо найти максимум функциипри условияхВ силу линейности Пример 1.2 [19]. Пусть необходимо найти максимум функциипри условияхВ силу линейности ограничений область допустимых решений Х является](/img/tmb/4/316904/09ae712111af382022cb6d0fd8068d9c-800x.jpg)
Слайд 18б) x2 = 0. При этом условии задача примет вид:
Здесь
существенным является только первое ограничение, откуда определяется верхняя граница значения
x1 [0, 7], а остальные ограничения излишни. Применение условий первого и второго порядков определения стационарной точки приводит к результату 10 – 4x1 = 0; G(x1 ) = –4 < 0; x1 = 2,5; max f = 12,5
в) x1 = 7. В этом случае задача имеет вид
И, соответственно, из условий первого и второго порядков имеем 27 – 4x2 = 0; G(x2 ) = –4 < 0, имеем x2 = 1, max f = –3.
г) 8 – x1 – x2 = 0. Это равенство позволяет подстановкой x2 = 8 – x1 свести задачу к задаче с одной переменной
Таким образом, из условий 30 – 10x1 = 0; G(x1 ) = –10 < 0 получим значение последней точки-претендента: x1 = 3; x2 = 5; max f = 77. И наконец, сравнивая значения целевой функции вдоль каждой границы убеждаемся, что максимальное ее значение равно f = 77, а оптимальным решением исходной задачи является
Слайд 191.3.2. Метод множителей Лагранжа
Этот метод применяется к классическим задачам
оптимизации с ограничениями –равенствами
f(x) → extremum при g(x) =
b. Суть метода множителей Лагранжа заключается в переходе из задачи с ограничениями к задаче безусловной оптимизации введя специальную функцию Лагранжа:
или в скалярной форме
Находим частные производные функции Лагранжа
Решением этой системы n + m уравнений являются все стационарные точки задачи. Дальше исследование найденных точек осуществляется так же, как и в случае безусловной оптимизации
1.3.3. Обобщенный метод множителей Лагранжа
Дана задача нахождения максимума (для конкретности) функции f(x) при ограничениях gi (x) 0, i = 1, 2, …, m. Ограничения x 0, если таковые имеются, предполагаются включенными в состав m ограничений. Идея метода заключается в том, что если решение безусловной задачи не выполняется для всех заданных ограничений, то условный оптимум должен находиться в граничной точке допустимой области. Это означает, что одно или несколько ограничений из m должны выполняться как равенства. Тогда алгоритм будет состоять из следующих шагов [37]: Шаг 1. Решить задачу безусловной оптимизации заданной целевой функции и решение проверить по всем m ограничениям. Если ограничения не нарушаются, то оптимальное решение найдено. В противном случае принять k = 1 и перейти к шагу 2. Шаг 2. Сделать любые k ограничений равенствами и найти оптимум по методу множителей Лагранжа. Если полученное решение будет допустимым по отношению к остальным ограничениям, то оптимальное решение найдено. Если нет, то активными надо сделать k = k + 1 ограничений и повторить шаг 2. Шаг 3. Если k = m – прекратить вычисления, так как допустимых решений нет.

Слайд 20Контрольные вопросы и упражнения
1. При каких условиях, накладываемых на
допустимое множество ограничений непрерывная целевая функция достигает глобального экстремума?
2.
Какая точка называется стационарной?
3. Если в стационарной точке матрица Гессе является положительно определенной, то в этой точке имеет место максимум или минимум?
4. Если в стационарной точке матрица Гессе оказывается неопределенной, то соответствует ли эта точка экстремуму функции?
5. Для чего предназначен метод множителей Лагранжа?
6. Найдите значение максимума и минимума функции
7. Покажите, что функция f = (x1 – a)2 + (x2 – b)2 + (x3 – c)2 имеет минимум в точке (а, b, c).
Найдите экстремум функции
9. Покажите на графике допустимое множество для классической задачи максимизации с двумя переменными и одним ограничением, где в качестве ограничений берутся следующие соотношения: a) x1 = 10; b) 2x1 + 4x2 = 8; c) (x1 – 1)2 + (x2 – 6)2 = 0.
10. Найдите минимум функции при ограничениях x1 + x2 = 4.
11. Найдите экстремум функции f = x1 x2 x3 при ограничениях x1 + x2 + x3 = 5; x1 x2 + x2 x3 + x1 x3 = 8
12. Найдите максимум функции f = –(2x1 – 5)2 – (2x2 – 1)2 при ограничениях x1 + 2x2 2, x1 , x2 0 с помощью обобщенного метода множителей Лагранжа.

Слайд 21ДЖОРДЖ БЕРНАРД ДАНЦИГ
Джордж Бернард Данциг (8 ноября 1914–13 мая 2005)
– американский математик, из - вестен как разработчик ал го-
ритма, применяемого в ре шениях задач симплекс-мето дом. Считается основоположником линейного программирования, наряду с Леонидом Канторовичем и фон Нейманом. Джордж Бернард Данциг родился в Портленде (США), в семье еврейских эмигрантов из Лодзи. Его отец, Тобиас Данциг был математиком и учился в Париже у Анри Пуанкаре. Тобиас женился на студентке Парижского университета Ане Гитле Урысон и в 1910 году супруги эмигрировали в США. Первое время семья проживала в Портленде. Но в начале 1920-х годов Данциги переехали в Балтимор, а затем в Вашингтон, где Анна стала лингвистом в Библиотеке конгресса, а Тобиас начал преподавать математику в Мэрилендском университете в Колледж-Парке. Джордж посещал Powell Junior High School и Central High School и был в восторге от геометрии. Отец поддерживал увлечённость сына, давая ему сложные геометрические задачи. Джордж Данциг получил степень бакалавра в области математики и физики в Мэрилендском университете (1936), а также степень магистра математики в Мичиганском университете (1938). После двух лет работы в Бюро трудовой статистики Министерства труда США он поступил на докторскую программу в области математики в Калифорнийский университет в Беркли, где изучал статистику под 29 руководством математика Ежи Неймана. Однажды в 1939 году он опоздал на занятия и ошибочно подумал, что написанные на доске уравнения – это домашнее задание. Оно было трудным, но всё-таки Джордж сумел его выполнить. Оказалось, что это были две нерешённые проблемы статистики, с которыми маститые учёные не могли справиться в течение многих лет. Эта история стала очень популярной, обросла легендами и была использована в первых кадрах фильма «Умница Уилл Хантинг». С началом Второй мировой войны Джордж взял отпуск от докторской программы и приступил к работе в Учреждении статистического управления ВВС США. В 1946 году он вернулся в Беркли, в университет, и в том же году получил степень доктора философии по математике. В 1952 году Данциг поступил на работу в математическое подразделение корпорации RAND. В 1960 году он стал профессором факультета промышленной инженерии Калифорнийского университета в Беркли, где основал исследовательский центр, которым руководил в дальнейшем. В 1966 году он перешёл в Стэнфордский университет на должность профессора математических методов исследования операций и информатики. В 1973 году Данциг основал лабораторию оптимизации систем (англ. Systems Optimization Laboratory, SOL), которой заведовал на протяжении длительного времени. В том же году, находясь в творческом отпуске, он возглавил методологическую группу Международного института прикладного системного анализа (МИПС) (Лаксенбург, Австрия). Он активно занимался научной работой и даже после официального выхода на пенсию (1985) преподавал в университете (до 1996 года), готовил к публикации четырёхтомное издание по линейному программированию. Данциг умер в своей университетской квартире (Станфорд, Калифорния), в возрасте 90 лет. Это случилось 13 мая 2005 года. Причиной смерти послужили диабет и заболевания сердца и сосудов. В 1979 году Общество математического программирования ( Mathematical Programming Society, MPS) и Общество промышленной и прикладной математики ( Society for Industrial and Applied Mathematics, SIAM) учредили премию Данцига ( The Dantzig Prize), которую вручают каждые три года, начиная с 1982, за оригинальные исследования, внёсшие выдающийся вклад в математическое программирование [8].

Слайд 22II. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ
2.1. Структура задач и основные положения линейного программирования
Задачи линейного программирования, сформулированные при рассмотрении большинства прикладных задач оптимизации
в экономике, производстве и в других сферах деятельности человека имеют, в общем виде, следующую математическую формулировку: Найти максимум целевой функции при соблюдении ограничений
Эти выражения в более компактной матричной форме имеют вид
где х = (x1 , x2 , …., xn ) и b = (b1 , b2 , …., bm) – вектор-столбцы, с = (c1 , …., cn ) – вектор-строка; А = (aij) – матрица размерности m×n
где Aj – столбцы матрицы А. Решение х является допустимым, если оно принадлежит допустимому множеству Х x X ={x|Ax b, x 0}. Решение x* является оптимальным, если cx* cx для x X, т.е. для всех решений х, удовлетворяющих линейным ограничениям (2.2). Каждое из линейных неравенств системы ограничений определяет замкнутое полупространство и, следовательно, для допустимого множества Х справедлива следующая теорема 2.1 [19] «Допустимое множество Х задачи линейного программирования является замкнутым выпуклым множеством, имеющим не более чем конечное число крайних точек». Следующей важной теоремой линейного программирования является теорема 2.2 «Если целевая функция принимает максимальное значение в некоторой точке допустимого множества Х, то она принимает это максимальное значение в крайней точке допустимого множества Х; если целевая функция достигает максимума более чем в одной крайней точке, то она максимальна в любой выпуклой комбинации этих точек».

Слайд 232.2. Геометрическая интерпретация задачи линейного программирования
Чтобы лучше понять суть
теорем 2.1 и 2.2 рассмотрим простую задачу линейного программирования с
двумя переменными.
На основе общего подхода к оптимизации дифференцируемых функций, рассмотренных ранее, определим градиент целевой функции
На рис. 2.1 заштрихованная площадь является областью допустимых решений Х, а линии уровней расположены перпендикулярно к векторуградиенту. Так как вектор-градиент определяет направление наискорейшего возрастания целевой функции, то по расположению наиболее удаленной линии уровня находим оптимальную точку А с координатами: Данный пример наглядно иллюстрирует правомерность как теоремы 2.1, так и теоремы 2.2. Одновременно, этот пример можно считать Рис. 2.1. Геометрическая интерпретация задачи 32 Д.Н. Шукаев реализацией графического метода решения задачи линейного программирования с двумя переменными.
Слайд 242.3. Симплекс-алгоритм
Как было отмечено во введении учебника для решения
задач линейного программирования был разработан симплекс-метод, основой которого является симплекс-алгоритм.
Симплекс-алгоритм применяется к задачам линейного программирования, приведенным к канонической форме записи
Задачи линейного программирования, сформулированные в виде (2.1, 2.2) легко привести к канонической форме введя в каждое ограничение свободную переменную х и сделать его строгим равенством. В тех случаях, когда исходная постановка задачи линейного программирования отличается от (2.1, 2.2), т.е. среди ограничений имеются равенства, каноническую форму можно получить исключением каждую из базисных переменных из всех ограничений, кроме одного. Для канонической формы базисным решением является
Так как предполагается, что это базисное решение является также и допустимым, величины xj в (2.6) должны быть неотрицательными. Определение 2.1 [13]. Задача линейного программирования представлена в допустимой канонической форме, если выполнено условие b1 0; b2 0; bm 0. Как следует из теорем 2.1 и 2.2 для поиска оптимального решения задачи линейного программирования достаточно изучение одних только базисных решений, так как каждое базисное допустимое решение соответствует крайней точке, а каждая крайняя точка соответствует базисному допустимому решению.

Слайд 252.3.1. Критерий оптимальности
Каноническая форма позволяет не только сразу же
найти допустимое базисное решение, но и определить будет ли оно
оптимальным. Для этого исследуются коэффициенты целевого уравнения (2.5). Определение 2.2 [13]. Коэффициенты целевого уравнения канонической формы называются относительными оценками, так как их значения будут зависеть от выбора базисного множества переменных. Далее, для изложения симплекс-алгоритма в его оригинальном виде (разработанным его автором Джон Данцигом) рассмотрим задачу минимизации целевой функции. Теорема 2.3 [13]. Базисное допустимое решение является минимальным допустимым решением с общими затратами f, если все относительные оценки неотрицательны cj 0, j = 1, …, n. Следствие. Базисное допустимое решение является единственным минимальным допустимым решением, если cj 0 для всех небазисных решений.
Слайд 262.3.2. Улучшение неоптимального базисного допустимого решения
Если среди относительных оценок
cj канонической формы (2.5) имеются отрицательные, то можно, при условии
невырожденности (когда все bj 0), построить новое базисное допустимое решение с меньшим значением целевой функции чем f = f0 . Это решение может быть получено путем увеличения значения одной из небазисных переменных xs и соответствующего изменения базисных переменных. В качестве xs выбирается переменная с индексом s выбранном из условия cs = min cj < 0. (2.7) Используя каноническую форму (2.4) и (2.5) построим решение, в котором xs принимает некоторое положительное значение, значения всех других небазисных переменных остаются по-прежнему нулями, а базисные переменные, включая и f, преобразуются в зависимости от увеличения xs по формулам
Поскольку cs было выбрано отрицательным, то значение xs нужно сделать как можно большим, чтобы значение f стало как можно меньше. Единственное, что помешает сделать xs бесконечно большим – это то, что одна из базисных переменных может стать отрицательной. Однако если все ais 0, то xs можно брать сколь угодно большим. Следовательно справедлива следующая теорема 2.4 «Если в канонической системе для некоторого s все коэффициенты ais неположительны и cs отрицательно, то можно построить класс допустимых решений, для которого множество значений f не будет ограничено снизу». С другой стороны, если хоть одно из ais положительно, то невозможно бесконечно увеличивать значение xs , потому что как только будет

Слайд 27так xi станет отрицательным. Если ais положителен более чем для
одного i, то наименьшее из таких отношений, номер строки которого
будем обозначать через r, определит наибольшее возможное значение х, и при этом базисные переменные будут неотрицательны. Наибольшим значением xs , допустимым при этом предположении, будет
В случае, когда минимум достигается для нескольких i, выбор r является произвольным. Определение. «Базисное решение является вырожденным, если значение хотя бы одной базисной переменной равно нулю». В этом случае из (2.8) следует, что для некоторого ais > 0 соответствующее значение bi для базисной переменной окажется нулевым, и нельзя увеличить xs так, чтобы базисные переменные остались неотрицательными, и поэтому f не будет уменьшаться. Таким образом, улучшение неоптимального базисного решения констатируется следующей теоремой 2.5 [13] «Если в канонической системе для некоторого s относительная оценка cs отрицательна и по крайней мере один коэффициент ais положителен, то из невырожденного базисного допустимого решения можно построить новое базисное допустимое решение с меньшим значением целевой функции». Новое базисное допустимое решение можно снова испытать на оптимальность, проверив выполнение неравенства
Симплекс-алгоритм состоит в повторении этого цикла снова и снова. Этот процесс заканчивается только тогда, когда получим либо а) множество допустимых решений, для которых f → –; либо б) оптимальное базисное допустимое решение (все cj 0). Теорема 2.6 [13]. «В предположении, что ни на одной итерации нет вырожденности, симплекс-алгоритм закончится за конечное число итераций»

Слайд 282.3.3. Пошаговое описание симплекс-алгоритма
Пусть исходная задача линейного программирования представлена
в канонической форме
Шаг 1. Построим начальную симплекс-таблицу (табл. 2.1).
Шаг 2.
Если все сj 0, то конец – оптимальным решением является базисное решение (2.6); если некоторое значение сj < 0, то выбрать переменную xs , которая будет введена в базисное множество на следующей итерации вместо r-й базисной переменной, так чтобы
Шаг 3. а) Если все ais 0, то конец, множество решений есть: – xs 0 произвольно, базисные переменные равны
– небазисные переменные xj = 0 (j s) удовлетворяют исходной системе и обладает свойством
Слайд 29б) Если какое-то ais > 0, то выбираем r-ю базисную
переменную, чтобы вывести ее в следующей итерации, следующим образом
Шаг
4. Чтобы получить из предшествующей таблицы начальные данные таблицы, описывающей следующую итерацию, умножим каждый элемент выбранной строки r на число, обратное ведущему элементу ars и поместим эти произведения в r-ю строку таблицы для следующей итерации (табл. 2.2). Вводим переменную xs на место переменной xn+r в предыдущей итерации. Чтобы получить элемент, стоящий в i-й строке и j-м столбце в новой таблице, вычтем из соответствующего элемента предыдущей таблицы произведение числа, стоящего в i-й строке и s-м столбце предыдущей таблицы на число, стоящее в r-й строке и j-м столбце новой таблицы
где в соответствии с правилами шага 4:
Слайд 30Пример 2.1
. Шаг 1. Начальная симплекс-таблица имеет вид (табл. 2.3)
Шаг
2. cs = min {–9; –10; –16} = –16. Следовательно,
s = 3.
Шаг 3.
Следовательно r = 2 и ведущий элемент ars = a23 = 8
Шаг 4. Переход к следующей симплекс-таблице (табл. 2.4)
Слайд 31Так как условие теоремы 2.3 не выполнено снова переходим к
шагу 2
Шаг 2. cs = –2.Следовательно s = 2.
Шаг
3.
Шаг 4. Переход к следующей симплекс-таблице (табл. 2.5)
Все относительные оценки в последней симплекс-таблице не отрицательны, следовательно, в соответствии с теоремой 2.3 имеем оптимальное решение:
Слайд 322.4. Двойственная задача линейного программирования
2.4.1. Понятие двойственности в линейном программировании
С
каждой задачей линейного программирования
связана другая линейная задача, называемая двойственной
Первоначальная
задача называется исходной. Для понятия сути этой связи рассмотрим задачу использования некоторых ресурсов b = (b1 , b2 , …, b3 ) для производства n видов продукций [25]. Для производства единицы j-й продукции стоимостью cj расходуется aij единиц i-го ресурса. Необходимо определить какое количество каждого вида продукции необходимо производить, чтобы получить максимальную суммарную стоимость всей продукции. Следовательно, исходная задача линейного программирования, в скалярной форме записи, будет иметь вид
Слайд 33Тогда двойственная к ней задача очевидно будет определять оптимальную цену
у каждого из ресурсов, чтобы при заданных b и с
минимизировать общую стоимость затрат ресурсов
Как видно из рассмотренных задач, между их математическими моделями существует тесная связь. Матрица А системы ограничений исходной задачи является транспонированной матрицей в двойственной задаче. Коэффициенты с целевой функции исходной задачи являются свободными членами ограничений двойственной задачи, а свободные члены b ограничений исходной задачи являются коэффициентами целевой функции двойственной задачи. Учитывая, что имеются несколько постановок задач линейного программирования приведем виды соответствия математических моделей исходной и двойственных задач:
Слайд 34Теоретическим обоснованием связи между исходной и двойственной задачами являются следующие
теоремы :
Теорема 2.7. «Если для некоторых допустимых решений x*
и y* взаимно двойственных задач выполняется равенство f(x* ) = z(y* ), то x* и y* являются оптимальными решениями для этих задач».
Теорема 2.8. «Если целевая функция исходной задачи не ограничена сверху, то двойственная к ней задача не имеет допустимого решения». Практическое значение теорем двойственности состоит в том, что они позволяют заменить процесс решения исходной задачи на решение двойственной, которое в определенных случаях может оказаться более простым. Например, задача, область допустимых значений которой описывается двумя неравенствами, связывающими 7 переменных (m = 2, n = 7), не может быть решена графическим методом. Однако данный метод может быть применен для решения двойственной задачи, которая имеет только две переменные.
Слайд 352.4.2. Связь между решениями прямой и двойственной задач
Пусть прямая задача
имеет вид ;
или в матричной форме
Двойственной для нее будет задача
или
в матричной форме
Каждая из этих задач может быть решена независимо друг от друга. Однако при определении симплекс методом оптимального решения одной из них находится и решение другой задачи.
Слайд 36Предположим, что с помощью симплекс метода найдено оптимальное решение прямой
задачи х* , тогда по теореме 2.7 имеем
Оптимальное решение
в матричной форме имеет вид
где А–1 – обратная матрица к матрице, состоящей из элементов итоговой симплекс-таблицы. Подставляя оптимальное решение в выражение (2.9) получим
де cb – вектор коэффициентов базисных переменных в строке целевой функции, вошедших в оптимальное решение. Тогда оптимальное решение двойственной задачи равен
Проиллюстрируем сказанное на конкретном примере 2.2.
Слайд 37Пример 2.2
Дана задача линейного программирования
Тогда двойственная задача имеет вид
Решая прямую
задачу получим следующую итоговую симплекс-таблицу (табл. 2.6).
Слайд 38Таким образом оптимальным решением исходной задачи будет
А оптимальное решение двойственной
задачи определяется значениями коэффициентов f – cтроки итоговой симплекс-таблицы (табл.
2.6):
Убедимся, что ограничения двойственной задачи выполняются
и что в соответствии с теоремой 2.7 значение целевой функции двойственной задачи совпадает с оптимальным значением целевой функции исходной задачи
Слайд 392.5. Двойственный симплекс метод
Двойственный симплекс метод основан на теории двойственности
и используется для решения задач линейного программирования, свободные члены (bi
, i = 1, 2, …, m), которых могут принимать любые значения, а система ограничений задана неравенствами , , =. В двойственном симплекс методе оптимальное решение получается в результате движения по псевдобазисным решениям к области допустимых решений. Когда полученное решение оказывается допустимым, процесс вычислений заканчивается, так как это решение является оптимальным. Суть симплекс метода поясним, анализируя решение конкретной задачи линейного программирования [37]. Пусть необходимо минимизировать целевую функцию
при ограничениях
С начало необходимо преобразовать все ограничения в неравенства со знаком , а затем ввести дополнительные переменные для перехода из неравенств в равенства. В результате получим f = 2x1 + x2 → max,
Слайд 40Попытка составить для данной задачи начальную симплекс-таблицу приводит к выводу,
что значения дополнительных переменных не обеспечивают получение допустимого базисного решения.
Так как целевая функция подлежит минимизации, а все коэффициенты f – уравнения неположительны, начальное базисное решение:
Начальная симплекс-таблица, соответствующая этому оптимальному, но недопустимому решению имеет вид, приведенной в табл. 2.7
Для выбора следующего базисного решения в качестве исключаемой переменной выбирается наибольшее по абсолютной величине отрицательная базисная переменная (при наличии альтернативы выбирается произвольная). Если все базисные переменные неотрицательные, процесс вычисления заканчивается, так как полученное решение допустимое и оптимальное. Затем в качестве включаемую в базис переменной выбирается переменная из числа небазисных. Для этого вычисляются отношения коэффициентов f – строки к соответствующим коэффициентам строки, принадлежащей исключаемой переменной. Отношения с положительным или нулевым значением знаменателя не учитываются. В задаче минимизации вводимой переменной должно соответствовать наименьшее из указанных отношений, а в задаче максимизации – отношение наименьшее по абсолютной величине (при наличии альтернатив выбор делается произвольно). Если знаменатели всех отношений равны нулю или положительные, задача не имеет допустимых решений. В табл. 2.7 исключаемой переменной является x4 = –6, так как она имеет наибольшее по абсолютной величине отрицательное значение. Отношения, вычисленные для определения новой базисной переменной, приведены в табл. 2.8.

Слайд 41
В качестве исключаемой переменной выбирается x2 , так как этой
переменной соответствует минимальное отношение. Последующее стандартное преобразование симплекс-алгоритма (см. раздел
2.3.3) приводит к следующей симплекс-таблице (табл. 2.9):
Новое решение также оптимальное, но не допустимое (x3 = –1 и x5 =–1). Если в качестве новой исключаемой переменной выбрать (произвольно) x3 , то вводимой в базис переменной будет x1 и в результате имеем следующую симплекс-таблицу (табл. 2.10):
Полученное решение исходной задачи
Слайд 42ЛЕОНИД ВИТАЛЬЕВИЧ КАНТОРОВИЧ
Леони́д Вита́льевич Канторо́вич (1912, Санкт-Петербург –1986, Москва) –
советский математик и экономист, один из создателей линейного программирования. Лауреат
Нобелевской премии по экономике 1975 года «за вклад в теорию оптимального распределения ресурсов». Леонид Канторович был младшим ребёнком в семье врача-венеролога Хаима (Виталия) Моисеевича Канторовича и зубного врача Песи Гиршевны Закс, незадолго до того перебравшихся в Петербург из Вильно. У него был брат Николай (1901–1969), впоследствии известный врач-психиатр, доктор медицинских наук, и сестра Лидия, впоследствии инженер-строитель. В 1926 году в возрасте четырнадцати лет поступил в Ленинградский университет. Окончил математический факультет (1930), учился в аспирантуре университета. С 1930 по 1939 год – преподаватель, затем профессор Ленинградского института инженеров промышленного строительства. В 1934 году стал профессором ЛГУ (в 22 года), в 1935 году ему была присвоена учёная степень доктора физико-математических наук без защиты диссертации. В 1938 году Канторович женился на Наталье Ильиной, враче по профессии. У них родилось трое детей. В 1938 году, консультируя фанерный трест по проблеме эффективного использования лущильных станков, Канторович понял, что дело сводится к задаче максимизации линейной формы многих переменных при наличии большого числа ограничений в форме линейных равенств и неравенств. Он модифицировал метод разрешающих множителей Лагранжа для её решения и понял, что к такого рода задачам сводится колоссальное количество проблем экономики. В 1939 году опубликовал работу «Математические методы организации и планирования производства», в которой описал задачи экономики, поддающиеся открытому 51 им математическому методу и тем самым заложил основы линейного программирования. После 1939 года Канторович согласился заведовать кафедрой математики Военного инженерно-технического университета. Канторович – участник обороны Ленинграда. В годы войны преподавал в ВИТУ ВМФ, после войны возглавлял отдел в Институте математики и механики ЛГУ. Новосибирске, где создал и возглавил Математико-экономическое отделение Института математики СО АН СССР и кафедру вычислительной математики Новосибирского университета. C 1942 года он начал обращаться со своими предложениями в Госплан и в 1943 году его доклад был обсужден на совещании в кабинете председателя Госплана Н.А. Вознесенского, однако метод Канторовича был отвергнут как противоречащий марксовой теории трудовой стоимости (заимствующий вместо этого положения буржуазных теорий). В середине 1948 года по распоряжению И.В. Сталина расчётная группа Канторовича была подключена к разработке ядерного оружия. В 1949 году стал лауреатом Сталинской премии «за работы по функциональному анализу». 28 марта 1958 года избран членом-корреспондентом АН СССР (экономика и статистика). С 1958 года возглавлял кафедру вычислительной математики. Одновременно возглавлял отдел приближённых вычислений Ленинградского отделения Математического института им. Стеклова. Был среди учёных первого призыва Сибирского отделения АН СССР. В период работы в СО АН СССР после доноса партийных экономистов Канторовича поместили в психиатрическую лечебницу, но вмешательство брата – известного психиатра – помогло ему вскоре покинуть больницу. 26 июня 1964 года избран академиком АН СССР (математика). За разработку метода линейного программирования и экономических моделей удостоен в 1965 году вместе с академиком В.С. Немчиновым и профессором В.В. Новожиловым Ленинской премии. С 1971 года работал в Москве, в Институте управления народным хозяйством Государственного комитета Совета Министров СССР по науке и технике. В 1975 году стал лауреатом Нобелевской премии по экономике (совместно с Тьяллингом Купмансом «за вклад в теорию оптимального распределения ресурсов»). Умер в Москве 7 апреля 1986 года, похоронен на Новодевичьем кладбище в Москве [8].

Слайд 43III. ТРАНСПОРТНАЯ ЗАДАЧА
3.1. Структура задачи и основные положения
Транспортная задача первоначально
(1941) была поставлена американским ученым Ф. Хичкоком [60] и детально
разобрана Т. Купмансом [65]. Формулировка ее как задачи линейного программирования и методы решения были даны Л.В. Канторовичем и М.К. Гавуриным [18]. Транспортной задачей называется линейная задача построения схемы перевозок между m заданными пунктами отправления, в которых находятся соответствующие количества однородных грузов ai (i = 1, 2, …, m) и n пунктами назначения, куда эти грузы должны быть доставлены соответственно в количестве bj , (j = 1, 2, …, n). Стоимость перевозки единицы продукции из i-го пункта отправления в j-й пункт назначения равна cij и известна для каждого из m×n возможных маршрутов. Задача заключается в определении таких величин xij для всех маршрутов, при которых суммарная стоимость перевозок была бы минимальной. Предполагается, что соблюдается условие баланса
т.е. общая величина спроса равна общей величине наличной продукции. Если бы этот баланс не соблюдался, то его всегда можно восстановить введя, в зависимости от характера дисбаланса, дополнительный фиктивный пункт отправления или назначения с завышенной стоимостью перевозки. При выполнении условия баланса транспортная задача называется закрытой. Математическая модель закрытой транспортной задачи имеет следующий вид

Слайд 44Как видно из этой модели транспортная задача является задачей линейного
программирования с m + n ограничениями и m×n переменными. Специфичная
структура математической модели транспортной задачи позволили на основе детализации симплексного алгоритма построить более эффективные в вычислительном отношении методы. Учитывая прикладную направленность предлагаемой книги приведем без строгих доказательств ряд теорем, послуживших основой для разработки методов решения транспортной задачи.
Теорема 3.1. [9, 25] «Для любой закрытой транспортной задачи имеется решение».
Действительно приняв за решение задачи
где
видим, что ограничения задачи выполняются
Теорема 3.2. [9] «Если параметры ai и bj целые числа, то в любом решении базисные переменные целые числа». Так как все ограничения транспортной задачи имеют коэффициенты, состоящие только из нулей и единиц, а решение уравнений систем ограничений требует только сложения и вычитания, то очевидно, значения переменных будут только целыми числами
Теорема 3.3. [9] «Для транспортной задачи существует решение, содержащее не более чем m + n – 1 положительных переменных». Очевидность данного утверждения вытекает из того факта, что система ограничений транспортной задачи содержит m + n уравнений, которые не являются независимыми в силу условия (3.1), поэтому невырожденное базисное решение транспортной задачи содержит m + n – 1 положительных значений перевозок x

Слайд 453.2. Нахождение исходного базисного решения
Для транспортной задачи итерационный процесс вычисления
оптимального решения, как и в задачах линейного программирования, начинают с
построения исходного базисного решения. Существуют несколько методов нахождение исходного базисного решения: северо-западного угла, минимальной стоимости, двойного предпочтения и др. [25]. Среди них наиболее предпочтительным является метод минимальной стоимости, а наиболее понятным и простым – метод минимальной стоимости. Метод минимальной стоимости позволяет находить исходное базисное решение более близкое к оптимальному решению и, следовательно, уменьшает число итераций. Алгоритм этого метода состоит из трех шагов
Шаг 1. В таблице стоимостей (табл. 3.1) находят клетку с минимальной стоимостью
Шаг 2. В эту клетку помещают меньшее из чисел ai и bj . Затем из рассмотрения исключают либо строку, соответствующую поставщику, либо столбец, соответствующий потребителю, потребности которого полностью удовлетворены, либо и строку, и столбец, если израсходованы запасы поставщика и удовлетворены потребности потребителя. В зависимости от этих условий меняют величину запаса поставщика или величину спроса потребителя
Шаг 3. Проверяют удовлетворены ли все потребности. Если нет переход на шаг 1.
Шаг 4. Получено исходное базисное решение
Применение метода минимальной стоимости покажем на следующем примере 3.1, исходные данные которого представлены в табл. 3.2.

Слайд 46Здесь число пунктов отправления m = 3, а число пунктов
назначения n = 4. Следовательно, базисное решение задачи определяется числами,
стоящими в 4 + 3 – 1 = 6 заполненных клетках.
Шаг 1. Выбираем в таблице наименьшую стоимость c13 = 1
Шаг 2. Так как a1 < b3 80 единиц продукции помещаем в эту клетку и исключаем из рассмотрения первую строку. Новое значение потребности b3 = 15. В оставшейся таблице стоимостей наименьшей является стоимость c32 = 2. Так как b2 < a3 , 25 единиц продукции помещаем в эту клетку и исключаем из рассмотрения второй столбец и корректируем величину запаса a3 = 85 – 25 = 60. В оставшейся таблице снова выбираем наименьшую стоимость и продолжаем процесс до тех пор, пока все запасы не будут распределены, а потребности удовлетворены. В результате получим исходное базисное решение
Метод северо-западного угла. При нахождении начального базисного решения транспортной задачи методом северо-западного угла на каждом шаге рассматривают первый из оставшихся пунктов отправления и первый из оставшихся пунктов назначения. Заполнение клеток таблицы условий начинается с левой верхней клетки для неизвестного x11 («северо-западный угол») и заканчивается клеткой для неизвестного xmn, то есть идет как бы по диагонали таблицы
Применение метода северо-западного угла покажем на следующем примере 3.2, исходные данные которого представлены в табл. 3.3 и совпадают с условиями примера 3.1.
Здесь также число пунктов отправления m = 3, а число пунктов назначения n = 4. Следовательно, базисное решение задачи определяется числами, стоящими в 4 + 3 – 1 = 6 заполненных клетках.

Слайд 47Заполнение таблицы начинается с клетки для неизвестного x11 («северо-западный угол»).
Необходимо удовлетворить потребности первого пункта назначения за счет запасов первого
пункта отправления. Так как запасы первого пункта отправления больше, чем потребности первого пункта назначения, то x11 = 60 и это значение записывается в соответствующей клетке табл. 3.3 и временно исключается из рассмотрения первый столбец, и при этом запасы первого пункта отправления становятся равными 20. Далее по схеме северо-западного угла рассматриваются первые из оставшихся пунктов отправления и назначения. Оставшиеся запасы первого пункта (20) не покрывают потребности второго пункта назначения. Поэтому x12 = 20 и это значение записывается в соответствующей клетке табл. 3.3 и временно исключается из рассмотрения первая строка, так как запасы первого пункта отправления исчерпаны. Не удовлетворенные потребности второго пункта назначения уменьшаются до 5. Теперь заполняется клетка для неизвестного x22 и т.д.
В результате получим исходное базисное решение:
Слайд 483.3. Нахождение оптимального решения транспортной задачи
Для определения оптимального решения транспортной
задачи также разработаны несколько методов: потенциалов, венгерский и другие, однако
наибольшее распространение получил метод потенциалов. Суть 57 III. Транспортная задача этого метода похожа по принципу на симплекс-метод. С начало определяют допустимое базисное решение (например, методом минимальной стоимости), затем его улучшают до получения оптимального решения. Этот метод основан на следующей теореме 3.4 [21] «Если для некоторого допустимого базисного решения xb = {xij} транспортной задачи существуют такие числа
Что
для всех i = 1, 2, …, m и j = 1, 2, …, n, то xb = {xij} – оптимальное решение транспортной задачи». Числа αi и βj называются соответственно потенциалами пунктов отправления и назначения. Условия (3.2) и (3.3) имеют содержательную интерпретацию. Потенциалы αi и βj можно рассматривать как цены на перевозимую продукцию в пунктах отправления и назначения. Тогда, согласно условию (3.2), для оптимальности решения требуется, чтобы на тех маршрутах, по которым действительно перевозится продукция, его цена в пункте назначения возрастала ровно на цену его перевозки, а в соответствии с условием (3.3) в оптимальном решении цена продукции в пункте назначения не может быть меньше ее цены в пункте отправки с учетом затрат на перевозку. Сформулированная теорема позволяет построить алгоритм определения оптимального решения транспортной задачи. При реализации такого алгоритма переход из одного базисного решения к следующему осуществляется путем построения цикла и сдвига по нему

Слайд 49Определение 3.1. «Циклом в таблице условий транспортной задачи называется ломаная
линия, вершины которой расположены в занятых клетках, а звенья –
вдоль строк и столбцов, причем в каждой вершине цикла встречается ровно два звена, одно в строке, другое в столбце. Если ломаная линия пересекается, то точка самопересечения не является вершиной».
Лемма 3.1. «Для любой свободной клетки можно построить только один цикл»
ин цикл». Лемма 3.2. «Переход из одного базисного решения к следующему осуществляется посредством операции сдвига по циклу».
Правило сдвига по циклу: 1) каждой из клеток, связанных циклом с данной свободной клеткой приписывается определенный знак, причем свободной клетке знак +, а всем остальным клеткам поочередно знаки – и +; 2) в данную свободную клетку переносят меньшее из чисел xij, стоящих в минусовых клетках; одновременно это число прибавляют к числам, стоящим в плюсовых клетках и вычитают из чисел в минусовых клетках. Таким образом меняется свободная клетка и получается новое базисное решение транспортной задачи. При сдвиге число занятых клеток остается постоянным: m + n – 1. Если в минусовых клетках имеется 2 или более одинаковых чисел xij, то освобождается только одна из них, а остальные считаются занятыми (с нулевыми поставками). Таким образом для решения транспортной задачи методом потенциалов необходимо реализовать следующий укрупненный алгоритм.
Шаг 1. Определение базисного решения из m + n – 1 элементов (например, методом минимальной стоимости).
Шаг 2. В соответствии с условием (3.2) теоремы 3.4 определение потенциалов βj и αi для всех пунктов назначения и отправления
Шаг 3. Для каждой свободной клетки вычисление числа γij = βj – αi – cij. Если все γij 0, то в соответствии с теоремой 3.4, решение оптимально, если имеются γij > 0, то переход к новому базисному решению
Шаг 4. Среди положительных γij выбирают максимальное и для свободной клетки, которой оно соответствует, строят цикл пересчета и производят сдвиг по этому циклу. Переход на шаг 2

Слайд 50Для численной иллюстрации метода потенциалов воспользуемся примером, использованным при рассмотрении
метода минимальной стоимости. Базисное решение, найденное в пункте 3.2 равно
и
уже записано в табл. 3.2. Поэтому сразу переходим на шаг 2. Для определения значений потенциалов построим систему уравнений:
содержащую m + n – 1 = 6 уравнений с m + n = 7 неизвестными. Полагая значение одного из потенциалов равным нулю α1 = 0, находим значения всех остальных потенциалов: α2 = –4; α3 = –2; β1 = 0; β2 = 0; β3 = 1; β4 = 4.
Так как среди чисел γij имеются положительные, то полученное базисное решение не является оптимальным и необходимо перейти к новому базисному решению. Поэтому на шаге 4 для свободной клетки с наибольшим значением γ14 = 2 строим цикл пересчета (табл. 3.3) и производим сдвиг по этому циклу на наименьшее число в минусовых клетках, равную 45. Клетка в которой находится это число становится
свободной в новой табл. 3.4.
Слайд 51Для полученного нового базисного решения повторим все выкладки шагов 2
и 3. Так на шаге 2 из шести уравнений
находим: α1
= 0; α2 = –6; α3 = –2; β1 = –2; β2 = 0; β3 = 1; β4 = 2
На шаге 3 определяем значения параметров γ11 = β1 – α1 – c11 = –7; γ22 = β2 – α2 – c22 = 0; γ12 = β2 – α1 – c12 = –8; γ23 = β3 – α2 – c23 = –2
Так как все числа γij не положительны, то в соответствии с теоремой 3.4 полученное решение
Слайд 52ДЖОН ФОН НЕЙМАН
Джон фон Не́йман 1903, Будапешт – 1957, Вашингтон)
– венгероамериканский математик еврейского происхождения, сделавший важный вклад в квантовую
физику, квантовую логику, функциональный анализ, теорию множеств, информатику, экономику и другие отрасли науки. Наиболее известен как человек, с именем которого связывают архитектуру большинства современных компьютеров (так называемая архитектура фон Неймана), применением теории операторов к квантовой механике (алгебра фон Неймана), а также как участник Манхэттенского проекта и как создатель теории игр и концепции клеточных автоматов и внесшего большой вклад в развитие математического программирования. Янош Лайош Нейман родился старшим из трёх сыновей в состоятельной еврейской семье в Будапеште, бывшем в те времена второй столицей Австро-Венгерской империи. Его отец, Макс Нейман имел степень доктора от юриспруденции и работал адвокатом в банке. Мать, Маргарет Канн, была домохозяйкой и старшей дочерью (во втором браке) преуспевающего коммерсанта Якоба Канна. Янош был необыкновенно одарённым ребёнком. Уже в 6 лет он мог разделить в уме два восьмизначных числа и беседовать с отцом на древнегреческом. Янош всегда интересовался математикой, природой чисел и логикой окружающего мира. В восемь лет он уже хорошо разбирался в математическом анализе. В 1911 году он поступил в лютеранскую гимназию. В 1913 году его отец получил дворянский титул, и Янош вместе с австрийским и венгерским символами знатности – приставкой фон к австрийской фамилии и титулом Маргиттаи в венгерском именовании – стал называться Янош фон Нейман. Во время преподавания в Берлине и Гамбурге его называли Иоганн фон Нейман. Позже, после переселения в 1930-х годах в США, его имя на английский манер изменилось на Джон. 63 Фон Нейман был женат дважды. В первый раз он женился на Мариэтте Кёвеши в 1930 году. Брак распался в 1937 году, а уже в 1938 г. он женился на Кларе Дэн. От первой жены у фон Неймана родилась дочь Марина – в последующем известный экономист. Фон Нейман получил степень доктора философии по математике (с элементами экспериментальной физики и химии) в университете Будапешта в 23 года. Одновременно он изучал химические технологии в швейцарском Цюрихе. С 1926 по 1930 год Джон фон Нейман был приват-доцентом в Берлине. В 1930 году фон Нейман был приглашён на преподавательскую должность в американский Принстонский университет. Был одним из первых приглашённых на работу в основанный в 1930 году научно-исследовательский Институт перспективных исследований, также расположенный в Принстоне, где с 1933 года и до самой смерти занимал профессорскую должность. В 1937 году фон Нейман стал гражданином США. В 1938 г. он был награждён премией имени М. Бохера за свои работы в области анализа. Первый успешный численный прогноз погоды был произведен в 1950 году с использованием компьютера ENIAC командой американских метеорологов совместно с Джоном фон Нейманом. В октябре 1954 года фон Нейман был назначен членом Комиссии по атомной энергии, которая ставила своей главной заботой накопление и развитие ядерного оружия. Он был утвержден Сенатом Соединенных Штатов 15 марта 1955 года. В мае он и его жена переехали в Вашингтон, пригород Джорджтаун. В течение последних лет жизни фон Нейман был главным советником по атомной энергии, атомному оружию и межконтинентальному баллистическому оружию. Возможно, вследствие своего происхождения или раннего опыта в Венгрии, фон Нейман решительно придерживался правого крыла политических взглядов. В статье журнала «Жизнь», опубликованной 25 февраля 1957 года, вскоре после его смерти, он представлен приверженцем предупредительной войны с Советским Союзом. В 1970 г. Международный астрономический союз присвоил имя Джона фон Неймана кратеру на обратной стороне Луны. В его память учреждены награды: – Медаль Джона фон Неймана. – Теоретическая премия фон Неймана. – Лекция Джона фон Неймана. Летом 1954 года фон Нейману хирурги поставили диагноз: костная форма рака. Предполагалось, что рак фон Неймана мог быть вызван радиоактивным облучением при испытании атомной бомбы в Тихом океане или, может быть, при последующей работе в Лос-Аламосе, штат Нью-Мексико Через несколько месяцев после постановки диагноза фон Нейман умер в тяжёлых мучениях [8].

Слайд 53IV. ЦЕЛОЧИСЛЕННОЕ ПРОГРАММИРОВАНИЕ
4.1. Постановка задачи и геометрическая интерпретация
Значительное число прикладных
задач математического программирования требуют целочисленного решения, например, задачи распределения транспортных
средств, производства неделимой продукции и др. Задача целочисленного программирования формулируется также, как и задача математического программирования, но с дополнительным требованием целочисленности переменных. Если это требование относится ко всем переменным, то говорят о полностью целочисленных задачах, в противном случае о частично целочисленных задачах. Учитывая, что наиболее изученными являются целочисленные задачи линейного программирования, в дальнейшем под термином целочисленное программирование будем понимать линейные задачи
Задача целочисленного программирования в общем случае имеет следующую математическую формулировку:
– найти максимум целевой функции
– при соблюдениях ограничений
где
Слайд 54Если n1 < n – частично целочисленная, а при n1
= n – целочисленная задача.
В настоящее время существуют достаточно много
методов решения задач целочисленного программирования, которые можно объединить в две группы: методы отсечения и комбинаторные методы. Однако эти методы не обеспечивают желательной эффективности своих вычислительных процедур, что особенно проявляется при увеличении размерности задачи. Но сначала выясним почему нельзя находить решения задачи целочисленного программирования путем округления до ближайших целых чисел решения соответствующей ей задачи линейного программирования. Подтвердим сказанное на конкретном примере:
Если не учитывать условие целочисленности, то оптимальное решение равно:
а с учетом целочисленности:
Чтобы понять суть этой проблемы обратимся к геометрической иллюстрации отличий областей допустимых решений задачи линейного программирования и задачи целочисленного программирования.
Как видно из рис. 4.1 оптимальное решение задачи линейного программирования расположена в точке 1. При округлении значения этого решения получим точку 2, которая очень далека от оптимального целочисленного решения в точке 3

Слайд 554.2. Методы решения задачи целочисленного программирования
Как было отмечено выше существуют
две группы методов решения задач целочисленного программирования. Суть методов отсечения,
указанный впервые в работе Д. Данцига, Д. Фулкерсона, С. Джонсона [53], заключается в следующем. Если в результате решения задачи целочисленного программирования без учета целочисленности, получено не целочисленное решение, то к ограничениям исходной задачи добавляется новое линейное ограничение, обладающее свойствами: 1) полученное нецелочисленное решение ему не удовлетворяет; 2) любое целочисленное решение ему заведомо удовлетворяет. Затем решается полученная расширенная задача, в случае необходимости добавляется еще одно ограничение и т.д. до получения целочисленного решения. Таким образом, решение целочисленной задачи сводится к решению некоторой последовательности обычных задач линейного программирования. Геометрически добавление каждого такого ограничения отвечает проведению гиперплоскости, отсекающей от многогранника решений старую оптимальную точку с дробными координатами, но не затрагивающей ни одной из целочисленных точек этого многогранника. Поэтому они и называются «методами отсечения». Наибольшую известность среди методов отсечения получил метод, предложенный Р. Гомори [59], которому удалось разработать универсальное правило формирования дополнительных ограничений и доказать конечность соответствующего процесса отсечения. Вторая группа методов отличается от первой своим комбинаторным характером, т.е. используют идею перебора. Впервые метод такого рода был предложен в 1960 году в статье А. Лэнд и А. Дойг [67] и в настоящее время известен как метод ветвей и границ. Одним из достоинств этого метода является то, что он позволяет находить не только полностью, но и частично – целочисленные решения. Благодаря этому достоинству и относительной простоте реализации на компьютере он получил наибольшее применение при решении прикладных задач целочисленного программирования. Рассмотрим эти два метода.

Слайд 564.2.1. Метод Р. Гомори
Этот метод применяется для решения задачи целочисленного
программирования (4.1), (4.2), при условии целочисленности всех коэффициентов и правых
частей ограничений задачи. Эти условия не сужают область применения метода, так как вполне выполнимы. Например, [37], ограничение
легко можно записать в виде неравенства
в которой дроби отсутствуют. Необходимость введения требования целочисленности параметров исходной задачи обусловлена следующими соображениями. Из дальнейшего рассмотрения будет видно, что как исходные, так и дополнительные переменные задачи, решаемые методом Р. Гомори, должны быть целочисленными. Между тем, наличие в ограничениях дробных коэффициентов приводит к нарушению целочисленности дополнительных переменных. Перейдем к рассмотрению сути метода. На первом этапе решается задача с ослабленными ограничениями, не содержащими условия целочисленности переменных. Если полученное оптимальное решение оказывается целочисленным, то оно является также решением исходной задачи. В противном случае необходимо ввести дополнительные ограничения, порождающие, вместе с исходными ограничениями, новую задачу линейного программирования, решение которой оказывается целочисленным и совпадает с оптимальным решением исходной целочисленной задачи. Пусть последняя симплексная таблица задачи с ослабленными ограничениями имеет следующий вид:

Слайд 57Здесь xi (i = 1, 2, …, m) – базисные
переменные, а vj (j = 1, 2, …, n) –
небазисные переменные. Пусть i-я строка таблицы соответствует нецелому значению базисной переменной xi . Выразим эту переменную как
где bi – нецелое число. Далее представим правые части в виде
где в квадратных скобках записано наибольшее целое число, которое меньше, чем число внутри скобки. Например, если
b1 = 3/2, то [b1 ] = 1, а di = ½
или если
a11 = –5/2, то [d11] = –3, а d11 = 2/3.
После подстановки (4.4) и (4.5) в (4.3) получим
или
Слайд 58Поскольку все переменные xi и Vj принимают целые значения, правая
часть выражения (4.6) должна быть целочисленной, откуда следует, что левая
часть этого выражения также должна принимать целые значения. Далее, так как
для всех i и j, то
Следовательно, выполняется неравенство
Это означает, что поскольку di < 1.
Так как левая часть этого неравенства должна принимать целые значения, можно записать необходимое условие ее целочисленности как
Это ограничение перепишем в виде равенства
где Si – неотрицательная дополнительная переменная, которая по определению должна принимать целые значения. Такое ограничение-равенство определяет отсечение Гомори для полностью целочисленной задачи. Из симплексной таблицы следует, что Vj = 0 и, следовательно Si = – di , то есть данная компонента решения не является допустимой. Это означает, что полученное ранее решение непрерывной задачи не удовлетворяет новому ограничению. В такой ситуации следует использовать двойственный симплекс-метод (раздел 2.5), реализация которого обеспечивает отсечение некоторой области многогранника решений, не содержащих точек с целочисленными координатами. Преобразуем исходную табл. 4.1 путем приписывания к ней строки и столбца, соответствующих построенному отсечению Гомори для полностью целочисленной задачи. В результате получим новую табл. 4.2.

Слайд 59Если полученное (в результате применения двойственного симплекс-метода) решение является целочисленным,
то процесс решения исходной задачи завершен. В противном случае необходимо
ввести новое отсечение на базе полученной табл. 4.2 и вновь воспользоваться двойственным симплекс-методом. Эта процедура повторяется до тех пор, пока не будет найдено целочисленное решение. Если на некоторой итерации при использовании двойственного симплекс-метода обнаруживается отсутствие допустимого решения, то рассматриваемая задача не имеет допустимого решения. При знакомстве с методом Гомори может сложится впечатление, что размеры симплекс-таблицы неограниченно возрастают по мере добавления новых отсечений. Это не соответствует действительности. Общее число ограничений порожденной задачи не может превышать количества переменных исходной задачи [37]. Таким образом, описанные процедуры решения целочисленной задачи линейного программирования можно формализовать в виде следующего алгоритма.
Шаг 1. Решается исходная целочисленная задача линейного программирования с ослабленным ограничением, то есть без требования целочисленности оптимальных решений, отображаемых в итоговой симплекс-табл. 4.1.
Шаг 2. Проверяется целочисленность оптимальных решений. Если в столбце решений итоговой симплекс-таблицу (табл. 4.1) содержатся только целые числа, то получено оптимальное решение целочисленной задачи линейного программирования. В противном случае переход на шаг 3
Шаг 3. Если в столбце решений содержаться дробные решения, то для выбранного дробного решения формируется уравнение отсечения Гомори (4.7) и это уравнение добавляется в систему ограничений исходной задачи в виде дополнительной Si – строки итоговой таблицы шага 1.
Шаг 4. С помощью алгоритма двойственного симплекс-метода осуществляется переход к следующей симплекс-таблице. Далее возврат на шаг 2. Метод Гомори имеет два недостатка. Первое – ошибки округления, возникающие в процессе вычислений на компьютере, в ряде случаев, приводят к получению неверного (неоптимального) целочисленного решения. Второе – решения, последовательно получаемые в процессе реализации метода, не являются допустимыми, то есть алгоритм не позволяет получить какое-либо целочисленное решение, отличное от оптимального. Это означает, что в случае вынужденного прекращения вычислений до момента окончания процесса решения в памяти компьютера не будет содержаться никакого «приемлемого» целочисленного решения исходной задачи.

Слайд 604.2.1. Метод ветвей и границ
Рассмотрим принцип действия этого метода. Как
и в методе Гомори здесь также вначале решается задача без
учета условия целочисленности. Пусть x* дробное решение этой задачи. Интервал [37]
где квадратная скобка означает операцию выделения целой части, не содержит допустимых целочисленных компонент решения. Поэтому допустимое целое значение должно удовлетворять одному из неравенств
Введение этих условий в задачу с ослабленными ограничениями (т.е. без учета целочисленности) порождает две не связанные между собой задачи. Таким образом исходная задача разветвляется на две подзадачи. Осуществляемый в процессе ветвления (рис. 4.3) учет необходимых условий целочисленности позволяет исключить части многогранника допустимых решений, не содержащие точек с целыми координатами. Затем каждая подзадача решается как задача линейного программирования с целевой функцией исходной задачи. Если полученное решение оказывается допустимым для целочисленной задачи, то оно и будет оптимальным и нет необходимости продолжать «ветвление» подзадачи. В противном случае подзадача в свою очередь должна быть разбита на две подзадачи опять при учете условия целочисленности переменных, значения которых в оптимальном решении не являются целыми. Как только полученное допустимое целочисленное решение одной из подзадач оказывается имеющегося, оно фиксируется вместо зафиксированного ранее. Процесс ветвления продолжается, насколько это возможно, до тех пор, пока каждая подзадача не приведет к целочисленному решению или пока не будет установлена невозможность улучшения имеющегося решения. В этом случае зафиксированное допустимое решение является оптимальным.

Слайд 61С учетом сказанного можно построить следующий укрупненный алгоритм метода ветвей
и границ.
Шаг 1. Решить задачу целочисленного программирования без учета
целочисленности переменных.
Шаг 2. Проверить все ли решения целые: а) если да, то найдено оптимальное решение; б) если нет, перейти на следующий шаг.
Шаг 3. Выбрать любое нецелое решение, округлить до ближайшего целого в меньшую и большую сторону
Шаг 4. Решить полученные две подзадачи
Шаг 5. Выбрать точку ветвления по наилучшему значению целевой функции среди висячих вершин дерева ветвления.
Шаг 6. Проверка для выбранной точки ветвления все ли – целые: а) если да, то получено оптимальное решение; б) если нет, то переход на шаг 3.





![ПРИКЛАДНЫЕ МЕТОДЫ ОПТИМИЗАЦИИ Геометрическая интерпретация теоремы 2 показана на рис. В.2 [15]. Линия (поверхность) Геометрическая интерпретация теоремы 2 показана на рис. В.2 [15]. Линия (поверхность) уровня целевой функции это множество точек](/img/thumbs/130e362a175ccf57b0a945552aac2b98-800x.jpg)







![ПРИКЛАДНЫЕ МЕТОДЫ ОПТИМИЗАЦИИ Геометрическая интерпретация изложенных выкладок показана на рис. 1.1. [15]Как видно из Геометрическая интерпретация изложенных выкладок показана на рис. 1.1. [15]Как видно из рисунка, угловой коэффициент касательной к кривой](/img/tmb/4/316904/3068d767304b82d14bd7d317c3875863-800x.jpg)


![ПРИКЛАДНЫЕ МЕТОДЫ ОПТИМИЗАЦИИ Пример 1.2 [19]. Пусть необходимо найти максимум функциипри условияхВ силу линейности Пример 1.2 [19]. Пусть необходимо найти максимум функциипри условияхВ силу линейности ограничений область допустимых решений Х является](/img/tmb/4/316904/09ae712111af382022cb6d0fd8068d9c-800x.jpg)































































