Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Тема №8 Задача 1 Задача 4 Задача 2 Задача 3 Задача 5 Задача 6 Задача 7 Задача
Содержание
- 1. Тема №8 Задача 1 Задача 4 Задача 2 Задача 3 Задача 5 Задача 6 Задача 7 Задача
- 2. Магнитное полеПо закону Био-Савара-Лапласа элемент контура dl,
- 3. Найти напряженности Н магнитного поля в точке,
- 4. Дано:Решение:а=2 мI=5 А =3,14 Н-? Напряженность магнитного
- 5. Найти напряженность Н магнитного поля в центре
- 6. Дано:Решение:R=0,01 мI=1 А Н-? Вывод данной формулыВ
- 7. На рисунке изображены сечения двух прямолинейных бесконечно
- 8. Дано:Решение:M1А =2 смАМ2=4 смВМ3 = 3 смI1=20
- 9. Н1 и Н2- напряженности магнитных полей, создаваемые
- 10. На рисунке изображены сечения трех прямолинейных бесконечно
- 11. Дано:Решение:x– ? АВ=ВС=5 смI1 = I2=II3 =
- 12. Спроецируем вектора на ось Оу, получаем с
- 13. Спроецируем вектора на ось Оу, получаем с
- 14. Два прямолинейных бесконечно длинных проводника расположены перпендикулярно
- 15. АВ= 0,02 мI1 = 2 AI2=3 AAM1=AM2=10-2
- 16. Ответ: напряженность магнитного поля в точках M1 и M2 соответственно равны Н1=35,6 А/м и Н2=57,4 А/м.
- 17. Два прямолинейных длинных проводника расположены параллельно на
- 18. Дано:Решение:I1 = I2=5 Аа = 0,1 мd=0,l
- 19. Два круговых витка радиусом R=4 см каждый
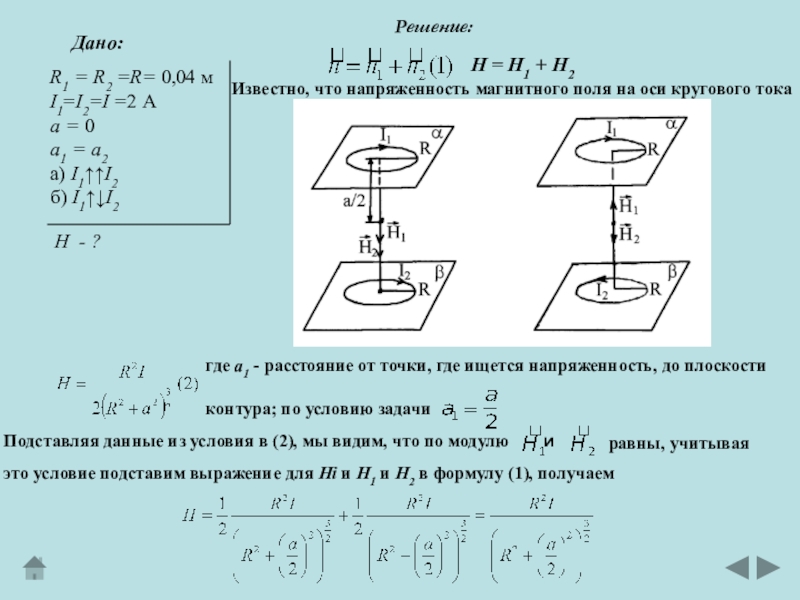
- 20. Дано:Решение:R1 = R2 =R= 0,04 мI1=I2=I =2
- 21. б) Рассмотрим второй случай, когда токи в
- 22. Ток I=20 А идет по длинному проводнику,
- 23. Дано:Решение:I=20 Аr = 0,1 м H -
- 24. Из проволоки длиной L=1 м сделана квадратная
- 25. Дано:Решение:H– ? L=1 мI=10 А По условию
- 26. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2Магнитное поле
По закону Био-Савара-Лапласа элемент контура dl, по которому течет
ток I, создает в
некоторой точке А пространства магнитное поле
напряженностью где r - расстояние от точки А до элемента тока dl,
а - угол между радиус - вектором r и элементом тока dl.
Применим закон Био-Савара-Лапласа к контурам различного вида.
Напряженность магнитного поля в центре кругового тока
R - радиус кругового
контура с током.
Напряженность магнитного поля, созданного бесконечно длинным прямолинейным
проводником
где а - расстояние от точки, где ищется напряженность,
до проводника с током.
Напряженность магнитного
поля на оси кругового тока
где R - радиус кругового контура с током,
а — расстояние от точки до плоскости контура.
Напряженность поля внутри тороида и бесконечно длинного соленоида
Н=Iп,
где п - число витков на единицу длины соленоида.
Напряженность магнитного поля на оси соленоида конечной длины
где 1 и 2- углы между осью соленоида и радиус - вектором,
проведенным из рассматриваемой точки к концам соленоида.
Слайд 3Найти напряженности Н магнитного поля в точке, отстоящей на расстоянии
а=2 м от
бесконечно длинного проводника, по которому течет ток
I=5 А.Условие задачи
Задача №1
Слайд 4Дано:
Решение:
а=2 м
I=5 А
=3,14
Н-?
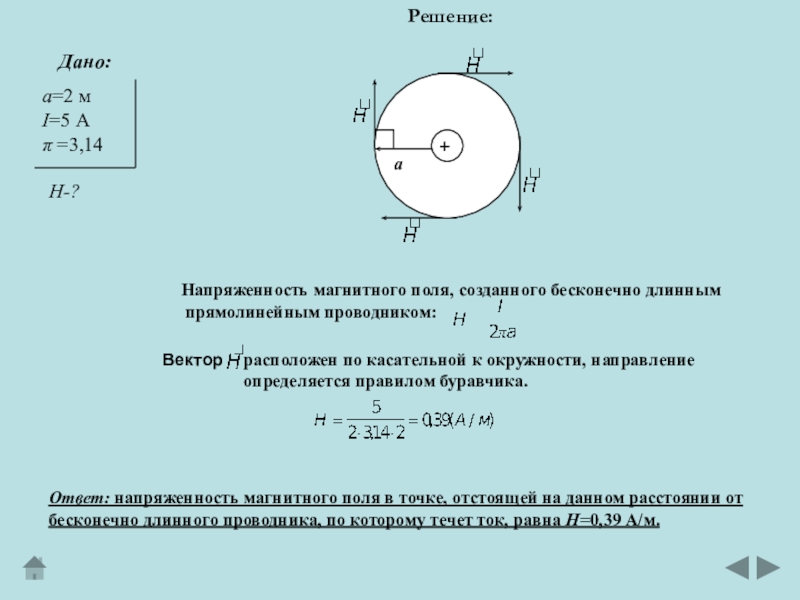
Напряженность магнитного поля, созданного бесконечно
длинным
прямолинейным проводником:
Вектор
расположен по касательной к окружности, направление
определяется правилом буравчика.
Ответ: напряженность магнитного поля в точке, отстоящей на данном расстоянии от
бесконечно длинного проводника, по которому течет ток, равна Н=0,39 А/м.
+
a
Слайд 5Найти напряженность Н магнитного поля в центре кругового проволочного витка
радиусом R=l с которому течет ток I=1 А.
Условие задачи
Задача №2
Слайд 6Дано:
Решение:
R=0,01 м
I=1 А
Н-?
Вывод данной формулы
В этом случае все
элементы проводника перпендикулярны к радиус - вектору и sin =l.
Расстояние всех элементов провода до центра круга одинаково и равно радиусу круга R. Поэтому,
используя закон Био-Савара - Лапласа получаем:
Все элементы тока создают магнитное поле одинакового направления, перпендикулярное к
плоскости витка, и поэтому полная напряженность поля в центре кругового витка равна
где l - длина окружности.
Ответ: напряженность магнитного поля в центре кругового проволочного витка равна 50 А/м.
Слайд 7На рисунке изображены сечения двух прямолинейных бесконечно длинных проводников
с
токами. Расстояние между проводниками АВ=10 см, токи I1=20A и I2=30A.
Найтинапряженность Н магнитного поля, вызванного токами I1 и I2 в точках M1, М2, М3.
Расстояния M1А =2 см, АМ2=4 см, ВМ3 = 3 см.
Условие задачи
Задача №3
Слайд 8Дано:
Решение:
M1А =2 см
АМ2=4 см
ВМ3 = 3 см
I1=20 A
I2=30 A
АВ=10 см
Н1, Н2, Н3-?
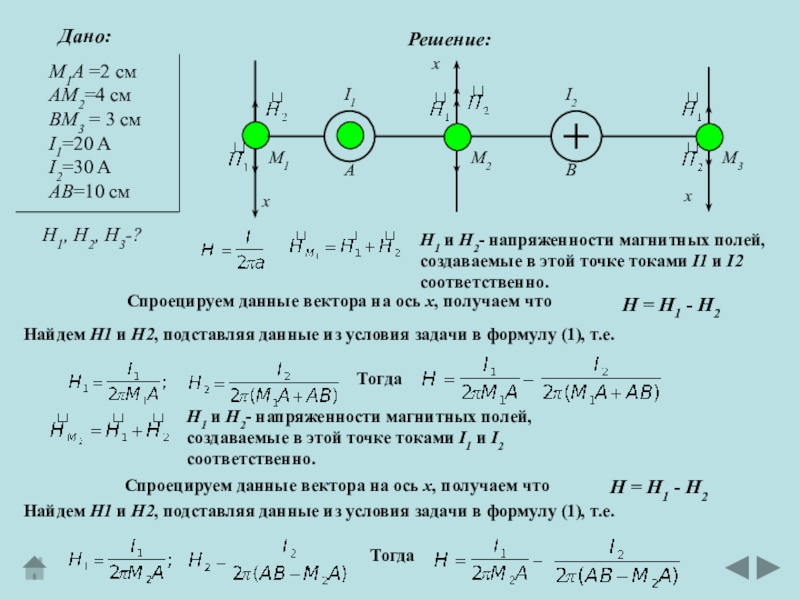
Н1 и Н2- напряженности магнитных полей,
создаваемые
в этой точке токами I1 и I2 соответственно.
Спроецируем данные вектора на ось х, получаем что
Н = Н1 - Н2
Найдем Н1 и Н2, подставляя данные из условия задачи в формулу (1), т.е.
Тогда
Н1 и Н2- напряженности магнитных полей,
создаваемые в этой точке токами I1 и I2
соответственно.
Спроецируем данные вектора на ось х, получаем что
Н = Н1 - Н2
Найдем Н1 и Н2, подставляя данные из условия задачи в формулу (1), т.е.
Тогда
I1
I2
B
A
x
x
x
M3
M2
M1
Слайд 9Н1 и Н2- напряженности магнитных полей,
создаваемые в этой точке
токами I1 и I2
соответственно.
Спроецируем данные вектора на ось х,
получаем чтоН = Н1 - Н2
Найдем Н1 и Н2, подставляя данные из условия задачи в формулу (1), т.е.
Тогда
Ответ: напряженности магнитного поля, вызванного токами I1 и I2 в точках М1, М2, М3
соответственно равны H1=120 А/м, Н2=159 А/м, Н3=135 А/м.
Слайд 10На рисунке изображены сечения трех прямолинейных бесконечно длинных проводников
с
токами. Расстояния АВ=ВС =5 см, токи I1 = I2=I и
I3 = 2I. Найти точку на прямой АС,в которой напряженность магнитного поля, вызванного токами I1, I2и I3, равна нулю.
Условие задачи
Задача №4
Слайд 11Дано:
Решение:
x– ?
АВ=ВС=5 см
I1 = I2=I
I3 = 2I
Hрез = 0
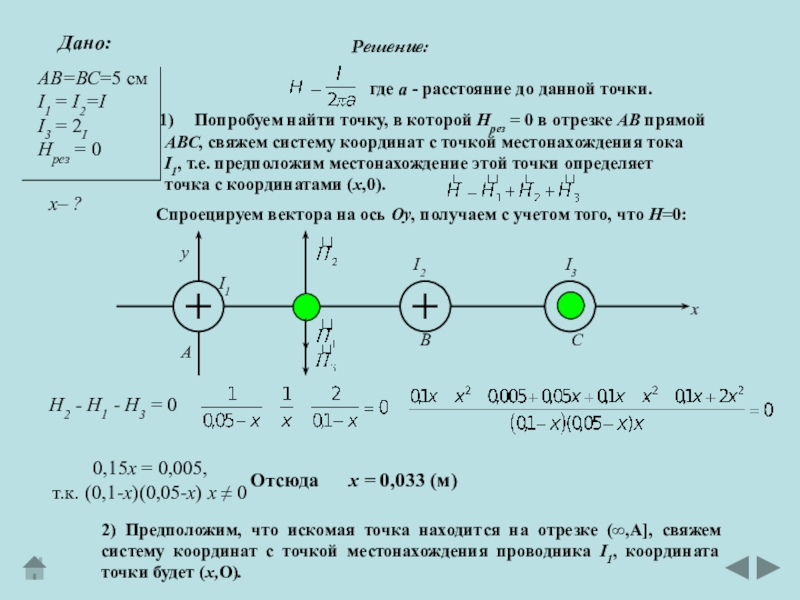
где а - расстояние до данной точки.
Попробуем найти точку,
в которой Hрез = 0 в отрезке АВ прямой АВС, свяжем систему координат с точкой местонахождения тока
I1, т.е. предположим местонахождение этой точки определяет
точка с координатами (х,0).
Спроецируем вектора на ось Оу, получаем с учетом того, что Н=0:
Н2 - Н1 - Н3 = 0
0,15х = 0,005,
т.к. (0,1-х)(0,05-х) х 0
Отсюда
х = 0,033 (м)
2) Предположим, что искомая точка находится на отрезке (,А], свяжем систему координат с точкой местонахождения проводника I1, координата точки будет (х,О).
I1
I2
I3
B
C
A
y
x
Слайд 12Спроецируем вектора на ось Оу, получаем с учетом того, что
Н=0:
Н2 - Н1 + Н3 = 0
-0,15х = 0,005,
т.к. (0,1+х)(0,05+х)
х 0х = -0,033 (м)
3) Предположим, что искомая точка находится на отрезке ВС.
т.к. векторы
и
сонаправлены.
4) Предположим, что искомая точка находится на отрезке [С,), свяжем систему координат
с местонахождением проводника I3 и координата точки будет (х,0).
I1
I2
I3
B
C
A
I1
I2
I3
B
C
A
y
x
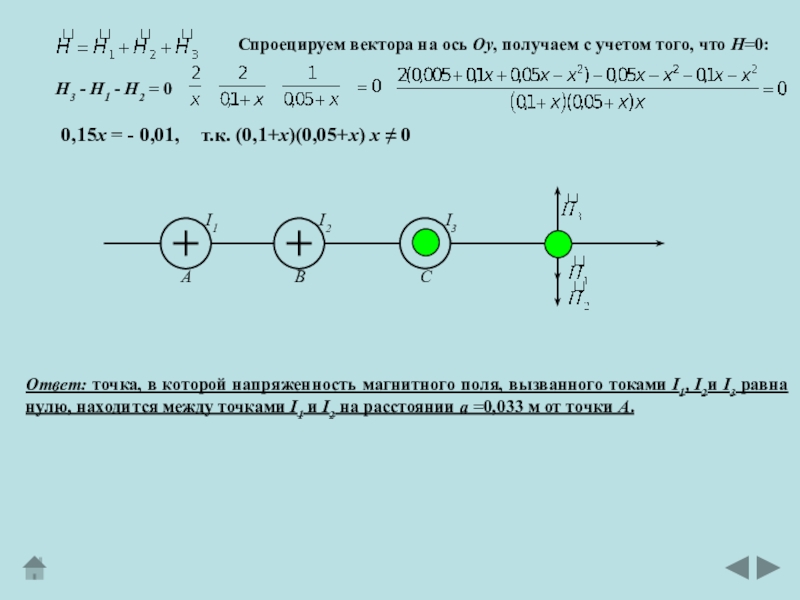
Слайд 13Спроецируем вектора на ось Оу, получаем с учетом того, что
Н=0:
Н3 - Н1 - Н2 = 0
0,15х = - 0,01,
т.к.
(0,1+х)(0,05+х) х 0Ответ: точка, в которой напряженность магнитного поля, вызванного токами I1, I2и I3 равна
нулю, находится между точками I1 и I2 на расстоянии а =0,033 м от точки А.
I1
I2
I3
B
C
A
Слайд 14Два прямолинейных бесконечно длинных проводника расположены перпендикулярно
друг к другу
и находятся во взаимно перпендикулярных плоскостях. Найти
напряженности H1 и
H2 магнитного поля в точках M1 и M2, если токи I1=2 А и I2=3A. Расстояния AM1=AM2=l см и АВ = 2см.
Условие задачи
Задача №5
Слайд 15АВ= 0,02 м
I1 = 2 A
I2=3 A
AM1=AM2=10-2 м
Дано:
Решение:
H1, H2
- ?
или
1) Найдем напряженность H1 в точке M1.
Векторы
напряженности H1 и H2 магнитного поля, вызванного токами I1 и I2находятся во взаимно перпендикулярных плоскостях.
Напряженность магнитного поля,
созданного бесконечно длинным
прямолинейным проводником
где а - расстояние от проводника до
рассматриваемой точки.
2) Найдем напряженность
H2 в точке M2.
Воспользовавшись
формулой (2), найдем
и
Слайд 16Ответ: напряженность магнитного поля в точках M1 и M2 соответственно
равны
Н1=35,6 А/м и Н2=57,4 А/м.
Слайд 17Два прямолинейных длинных проводника расположены параллельно на расстоянии
а=10 см
друг от друга. По проводникам текут токи I1 = I2=5
А в противоположныхнаправлениях. Найти модуль и направление напряженности магнитного поля в точке,
находящейся на расстоянии а=10 см от каждого проводника.
Условие задачи
Задача №6
Слайд 18Дано:
Решение:
I1 = I2=5 А
а = 0,1 м
d=0,l м
AM1=AM2=l0-2 см
H
- ?
и
- напряженности магнитных полей,
созданных бесконечно
длинными проводниками I1 и I2.
где угол = 60°, т.к. DAC=360-60°-290=120, т.к. АВС - равносторонний,
т.к. DAC является прилежащим углом к BCA в параллелограмме ABCD, то
BCA=0,5(360°-240°)=60°
Напряженность магнитного поля, созданного бесконечно длинным проводником:
Используя данную формулу, найдем Н1 и Н2:
Подставим (2), (3) в (1), получаем:
Ответ: модуль напряженности магнитного поля в точке, находящейся на расстоянии а=10 см
от каждого проводника, равна Н=8 А/м. Напряженность магнитного поля направлена
перпендикулярно к плоскости, проходящей через оба провода.
Слайд 19Два круговых витка радиусом R=4 см каждый расположены в параллельных
плоскостях
на расстоянии а=10 см друг от друга. По виткам
текут токи I1=I2=1 А. Найти напряженность Н магнитного поля на оси витков в точке, находящейся на равном
расстоянии от них. Задачу решить, когда:
а) токи в витках текут в одном направлении;
б) токи в витках текут в противоположных направлениях.
Условие задачи
Задача №7
Слайд 20Дано:
Решение:
R1 = R2 =R= 0,04 м
I1=I2=I =2 А
a = 0
a1
= a2
a) I1I2
б) I1I2
H - ?
Н = Н1
+ Н2Известно, что напряженность магнитного поля на оси кругового тока
где a1 - расстояние от точки, где ищется напряженность, до плоскости
контура; по условию задачи
Подставляя данные из условия в (2), мы видим, что по модулю
и
это условие подставим выражение для Hi и Н1 и Н2 в формулу (1), получаем
равны, учитывая
Слайд 21б) Рассмотрим второй случай, когда токи в витках текут в
противоположных направлениях.
результирующий вектор будет равен нулю, т.е.
Н1 - Н2
= 0 и Н = 0Ответ: напряженность магнитного поля на оси витков в точке, находящейся на равном
расстоянии от них, когда:
а) токи в витках текут в одном направлении равна Н=12,2 А/м;
б) токи в витках текут в противоположных направлениях Н=0 А/м.
Слайд 22Ток I=20 А идет по длинному проводнику, согнутому под прямым
углом. Найти
напряженность Н магнитного поля в точке, лежащей на
биссектрисе этого угла и отстоящей от вершины на расстояние r =10 см.
Условие задачи
Задача №8
Слайд 23Дано:
Решение:
I=20 А
r = 0,1 м
H - ?
Векторы напряженности
магнитных полей,
вызванных током I, текущим по отрезкам(-;А]
и [А;+
) соответственно находятся на одной прямой перпендикулярной плоскости, в которой
находятся отрезки данного проводника.
Но
l = a·ctg,
Для первого отрезка, а именно (-;А], углы:1=0°, 2=45°. Для второго отрезка, а именно
[А;+ ), углы: 1=45°, 2=180°.
Н = Н1 + Н2 (2)
Подставляя (1) в (2), получаем при этом замечая, что а - перпендикуляр, проведенный из точки В
на отрезки, для этих отрезков расстояние а одинаково, и может быть найдена по теореме
Пифагора из АВС, учитывая то, что катеты равны по величине и равны а, гипотенуза равна г,
отсюда:
Подставляя сначала (3) в (1), потом (1) в (2), получаем
Ответ: напряженность магнитного поля в точке, лежащей на биссектрисе угла, созданного
длинным прямолинейным проводником, и отстоящей от вершины угла на данное расстояние
равна Н=13,2A/м.
I
r
a
a
l
a
A
l
B
I
Слайд 24Из проволоки длиной L=1 м сделана квадратная рамка. По рамке
течет ток I=10 А.
Найти напряженность Н магнитного поля в
центре рамки. Условие задачи
Задача №9
Слайд 25Дано:
Решение:
H– ?
L=1 м
I=10 А
По условию ABCD - квадрат,
значит
сторона L рамки будет, а длина
перпендикуляра
проведенного из точки О на L сторону квадрата
будет равен а, т.е
Н = Н1 + Н2+ Н3+ Н4=4Н1 (2)
Из ранее полученных формул, с использованием закона Био - Савара - Лапласа найдем Н1:
В нашем случае 1=45°, 2=180°-45°=135°.
Подставим (3) в (2) с использованием отношения (1), получаем
Ответ: напряженность магнитного поля в центре рамки равна Н=35,8 А/м.