Приложение производной к исследованию функции

функции
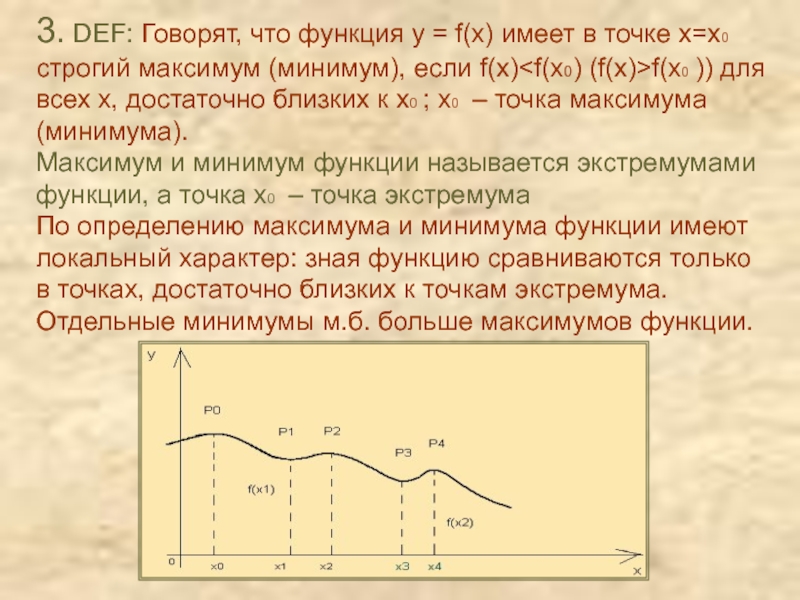
Экстремумы функции
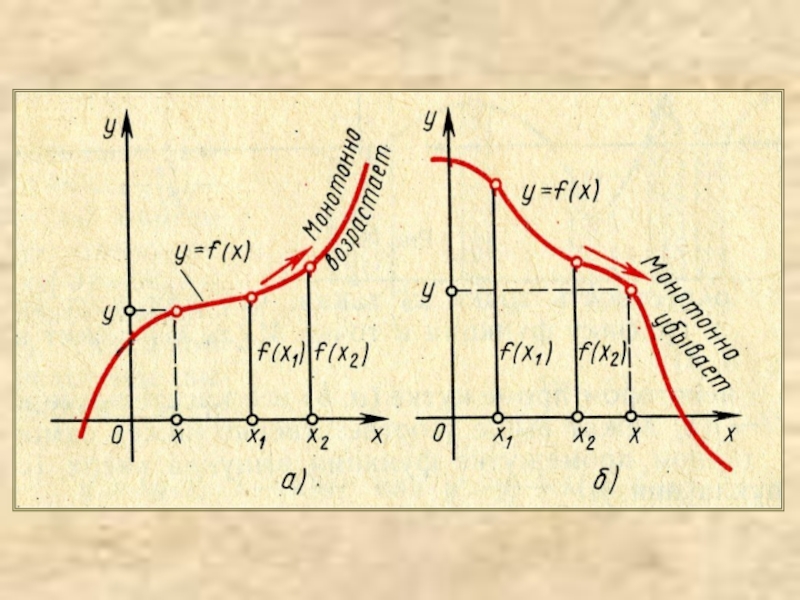
Алгоритм исследования функции на экстремумы и промежутки монотонности
Исследования функции

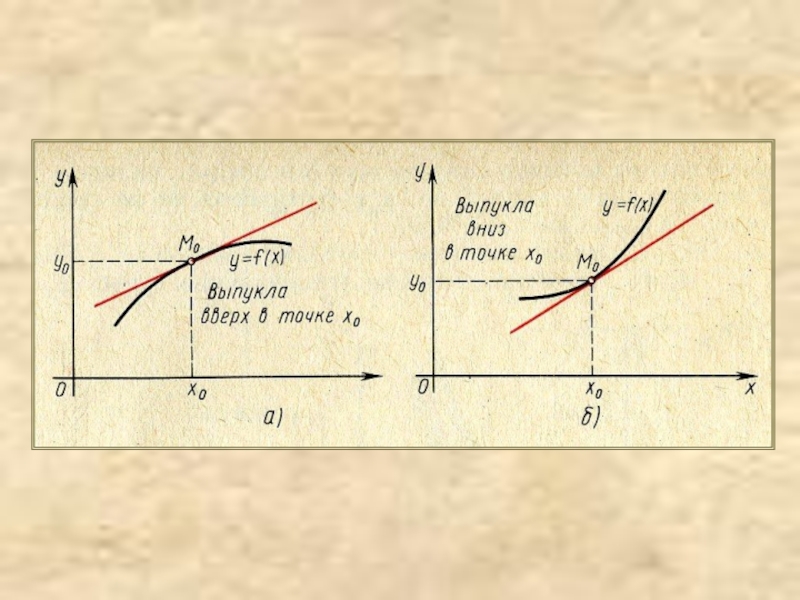
на выпуклость, вогнутость:
Определение выпуклости функции вверх и вниз
Достаточное условие выпуклости функции на интервале
Точка перегиба
Достаточный признак существования точки перегиба
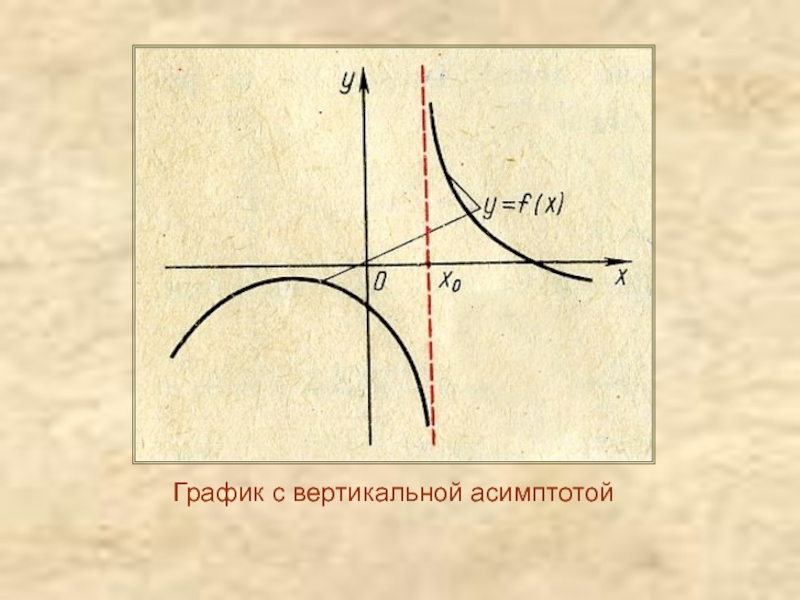
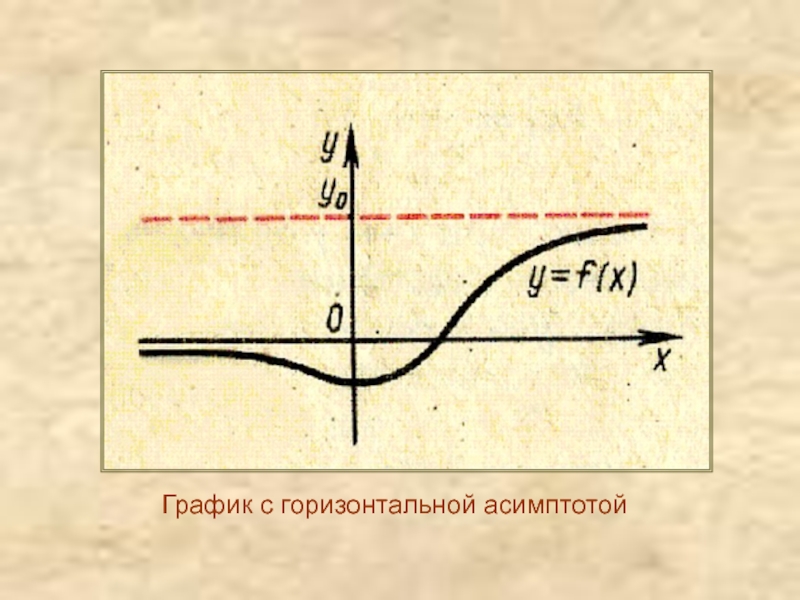
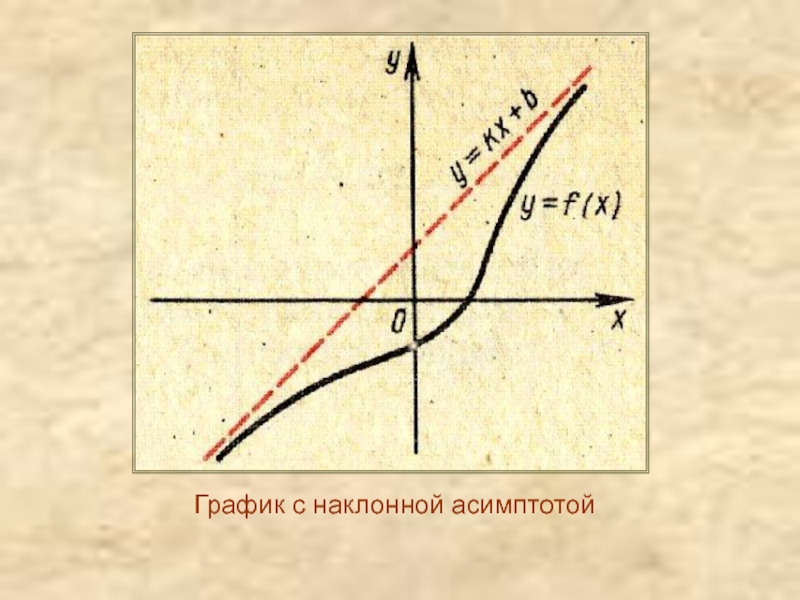
Асимптоты

в одном направлении, т.е. либо только возрастает, либо только убывает.

Очевидно, что движение точки х в сторону положительного направления оси абсцисс является монотонно возрастающим, а в противоположную сторону - монотонно убывающим

возрастающей на интервале (a, b), если для любых х1 и

x2, принадлежащих этому интервалу, из неравенства x2 > х1 сле­дует неравенство f(x2) > f(x1). Функция y = f(x) называется монотонно убывающей на интервале (а, b), если для любых х1 и x2, принадлежащих этому интервалу, из неравенства x2 > x1 следует неравенство f(x2)< f(x1). Естественно, что интервал (a,b) предполагается взятым из области определения функции.

дифференцируемая функция возрастает (убывает) на некотором интервале, то ее производная

неотрицательная (неположительная) на этом интервале.
Th: Если производная функции на некотором интервале положительна (отрицательна), то функция возрастает (убывает) на этом интервале.

точке х=х0 строгий максимум (минимум), если f(x)f(x0 )) для

всех х, достаточно близких к х0 ; х0 – точка максимума (минимума). Максимум и минимум функции называется экстремумами функции, а точка х0 – точка экстремума По определению максимума и минимума функции имеют локальный характер: зная функцию сравниваются только в точках, достаточно близких к точкам экстремума. Отдельные минимумы м.б. больше максимумов функции.

экстремум в некоторой точке, то ее производная в этой точке

равна нулю или не существует.
Th: Пусть функция f(x) непрерывна в некотором интервале, содержащем критическую точку х0, и дифференцируемая во всех точках этого интервала, кроме б.м., самой точки х0.
Если при переходе аргумента слева направо через точку х0 производная f `(x0) меняет знак с плюса на минус, то функция в этой точке имеет максимум; если знак меняется с минуса на плюс, то функция имеет минимум.

f ’(x)
Находим точки, в которых f ’(x)=0 или f’(x)

не существует
Разбиваем этими точками область определения f(x) на промежутки
Методом проб определяем знак f ’(x) в этих промежутках и находим интервалы монотонности
Применяем достаточное условие экстремума.

f(x) выпукла вверх в точке x0, если существует окрестность точки

x0 такая, что для всех ее точек х касательная к графику функции в точке
M0(x0; y0) лежит выше графика.
Говорят, что функция y = f(x) выпукла вниз в точке x0, если существует окрестность точки х0 такая, что для всех ее точек х касательная к графику функции в точке
M0(x0; y0) лежит ниже графика.

II. Исследование функции на выпуклость, вогнутость

не меняет знак на этом интервале, то:
1) при f″(x) >

0 (знак +) функция f(x) выпукла вниз на интервале (a, b);
2) при f″(x) < 0 (знак -) функция f(x) выпукла вверх на интервале (a, b).

2. Достаточное условие выпуклости функции на интервале.

называется точкой перегиба этого графика, если существует такая окрестность точки

x0, в пределах которой график функции y = f(x) слева и справа от M0 имеет разные направления выпуклости.

3.

обращается в нуль или не существует, называется критическими точками 2-го

рода. В этих точках перегиб может быть, а может и не быть.
Если для функции y=f(x) вторая производная ее f”(x) в некоторой точке x0 обращается в нуль и при переходе через точку меняет свой знак на обратный, то точка М(х0; f(x0)) является точкой перегиба функции.

кривой y = f(x) до некоторой определенной прямой при x

→ x0 и неограниченном удалении точки М от начала координат стремится к нулю, то эта прямая называется асимптотой кривой.

x0 – конечное число, то соответствующую асимптоту называют вертикальной. Определение:

Прямая x = a называется вертикальной асимптотой графика функции y = f(x), если хотя бы один из пределов или равен + ∞ или - ∞.

∞, то соответствующая асимптота является либо горизонтальной, либо наклонной. Говорят, что

прямая y = b служит горизонтальной асимптотой для графика функции y = f(x), если Если же равен числу b только один из этих пределов, то прямая y = b является горизонтальной асимптотой соответствующей части графика функции y = f (x), т.е. при x = + ∞ или при x = - ∞.

графика функции y = f(x) при x→ +∞ (соответственно при

х→ -∞), если f(x) представима в виде f(x) = kx + b +α(x), где (соответственно ) Замечание: Если k = 0, то наклонная асимптота превращается в горизонтальную.

на -∞:
у=-х+2
Наклонная асимптота на +∞:

у=х-2

Четность, нечетность функции.
3. Периодичность.
4. Точки пересечения с осями координат.
5.

Монотонность. Экстремумы функции.
6. Точки перегиба. Выпуклость функции.
7. Асимптоты.
8. График.