Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Приложения формулы Тейлора к вычислению пределов
Содержание
- 1. Приложения формулы Тейлора к вычислению пределов
- 2. Вычисление пределов с помощью формулы Тейлора.
- 3. Часто бывает удобно для разложений функций f(x)
- 4. Случай x → ∞ сводится заменой переменной x = 1/t к случаю t → 0. ПРИМЕР 2. положим
- 5. При раскрытии данным методом неопределенностей вида
- 6. Приложения формулы Тейлора к исследованию поведения функции
- 7. Доказательство. Формула Тейлора n-ого порядка для функции
- 8. ПРИМЕР. Исследуем поведение функции в окрестности точки
- 9. Родился в Париже в богатой и знатной
- 10. Неопределенность вида ТЕОРЕМА 1. Пусть
- 11. Доказательство. Пусть х∈ (a, b). Доопределим функции
- 12. ТЕОРЕМА 2. Пусть функции f(x) и g(x)
- 13. Доказательство. Можно считать, что a > 0. Положим
- 14. Неопределенность вида ТЕОРЕМА 3. Пусть
- 15. ЗАМЕЧАНИЕ 2. Правило Лопиталя справедливо также в
- 16. Примеры.1.2.3.4.
- 17. 5. Найдем Пусть k = [α]+1. Тогда
- 18. Спасибо за внимание!misis.ru
- 19. Скачать презентанцию
Слайды и текст этой презентации
Слайд 1Лекция 3.6
Приложения формулы Тейлора к вычислению пределов, выделению главной части
функции и исследованию поведения функции в окрестности точки.
неопределенностей.Слайд 2Вычисление пределов с помощью формулы Тейлора.
Рассмотрим
сначала случай неопределенности вида
Пусть требуется найти предел
где
Разложим по формуле Тейлора
функции f(x) и g(x) в окрестности точки x0, ограничившись лишь первыми не равными нулю членами, то есть f(x) = a(x – x0)n + o((x – x0)n), a ≠ 0,
g(x) = b(x – x0)m + o((x – x0)m), b ≠ 0.
Тогда
Слайд 3 Часто бывает удобно для разложений функций f(x) и g(x) использовать
готовый набор разложений элементарных функций по формуле Маклорена. Для этого
в случае, когда x0 ≠ 0, следует предварительно сделать замену переменной, положив t = x – x0. Тогда t → 0 при x → x0.ПРИМЕР 1.
Слайд 5 При раскрытии данным методом неопределенностей вида ∞/∞, 0·∞ и
∞ – ∞ их следует преобразовать к неопределенности вида 0/0.
Для
раскрытия неопределенностей вида 00, ∞0, 1∞ необходимо предварительно прологарифмировать рассматриваемые функции.ПРИМЕР 3.
Слайд 6Приложения формулы Тейлора к исследованию поведения функции в окрестности точки.
В
качестве примера применения формулы Тейлора для исследования поведения функции в
окрестности точки приведем доказательство третьего достаточного условия экстремума, использующего производные высших порядков.ТЕОРЕМА.
Пусть существует f (n)(x0), где n > 2, и выполняются условия:
f ´(x0) = f ´´(x0) = … = f (n-1) (x0) = 0, f (n) (x0) ≠ 0.
Тогда
Если n = 2k, то х0 – точка локального экстремума функции, а именно:
f (n) (x0) < 0 – точка строгого локального максимума.
f (n) (x0) > 0 – точка строгого локального минимума;
Если n = 2k+1, то x0 – не является точкой экстремума функции.
Слайд 7Доказательство.
Формула Тейлора n-ого порядка для функции f(x) в данном
случае имеет вид:
f(x) = f(x0) + f (n)( x0)(x –
x0)n/n! + о((x – x0)n).Отсюда получим
f(x) – f(x0) = f (n)( x0) /n! (1+ о(1)) (x – x0)n.
Если n = 2k, то (x – x0)n > 0 и разность f(x) – f(x0) имеет знак производной, то есть
f(x) < f(x0), если f (n) (x0) < 0, и х0 – точка локального максимума,
f(x) > f(x0), если f (n) (x0) > 0, и х0 – точка локального минимума.
Если n = 2k + 1, то (x – x0)n имеет разные знаки в левой и правой полуокрестности точки x0, то есть разность f(x) – f(x0) меняет знак при переходе через точку x0. Это означает, что эта точка не является точкой экстремума.
Слайд 8 ПРИМЕР.
Исследуем поведение функции
в окрестности точки x0 = 0.
Согласно
третьему достаточному условию экстремума, точка x0 = 0 является точкой
локального минимума функции. Значение функции в этой точке f(0) = 2.Разложение функции по формуле Маклорена имеет вид:
Слайд 9 Родился в Париже в богатой и знатной семье. Носил звание
маркиза (де Сен-Мэм) и графа (Антрмон). Служил капитаном кавалерии. Оставив
военную службу из-за близорукости, посвятил себя математике. Ученик Иоганна Бернулли.В 1693г. Лопиталя избрали членом Парижской академии наук. В 1696г. вышло из печати главное творение его жизни – «Анализ бесконечно малых для познания кривых линий». Это был первый печатный учебник по дифференциальному исчислению.
Скончался от апоплексического удара 43 лет от роду.
Правило Лопиталя раскрытия неопределенностей.
Гиймон Франсуа Лопиталь
(1661-1704 )
Слайд 10
Неопределенность вида
ТЕОРЕМА 1.
Пусть функции f(x) и g(x) дифференцируемы
на интервале (a, b),
g'(x) ≠ 0 для всех х∈
(a, b)и существует (где А – число или бесконечность)
Тогда существует
a
b
x
y
0
f(x)
g(x)
Слайд 11 Доказательство.
Пусть х∈ (a, b). Доопределим функции f(x) и g(x)
в точке а, положив f(а) = g(а) = 0. Тогда
доопределенные таким образом функции непрерывны на отрезке [а, х] и для них выполнены условия теоремы Коши, то естьЕсли х → а + 0, то ξ→ а + 0 и, по условию теоремы, существует
Поэтому существует и
x
a
ξ
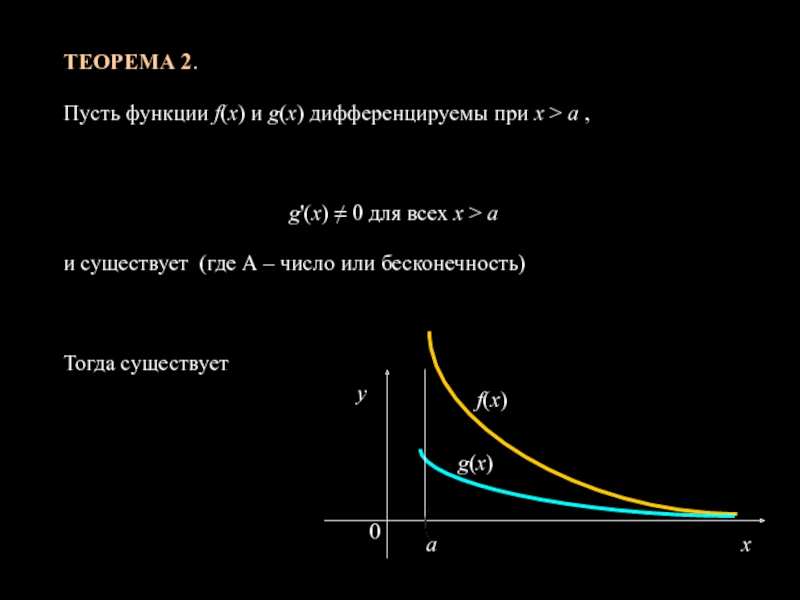
Слайд 12 ТЕОРЕМА 2.
Пусть функции f(x) и g(x) дифференцируемы при х
> а ,
g'(x) ≠ 0 для всех х >
а и существует (где А – число или бесконечность)
Тогда существует
a
x
y
0
f(x)
g(x)
Слайд 13 Доказательство.
Можно считать, что a > 0. Положим x = 1/t.
Эта функция отображает интервал (а, +∞) на интервал (0, 1/а).
ЗАМЕЧАНИЕ
1. Правило Лопиталя справедливо также в случае неопределенности
при х → а – 0,
при х → а,
при х → – ∞,
при х → ∞
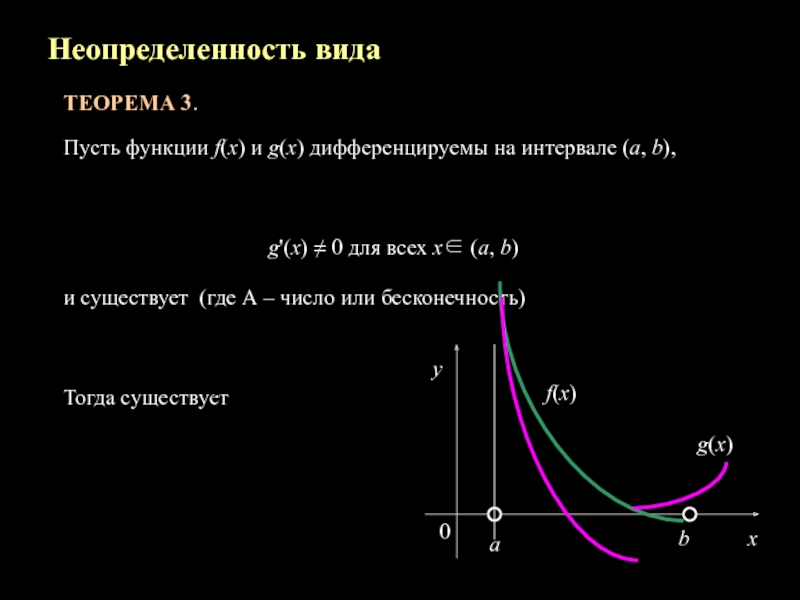
Слайд 14
Неопределенность вида
ТЕОРЕМА 3.
Пусть функции f(x) и g(x) дифференцируемы
на интервале (a, b),
g'(x) ≠ 0 для всех х∈
(a, b)и существует (где А – число или бесконечность)
Тогда существует
a
b
x
y
0
f(x)
g(x)
Слайд 15 ЗАМЕЧАНИЕ 2.
Правило Лопиталя справедливо также в случае неопределенности
при х
→ а – 0,
при х → а,
при х →
– ∞, при х → + ∞,
при х → ∞.
ЗАМЕЧАНИЕ 3.
Чтобы применить правило Лопиталя для раскрытия неопределенностей вида 0·∞ и ∞ – ∞, их следует привести к виду 0/0 или ∞/∞.
Неопределенности вида 00, ∞0, 1∞ можно раскрыть, предварительно прологарифмировав соответствующие функции.
Слайд 175. Найдем
Пусть k = [α]+1. Тогда α – k
< 0. Применяя правило Лопиталя k раз, получаем
6. Найдем
Пусть lnx = t. Тогда
7. Покажем, что
не может быть найден по правилу Лопиталя.
Заметим, что
т.е. предел существует.
Однако
не существует, так как, взяв две ЧП
получим













![Приложения формулы Тейлора к вычислению пределов 5. Найдем Пусть k = [α]+1. Тогда α – k < 5. Найдем Пусть k = [α]+1. Тогда α – k < 0. Применяя правило Лопиталя k раз,](/img/thumbs/62665435eb8b7b81c3b5d39935ea0b38-800x.jpg)