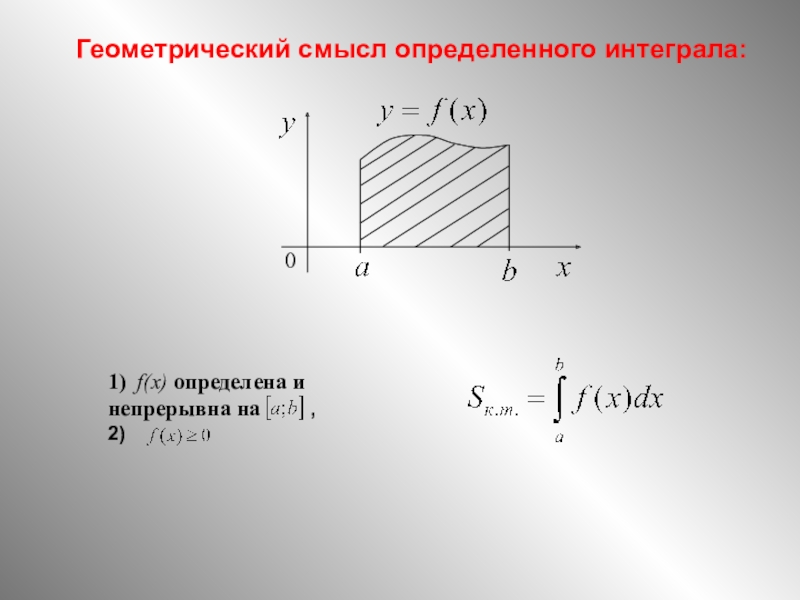
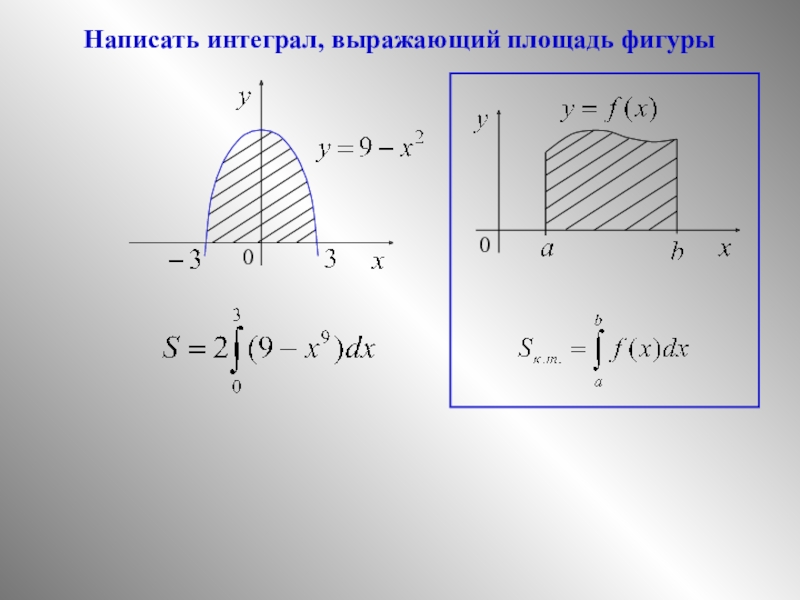
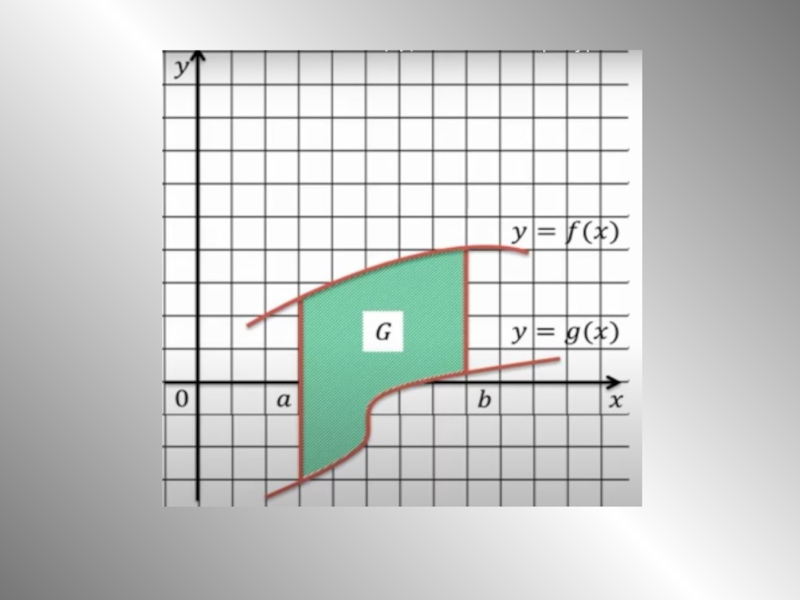
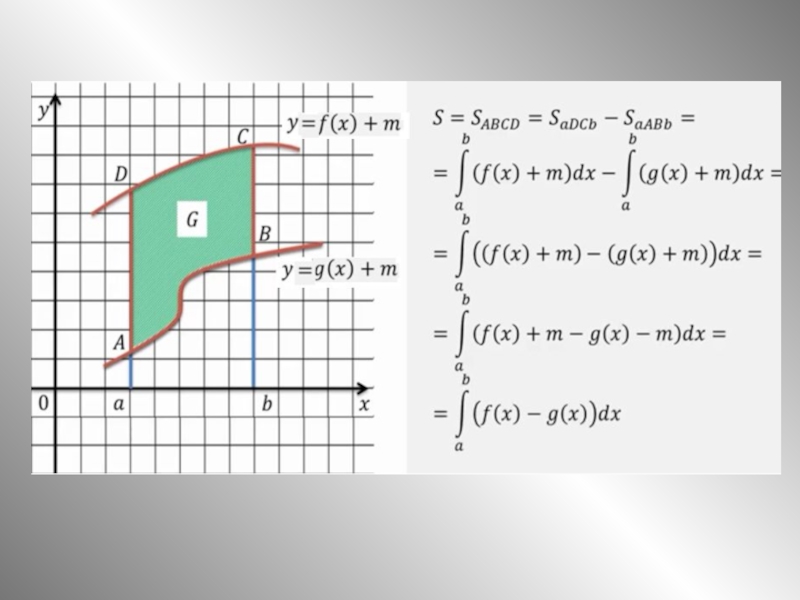
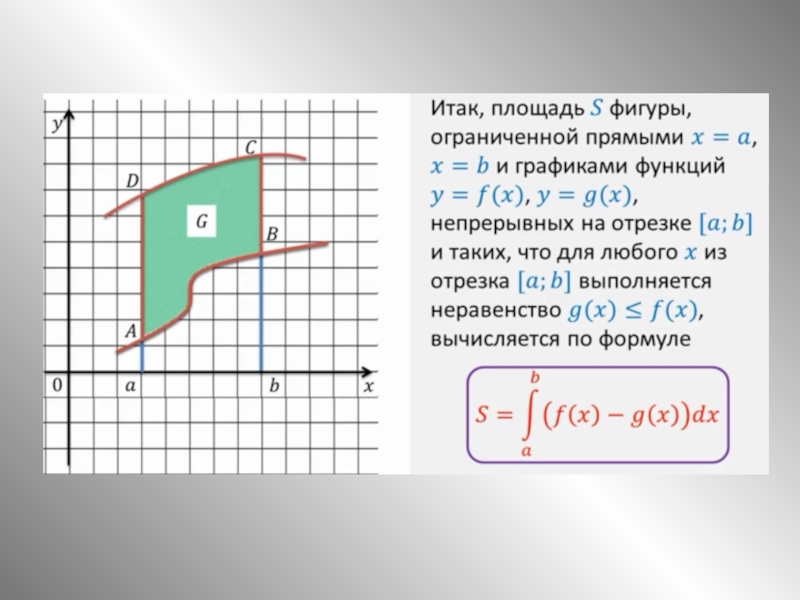
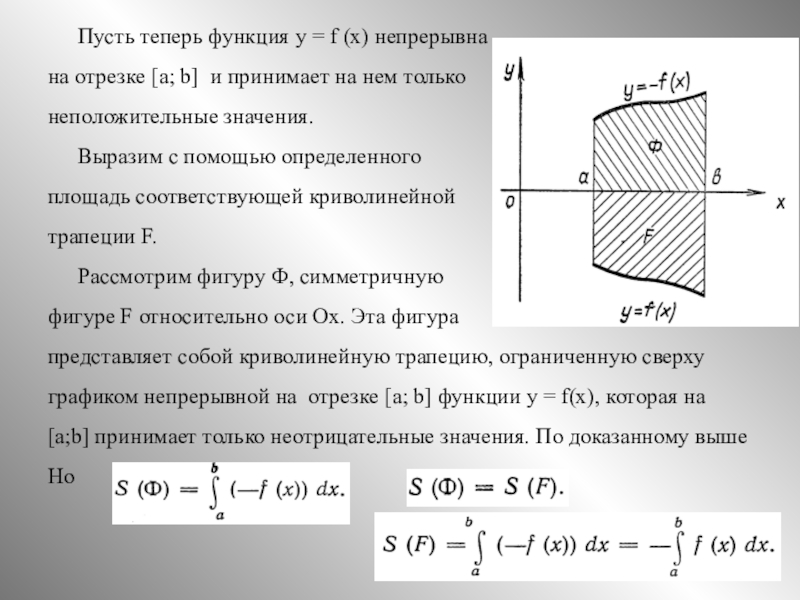
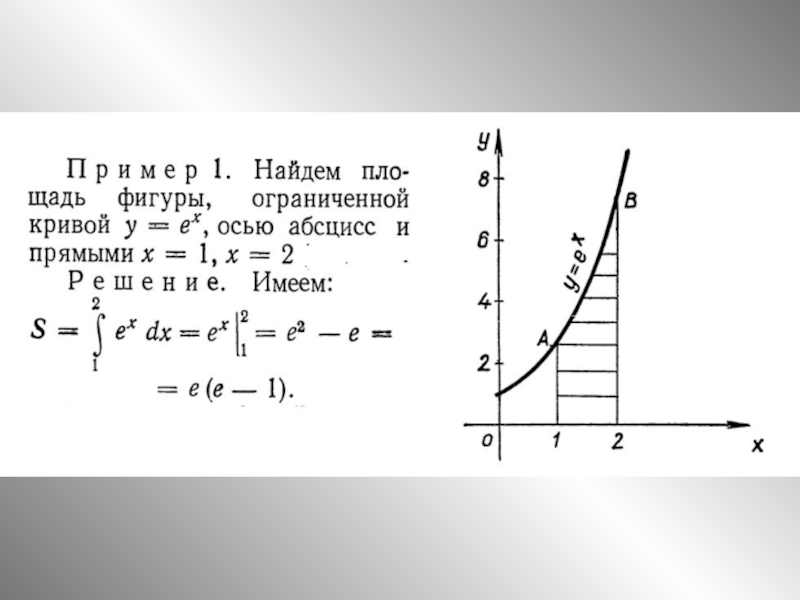
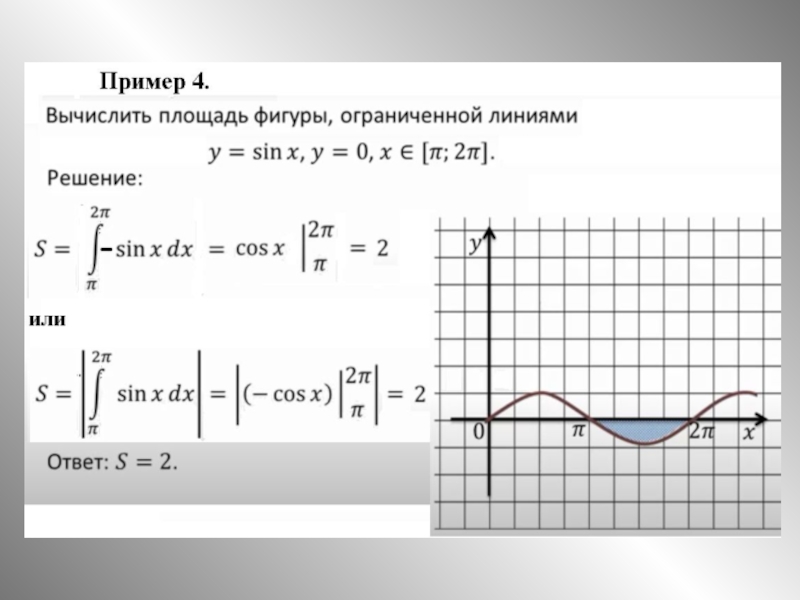
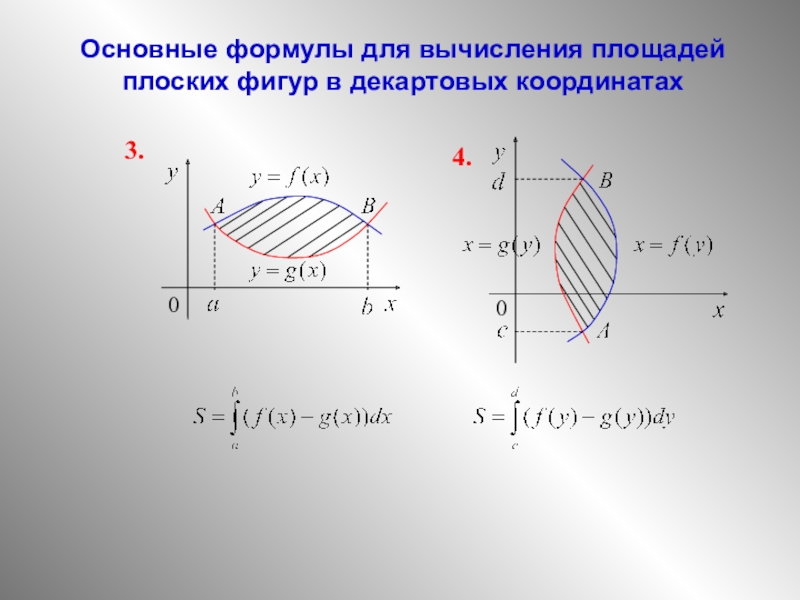
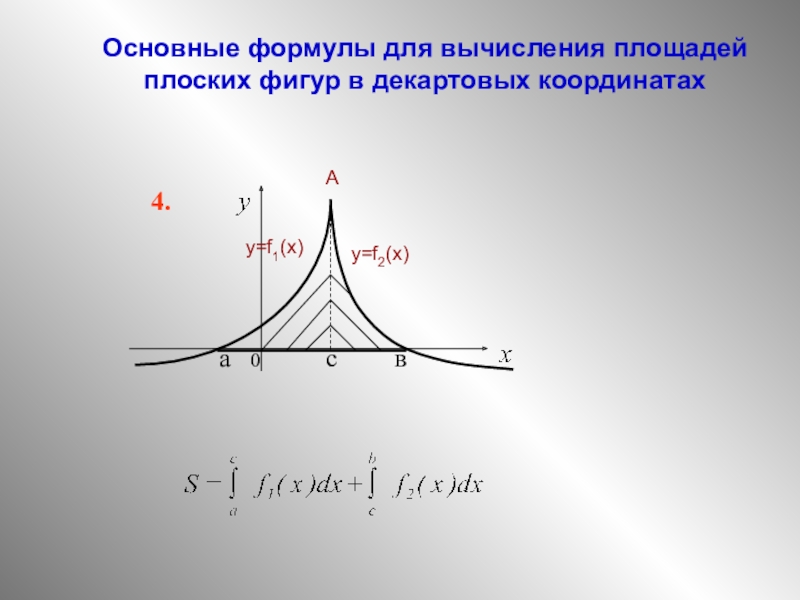
на отрезке [а; b] и принимает на нем только неположительные значения.
Выразим с помощью определенного интеграла площадь соответствующей криволинейной трапеции F.
Рассмотрим фигуру Ф, симметричную фигуре F относительно оси Ох. Эта фигура представляет собой криволинейную трапецию, ограниченную сверху графиком непрерывной на отрезке [а; b] функции у = f(х), которая на [а;b] принимает только неотрицательные значения. По доказанному выше Но Значит,