Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Применение поиска в глубину. Нахождение в графе компонент двусвязности
Содержание
- 1. Применение поиска в глубину. Нахождение в графе компонент двусвязности
- 2. 21.04.2014Двусязные компонентыНахождение компонент двусвязности графа (biconnected components)НапоминаниеГраф
- 3. 21.04.2014Двусязные компонентыТочки сочленения и двусвязные компонентыПусть G
- 4. 21.04.2014Двусязные компонентыРавнозначное утверждение:Точка сочленения – такая вершина
- 5. 21.04.2014Двусязные компоненты Граф G – двусвязный (неразделимый), если
- 6. 21.04.2014Двусязные компонентыТривиальный алгоритм: перебираем все вершины -
- 7. 21.04.2014Двусязные компонентыВ основе – Свойство DFS-остова
- 8. 21.04.2014Двусязные компонентыИллюстрация к доказательству: {u,v} ∈ E
- 9. ЗамечаниеПо схеме A⇒B, not B ⇒ not
- 10. 21.04.2014Двусязные компонентыТеорема: Пусть D = (V, T)
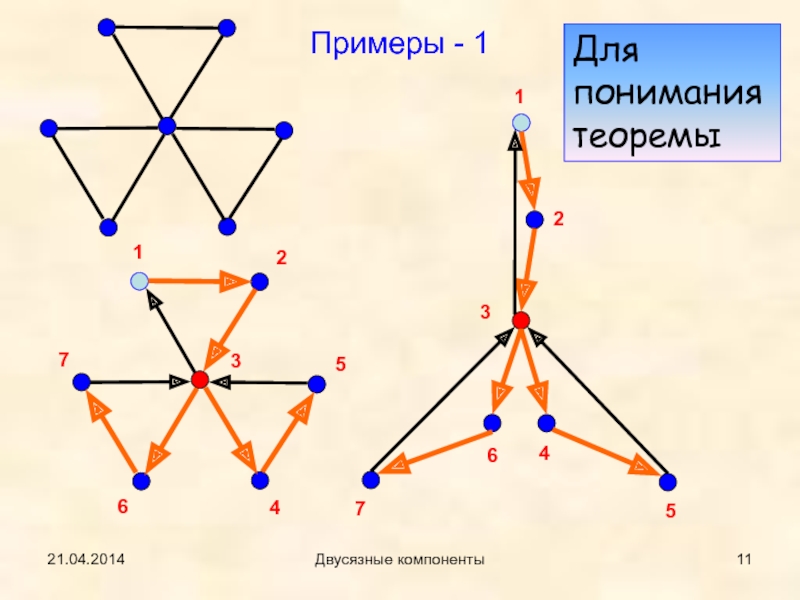
- 11. 21.04.2014Двусязные компонентыПримеры - 11234567Для понимания теоремы
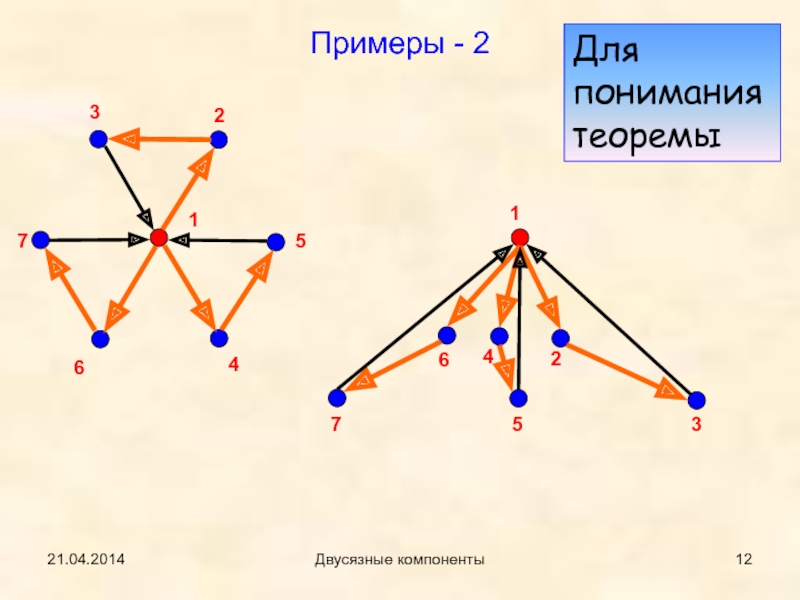
- 12. 21.04.2014Двусязные компонентыПримеры - 212345671234567Для понимания теоремы
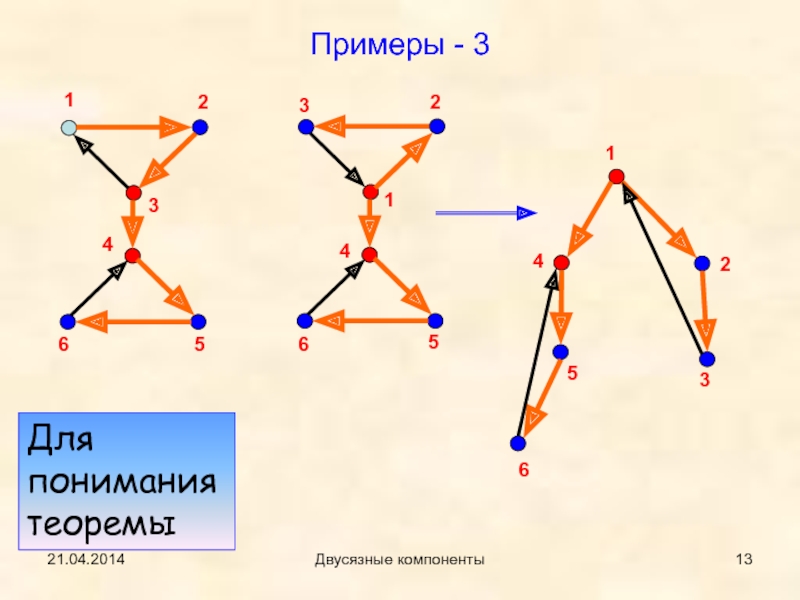
- 13. 21.04.2014Двусязные компонентыПримеры - 3123456123456123456Для понимания теоремы
- 14. 21.04.2014Двусязные компонентыДоказательство: 2) a ≠ r и
- 15. 21.04.2014Двусязные компоненты… либо есть обратное ребро. Покажем,
- 16. 21.04.2014Двусязные компонентыТогда опять либо нет обратного ребра
- 17. Следующая идеяЭтой теореме нужно придать такую форму,
- 18. 21.04.2014Двусязные компонентыДля каждой вершины v∈V определим множество
- 19. 21.04.2014Двусязные компонентыLow(s) ≥ NumVert(a) Иными словами -
- 20. 21.04.2014Двусязные компонентыОпять тот же «Пример 1»12345671113333Low(s)Low(6) = NumVert(3) Low(4) = NumVert(3) Low(s) ≥ NumVert(a) 33
- 21. 21.04.2014Двусязные компонентыНахождение компонент двусвязности графа (BiConnection) (на
- 22. 21.04.2014Двусязные компонентыТело процедуры BICON iV++; //посетить
- 23. 21.04.2014Двусязные компоненты if (NumVert[w]==0) {// -
- 24. 21.04.2014Двусязные компоненты else // w -
- 25. 21.04.2014Двусязные компоненты{ …SetVert V; //множество вершин графа
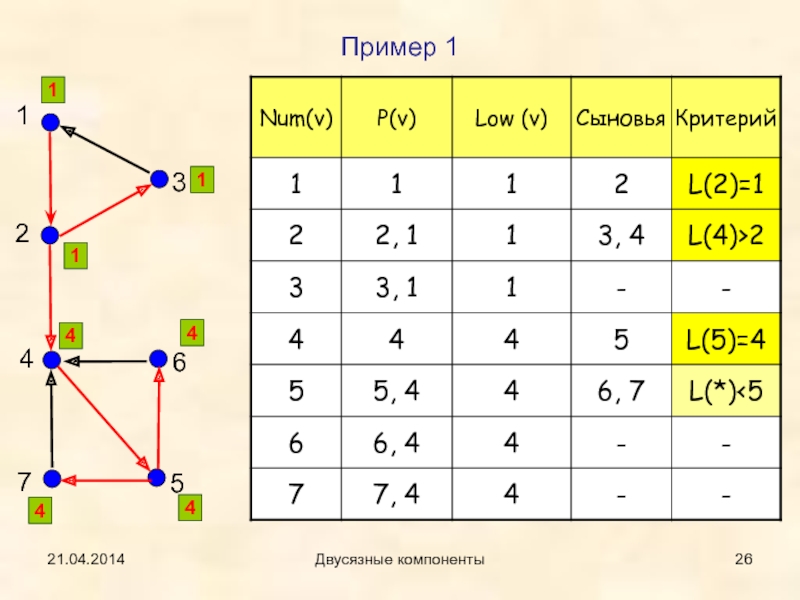
- 26. 21.04.2014Двусязные компонентыПример 11114444
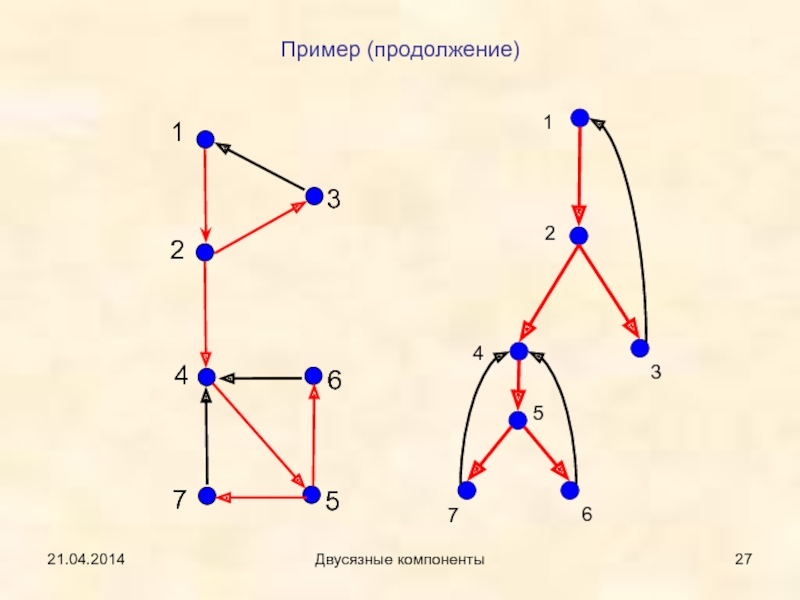
- 27. 21.04.2014Двусязные компонентыПример (продолжение)1234567
- 28. 21.04.2014Двусязные компонентыПроцесс обходаL(1) = 1L(2) = 1L(3)
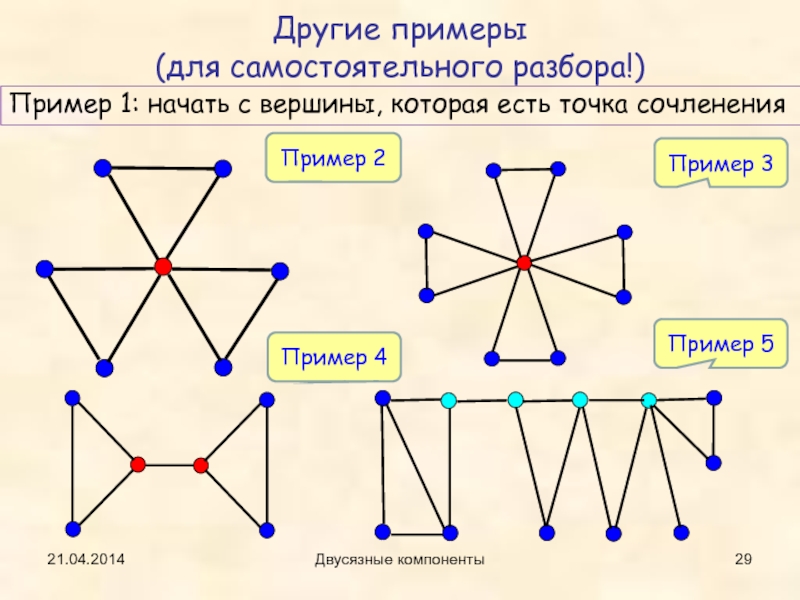
- 29. 21.04.2014Двусязные компонентыПример 1: начать с вершины, которая
- 30. 21.04.2014Двусязные компонентыПродолжение лекции в следующей презентации: Поиск в глубину в орграфе Топологическая сортировка
- 31. 21.04.2014Двусязные компонентыКОНЕЦ ЛЕКЦИИКОНЕЦ ЛЕКЦИИКОНЕЦ
- 32. Скачать презентанцию
Слайды и текст этой презентации
Слайд 121.04.2014
Двусязные компоненты
Построение и анализ алгоритмов
Лекция 10.1
Раздел: Алгоритмы на графах
Тема лекции:
Слайд 221.04.2014
Двусязные компоненты
Нахождение компонент двусвязности графа
(biconnected components)
Напоминание
Граф называется связным, если любая
пара вершин в графе соединена путем.
Связная компонента графа – максимальный
связный подграф.Максимальный подграф – по включению (не входит ни в какой другой связный подграф).
Слайд 321.04.2014
Двусязные компоненты
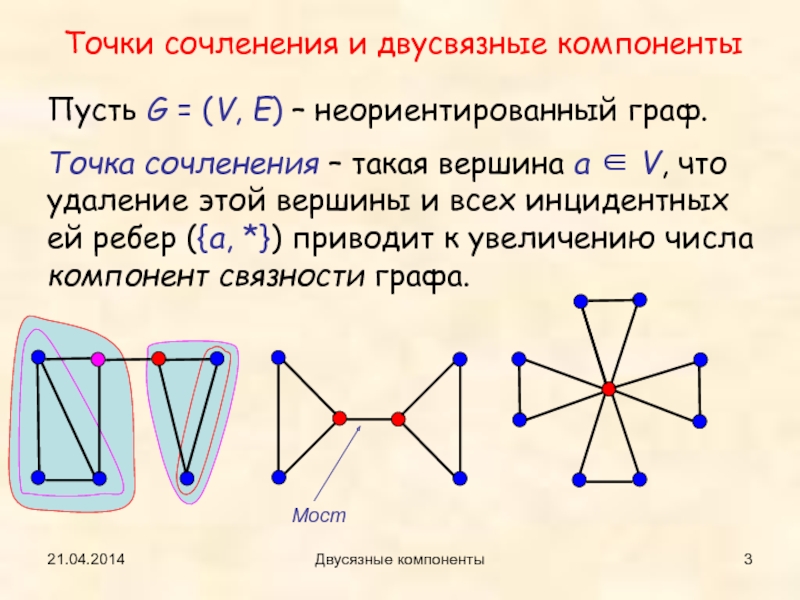
Точки сочленения и двусвязные компоненты
Пусть G = (V, E)
– неориентированный граф.
Точка сочленения – такая вершина a ∈ V,
что удаление этой вершины и всех инцидентных ей ребер ({a, *}) приводит к увеличению числа компонент связности графа.Мост
Слайд 421.04.2014
Двусязные компоненты
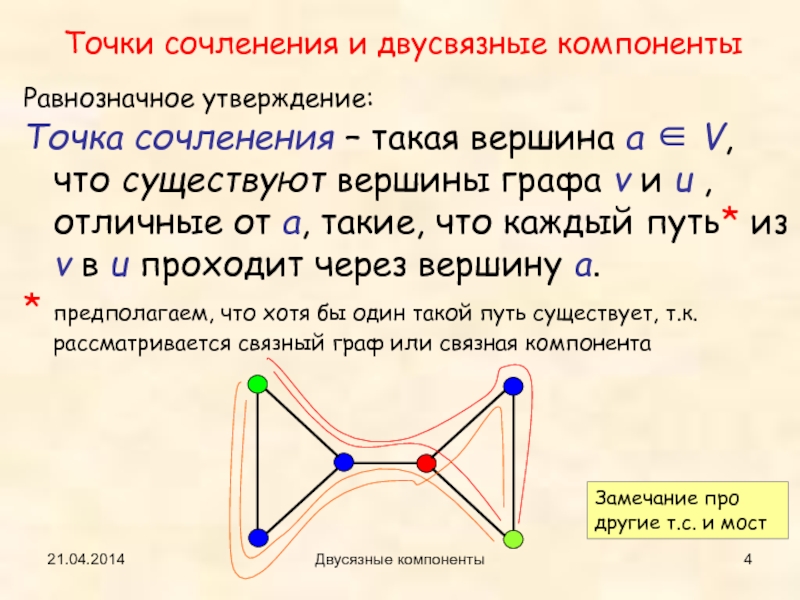
Равнозначное утверждение:
Точка сочленения – такая вершина a ∈ V,
что существуют вершины графа v и u , отличные от
a, такие, что каждый путь* из v в u проходит через вершину a.* предполагаем, что хотя бы один такой путь существует, т.к. рассматривается связный граф или связная компонента
Точки сочленения и двусвязные компоненты
Замечание про другие т.с. и мост
Слайд 521.04.2014
Двусязные компоненты
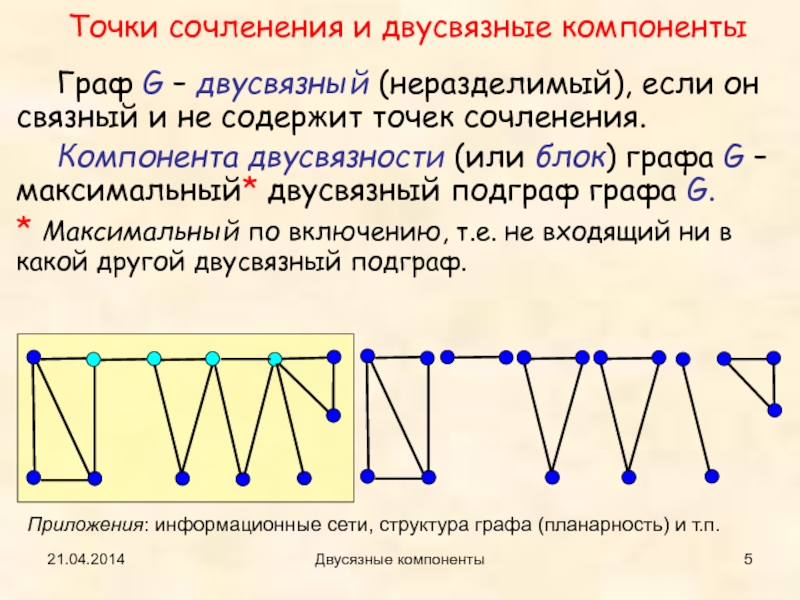
Граф G – двусвязный (неразделимый), если он связный и
не содержит точек сочленения.
Компонента двусвязности (или блок) графа G –
максимальный* двусвязный подграф графа G.* Максимальный по включению, т.е. не входящий ни в какой другой двусвязный подграф.
Точки сочленения и двусвязные компоненты
Приложения: информационные сети, структура графа (планарность) и т.п.
Слайд 621.04.2014
Двусязные компоненты
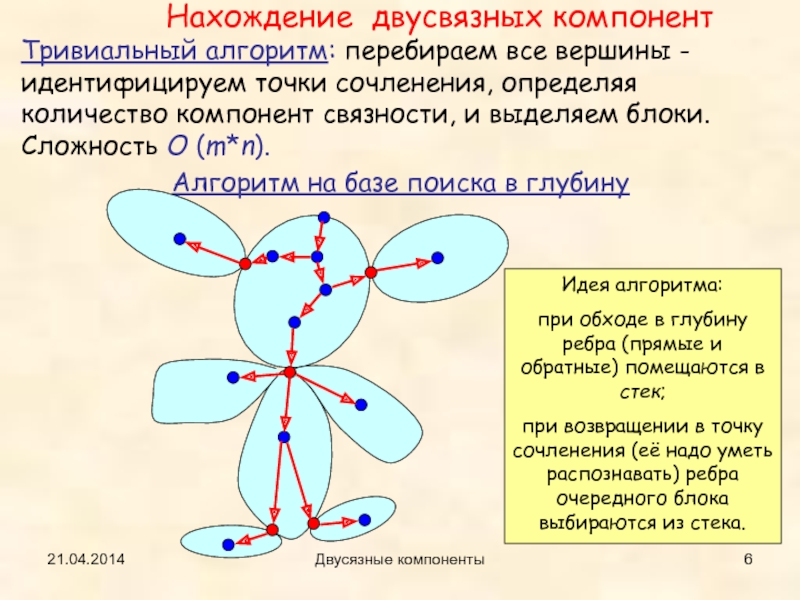
Тривиальный алгоритм: перебираем все вершины - идентифицируем точки сочленения,
определяя количество компонент связности, и выделяем блоки. Сложность O (m*n).
Алгоритм
на базе поиска в глубинуНахождение двусвязных компонент
Идея алгоритма:
при обходе в глубину ребра (прямые и обратные) помещаются в стек;
при возвращении в точку сочленения (её надо уметь распознавать) ребра очередного блока выбираются из стека.
Слайд 721.04.2014
Двусязные компоненты
В основе –
Свойство DFS-остова (глубинного остовного дерева) [см.лекцию
8.1, сл.25-26]
Пусть (V, T) – DFS-остов графа G = (V,
E) и пусть {u, v}∈E. Тогда либо u потомок v (в дереве), либо v потомок u.Доказательство.
Пусть v посещена раньше, чем u. По завершении TDFS(v), будет NumVert[v] < NumVert[u], т.к. {u,v} ∈ E. Но это значит, что в TDFS добавились ребра, содержащие путь из v в u. Отсюда следует, что v лежит на пути от корня в u, т.е. u потомок v.
Аналогично рассуждаем в случае, если u посещена раньше, чем v.
Слайд 821.04.2014
Двусязные компоненты
Иллюстрация к доказательству:
{u,v} ∈ E
v посещена раньше,
чем u
numVert[v] < numVert[u]
r – корень TDFS
v
u
r
Свойство TDFS-остова
(глубинного остовного дерева) Слайд 9Замечание
По схеме A⇒B, not B ⇒ not A.
21.04.2014
Двусязные компоненты
Пусть (V,
T) – DFS-остов графа G = (V, E) и пусть
{u, v} ∈ E. Тогда либо u потомок v (в дереве), либо v потомок u.Т.е. ({u, v} ∈ E) ⇒ (либо u потомок v (в дереве), либо v потомок u)
(т.е. u и v связаны отношением «предок-потомок» в дереве)
not (u и v связаны отношением «предок-потомок» в дереве) ⇒ not ({u, v} ∈ E)
Слайд 1021.04.2014
Двусязные компоненты
Теорема: Пусть D = (V, T) – глубинное остовное
дерево связного графа G = (V, E) с корнем дерева
r.Вершина a ∈V является точкой сочленения графа G ттогда, когда выполнено одно из условий:
a = r и a имеет более одного сына в D (хотя бы двух);
a ≠ r и существует s = сын (a) , такой что НЕТ обратных ребер, идущих от потомков вершины s (в том числе самой s) к предкам вершины a.
Нахождение двусвязных компонент
Доказательство: 1) a = r
1а) a имеет только одного сына …
1б) a имеет хотя бы двух сыновей…
Слайд 1421.04.2014
Двусязные компоненты
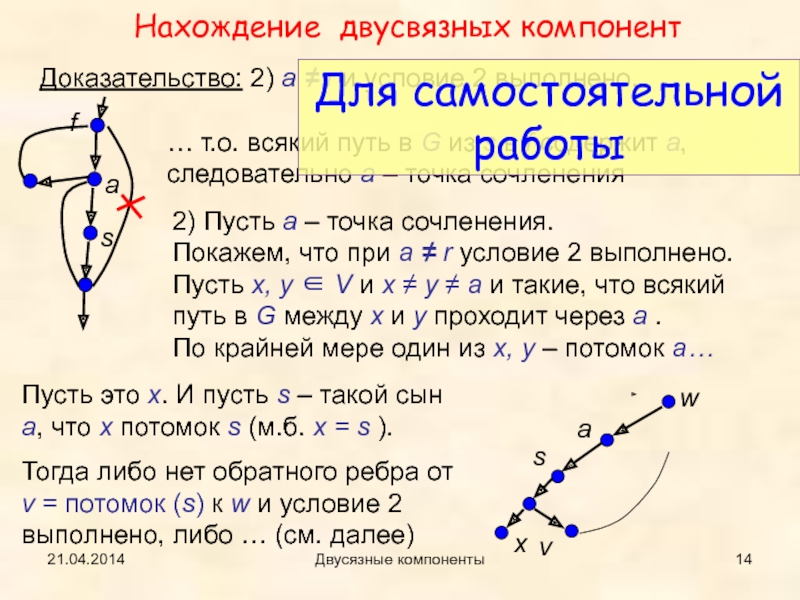
Доказательство: 2) a ≠ r и условие 2 выполнено.
Нахождение
двусвязных компонент
s
f
a
… т.о. всякий путь в G из s в
f содержит a, следовательно a – точка сочленения 2) Пусть a – точка сочленения.
Покажем, что при a ≠ r условие 2 выполнено.
Пусть x, y ∈ V и x ≠ y ≠ a и такие, что всякий путь в G между x и y проходит через a .
По крайней мере один из x, y – потомок a…
Пусть это x. И пусть s – такой сын a, что x потомок s (м.б. x = s ).
Тогда либо нет обратного ребра от v = потомок (s) к w и условие 2 выполнено, либо … (см. далее)
Для самостоятельной работы
Слайд 1521.04.2014
Двусязные компоненты
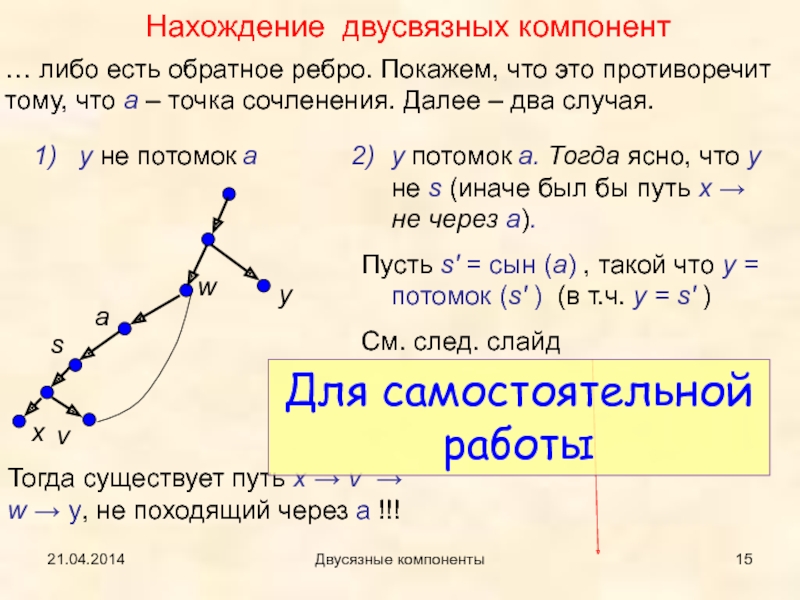
… либо есть обратное ребро. Покажем, что это противоречит
тому, что a – точка сочленения. Далее – два случая.
Нахождение
двусвязных компонент1) y не потомок a
Тогда существует путь x → v → w → y, не походящий через a !!!
y потомок a. Тогда ясно, что y не s (иначе был бы путь x → не через a).
Пусть s′ = сын (a) , такой что y = потомок (s′ ) (в т.ч. y = s′ )
См. след. слайд
Для самостоятельной работы
Слайд 1621.04.2014
Двусязные компоненты
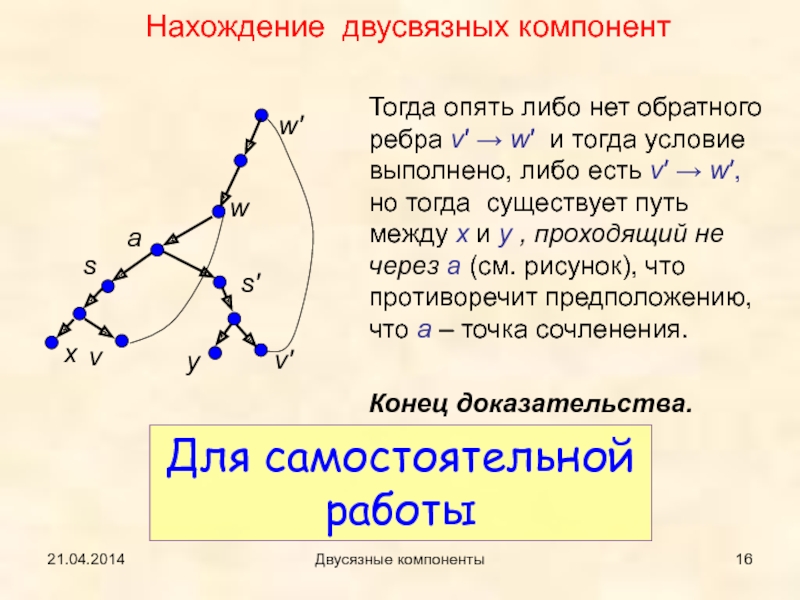
Тогда опять либо нет обратного ребра v′ → w′
и тогда условие выполнено, либо есть v′ → w′, но
тогда существует путь между x и y , проходящий не через a (см. рисунок), что противоречит предположению, что a – точка сочленения.Конец доказательства.
a
s
w
v
x
y
Нахождение двусвязных компонент
v′
s′
w′
Для самостоятельной работы
Слайд 17Следующая идея
Этой теореме нужно придать такую форму,
в которой она
может быть использована
как критерий для нахождения точек сочленения при
поиске в глубину21.04.2014
Двусязные компоненты
Слайд 1821.04.2014
Двусязные компоненты
Для каждой вершины v∈V определим множество P(v)
P(v) = {v}
U { w : (w = предок(v)) &
(∃ x∈V:
((x = v) ∨ (x=потомок(v ))) & (где B - множество обратных ребер (хорд).
Иными словами P (v) состоит из v и всех предков v, которых можно достичь из v , проходя сначала несколько (возможно, ни одной) дуг дерева T, а затем одно обратное ребро.
Введем функцию Low(v) = Min { NumVert(x) ⎢ x ∈ P (v) }.
Нахождение двусвязных компонент
Утверждение (эквивалентное теореме):
Вершина a ≠ r является точкой сочленения графа G ттогда, когда существует s = сын (a) , такой что
Low(s) ≥ NumVert(a)
Слайд 1921.04.2014
Двусязные компоненты
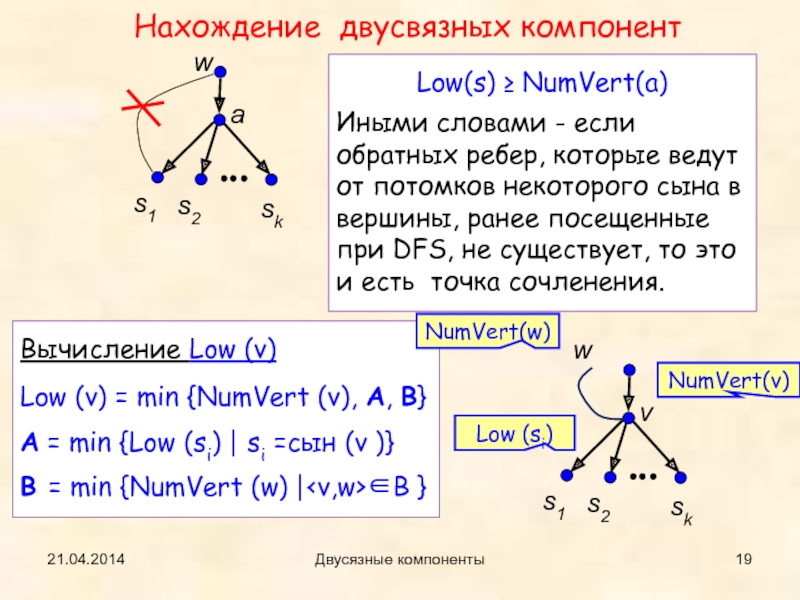
Low(s) ≥ NumVert(a)
Иными словами - если обратных ребер,
которые ведут от потомков некоторого сына в вершины, ранее посещенные
при DFS, не существует, то это и есть точка сочленения.Нахождение двусвязных компонент
w
Вычисление Low (v) w Low (si) NumVert(v) NumVert(w)
Low (v) = min {NumVert (v), A, B}
A = min {Low (si) ⎢ si =сын (v )}
B = min {NumVert (w) ⎢
Слайд 2021.04.2014
Двусязные компоненты
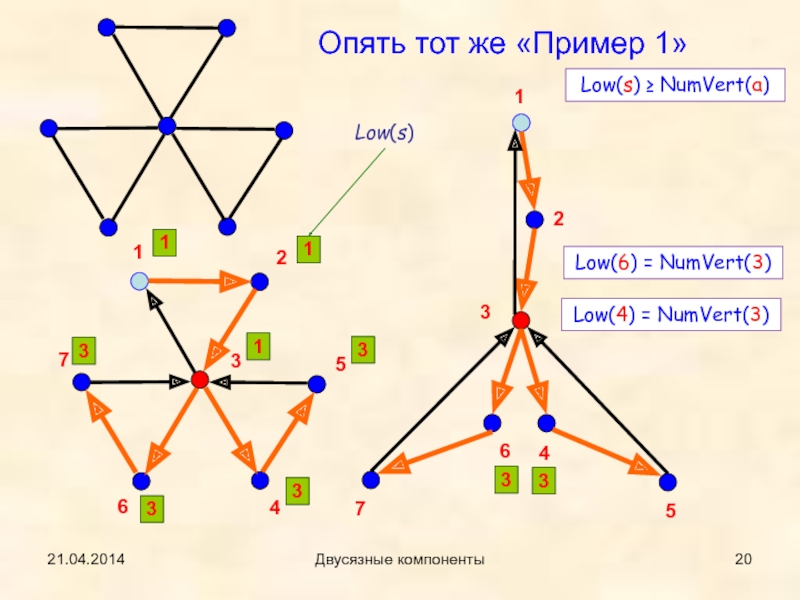
Опять тот же «Пример 1»
1
2
3
4
5
6
7
1
1
1
3
3
3
3
Low(s)
Low(6) = NumVert(3)
Low(4) =
NumVert(3)
Low(s) ≥ NumVert(a)
3
3
Слайд 2121.04.2014
Двусязные компоненты
Нахождение компонент двусвязности графа (BiConnection)
(на основе поиска в глубину)
BICON
(vert v, vert u)
{ // посещаем вершину v и т.д.;
u=Отец(v)global int numVert [n];
listVert Adj [n] ; // списки смежности
int iV; /*текущий порядковый номер посещения вершины*/
int Low [n] ;
stack
Слайд 2221.04.2014
Двусязные компоненты
Тело процедуры BICON
iV++;
//посетить v:
numVert[v]
= iV;
Low[v] = numVert[v];
for (∀ w ∈ Adj[v] )
if (NumVert[w]==0) {
//
…
Слайд 2321.04.2014
Двусязные компоненты
if (NumVert[w]==0) {// - ребро (ветвь) остовного
дерева
st ← {v,w};
BICON ( w, v);Low[v] := min (Low[v],Low[w]); //здесь Low[w] окончательное
if (Low[w] >= NumVert[v] ) {
/* v - либо корень, либо точка сочленения, а в стеке
сверху до
двувязности; выписать (зафиксировать) их */
do {
e ← st;
cout << e;
} while (e == {v,w});
cout << 'end of Block‘ << endl;
} //if
} //if-then
Продолжение (тело основного цикла)
Слайд 2421.04.2014
Двусязные компоненты
else // w - уже посещалась
if ((NumVert[w] < NumVert[v]) && (w!=u) )
{//
st ← {v,w};
Low[v] = min ( Low[v], numVert[w] );
}//if
//od for, v - использована
} //BICON
Продолжение (тело основного цикла)
Слайд 2521.04.2014
Двусязные компоненты
{ …
SetVert V; //множество вершин графа G=(V,E), Card(V)=n
int numVert
[n] ;
listVert adj[n]; //списки смежности
int iV; //текущий порядковый номер
посещения вершиныint Low[n];
stack
for (∀v∈V) numVert[v] = 0;
// - пометить все вершины как необследованные
iV = 0;
Empty(St);
for ( ∀v∈V)
if (numVert[v]==0) BICON (v, v);
}
Главная программа нахождения
компонент двусвязности графа G=(V,E)
Слайд 2821.04.2014
Двусязные компоненты
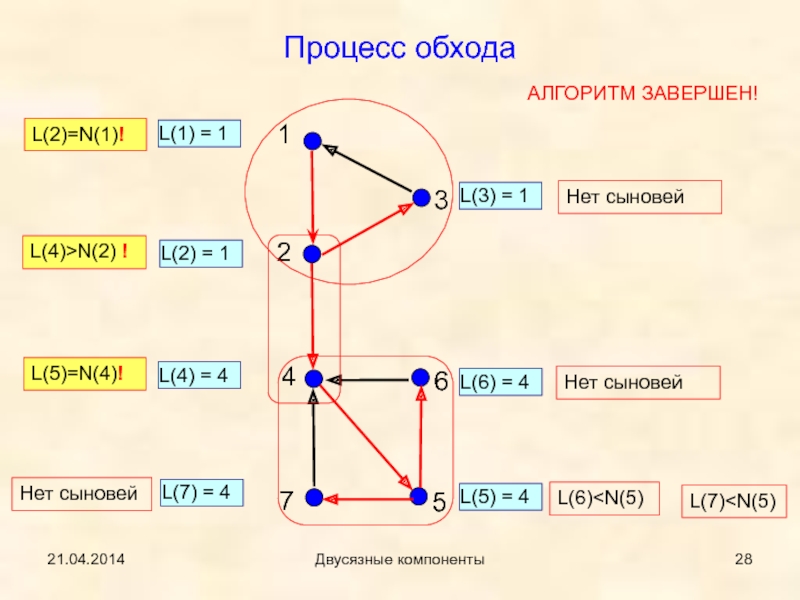
Процесс обхода
L(1) = 1
L(2) = 1
L(3) = 1
L(4) =
4
L(5) = 4
L(6) = 4
L(7) = 4
L(5)=N(4)!
Нет сыновей
L(6)N(2) !
L(2)=N(1)!
Нет
сыновейL(7) АЛГОРИТМ ЗАВЕРШЕН!


![Применение поиска в глубину. Нахождение в графе компонент двусвязности 21.04.2014Двусязные компонентыВ основе – Свойство DFS-остова (глубинного остовного дерева) [см.лекцию 8.1, 21.04.2014Двусязные компонентыВ основе – Свойство DFS-остова (глубинного остовного дерева) [см.лекцию 8.1, сл.25-26]Пусть (V, T) – DFS-остов](/img/thumbs/e43ca340059905d63e03dd73086c8fb6-800x.jpg)
![Применение поиска в глубину. Нахождение в графе компонент двусвязности 21.04.2014Двусязные компонентыИллюстрация к доказательству: {u,v} ∈ E v посещена раньше, чем 21.04.2014Двусязные компонентыИллюстрация к доказательству: {u,v} ∈ E v посещена раньше, чем u numVert[v] < numVert[u] r –](/img/thumbs/16a28953164ef3d2458a0910ff1d831f-800x.jpg)





![Применение поиска в глубину. Нахождение в графе компонент двусвязности 21.04.2014Двусязные компонентыТело процедуры BICON iV++; //посетить v: numVert[v] = iV; 21.04.2014Двусязные компонентыТело процедуры BICON iV++; //посетить v: numVert[v] = iV; Low[v] = numVert[v];](/img/thumbs/685a538c09f975bd9539f6f4eab1995d-800x.jpg)
![Применение поиска в глубину. Нахождение в графе компонент двусвязности 21.04.2014Двусязные компоненты if (NumVert[w]==0) {// - ребро (ветвь) остовного дерева 21.04.2014Двусязные компоненты if (NumVert[w]==0) {// - ребро (ветвь) остовного дерева st ←](/img/thumbs/0e2ed851d1b7b506006efaf24501a30e-800x.jpg)
![Применение поиска в глубину. Нахождение в графе компонент двусвязности 21.04.2014Двусязные компоненты else // w - уже посещалась 21.04.2014Двусязные компоненты else // w - уже посещалась if ((NumVert[w] < NumVert[v])](/img/thumbs/bc5d2328f3f77dbad020f9c5febab00d-800x.jpg)
![Применение поиска в глубину. Нахождение в графе компонент двусвязности 21.04.2014Двусязные компоненты{ …SetVert V; //множество вершин графа G=(V,E), Card(V)=nint numVert [n] 21.04.2014Двусязные компоненты{ …SetVert V; //множество вершин графа G=(V,E), Card(V)=nint numVert [n] ;listVert adj[n]; //списки смежности int iV;](/img/thumbs/64bb2c83e6b7b2a575663950b8986172-800x.jpg)