четной, нечетной, является ли периодической.
3. Найти точки пересечения графика с
осями координат.4. Промежутки знакопостоянства (промежутки, на которых f(x)>0 или f(x)<0).
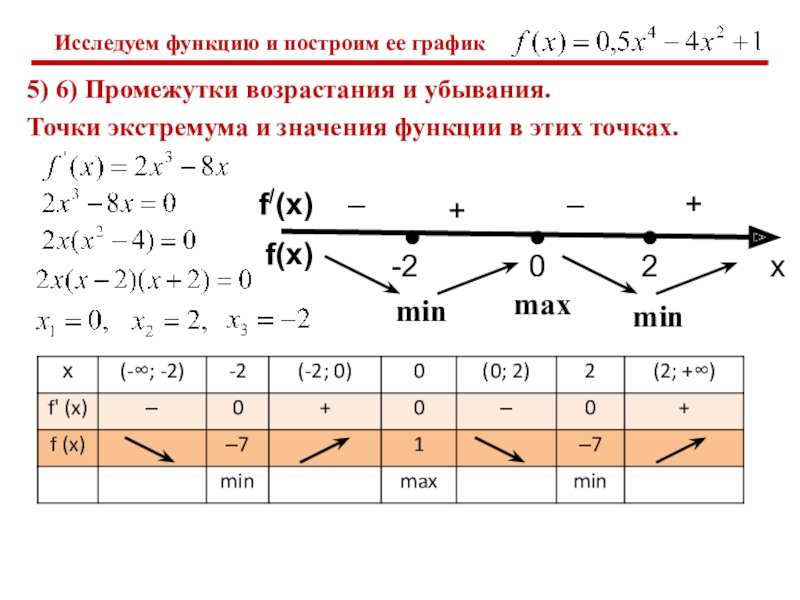
5. Промежутки возрастания и убывания.
6. Точки экстремума и значения функции в этих точках.
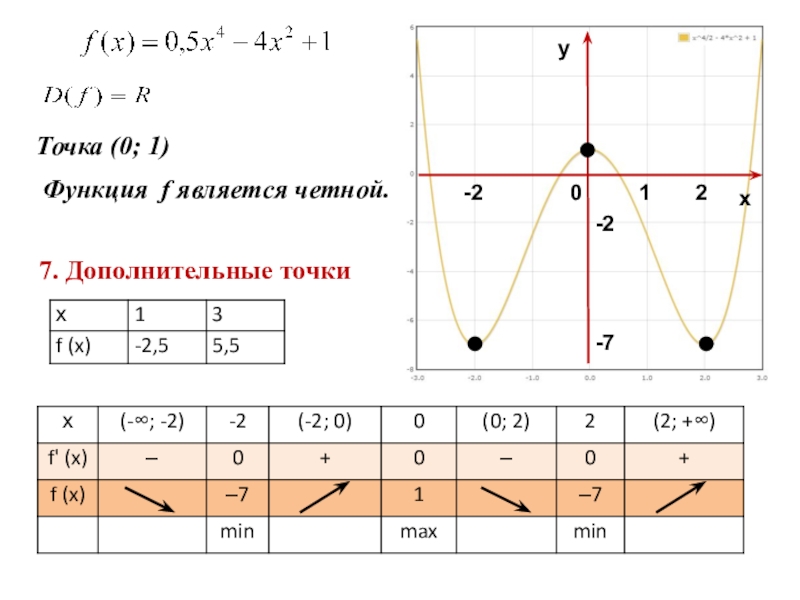
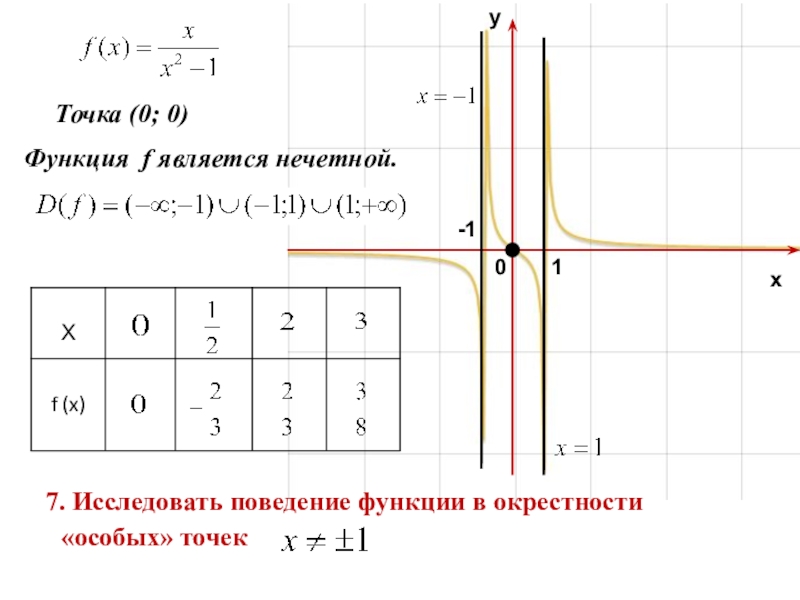
7. Исследовать поведение функции в окрестности «особых» точек и при больших по модулю х.