Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Принятие решений в условиях неопределенности
Содержание
- 1. Принятие решений в условиях неопределенности
- 2. Принятие решений в условиях неопределенности требует определения
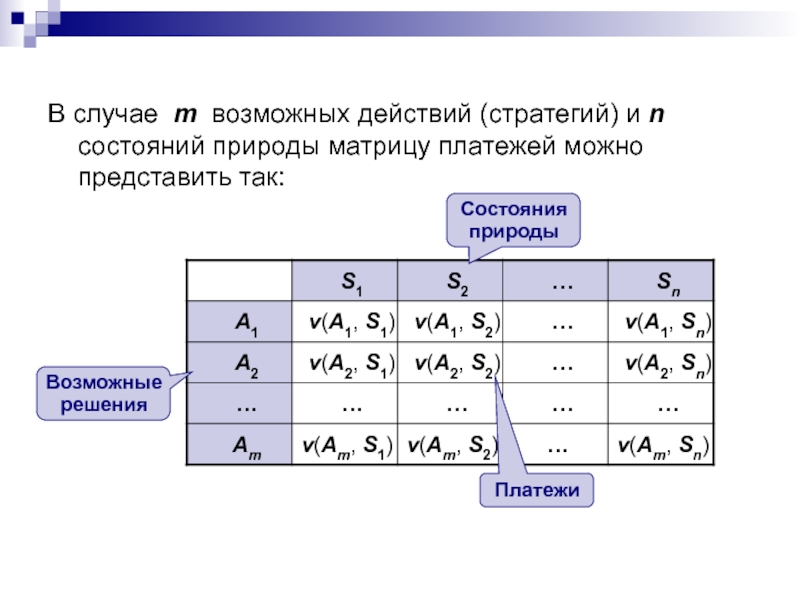
- 3. В случае m возможных действий (стратегий) и
- 4. Отличие принятия решений в условиях неопределенности от
- 5. Критерии для анализа ситуации, связанной с принятием
- 6. Критерий ЛапласаОпирается на принцип недостаточного основания: распределение вероятностей
- 7. Если при этом v(Аi, Sj) представляет получаемую
- 8. Максиминный (минимаксный) критерийОснован на консервативном осторожном поведении ЛПР и сводится к выбору наилучшей альтернативы из наихудших.
- 9. Еслиv(Аi, Sj) представляет получаемую прибыль, то наилучшим
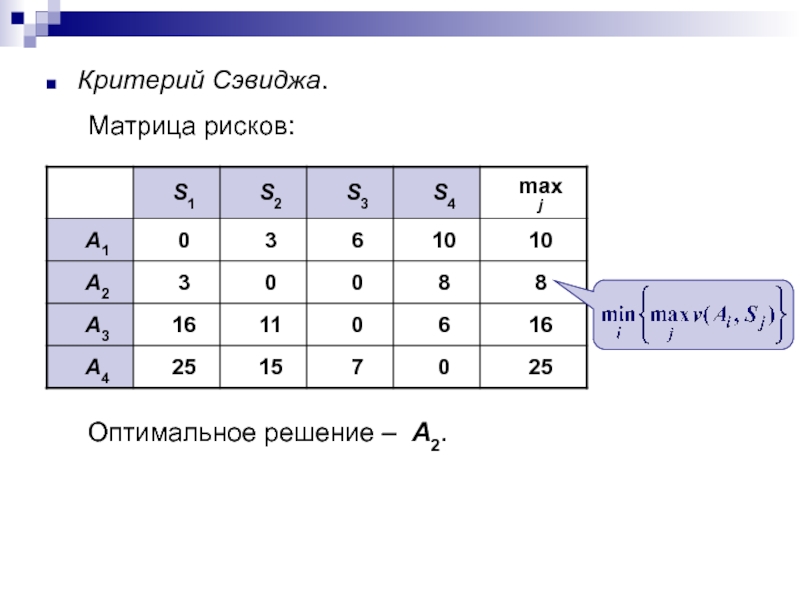
- 10. Критерий Сэвиджа Попытка смягчить консерватизм максиминного (минимаксного)
- 11. Пример. Матрица платежей (расходов): Согласно минимаксному критерию решение А2
- 12. Составим матрицу потерь (матрицу рисков): Согласно минимаксному критерию, примененному к матрице потерь, решение А1 является предпочтительным.
- 13. Критерий ГурвицаОхватывает ряд различных подходов к принятию решений: от наиболее оптимистичного до наиболее пессимистичного (консервативного).
- 14. Пусть 0 ≤ α ≤ 1
- 15. При α = 0 критерий Гурвица становится
- 16. Пусть величины r(Аi, Sj) представляют затраты. Тогда наилучшим решением является то, которое обеспечивает
- 17. Пример.Национальная школа выживания подбирает место для строительства
- 18. Обозначения: А1 – А4 –
- 19. Критерий Лапласа. При P(S1) = ... = Р(S4)
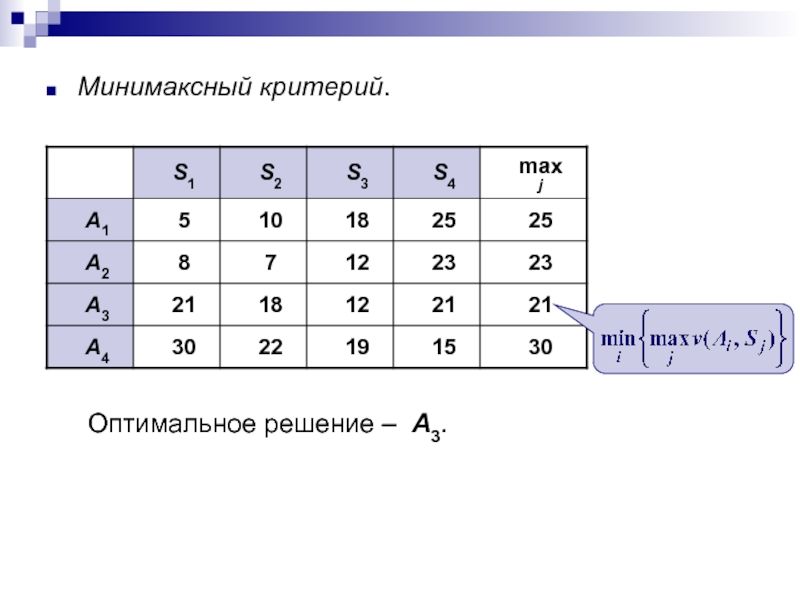
- 20. Минимаксный критерий. Оптимальное решение – А3.
- 21. Критерий Сэвиджа. Матрица рисков: Оптимальное решение – А2.
- 22. Критерий Гурвица. При α = 0,5 оптимальное решение
- 23. Теория игр (неопределенности противника)Ряд ЗПР обладает свойством:
- 24. Математическая модель конфликтной ситуации называется игрой. Заинтересованные стороны
- 25. Правила игры – система условий, описывающаявозможные действия
- 26. Если в игре участвуют два противника, то
- 27. Сравнение степеней удовлетворения интересов игрока в различных
- 28. Функция выигрыша игрока А каждой ситуации
- 29. Всякая игра полностью описывается совокупностью, состоящей измножества игроков,множеств их возможных стратегий,множества функций выигрыша игроков.
- 30. Оптимальной называется стратегия, которая при многократно повторяющейся
- 31. Если в парной игре выигрыш одного из
- 32. Пусть в конечной антагонистической игре известны значения
- 33. В конечной антагонистической игре матрица выигрышей игрока
- 34. Максиминные и минимаксные стратегииПри выборе стратегии Ai
- 35. Игрок А должен выбрать ту стратегию, которая имеет максимальный показатель эффективности или
- 36. Принцип выбора игроком А стратегии в соответствии
- 37. Если игрок А будет следовать максиминной стратегии,
- 38. Аналогичное рассуждение – в отношении игрока В,
- 39. Критерий выбора стратегии игрока В в соответствии
- 40. Пример. На каждой из двух торговых баз ассортиментный
- 41. Если магазин А завезет с базы товар
- 42. Игроки А и В – магазины А
- 43. Функция выигрыша игрока А: Матрица игры при n = 3:
- 44. Пусть c1 = c3 = 4, c2
- 45. Придерживаясь стратегий А2 или А3, игрок А
- 46. Свойство максиминных (минимаксных) стратегий – их неустойчивость. В
- 47. Ответный выбор игрока А – стратегия А1
- 48. Вывод: положение, при котором оба игрока пользуются
- 49. Решение игры с седловыми точкамиСитуация (Ai0, Вj0,),
- 50. Теорема. Ситуация (Ai0, Вj0) будет удовлетворительной для игрока
- 51. Ситуация (Ai0, Вj0) называется равновесной или ситуацией
- 52. Выигрыш аi0j0, соответствующий ситуации равновесия (Ai0, Вj0),
- 53. В примере выше:удовлетворительными для игрока А являются
- 54. Теорема. Для существования у матрицы игры седловой точки
- 55. Значение γ = α = β называется
- 56. Цена игры в чистых стратегиях γ (если
- 57. Пример. Финансовые компании А и В конкурируют между
- 58. Действие А1 приводит к отрицательному результату переговоров
- 59. Рассматриваемая ситуация – антагонистическая. Игрок А имеет
- 60. Нижняя и верхняя цена игры совпадают: α
- 61. Замечание. Матрица игры может обладать несколькими седловыми точками. Пример:
- 62. Соотношение между множествами минимаксных и оптимальных стратегий:каждая
- 63. Смешанные стратегииВ моделях практических конфликтов игры с
- 64. Игрок А: максиминная стратегия
- 65. Выход: образ действий, не сводящийся к выбору
- 66. Смешанная стратегия игрока представляет собой дискретную случайную
- 67. Смешанную стратегию Р игрока А можно отождествить
- 68. Теорема (основная теорема теории игр – фон
- 69. В общем случае не все чистые стратегии
- 70. Можно доказать, что решение игры обладает свойством: если
- 71. Сведение матричных игр к задачам ЛПМожно доказать:
- 72. и при ограничениях (2)
- 73. А именно: если оптимальное решение задачи (1), оптимальное решение
- 74. Замечание. Предположение о положительности элементов платежной матрицы не
- 75. Пример (рассмотрен выше). На каждой из двух торговых
- 76. Если магазин А завезет с базы товар
- 77. Игроки А и В – магазины А
- 78. Функция выигрыша игрока А: Матрица игры при n = 3:
- 79. Пусть c1 =1, c2 = 3, c3
- 80. Решение игры с матрицей А' равносильно решению
- 81. найти максимум φ(у1, у2, у3) = у1 + у2 + у3 при ограничениях
- 82. После приведения задачи 1) к канонической форме и применения симплекс метода:
- 83. Цена игры с матрицей А' оптимальная стратегия игрока А
- 84. Для игры с матрицей А оптимальная стратегия игрока А –
- 85. Для нахождения оптимальной стратегии игрока В можно, например, решить двойственную задачу 2).
- 86. Итоги:если магазин А будет завозить товары, выбирая
- 87. магазину В невыгодно отклоняться от своей оптимальной
- 88. В рассмотренном примере все чистые стратегии каждого из игроков активны. Такая игра называется полностью усредненной.
- 89. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2 Принятие решений в условиях неопределенности требует определения альтернативных действий, которым
соответствуют платежи (доход, затраты), зависящие от случайных состояний природы.
Слайд 3В случае m возможных действий (стратегий) и n состояний природы
матрицу платежей можно представить так:
Возможные решения
Состояния природы
Платежи
Слайд 4Отличие принятия решений в условиях неопределенности от принятия решений в
условиях риска:
вероятностное распределение, соответствующее состояниям Sj, j = 1,
2, …, n неизвестно (не может быть определено). Недостаток информации
Слайд 5Критерии для анализа ситуации, связанной с принятием решений в условиях
неопределенности:
критерий Лапласа;
максиминный (минимаксный) критерий;
критерий Сэвиджа;
критерий Гурвица.
Отличаются степенью консерватизма, который
проявляет ЛПР перед лицом неопределенности.Слайд 6Критерий Лапласа
Опирается на принцип недостаточного основания:
распределение вероятностей состояний
Sj, j
= 1, 2, …, n неизвестно нет
причин считать эти вероятности различными.Используется оптимистическое предположение, что вероятности всех состояний природы равны между собой:
P(S1) = P(S2) = ... = Р(Sn) = 1/n.
Слайд 7Если при этом
v(Аi, Sj) представляет получаемую прибыль, то наилучшим
решением является то, которое обеспечивает
v(Аi, Sj) представляет расходы ЛПР, то
наилучшим решением является то, которое обеспечиваетСлайд 8Максиминный (минимаксный) критерий
Основан на консервативном осторожном поведении ЛПР и сводится
к выбору наилучшей альтернативы из наихудших.
Слайд 9Если
v(Аi, Sj) представляет получаемую прибыль, то наилучшим решением является то,
которое обеспечивает
v(Аi, Sj) представляет расходы ЛПР, то наилучшим решением является
то, которое обеспечиваетСлайд 10Критерий Сэвиджа
Попытка смягчить консерватизм максиминного (минимаксного) критерия путем замены
матрицы платежей (выигрышей или проигрышей) v(Аi, Sj) матрицей потерь (матрицей
рисков) r(Аi, Sj):Слайд 11Пример.
Матрица платежей (расходов):
Согласно минимаксному критерию решение А2 с фиксированными потерями
в $10 000 является предпочтительным.
Но: при выборе А1 имеется возможность
потерять только $90, если реализуется состояние S2.Слайд 12Составим матрицу потерь (матрицу рисков):
Согласно минимаксному критерию, примененному к матрице
потерь, решение А1 является предпочтительным.
Слайд 13Критерий Гурвица
Охватывает ряд различных подходов к принятию решений:
от наиболее оптимистичного
до наиболее пессимистичного (консервативного).
Слайд 14Пусть 0 ≤ α ≤ 1 и величины r(Аi,
Sj) представляют доходы.
Тогда наилучшим решением является то, которое обеспечивает
Параметр α
называется показателем оптимизма.Выбор величины конкретизирует степень оптимизма (пессимизма) ЛПР.
Слайд 15При α = 0 критерий Гурвица становится консервативным (его применение
эквивалентно применению максиминного критерия).
При α = 1 критерий Гурвица
становится слишком оптимистичным (рассчитывает на наилучшие из наилучших условий). При отсутствии ярко выраженной склонности к оптимизму или пессимизму выбор α = 0,5 представляется наиболее разумным.
Слайд 16Пусть величины r(Аi, Sj) представляют затраты.
Тогда наилучшим решением является то,
которое обеспечивает
Слайд 17Пример.
Национальная школа выживания подбирает место для строительства летнего лагеря для
тренировки людей на выживание в условиях дикой природы.
Школа считает,
что число участников сбора может быть 200, 250, 300 или 350 человек. Стоимость лагеря должна быть минимальной (строится для удовлетворения точно определенных небольших потребностей).
Отклонение в сторону уменьшения или увеличения относительно заданного уровня потребностей влечет дополнительные затраты (строительство неиспользуемых мощностей или потеря возможности получения прибыли в случае, когда некоторые потребности не удовлетворяются).
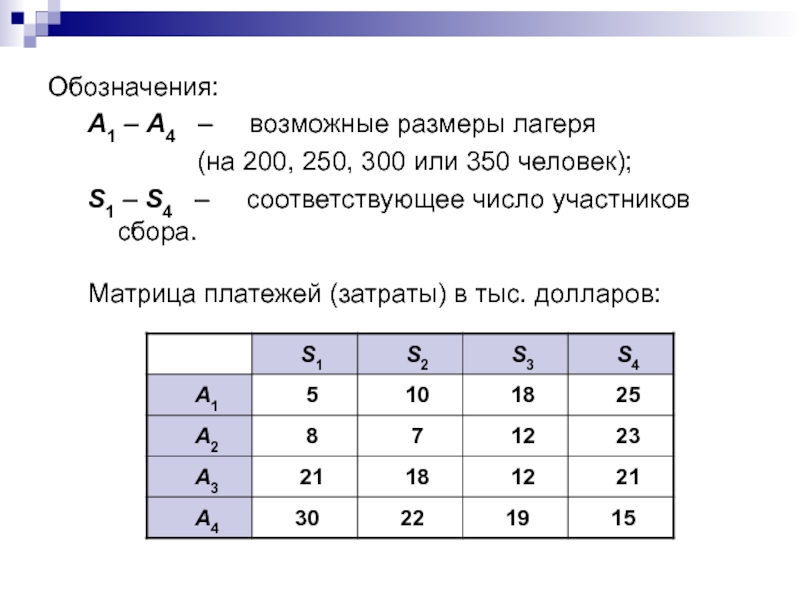
Слайд 18Обозначения:
А1 – А4 – возможные размеры лагеря
(на 200, 250, 300 или 350 человек);
S1
– S4 – соответствующее число участников сбора. Матрица платежей (затраты) в тыс. долларов:
Слайд 19Критерий Лапласа.
При P(S1) = ... = Р(S4) = 1/4 ожидаемые
значения затрат равны
М(А1) = 1/4 ∙ (5 + 10 +
18 + 25) = 14,5 М(А2) = 1/4 ∙ (8 + 7 + 12 + 23) = 12,5
М(А3) = 1/4 ∙ (21 + 18 + 12 + 21) = 18
М(А4) = 1/4 ∙ (30 + 22 + 19 + 15) = 21,5 .
Оптимальное решение – А2.
min
Слайд 22Критерий Гурвица.
При α = 0,5 оптимальное решение – А1 или
А2;
При α = 0,25 оптимальное решение – А3.
Слайд 23Теория игр (неопределенности противника)
Ряд ЗПР обладает свойством:
столкновение не менее
двух сторон с различными (возможно, противоположными) интересами;
каждая сторона имеет
возможность действовать различными способами, причем выбор способа может осуществляться в зависимости от действий противоборствующей стороны. Такие ситуации называются конфликтными.
Слайд 24Математическая модель конфликтной ситуации называется игрой.
Заинтересованные стороны (потребители, предприятия, финансовые
союзы, индивидуумы) в игре называются игроками.
При формализации конфликтной ситуации несущественные
факторы отбрасываются; ее протекание ограничивается определенными правилами.Слайд 25Правила игры – система условий, описывающая
возможные действия каждого из игроков;
объем
информации, которую может получить каждая сторона о действиях другой стороны;
последовательность
чередования «ходов» (отдельных решений, принятых в процессе игры);исход игры в результате каждой совокупности ходов противников.
Любое возможное в игре действие игрока называется его стратегией (чистой стратегией).
Слайд 26Если в игре участвуют два противника, то игра называется парной.
Обозначения:
множество всех стратегий
игрока А, множество всех стратегий игрока В,
упорядоченная пара х = (Ai, Bj) – ситуация: в результате очередного хода игроки выбрали стратегии Ai и Bj соответственно.
Слайд 27Сравнение степеней удовлетворения интересов игрока в различных ситуациях – путем
введения отношения предпочтения данного игрока.
Математически: отношение частичного порядка на множестве
всех ситуаций.
Слайд 28Функция выигрыша игрока А
каждой ситуации
ставит в соответствие некоторое число, называемое выигрышем игрока
А в ситуации х.Характеризует степень удовлетворения интересов игрока А
Слайд 29Всякая игра полностью описывается совокупностью, состоящей из
множества игроков,
множеств их возможных
стратегий,
множества функций выигрыша игроков.
Слайд 30Оптимальной называется стратегия, которая при многократно повторяющейся игре гарантирует игроку
максимально возможный средний выигрыш (минимально возможный средний проигрыш).
Выбор этой стратегии
базируется на предположении: оба игрока разумны в одинаковой степени и поведение каждого из них направлено на противодействие противнику в достижении его целей (абстрагируется от просчетов, азарта и т. п.).Может пониматься в различных смыслах в зависимости от показателя оптимальности
Слайд 31Если в парной игре выигрыш одного из игроков равен проигрышу
другого игрока, т. е.
то игра называется игрой с
нулевой суммой или антагонистической (интересы игроков противоположны).Антагонистическая игра полностью определяется совокупностью
Слайд 32Пусть в конечной антагонистической игре известны значения
выигрыш (проигрыш) игрока
А в ситуации (Ai, Bj).
Матрица выигрышей игрока А:
Слайд 33В конечной антагонистической игре матрица выигрышей игрока В
В = –АТ,
игра может быть охарактеризована только одной матрицей
выигрышей. Такая игра называется матричной; матрица А называется также матрицей игры или платежной матрицей.
Слайд 34Максиминные и минимаксные стратегии
При выборе стратегии Ai игрок А может
получить один из выигрышей
ai1, ai2, … , ain
в зависимости от
стратегии, выбранной игроком B.Считаем, что игрок В выбирает оптимальную для себя стратегию (ту, при которой выигрыш игрока А минимален).
показатель эффективности стратегии Ai.
Слайд 35Игрок А должен выбрать ту стратегию, которая имеет максимальный показатель
эффективности
или
Слайд 36Принцип выбора игроком А стратегии в соответствии со (*) называется
максиминным принципом, а выигрыш
α – максимином.Стратегия Ai0, соответствующая максимину α (имеющая максимальный показатель эффективности), называется максиминной стратегией игрока А.
Это наиболее осторожная («перестраховочная») стратегия
Слайд 37Если игрок А будет следовать максиминной стратегии, то при любой
игре игрока В игроку А будет гарантирован выигрыш не менее
α.Поэтому максимин α, определенный в соответствии со (*), называется нижней ценой игры в чистых стратегиях.
Слайд 38Аналогичное рассуждение – в отношении игрока В, который стремится минимизировать
выигрыш игрока А, исходя из посылки, что А играет наилучшим
для себя и наихудшим для В образом:показатель неэффективности стратегии Вi,
или
Слайд 39Критерий выбора стратегии игрока В в соответствии с (**) называется
минимаксным принципом,
а выигрыш β – минимаксом или верхней ценой игры.Стратегия Вj0, соответствующая минимаксу β, называется минимаксной стратегией игрока В.
Если игрок В будет придерживаться наиболее острожной минимаксной стратегии, то при любых действиях игрока А проигрыш В будет не более β.
Можно показать:
α ≤ β.
Слайд 40Пример.
На каждой из двух торговых баз ассортиментный минимум составляет один
и тот же набор из n видов товара.
Каждая база
поставляет в свой магазин только один из этих видов товара, причем один и тот же вид товара продается в обоих магазинах по одной и той же цене. Магазины А и В конкурируют между собой.
Товар, поставляемый в магазин В, более высокого качества.
Слайд 41 Если магазин А завезет с базы товар i-го вида, отличный
от товара j-го вида, завезенного в магазин В, то товар
i-го вида будет пользоваться спросом, и магазин получит прибыль от его реализации в размере ci денежных единиц.Если в магазины А и В завезены товары одного и того же вида i = j, то магазин А понесет убытки (стоимость транспортировки, хранения и, возможно, порча товара) в размере di денежных единиц.
Формализуем конфликтную ситуацию и построим матрицу игры при n = 3.
Слайд 42Игроки А и В – магазины А и В.
Стратегии игрока
А:
A1, A2, …, An – завоз со своей базы
товара i-го вида, i = 1, 2, …, n. Стратегии игрока В:
B1, B2, …, Bn – завоз со своей базы товара j-го вида, j = 1, 2, …, n.
Слайд 44Пусть c1 = c3 = 4, c2 = 1, d1
= 3, d2 = d3 = 2.
Тогда
Стратегии А2 и
А3 игрока А являются максиминными,каждая из стратегий игрока В является минимаксной.
Слайд 45 Придерживаясь стратегий А2 или А3, игрок А проиграет не более
2 денежных единиц;
игрок В при выборе любой стратегии проигрывает
не более 4 денежных единиц. Нижняя цена игры
верхняя цена игры
Слайд 46 Свойство максиминных (минимаксных) стратегий – их неустойчивость.
В примере выше:
пусть игрок
А придерживается максиминной стратегии, например, А2.
Предположим, что это стало
известно игроку В. В, желая получить наибольший выигрыш (наибольший проигрыш А – минимум по второй строке), выберет стратегию В2.
Слайд 47 Ответный выбор игрока А – стратегия А1 или А3 (максимум
по второму столбцу).
Пусть выбрана стратегия А3.
Игрок В выбирает стратегию
В3 – отклоняется от своей предыдущей стратегии. Игрок А должен выбрать стратегию А1 (также отклонившись от выбранной ранее стратегии).
И т. д.
(A2, B2) → (A3, B2) → (A3, B3) → (A1, B3) → (A1, B1) → …
Слайд 48Вывод:
положение, при котором оба игрока пользуются своими минимаксными стратегиями,
неустойчиво, и может быть нарушено поступившими сведениями о стратегии противной
стороны.Слайд 49Решение игры с седловыми точками
Ситуация (Ai0, Вj0,), сложившаяся в результате
выбора игроками А и В стратегий Ai0 и Вj0 соответственно,
называется удовлетворительной (приемлемой, допустимой) для игрока А, еслии удовлетворительной для игрока В, если
Слайд 50Теорема.
Ситуация (Ai0, Вj0) будет удовлетворительной для игрока А тогда и
только тогда, когда его выигрыш аi0j0 совпадает с показателем неэффективности
βj0 стратегии Вj0 игрока В:(максимум в j0-м столбце матрицы игры);
ситуация (Ai0, Вj0) будет удовлетворительной для игрока В тогда и только тогда, когда его проигрыш аi0j0 совпадает с показателем эффективности αi0 стратегии Аi0 игрока А:
(минимум в i0-й строке матрицы игры).
Слайд 51 Ситуация (Ai0, Вj0) называется равновесной или ситуацией равновесия, если она
удовлетворительна для каждого из игроков А и В.
Из теоремы:
(Ai0, Вj0) – ситуация равновесия в том и только в том случае, когдаСлайд 52 Выигрыш аi0j0, соответствующий ситуации равновесия (Ai0, Вj0), называется седловой точкой
матрицы игры.
Игра, матрица которой содержит хотя бы одну седловую
точку, называется игрой с седловой точкой. Слайд 53В примере выше:
удовлетворительными для игрока А являются ситуации (A3, B1),
(A1, B2), (A3, B2) и (A1, B3);
для игрока В
– ситуации (A1, B1), (A2, B2) и (A3, B3);не существует ситуации, удовлетворительной для обоих игроков не существует равновесной ситуации.
Данная игра является игрой без седловых точек.
Слайд 54Теорема.
Для существования у матрицы игры седловой точки необходимо и достаточно,
чтобы нижняя цена игры равнялась ее верхней цене:
α = β. Слайд 55Значение γ = α = β называется ценой игры в
чистых стратегиях (ценой игры).
Стратегии Ai0 и Вj0 игроков А и
В, создающие равновесную ситуацию (Ai0, Вj0) (соответствующие седловой точке аi0j0), называются оптимальными, а их совокупность – решением игры.Решение игры характеризуется свойством:
ни одному из игроков, придерживающихся своей оптимальной стратегии, невыгодно от нее отклоняться.
Слайд 56Цена игры в чистых стратегиях γ (если она существует) –
это значение выигрыша игрока А, которое он не может увеличить,
если игрок В придерживается своей оптимальной стратегии;и значение проигрыша игрока В, которое он не может уменьшить, если игрок А придерживается своей оптимальной стратегии.
Слайд 57Пример.
Финансовые компании А и В конкурируют между собой.
Компания В
ведет переговоры с организаторами трех инвестиционных проектов B1, B2, B3
на предмет инвестирования.Компания А ставит своей задачей срыв переговоров, чтобы занять место компании В в инвестировании.
Для достижения этой цели она может применить одно из двух средств:
А1 – предложить организаторам проектов более выгодные для них условия инвестирования;
А2 – предоставить организаторам проектов материалы, компрометирующие компанию В.
Слайд 58 Действие А1 приводит к отрицательному результату переговоров с организаторами проектов
B1, B2, B3 с вероятностями 0,7; 0,5 и 0,3 соответственно;
действие А2 – с вероятностями 0,6; 0,9 и 0,4.Формализуем эту конфликтную ситуацию.
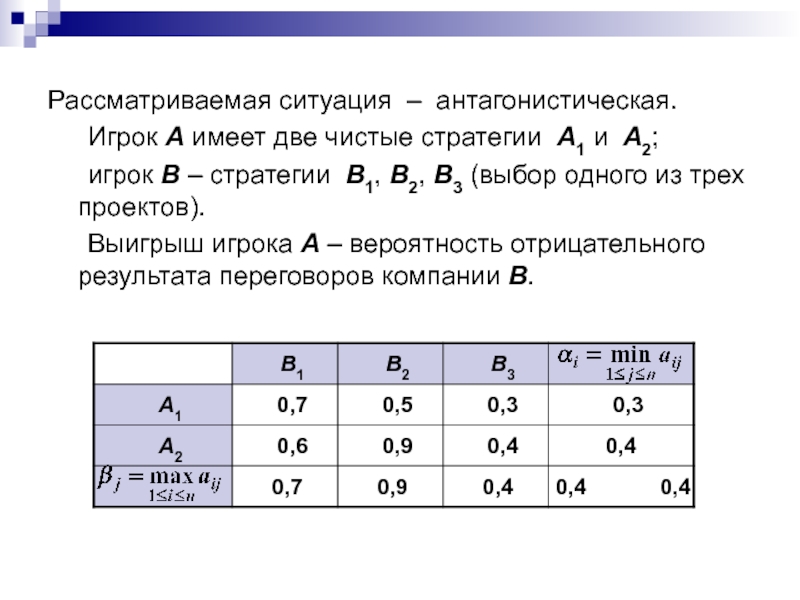
Слайд 59Рассматриваемая ситуация – антагонистическая.
Игрок А имеет две чистые стратегии
А1 и А2;
игрок В – стратегии B1, B2, B3
(выбор одного из трех проектов). Выигрыш игрока А – вероятность отрицательного результата переговоров компании В.
Слайд 60Нижняя и верхняя цена игры совпадают: α = β =
0,4.
Это значение – цена игры в чистых стратегиях (седловая точка
игры). Ситуация (A2, B3) является равновесной.
Оптимальные стратегии:
для игрока А – стратегия А2;
для игрока В – стратегия B3.
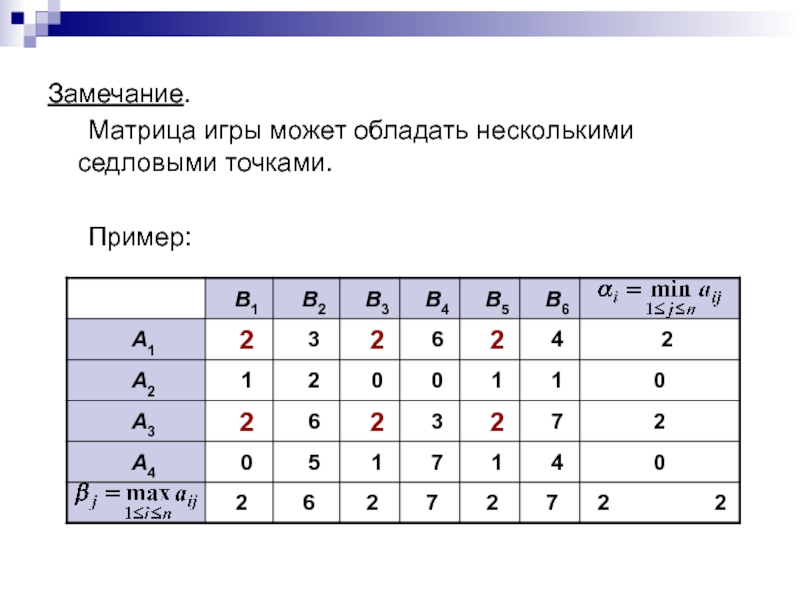
Слайд 62Соотношение между множествами минимаксных и оптимальных стратегий:
каждая оптимальная стратегия игрока
А является его максиминной стратегией; каждая оптимальная стратегия игрока В
является его минимаксной стратегией;в игре без седловых точек ни одна из максиминных и минимаксных стратегий не является оптимальной (в такой игре вообще нет оптимальных стратегий);
в игре с седловыми точками каждая максиминная и каждая минимаксная стратегия является оптимальной.
Слайд 63Смешанные стратегии
В моделях практических конфликтов игры с седловой точкой встречаются
сравнительно редко;
более типичная ситуация: нижняя и верхняя цена игры
различны. Слайд 64Игрок А: максиминная стратегия гарантия выигрыша не
меньше нижней цены игры;
игрок В: минимаксная стратегия
гарантия проигрыша не больше верхней цены игры. При многократном повторении игры каждый игрок
получает информацию о предыдущих ходах противника,
хочет скрыть от противника свои намерения.
Слайд 65Выход:
образ действий, не сводящийся к выбору единственной чистой стратегии;
цель – увеличение гарантированного среднего выигрыша.
Комбинированная стратегия игрока, состоящая в
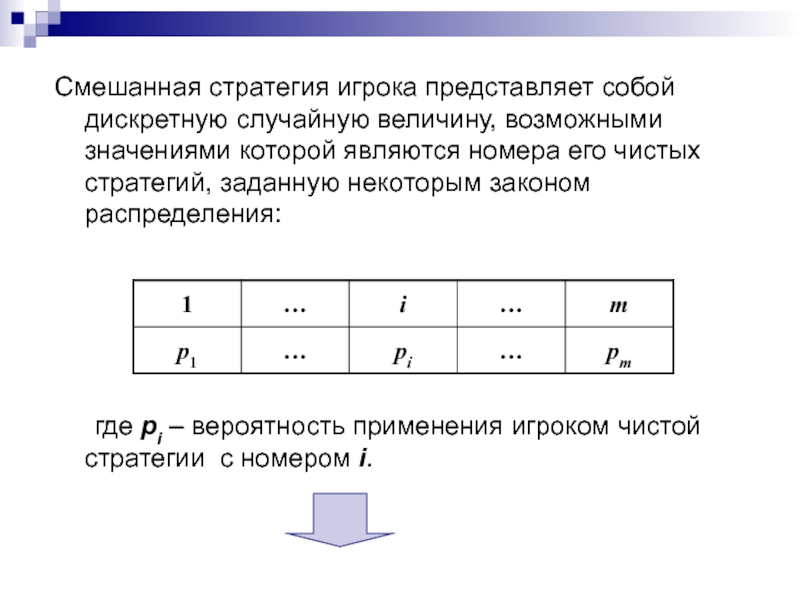
применении нескольких чистых стратегий, чередующихся по случайному закону, называется смешанной стратегией. Слайд 66Смешанная стратегия игрока представляет собой дискретную случайную величину, возможными значениями
которой являются номера его чистых стратегий, заданную некоторым законом распределения:
где
pi – вероятность применения игроком чистой стратегии с номером i.Слайд 67Смешанную стратегию Р игрока А можно отождествить с m-мерным вектором
(р1, р2, …, рm),
смешанную стратегию Q игрока B –
с n-мерным вектором (q1, q2, …, qn).Если игроки А и В независимо друг от друга выбрали смешанные стратегии Р = (р1, р2, …, рm) и Q = (q1, q2, …, qn), то упорядоченная пара (Р, Q) называется ситуацией в смешанных стратегиях.
Слайд 68Теорема (основная теорема теории игр – фон Нейман, 1928 г.).
Любая матричная игра имеет решение в смешанных стратегиях, т. е.
существуют цена игры V в смешанных стратегиях и оптимальные смешанные стратегии P0 и Q0 игроков А и В соответственно. Очевидно, что
α ≤ V ≤ β.
Слайд 69В общем случае не все чистые стратегии игрока входят в
его оптимальную смешанную стратегию с положительными вероятностями.
Чистые стратегии, входящие
в оптимальную смешанную стратегию игрока с положительными вероятностями, называют его активными стратегиями. Слайд 70Можно доказать, что решение игры обладает свойством:
если один из игроков
придерживается своей оптимальной смешанной стратегии, то выигрыш остается неизменным и
равным цене игры V, независимо от действий другого игрока, если только этот игрок придерживается любой своей чистой активной стратегии.Слайд 71Сведение матричных игр к задачам ЛП
Можно доказать:
решение любой матричной
игры с положительными элементами платежной матрицы эквивалентно решению пары двойственных
задач ЛПпри ограничениях (1)
Слайд 73А именно:
если
оптимальное решение задачи (1),
оптимальное решение задачи (2),
то
цена игры
с матрицей А;
оптимальная стратегия игрока А;
оптимальная стратегия игрока В.
Слайд 74Замечание.
Предположение о положительности элементов платежной матрицы не умаляет общности рассуждений:
матрица с любыми элементами может быть приведена к матрице с
положительными элементами с помощью преобразованияа'ij = аij + λ,
При этом оптимальные стратегии не изменятся, а цена игры увеличится на λ.
Слайд 75Пример (рассмотрен выше).
На каждой из двух торговых баз ассортиментный минимум
составляет один и тот же набор из n видов товара.
Каждая база поставляет в свой магазин только один из этих видов товара, причем один и тот же вид товара продается в обоих магазинах по одной и той же цене.
Магазины А и В конкурируют между собой.
Товар, поставляемый в магазин В, более высокого качества.
Слайд 76 Если магазин А завезет с базы товар i-го вида, отличный
от товара j-го вида, завезенного в магазин В, то товар
i-го вида будет пользоваться спросом, и магазин получит прибыль от его реализации в размере ci денежных единиц.Если в магазины А и В завезены товары одного и того же вида i = j, то магазин А понесет убытки (стоимость транспортировки, хранения и, возможно, порча товара) в размере di денежных единиц.
Слайд 77Игроки А и В – магазины А и В.
Стратегии игрока
А:
A1, A2, …, An – завоз со своей базы
товара i-го вида, i = 1, 2, …, n. Стратегии игрока В:
B1, B2, …, Bn – завоз со своей базы товара j-го вида, j = 1, 2, …, n.