Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Признак параллельности прямых по сумме градусных мер односторонних углов
Содержание
- 1. Признак параллельности прямых по сумме градусных мер односторонних углов
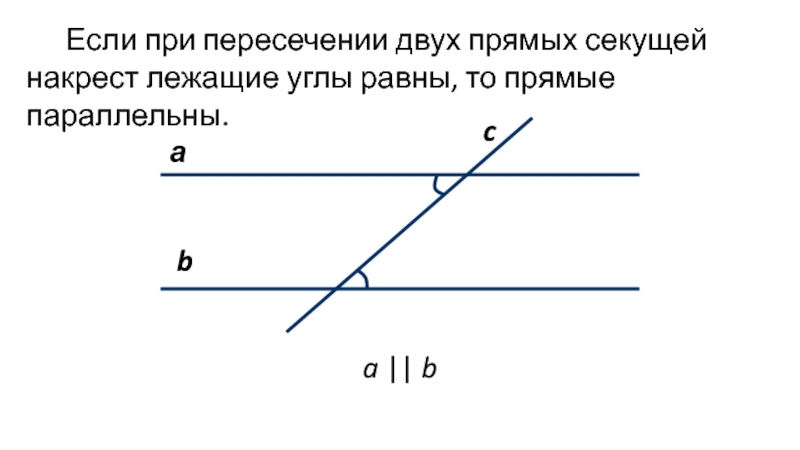
- 2. Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.аcba || b
- 3. Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.аca || bb
- 4. Теорема. Если при пересечении двух прямых секущей
- 5. Задача. При пресечении двух параллельных прямых а
- 6. Задача. В треугольнике АВС стороны АВ и
- 7. Задача. В треугольнике АВС градусная мера ∠
- 8. Скачать презентанцию
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.аcba || b
Слайды и текст этой презентации
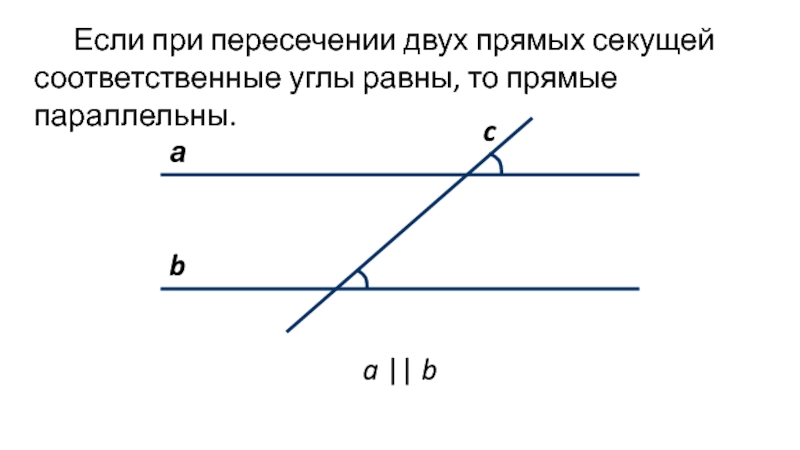
Слайд 3Если при пересечении двух прямых секущей соответственные углы равны, то
прямые параллельны.
а
c
a || b
b
Слайд 4Теорема. Если при пересечении двух прямых секущей сумма градусных мер
односторонних углов равна 180°, то прямые параллельны.
Доказательство.
то ∠ 2
+ ∠ 3 = 180°.Следовательно, ∠ 1 = ∠ 3.
Так как ∠ 1 и ∠ 3 – накрест лежащие,
то а || b.
Теорема доказана.
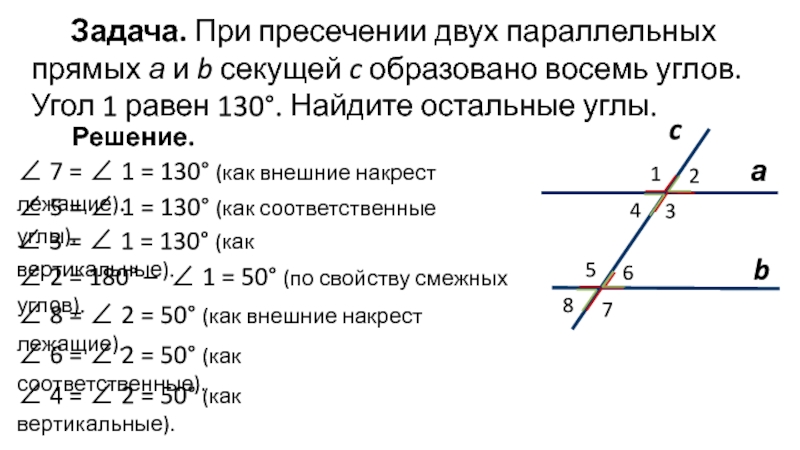
Слайд 5Задача. При пресечении двух параллельных прямых а и b секущей
c образовано восемь углов. Угол 1 равен 130°. Найдите остальные
углы.Решение.
а
c
b
2
1
3
4
6
5
8
7
∠ 7 = ∠ 1 = 130° (как внешние накрест лежащие).
∠ 5 = ∠ 1 = 130° (как соответственные углы).
∠ 3 = ∠ 1 = 130° (как вертикальные).
∠ 2 = 180° – ∠ 1 = 50° (по свойству смежных углов).
∠ 8 = ∠ 2 = 50° (как внешние накрест лежащие).
∠ 6 = ∠ 2 = 50° (как соответственные).
∠ 4 = ∠ 2 = 50° (как вертикальные).
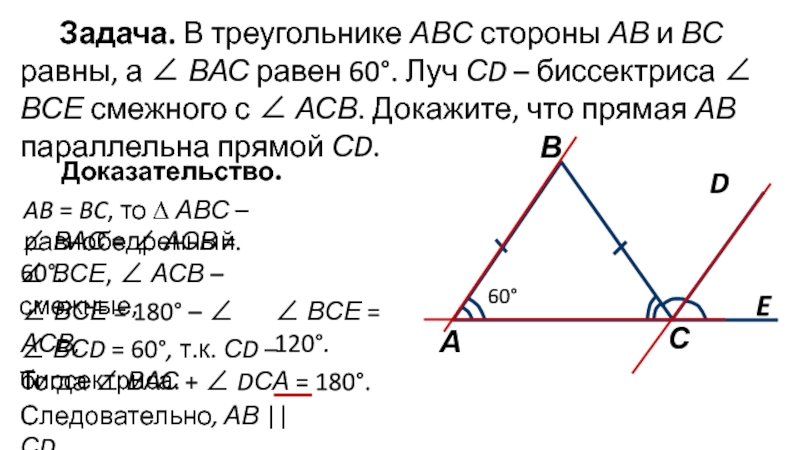
Слайд 6Задача. В треугольнике АВС стороны АВ и ВС равны, а
∠ ВАС равен 60°. Луч СD – биссектриса ∠ ВСЕ
смежного с ∠ АСВ. Докажите, что прямая АВ параллельна прямой СD.Доказательство.
А
В
С
60°
E
D
AB = BC, то ∆ АВС – равнобедренный.
∠ ВАС = ∠ АСВ = 60°.
∠ ВСЕ, ∠ АСВ – смежные,
∠ ВСЕ = 180° – ∠ АСВ,
∠ ВСЕ = 120°.
∠ ВСD = 60°, т.к. СD – биссектриса.
Тогда ∠ ВАС + ∠ DСА = 180°.
Следовательно, АВ || СD .
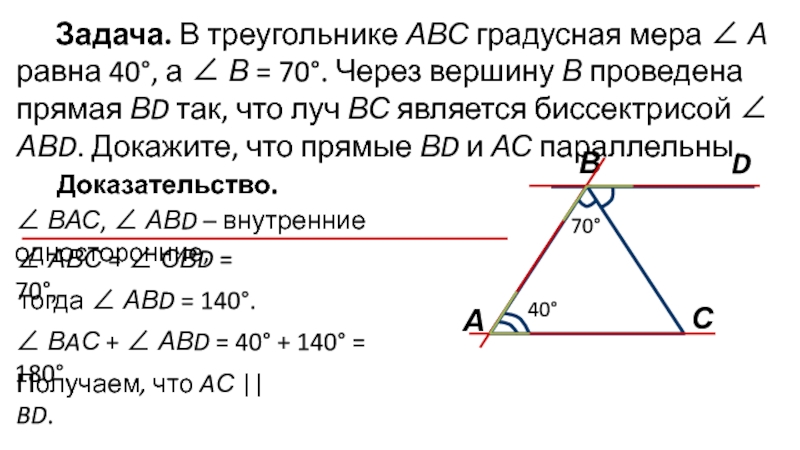
Слайд 7Задача. В треугольнике АВС градусная мера ∠ А равна 40°,
а ∠ В = 70°. Через вершину В проведена прямая
ВD так, что луч ВС является биссектрисой ∠ АВD. Докажите, что прямые ВD и АС параллельны.Доказательство.
А
В
С
40°
70°
D
∠ ВАС, ∠ АВD – внутренние односторонние,
∠ АВС = ∠ СВD = 70°,
тогда ∠ АВD = 140°.
∠ ВAС + ∠ АВD = 40° + 140° = 180°.
Получаем, что AС || BD.
