ПРОЕКЦИЯ СИЛЫ НА ОСЬ И НА ПЛОСКОСТЬ

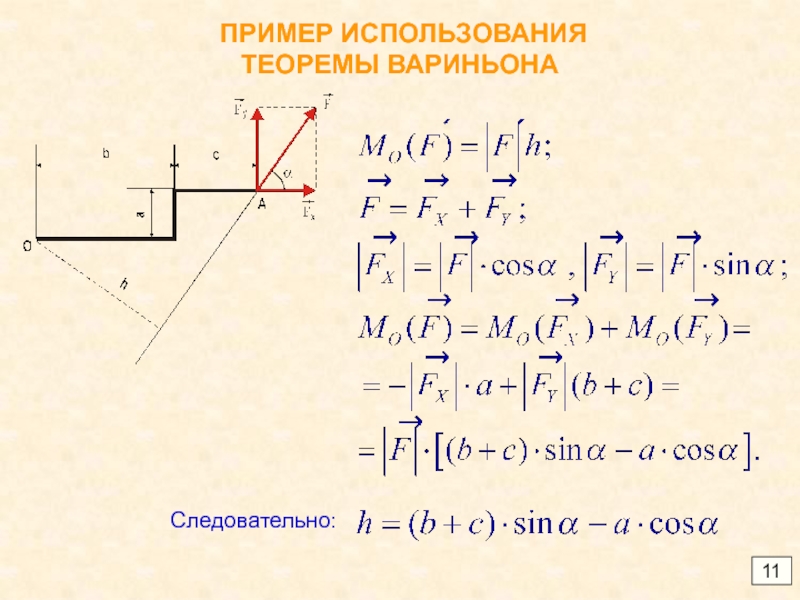
силы на ось есть скалярная величина, равная взятой с
соответствующим

знаком длине отрезка, заключенного между проекциями
начала и конца силы на данную ось.
Проекция на ось имеет знак «+» если перемещение от ее начала к
концу совпадает с положительным направлением оси и знак «» в
противном случае.
Проекцию силы на ось можно вычислить аналитически как произведе-
ние модуля силы на косинус угла между направлением силы и положи-
тельным направлением оси.

двойного проектирования используется
в тех случаях, когда для нахождения проекции
силы

на ось бывает удобнее сначала найти ее
проекцию на координатную плоскость, в которой
лежит эта ось, а затем найденную проекцию
силы на плоскость спроектировать на данную ось

систему сил, в которой линии действия всех сил пересекаются в

одной точке.
Следует различать плоскую систему сходящихся сил, в которой линии действия всех сил лежат в одной плоскости, и пространственную систему сходящихся сил, в которой линии действия сил не лежат в одной плоскости.

Всякая система сходящихся сил может быть заменена одной силой –
равнодействующей.

Замечание. Модуль и направление равнодействующей определяются однозначно и
не зависят от порядка, в котором складываются силы. Задача о разложении
равнодействующей на составляющие однозначного решения не имеет!

необходимо и достаточно, чтобы
равнодействующая данной системы сил была равна

нулю.
Геометрически это означает, что силовой многоугольник, построенный на
силах системы, должен быть замкнут!

Условия равновесия системы сходящихся сил:

аналитическая форма

находится в равновесии под действием
трех непараллельных сил, лежащих в одной

плоскости, то линии действия этих сил пересекаются в одной точке.

Доказательство

Замечание. Обратная теорема не имеет места!

Теорема о трех силах позволяет определить заранее неизвестное
направление реакции неподвижного шарнира в точке А:

статически определимой если число неизвестных
задачи не превышает числа уравнений

равновесия, даваемых статикой
твердого тела для данного вида системы сил.
В противном случае задачу называют статически неопределимой.

Замечание. Статическая неопределимость задачи может появиться за счет
Наложения “лишних” связей, не нужных для обеспечения равновесия АТТ.
Расчет статически неопределимых систем требует учета деформаций и
рассматривается в сопротивлении материалов и теории упругости.

ПРИМЕРЫ

Статически определимые задачи

Статически неопределимая задача

на плоскости (алгебраическим
моментом) называют скалярную величину, равную взятому со

знаком «+»
или «» произведению модуля силы на плечо - кратчайшее расстояние от
точки до линии действия силы.

Момент силы характеризует вращательный эффект действия силы на
твердое тело.
Различают:
момент силы относительно точки на плоскости;
момент силы относительно центра в пространстве;
момент силы относительно оси.

Правило знаков: в теоретической механике момент силы считают поло-
жительным, если сила стремится повернуть тело вокруг точки против хода
часовой стрелки и отрицательным, если по часовой стрелке

изменяется при переносе силы
по линии ее

действия.

2) Момент силы равен нулю если плечо силы h=0.

сходящихся сил относи-
тельно некоторой точки, лежащей в плоскости сил, равен

алгебраичес-
кой сумме моментов сил системы относительно той же точки.

Доказательство: