с помощью производной
Необходимое условие экстремума функции
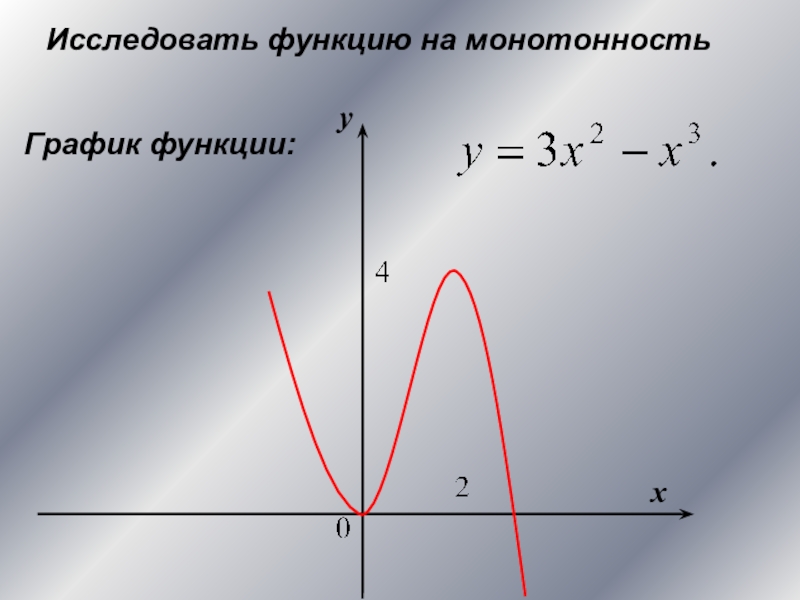
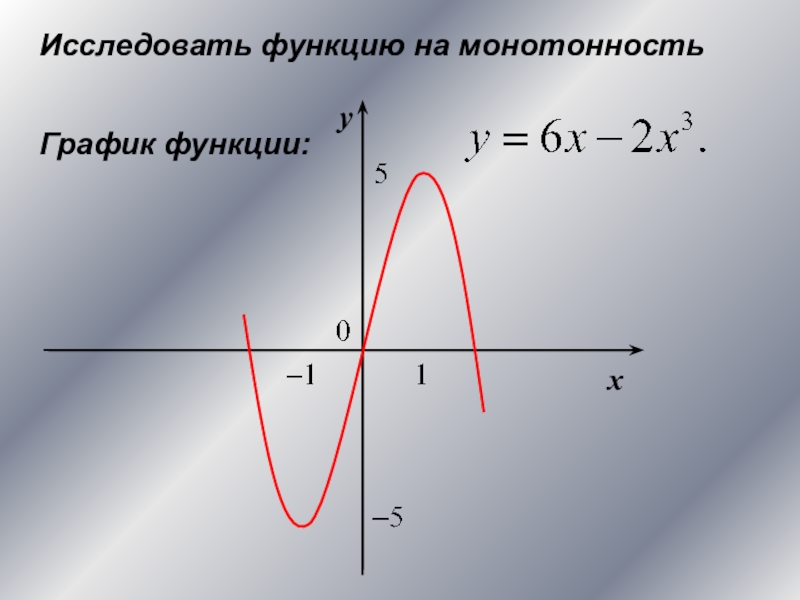
Алгоритм исследования функции на
монотонность и экстремумыЗадачи на исследование функций на монотонность