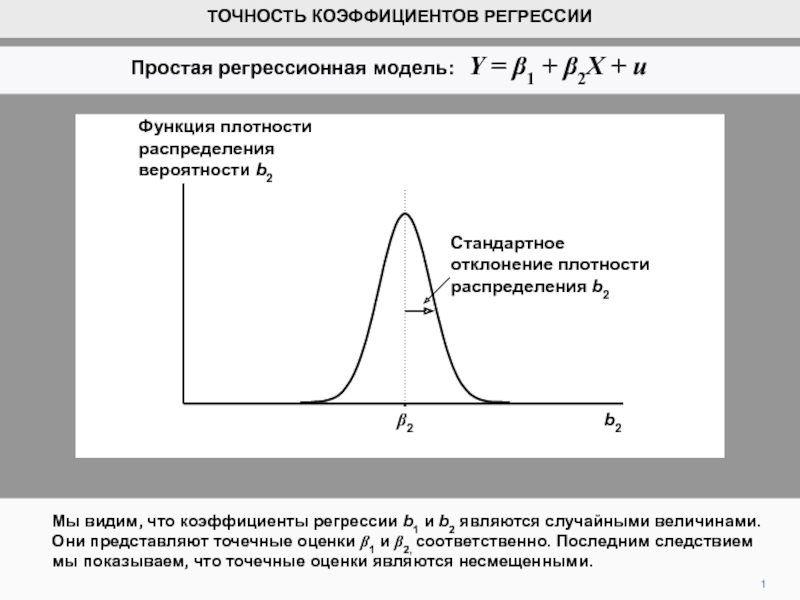
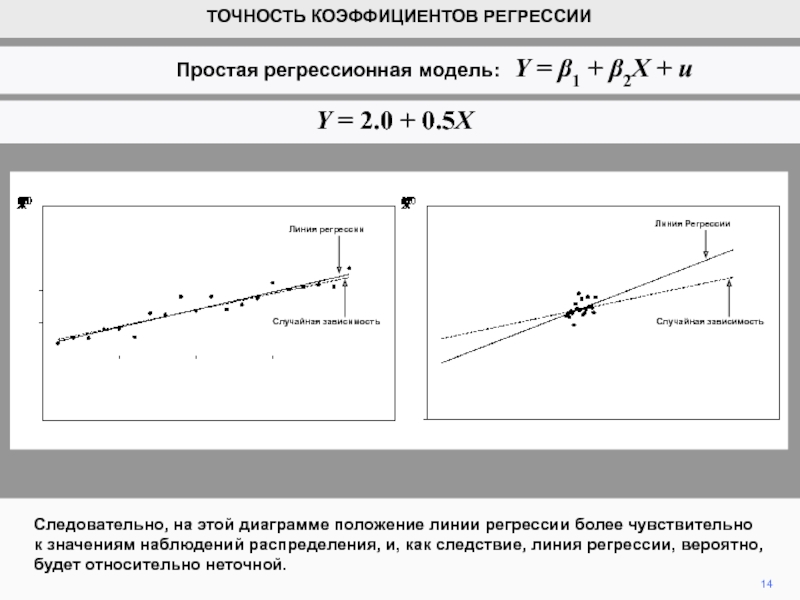
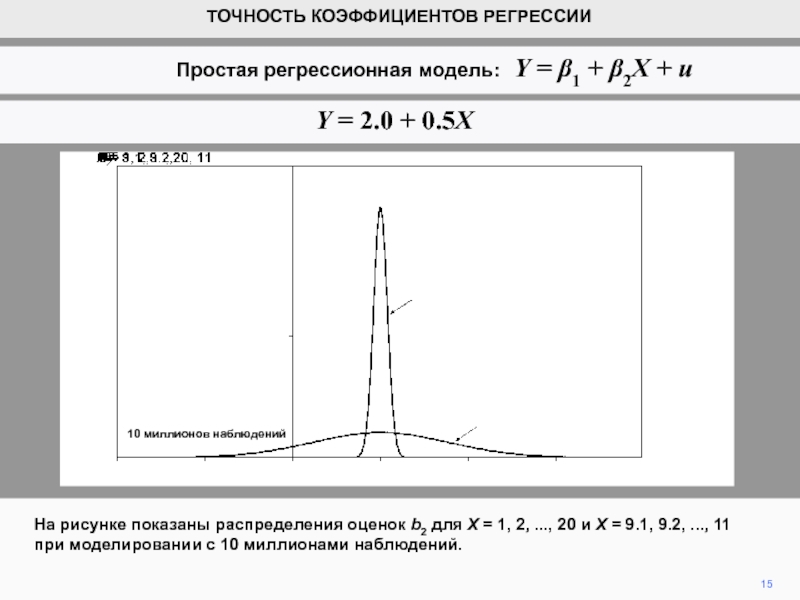
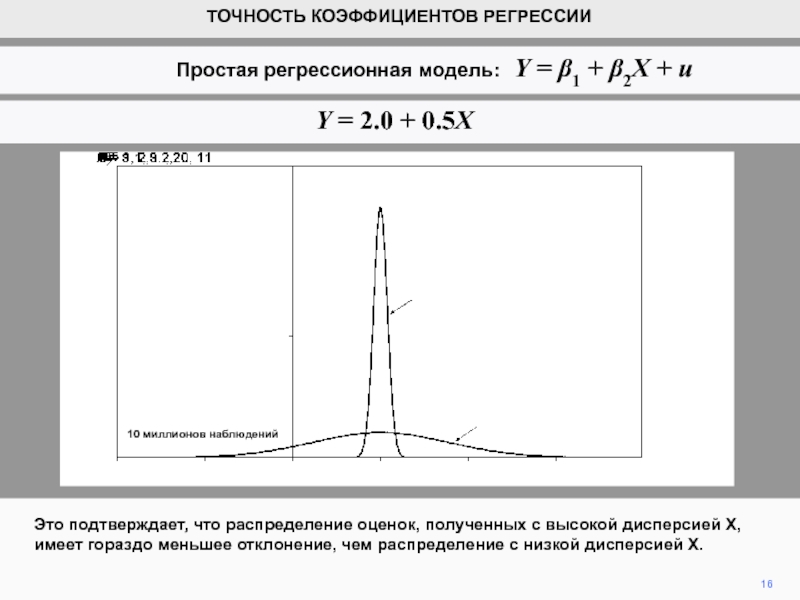
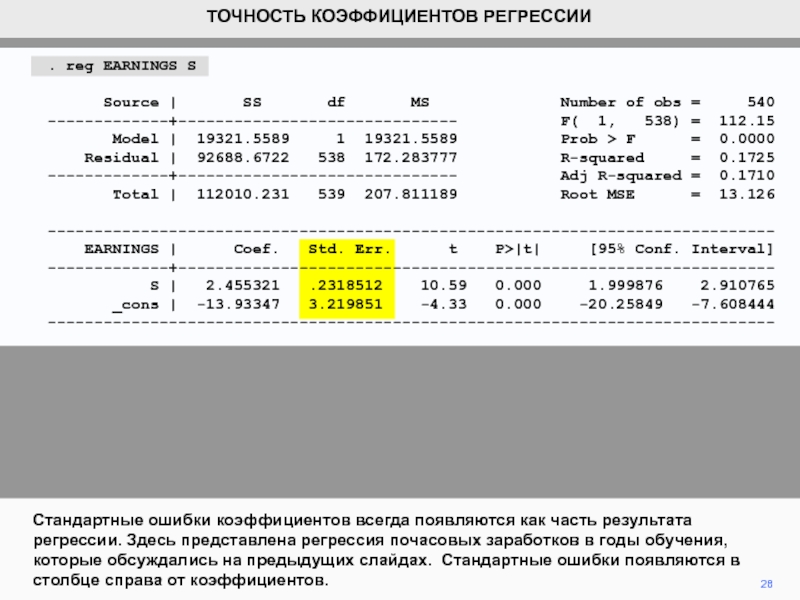
видим, что коэффициенты регрессии b1 и b2 являются случайными величинами.
Они представляют точечные оценки b1 и b2, соответственно. Последним следствием мы показываем, что точечные оценки являются несмещенными.ТОЧНОСТЬ КОЭФФИЦИЕНТОВ РЕГРЕССИИ
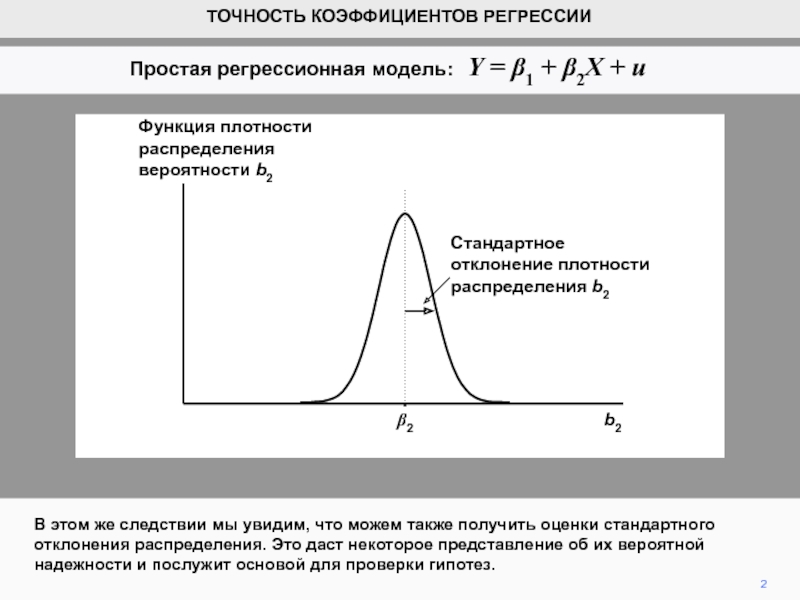
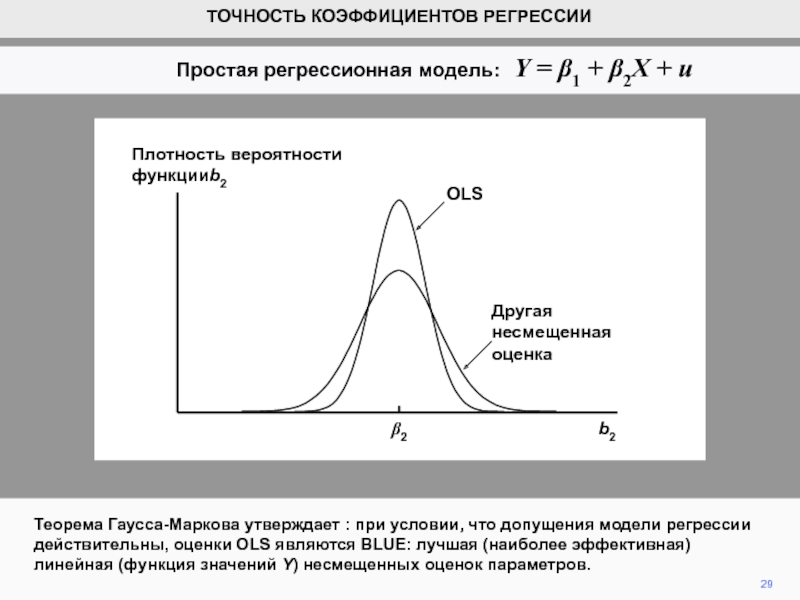
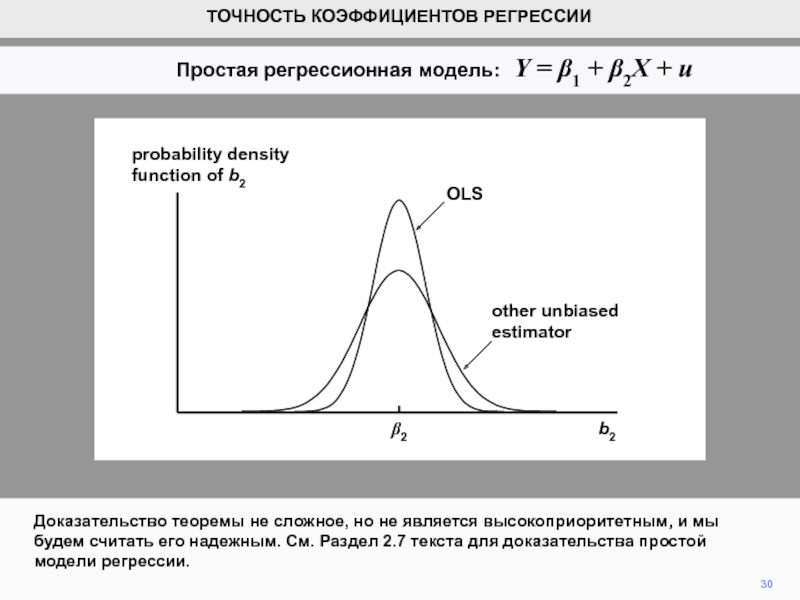
Функция плотности распределения вероятности b2
b2
b2
Стандартное отклонение плотности распределения b2