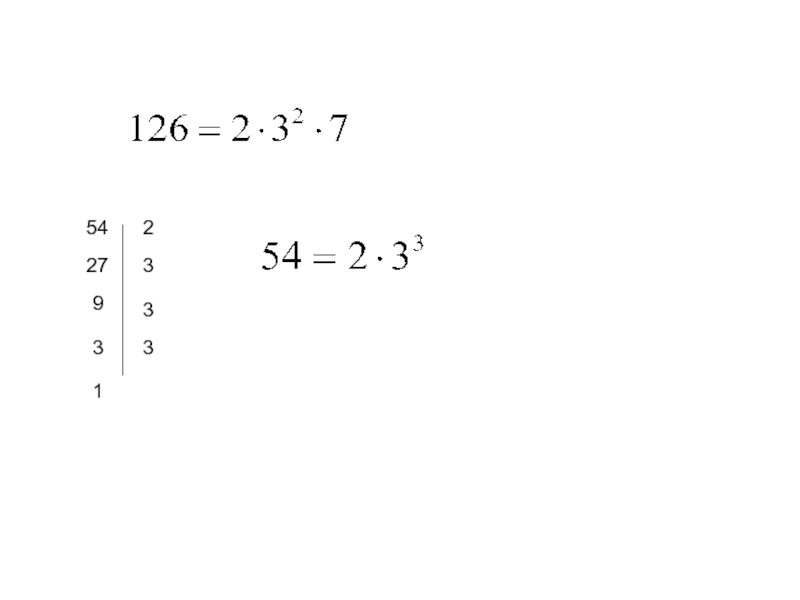Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Простые числа
Содержание
- 1. Простые числа
- 2. Определение:Простым числом называется такое натуральное число, большее
- 3. Например:Число 7 – простое.Число 2 – простое.
- 4. Классификация натуральных чиселОснование классификации - признак: быть простым числом
- 5. Свойства простых чиселСвойство1. Если простое число p
- 6. Доказательство:Предположим, что число p – простое, p≠n,
- 7. Свойство 2. Если p и g различные
- 8. Доказательство:Если p– простое число, то оно делится
- 9. Свойство 3. Если натуральное число a не
- 10. Доказательство:Пусть D(a;p)=d – наибольший общий делитель.Но p
- 11. Если d=p, то а кратно p. Это
- 12. Свойство 4. Если произведение двух натуральных чисел
- 13. Доказательство:Пусть a и p взаимно простые числа
- 14. Свойство 5. Если натуральное число больше 1,
- 15. Доказательство:Предположим противное: пусть существуют натуральные числа, большие
- 16. Если все элементы множества А есть натуральные
- 17. Число a>1, и оно либо простое, либо
- 18. b < a, ( a наименьшее число
- 19. Число а кратно b, а число b
- 20. Свойство 6. Наименьший простой делитель составного числа
- 21. Действительно: Если р наименьший простой делитель числа
- 22. Если натуральное число а, больше единицы, и
- 23. Например:Определите является ли число 137 простым.
- 24. 137 не делится на 2 137 не
- 25. Определите, какие числа простые, а какие числа составные?161, 252, 391, 837.
- 26. Эратосфен – греческий математик и астроном (III
- 27. Теорема Эвклида: Множество простых чисел бесконечно.Доказательство:Предположим противное: множество простых чисел конечно.Всякое конечное множество содержит наибольшее число.
- 28. Обозначим множество простых чисел символом М.М={2,3,5,7,11,13,…p}, где
- 29. Число а либо простое, либо составное.Но число
- 30. Основная теорема арифметики.Любое составное число можно единственным образом представить в виде произведения простых множителей
- 31. Теорема содержит два утверждения:1. Разложение на простые
- 32. Доказательство
- 33. Если-простое число, то составное число а представлено
- 34. заметим, чтоЭтот процесс конечен. Значит наступит
- 35. В полученном разложении одинаковые множители могут повторятся.Например:900=2·2·3·3·5·5
- 36. Единственность разложения составного числа на простые множителиДоказать:
- 37. Доказательство: Пусть Тогда Правая часть равенства делится наЗначит и левая часть делится на
- 38. По свойству 4 простых чисел один из
- 39. Пусть Разделив обе части равенства Имеем:И так,
- 40. Продолжая рассуждения, придем:1) при n=l к тому,
- 41. 2) при nl так же к неверному
- 42. Разложение составного числа а на простые множители
- 43. 1262633213771Значит 126 =2·3·3·7
- 44. НОК(126; 54)126 : 54=2 (ост. 18), тогдаПредставим 126 и 54 в каноническом виде.
- 45. 54227393331
- 46. НОК (126;54)=НОД (126;54)=
- 47. Спасибо за внимание!
- 48. Скачать презентанцию
Определение:Простым числом называется такое натуральное число, большее 1, которое имеет только два делителя – единицу и само это число.
Слайды и текст этой презентации
Слайд 2Определение:
Простым числом называется такое натуральное число, большее 1, которое имеет
только два делителя – единицу и само это число.
Слайд 3Например:
Число 7 – простое.
Число 2 – простое.
(единственное простое четное
число).
Числа 3,11,19, 23, 113 ... являются простыми, так как эти
числа имеют по два делителя.Число 1 ……?
Слайд 5Свойства простых чисел
Свойство1. Если простое число p делится на натуральное
число n, отличное от 1, то оно совпадает с n.
Если
p- простое, аИз того, что
Слайд 6Доказательство:
Предположим, что число p – простое, p≠n, и делится на
n. Тогда, по условию число р имеет три делителя: 1,n,p.
Следовательно число p не простое. Противоречие.Значит наше предположение не верно, а верно то, что требовалось доказать.
Слайд 7Свойство 2. Если p и g различные простые числа, то
p не делится на g.
Например: 7 и 13. 13
не делится на723 и 5. 23=5·4+3
Слайд 8Доказательство:
Если p– простое число, то оно делится на 1 и
p.
По условию g-простое число, g≠p, и g≠1.
Поэтому g
не является делителем p.Что и требовалось доказать.
Слайд 9Свойство 3. Если натуральное число a не делится на простое
число p, то a и p – взаимно простые.
Например: 25
и 7; но 25:717 и 13; но 17:13
Гипотеза : наибольший общий делитель этих чисел равен 1.
Слайд 10Доказательство:
Пусть D(a;p)=d – наибольший общий делитель.
Но p - простое число
и не может делится на d, если d≠p или d≠1
Тогда
d=p или d=1.
Слайд 11Если d=p, то а кратно p. Это противоречит условию.
Значит, d=1,
тогда числа a и p – взаимно простые числа.
Что и
требовалось доказать.
Слайд 12
Свойство 4. Если произведение двух натуральных чисел (a·b) делится на
простое число p, то хотя бы одно из них делится
на p.Например: (12·5) кратно3, так как 12 кратно 3, хотя 5 не кратно 3.
Слайд 13Доказательство:
Пусть a и p взаимно простые числа (a не кратно
p).
Тогда по свойству делимости произведения натуральных чисел, следует, что b
кратно p.Что и требовалось доказать.
Слайд 14Свойство 5. Если натуральное число больше 1, то оно имеет
хотя бы один простой делитель.
Например: 2>1 и 2=2·1
27>1 и 27=3·9
Слайд 15Доказательство:
Предположим противное: пусть существуют натуральные числа, большие 1 и не
имеющие ни одного простого делителя.
Множество таких чисел обозначим символом А.
Слайд 16Если все элементы множества А есть натуральные числа, большие 1.
Значит
во множестве А есть наименьший элемент. Обозначим его символом а.
А={а, в,с…}
Слайд 17Число a>1, и оно либо простое, либо составное.
Если a –
простое, то оно не может принадлежать множеству А по условию.
Если
a –составное, то оно имеет нату-ральный делитель, отличный от 1 и a.Назовем этот натуральный делитель b.
Слайд 18
b < a, ( a наименьшее число во множестве А).
Значит b не принадлежит множеству А, и следовательно, число b
имеет простой делитель. Пусть этот делитель - натуральное число p.
Слайд 19Число а кратно b, а число b кратно р, тогда
число а кратно p (свойство транзитивности отношения делимости)
Следовательно, число а
имеет простой делитель. Противоречие с выбором множества А.Значит, сделанное предположение не верно и чисел, больших 1, но не имеющих простых делителей не существует.
Слайд 20
Свойство 6. Наименьший простой делитель составного числа a не превосходит
Определите, является ли число 137 простым или составным.
Слайд 21Действительно: Если р наименьший простой делитель числа а, то а=р·g.
Так
как р наименьший простой делитель, то р ≤ g.
Умножим неравенство
р ≤ g на р Имеем
Слайд 22
Если натуральное число а, больше единицы, и не делится ни
на одно из простых чисел, квадрат которых не превосходит а,
то число а простое.Способ распознавания простых чисел:
Слайд 23Например:
Определите является ли число 137 простым.
121
числа, не превышающие 11Это - 2, 3, 5, 7, 11
Слайд 24137 не делится на 2
137 не делится на 3
137
не делится на 5
137 не делится на 7
137 не
делится на 11Вывод: 137 – простое число
Слайд 26Эратосфен – греческий математик и астроном (III в. до н.э.)
– способ определения простых чисел – решето Эратосфена.
Евклид – греческий
математик (около 300г. до н.э.), доказавший теорему : множество простых чисел бесконечно. Историческая справка
Слайд 27Теорема Эвклида:
Множество простых чисел бесконечно.
Доказательство:
Предположим противное: множество простых чисел
конечно.
Всякое конечное множество содержит наибольшее число.
Слайд 28Обозначим множество простых чисел символом М.
М={2,3,5,7,11,13,…p}, где p- самое большое
простое число.
Рассмотрим число а, составленное так:
а= 2·3·5·7·11·…·p+1
Слайд 29Число а либо простое, либо составное.
Но число а не может
быть простым по предположению, так как оно больше самого большого
простого числа.И не может быть составным, так как дает остаток 1 при делении на любое простое число.
Противоречие, которое доказывает, что наше предположение не верно, то есть простых чисел бесконечное множество.
Слайд 30Основная теорема арифметики.
Любое составное число можно единственным образом представить в
виде произведения простых множителей
Слайд 31Теорема содержит два утверждения:
1. Разложение на простые множители любого составного
натурального числа существует.
2. Разложение на простые множители любого составного натурального
числа единственно.
Слайд 32Доказательство
существования разложения
Пусть а составное число.
Тогда (по свойству 5 простых чисел) найдется простой делитель
такой что
где a натуральное число.
Слайд 33Если
-простое число, то составное число а представлено в виде простых
множителей
Если
- составное, то у него найдется простой делитель
(Свойство 5
простых чисел)такой, что
произведения
Слайд 34 заметим, что
Этот процесс конечен. Значит наступит момент, когда последний
множитель в разложении составного числа a будет простым числом и
будет получено разложение числа a на простые множители.
Слайд 36Единственность разложения составного числа на простые множители
Доказать: разложение составных чисел
на простые множители определено однозначно.
(два разложения составного числа на простые
множители могут отличатся друг от друга лишь порядком множителей)
Слайд 37Доказательство:
Пусть
Тогда
Правая часть равенства делится на
Значит и левая часть
делится на
Слайд 38По свойству 4 простых чисел один из множителей в левой
части равенства делится
Пусть это будет множитель
Так как p
и g простые числа, тоРазделим обе части равенства на
Получим:
Аналогично устанавливаем, что левая часть делится на
Слайд 40Продолжая рассуждения, придем:
1) при n=l к тому, что при делении
на
Все множители в левой части равенства сократятся.
Следовательно, два представления
числа a отличаются только порядком следования множителей
Слайд 412) при n
не может быть равно 1.
3) При n>l так же к
неверному равенствуСледовательно, два разложения составного числа на простые множители могут отличатся друг от друга лишь порядком множителей.
Теорема доказана.
Слайд 42Разложение составного числа а на простые множители называется каноническим представлением
натурального числа.
Задание: представьте число n=126 в каноническом виде.
