Задачи линейного программирования

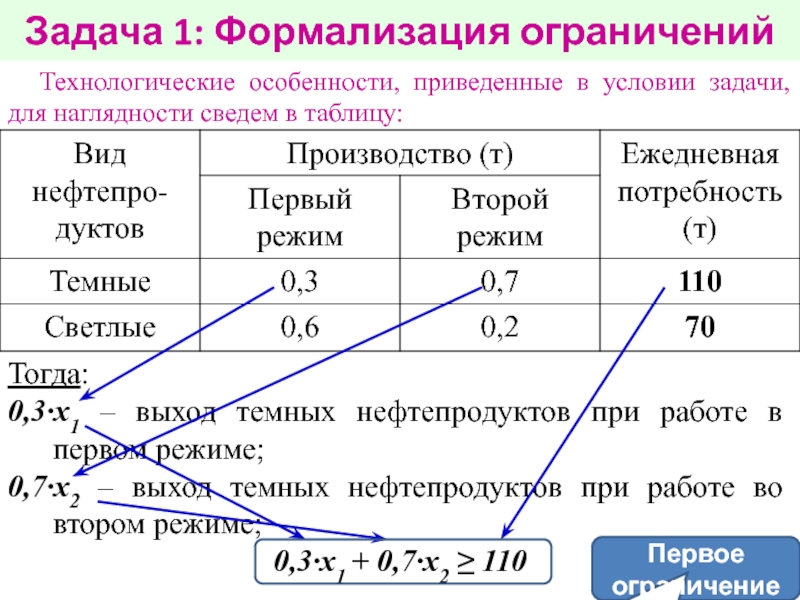
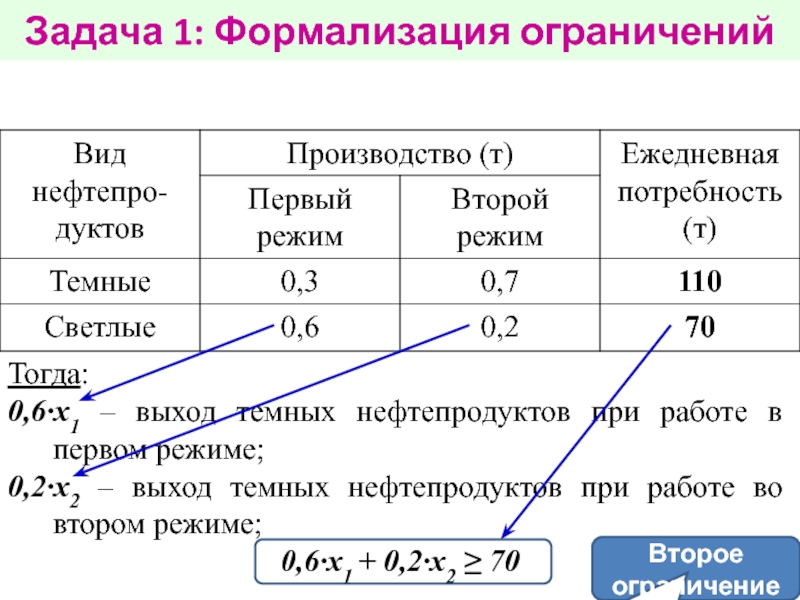
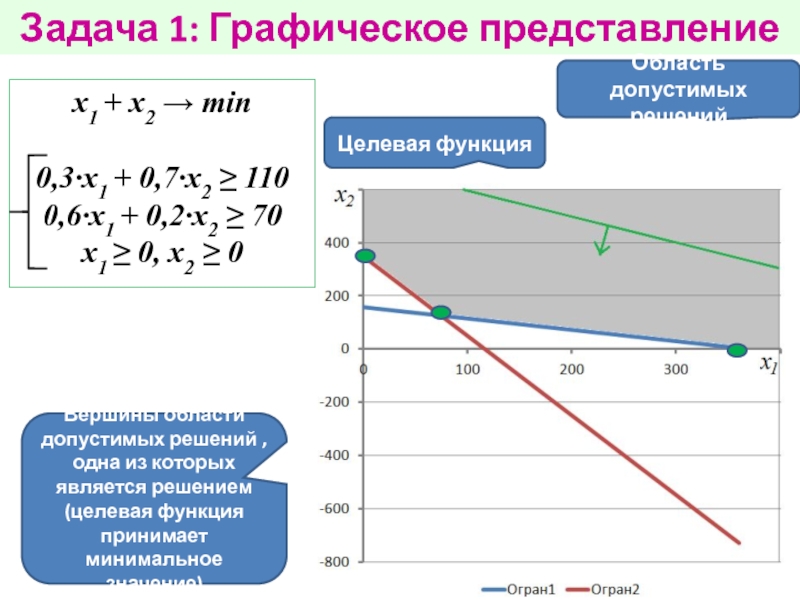
работе в первом режиме из одной тонны нефти производится 300

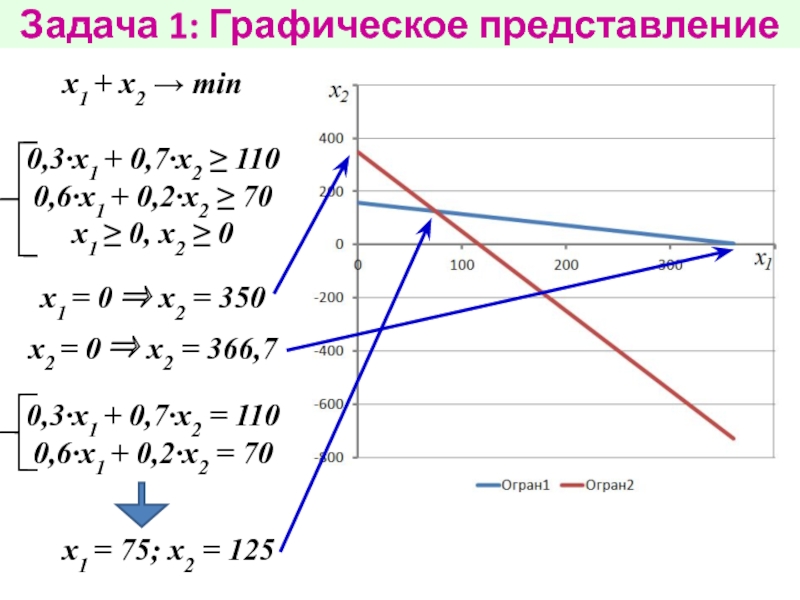
кг темных и 600 кг светлых нефтепродуктов; при работе во втором режиме — 700 кг темных и 200 кг светлых нефтепродуктов. Ежедневно на этой установке необходимо производить 110 т темных и 70 т светлых нефтепродуктов. Это плановое задание необходимо ежедневно выполнять, расходуя минимальное количество нефти.
1. Сколько тонн нефти следует ежедневно перерабатывать в первом режиме?
2. Сколько тонн нефти следует ежедневно перерабатывать во втором режиме?
3. Каков минимальный ежедневный расход нефти?
4. На сколько тонн увеличится ежедневный минимальный расход нефти, если потребуется производить в день 80 т светлых нефтепродуктов?

в первом режиме?

Пусть:
х1 – кол-во тонн нефти, перерабатываемое в первом

режиме;

2. Сколько тонн нефти следует ежедневно перерабатывать во втором режиме?

х2 – кол-во тонн нефти, перерабатываемое во втором режиме;

3. Каков минимальный ежедневный расход нефти?

Тогда:
х1 + х2 – ежедневный расход нефти (тонн).

наглядности сведем в таблицу:

Тогда:
0,3·х1 – выход темных нефтепродуктов при работе

в первом режиме;
0,7·х2 – выход темных нефтепродуктов при работе во втором режиме;
0,3·х1 + 0,7·х2 ≥ 110

Первое ограничение

в первом режиме;
0,2·х2 – выход темных нефтепродуктов при работе во

втором режиме;
0,6·х1 + 0,2·х2 ≥ 70

Второе ограничение

минимальное количество нефти
тогда:
х1 + х2 → min

0,3·х1 + 0,7·х2 ≥

110
0,6·х1 + 0,2·х2 ≥ 70
х1 ≥ 0, х2 ≥ 0

Целевая функция

Ограничения

≥ 110
0,6·х1 + 0,2·х2 ≥ 70
х1 ≥ 0, х2 ≥

0

Область допустимых решений

Целевая функция

Вершины области допустимых решений , одна из которых является решением (целевая функция принимает минимальное значение)

≥ 110
0,6·х1 + 0,2·х2 ≥ 70
х1 ≥ 0, х2 ≥

0

х1 = 0 ⇒ х2 = 350

х2 = 0 ⇒ х2 = 366,7

0,3·х1 + 0,7·х2 = 110
0,6·х1 + 0,2·х2 = 70

х1 = 75; х2 = 125

75 тонн нефти.
Во втором режиме – 125 тонн.
Минимальный ежедневный

расход нефти – 75+125 = 200 т.


4. На сколько тонн увеличится ежедневный минимальный расход нефти, если потребуется производить в день 80 т светлых нефтепродуктов?

Чтобы ответить, надо вновь строить график и решать систему уравнений

чтобы обеспечить максимальную прибыль?
2. Сколько продукта 2 следует производить для

того, чтобы обеспечить максимальную прибыль?
3. Какова максимальная прибыль?

Предприятие располагает ресурсами сырья и рабочей силы, необходимыми для производства двух видов продукции. Затраты ресурсов на изготовление одной тонны каждого продукта, прибыль, получаемая предприятием от реализации тонны продукта, а также запасы ресурсов указаны в следующей таблице:

– объём выпуска 2 продукта, т,

Тогда:
суммарная прибыль
30·х1 + 35·х2 →

max

3·х1 + 5·х2 ≤ 120
20·х1 + 12·х2 ≤ 400
x1 ≥ 0, x2 ≥ 0

Целевая функция

Ограничения

прибыль =

968,75 тыс. руб.

Множество допустимых решений

30·х1 + 35·х2 → max

3·х1 + 5·х2 ≤ 120
20·х1 + 12·х2 ≤ 400
x1 ≥ 0, x2 ≥ 0

Целевая функция

(x1, x2,…, xn), удовлетворяющих ограничениям задачи.
Оптимальное решение – это план,

при котором ЦФ принимает свое максимальное (минимальное) значение.

При описании реальной ситуации с помощью линейной модели следует проверять наличие у модели таких свойств, как пропорциональность и аддитивность.

общий объем потребления cсоответствующих ресурсов должен быть прямо пропорционален величине

этой переменной.
Например, если, продавая j-й товар в общем случае по цене 100 рублей, фирма будет делать скидку при определенном уровне закупки до уровня цены 95 рублей, то будет отсутствовать прямая пропорциональность между доходом фирмы и величиной переменной xj. Т.е. в разных ситуациях одна единица j-го товара будет приносить разный доход.

Аддитивность означает, что ЦФ и ограничения должны представлять собой сумму вкладов от различных переменных.
Примером нарушения аддитивности служит ситуация, когда увеличение сбыта одного из конкурирующих видов продукции, производимых одной фирмой, влияет на объем реализации другого.