Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
ПРОВЕРКА ГИПОТЕЗ (продолжение)
Содержание
- 1. ПРОВЕРКА ГИПОТЕЗ (продолжение)
- 2. Цели Что делать, если независимая переменная имеет больше двух уровней?
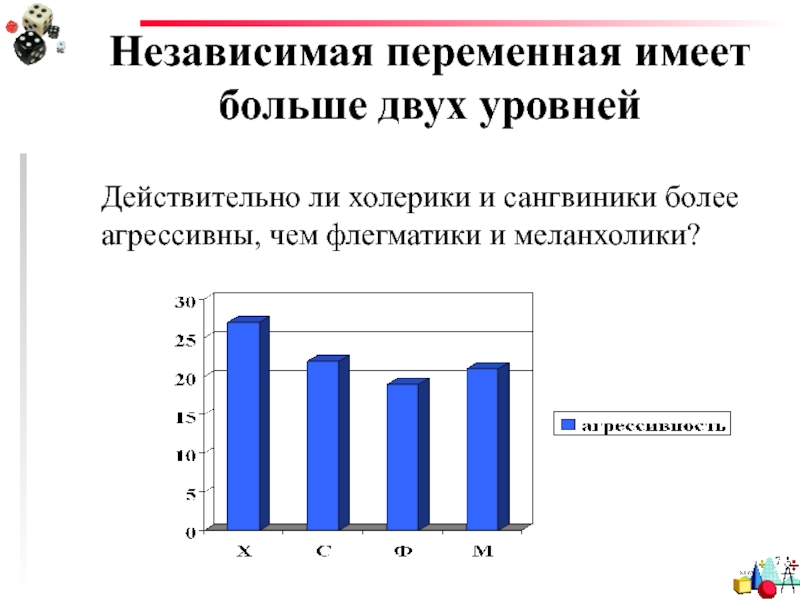
- 3. Независимая переменная имеет больше двух уровнейДействительно ли холерики и сангвиники более агрессивны, чем флегматики и меланхолики?
- 4. Независимая переменная имеет больше двух уровнейНашей задачей
- 5. Независимая переменная имеет больше двух уровней6 сравнений:Вероятность
- 6. Независимая переменная имеет больше двух уровнейВероятность не
- 7. Независимая переменная имеет больше двух уровнейДля 10
- 8. Независимая переменная имеет больше двух уровнейЧто делать?Применять специальные критерии!
- 9. Основы дисперсионного анализаВ качестве такого критерия для параметрических данных используется ДИСПЕРСИОННЫЙ АНАЛИЗ
- 10. Непараметрические аналоги ДАКритерий ФридманаКритерий Краскала-Уоллиса
- 11. Критерий Краскала-УоллисаНепараметрический аналог однофакторного ДА для независимых
- 12. Критерий Краскала-УоллисаЧем меньше совпадений, тем больше различаются ряды, соответствующие сравниваемым выборкам
- 13. Критерий Краскала-УоллисаОсновная идея критерия основана на представлении
- 14. Критерий Краскала-УоллисаЕсли выполняется статистическая гипотеза об отсутствии
- 15. Критерий Краскала-УоллисаN – общая численность всех выборокni
- 16. Критерий 2 ФридманаНепараметрический аналог однофакторного ДА для
- 17. Критерий 2 ФридманаЕсли выполняется статистическая гипотеза об
- 18. Критерий 2 Фридманаn – число испытуемыхс –
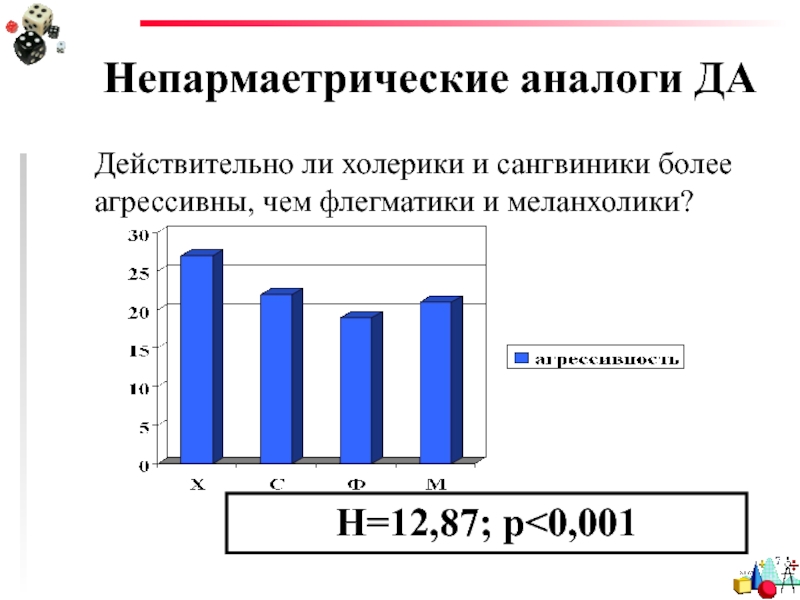
- 19. Непармаетрические аналоги ДАДействительно ли холерики и сангвиники более агрессивны, чем флегматики и меланхолики?Н=12,87; p
- 20. Непараметрические аналоги ДА
- 21. Непараметрические аналоги ДАПодсчитывать апостериорные критерии вручную по
- 22. Поправка Бонферрони Идея заключается в
- 23. Поправка Бонферрони Новый уровень статистической
- 24. Поправка Бонферрони
- 25. Поправка БонферрониОчевидно, что такой подход при достаточно
- 26. СПАСИБО ЗА ВНИМАНИЕ!
- 27. Скачать презентанцию
Цели Что делать, если независимая переменная имеет больше двух уровней?
Слайды и текст этой презентации
Слайд 3Независимая переменная имеет больше двух уровней
Действительно ли холерики и сангвиники
более агрессивны, чем флегматики и меланхолики?
Слайд 4Независимая переменная имеет больше двух уровней
Нашей задачей является избегание ошибки
I рода.
Если мы примем уровень статистической значимости равным 0,05,
мы согласимся принять риск ошибиться в 5 случаях из 100. Когда происходит много сравнений, этот риск увеличивается.Слайд 5Независимая переменная имеет больше двух уровней
6 сравнений:
Вероятность сделать ошибку при
каждом сравнении примем за 0,05.
Тогда вероятность не сделать ошибку
1-0,05=0,95.
Слайд 6Независимая переменная имеет больше двух уровней
Вероятность не сделать ошибку во
всех 6 сравнениях
(0,95)6=0,74.
А вероятность допустить ошибку хотя
бы в одном сравнении равна 1-0,74=0,26 !
Слайд 7Независимая переменная имеет больше двух уровней
Для 10 сравнений вероятность сделать
по крайней мере одну ошибку равна 0,40,
для 20 сравнений
– уже 0,64!!!Слайд 9Основы дисперсионного анализа
В качестве такого критерия для параметрических данных используется
ДИСПЕРСИОННЫЙ АНАЛИЗ
Слайд 11Критерий Краскала-Уоллиса
Непараметрический аналог однофакторного ДА для независимых выборок.
По идее сходен
с критерием Манна-Уитни: оценивает степень пересечения (совпадения) нескольких рядов значений
измеренного признака.Слайд 12Критерий Краскала-Уоллиса
Чем меньше совпадений, тем больше различаются ряды, соответствующие сравниваемым
выборкам
Слайд 13Критерий Краскала-Уоллиса
Основная идея критерия основана на представлении всех значений сравниваемых
выборок в виде одной общей последовательности упорядоченных (ранжированных) значений, с
последующим вычислением среднего ранга для каждой из выборокСлайд 14Критерий Краскала-Уоллиса
Если выполняется статистическая гипотеза об отсутствии различий, то можно
ожидать, что все средние ранги примерно равны и близки к
общему среднему рангу.Слайд 15Критерий Краскала-Уоллиса
N – общая численность всех выборок
ni – численность выборки
i
k – количество сравниваемых выборок
Ti – сумма рангов для i-й
выборкиЧем сильнее различаются выборки, тем больше вычисленное значение Н и тем меньше уровень значимости р.
Слайд 16Критерий 2 Фридмана
Непараметрический аналог однофакторного ДА для зависимых выборок.
Основан на
ранжировании ряда повторных измерений для каждого объекта выборки. Затем вычисляется
сумма рангов для каждого из условий (повторных измерений).Слайд 17Критерий 2 Фридмана
Если выполняется статистическая гипотеза об отсутствии различий между
повторными измерениями, то можно ожидать примерное равенство сумм рангов этих
условий.Чем больше различаются зависимые выборки по изучаемому признаку, тем больше эмпирическое значение 2-Фридмана
Слайд 18Критерий 2 Фридмана
n – число испытуемых
с – количество условий (повторных
измерений)
Ti – сумма рангов для условия i
Чем сильнее различаются зависимые
выборки по изучаемому признаку, тем больше эмпирическое значение 2 и тем меньше уровень значимости р.Слайд 19Непармаетрические аналоги ДА
Действительно ли холерики и сангвиники более агрессивны, чем
флегматики и меланхолики?
Н=12,87; p
Слайд 21Непараметрические аналоги ДА
Подсчитывать апостериорные критерии вручную по формулам (Радчикова Н.П.
"Компьютерная обработка психологической информации" (часть 1). Учебно-методическое пособие. – Мн.:
БГПУ, 2003)Считать соответственно критерии Манна-Уитни и Вилкоксона несколько раз с поправкой Бонферрони
Слайд 22Поправка Бонферрони
Идея заключается в том, чтобы заранее
снизить вероятность допущения ошибки I-го рода так, чтобы при выбранном
количестве сравнений вероятность не допустить хотя бы одну ошибку не превосходила, например, 0,05.Слайд 23Поправка Бонферрони
Новый уровень статистической значимости получается из
формулы:
(1-)k=0,95,
где k – число сравнений.
Слайд 24Поправка Бонферрони
Так
как
,то для 6 сравнений =0,01. Следовательно, все различия, не достигшие уровня значимости 0,01 (по критерию Манна-Уитни, например), должны будут считаться незначимыми.