TheSlide.ru

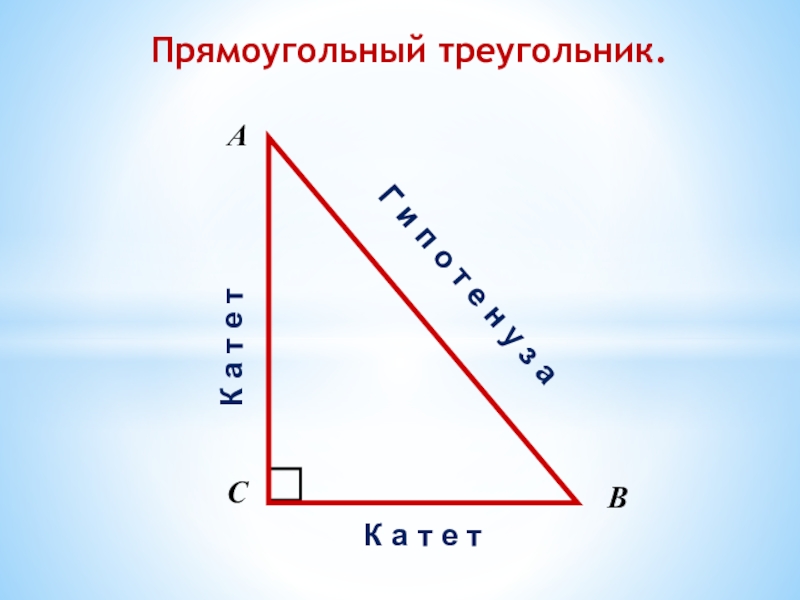
ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ

Содержание

1. ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ
2. АВСК а т е тК а т
3. Сумма двух острых углов прямоугольного треугольника равна
4. АЗадача 1.Найти: < BРешение:∆ ABC – прямоугольный<
5. Задача 2Найти острые углы прямоугольного равнобедренного треугольника.Решение:∆
6. Задача 3В прямоугольном треугольнике MNP c прямым
7. Свойство 2Катет прямоугольного треугольника, лежащий против угла
8. САВ=?РRЗадачи∆ ABC – прямоугольный < A =
9. Свойство 3Если катет прямоугольного треугольника равен половине
10. В равнобедренном треугольнике ABC (AC - основание)высота
11. Домашнее заданиеП.35 № 254, 257, 260
12. Скачать презентанцию

АВСК а т е тК а т е тГ и п о т е н у з аПрямоугольный треугольник.

Главная
Разное
ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ

Слайды и текст этой презентации

Слайд 1И НЕКОТОРЫЕ ИХ СВОЙСТВА.
ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ

И НЕКОТОРЫЕ ИХ СВОЙСТВА.ПРЯМОУГОЛЬНЫЕ ТРЕУГОЛЬНИКИ

Слайд 2А
В
С
К а т е т
К а т е т
Г и

п о т е н у з а
Прямоугольный треугольник.

АВСК а т е тК а т е тГ и п о т е н у з

Слайд 3Сумма двух острых углов прямоугольного треугольника равна 90º
Доказательство:
ΔABC – прямоугольный,

С – прямой, т.е. < C = 900
Свойство 1
A
B
C
По

теореме о сумме углов
треугольника:
A+ B + C = 180º.
Значит
A+ B = 180º - C = 90º

Сумма двух острых углов прямоугольного треугольника равна 90ºДоказательство:ΔABC – прямоугольный, С – прямой, т.е. < C

Слайд 4А
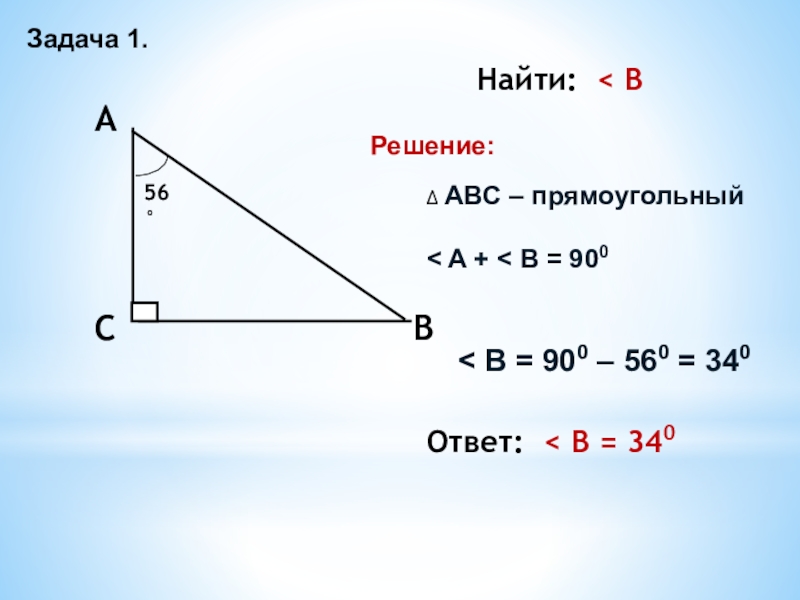
Задача 1.
Найти: < B
Решение:
∆ ABC – прямоугольный

< A +

B = 900
< B = 900 – 560 = 340
Ответ:

< B = 340

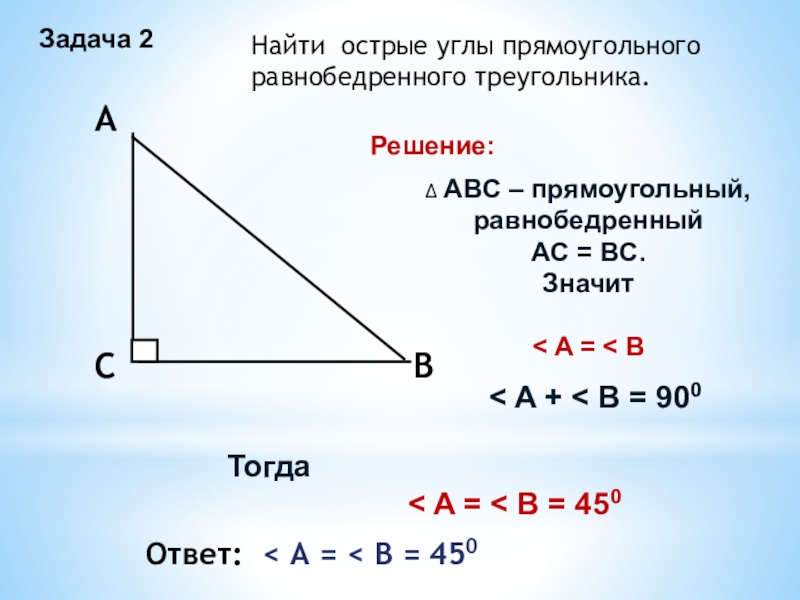
АЗадача 1.Найти: < BРешение:∆ ABC – прямоугольный< A + < B = 900< B = 900 –

Слайд 5Задача 2
Найти острые углы прямоугольного
равнобедренного треугольника.
Решение:
∆ ABC – прямоугольный,

равнобедренный
AC = BC.
Значит

< A = < B

A + < B = 900

Тогда
< A = < B = 450

Ответ: < A = < B = 450

Задача 2Найти острые углы прямоугольного равнобедренного треугольника.Решение:∆ ABC – прямоугольный, равнобедренный AC = BC. Значит < A

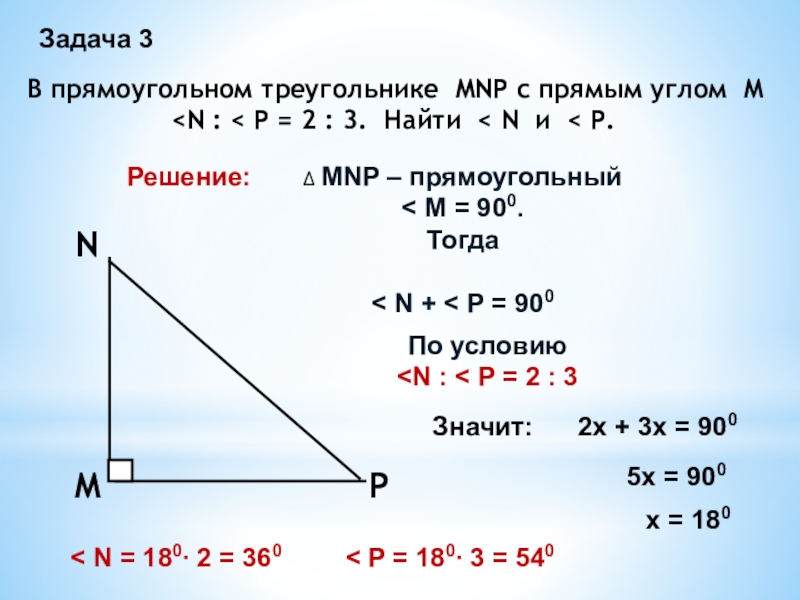
Слайд 6Задача 3
В прямоугольном треугольнике MNP c прямым углом М

< P = 2 : 3. Найти < N и < P.

Решение:

∆ MNP – прямоугольный
< M = 900.
Тогда

< N + < P = 900

По условию

Значит: 2x + 3x = 900

5x = 900

x = 180

< N = 180∙ 2 = 360

< P = 180∙ 3 = 540

Задача 3В прямоугольном треугольнике MNP c прямым углом М

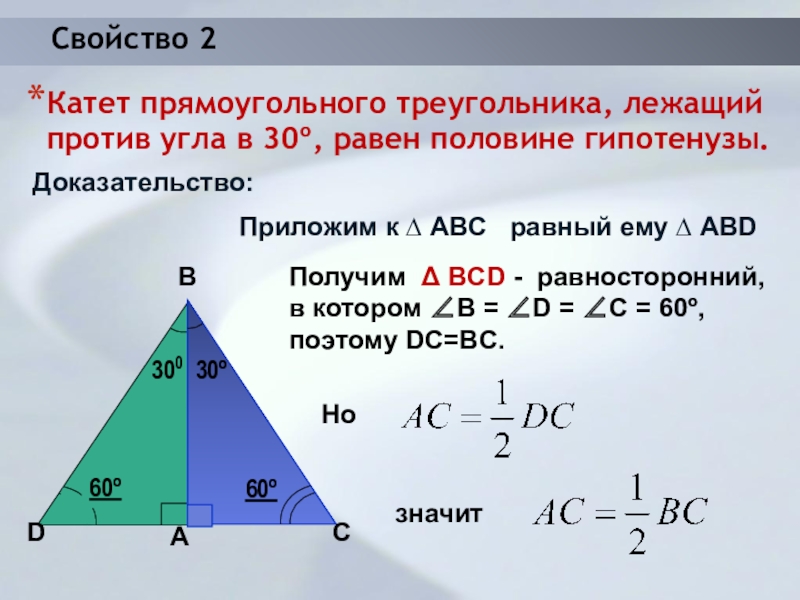
Слайд 7Свойство 2
Катет прямоугольного треугольника, лежащий против угла в 30º, равен

половине гипотенузы.
Доказательство:
Получим Δ BСD - равносторонний, в котором B =

D = С = 60º, поэтому DC=BC.

D

300

Приложим к ∆ ABC равный ему ∆ ABD

Но

значит

60º

Свойство 2Катет прямоугольного треугольника, лежащий против угла в 30º, равен половине гипотенузы.Доказательство:Получим Δ BСD - равносторонний, в

Слайд 8С
АВ=?
Р
R
Задачи
∆ ABC – прямоугольный

< A = 300 , значит

AB

= 2 BC

AB = 8 см
∆ PRS – прямоугольный

P = 300 , значит

RS = PR

RS = 8,4 : 2 = 4,2 см

1.

2.

RS=?

САВ=?РRЗадачи∆ ABC – прямоугольный < A = 300 , значитAB = 2 BCAB = 8 см∆ PRS

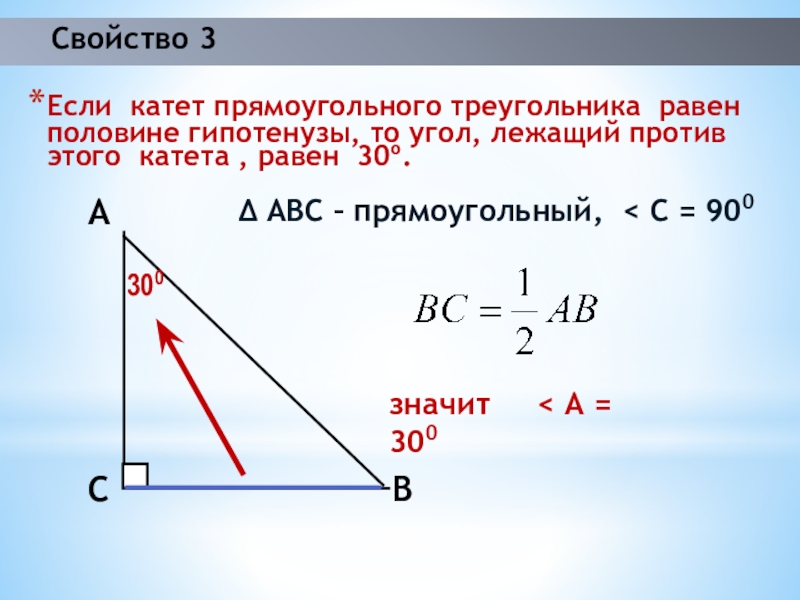
Слайд 9Свойство 3
Если катет прямоугольного треугольника равен половине гипотенузы, то угол,

лежащий против этого катета , равен 30º.
∆ ABC – прямоугольный,

< C = 900

значит < A = 300

300

Свойство 3Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета , равен 30º.∆

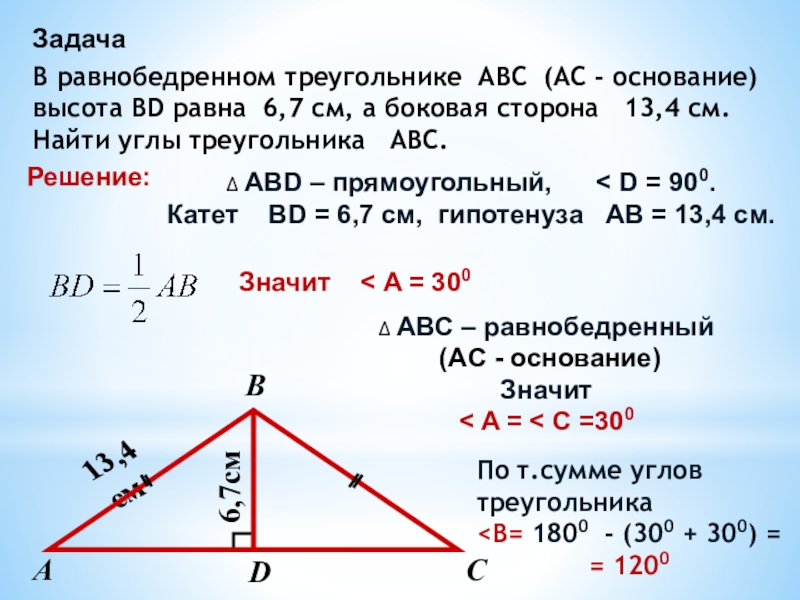
Слайд 10В равнобедренном треугольнике ABC (AC - основание)
высота BD равна 6,7

см, а боковая сторона 13,4 см.
Найти углы треугольника

ABC.

Задача

Решение:

∆ ABD – прямоугольный, < D = 900.
Катет BD = 6,7 см, гипотенуза AB = 13,4 см.

Значит < A = 300

∆ ABC – равнобедренный
(AC - основание)
Значит
< A = < C =300

По т.сумме углов
треугольника
= 1200

В равнобедренном треугольнике ABC (AC - основание)высота BD равна 6,7 см, а боковая сторона 13,4 см.Найти

Слайд 11 Домашнее задание
П.35
№ 254, 257, 260

Домашнее заданиеП.35 № 254, 257, 260

Скачать презентацию

Обратная связь

Если не удалось найти и скачать доклад-презентацию, Вы можете заказать его на нашем сайте. Мы постараемся найти нужный Вам материал и отправим по электронной почте. Не стесняйтесь обращаться к нам, если у вас возникли вопросы или пожелания:

Email: Нажмите что бы посмотреть

Что такое TheSlide.ru?

Это сайт презентации, докладов, проектов в PowerPoint. Здесь удобно хранить и делиться своими презентациями с другими пользователями.

Для правообладателей