Слайд 1КОМПЬЮТЕРНЫЕ МЕТОДЫ ОБРАБОТКИ ИНФОРМАЦИИ
Лекция 12 (С)
Компьютерное моделирование человеческих рассуждений
Слайд 2Содержание курса
«Компьютерные методы обработки информации»
Раздел 1. «Базовые методы
компьютерной обработки информации»
Принципы построения систем компьютерной обработки информации
Методы компьютерного
представления информации
Численные методы решения задач. Отыскание оптимальных решений
Раздел 2. «Методы обработки сигналов и изображений»
Случайности, шумы, искажения. Оценивание, фильтрация
Цифровые преобразования сигналов и изображений
Сравнение данных. Поиск данных
Сегментация и описание данных. Описание формы изображений
Анализ динамически меняющихся данных
Раздел 3. «Методы интеллектуального анализа данных»
Компьютерное моделирование человеческих рассуждений
Компьютерное распознавание образов и машинное обучение
Слайд 3Содержание лекции
Булева алгебра и булевы функции.
Формальные теории и исчисление
предикатов.
Логическое программирование. ПРОЛОГ
Модели представления знаний: базы фактов, фреймы и
семантические сети
Обработка символьной информации и преобразование математических выражений.
Экспертные системы.
Нечеткие логики. Байесовское объединение свидетельств. Схема Демпстера-Шафера.
Компьютерная диагностика в медицине. Анализ рентгеновских и томографических изображений.
Анализ свидетельств на изображениях.
Слайд 4Булева алгебра и булевы функции.
Формальные теории и исчисление предикатов.
Слайд 5Булева алгебра. Булевы функции
Слайд 6Булева алгебра. Булевы функции
Слайд 7Булева алгебра. Булевы функции
Слайд 8Булева алгебра. Булевы функции
Слайд 9Булева алгебра. Булевы функции
Слайд 10Булева алгебра. Равносильные формулы
Слайд 11Булева алгебра. Подстановка и замена
Слайд 12Булева алгебра. Принцип двойственности
Слайд 13Булева алгебра. Эквивалентные преобразования
Слайд 14Булева алгебра. Полнота реализации
Слайд 15Логические исчисления. Логика Аристотеля
Слайд 16Логические исчисления. Высказывания
Слайд 18Логические исчисления. Интерпретация формул
Слайд 19Логические исчисления. Логические эквивалентности
Слайд 20Логические исчисления. Подстановки
Слайд 22Формальные теории. Выводимость формул. Теоремы
Слайд 23Формальные теории. Интерпретация
Слайд 24Формальные теории.
Общезначимость и непротиворечивость
Слайд 25Формальные теории.
Полнота, независимость и разрешимость
Слайд 30Исчисление предикатов. Интерпретация
Слайд 31Исчисление предикатов. Следование и эквивалентность
Слайд 32Исчисление предикатов. Формальная арифметика
Слайд 33Ограничения: теоремы Гёделя о неполноте
Слайд 34Автоматическое доказательство теорем
Слайд 35Автоматическое доказательство теорем. Резолюции
Слайд 36Автоматическое доказательство теорем. Резолюции
Слайд 37Автоматическое доказательство теорем. Резолюции
Слайд 38Логическое программирование
Логическое программирование — парадигма программирования, основанная на автоматическом доказательстве
теорем, а также раздел дискретной математики, изучающий принципы логического вывода
информации на основе заданных фактов и правил вывода. Логическое программирование основано на теории и аппарате математической логики с использованием математических принципов резолюций.
Самым известным языком логического программирования является Prolog.
Пролог (фр. Programmation en Logique) — язык и система логического программирования, основанные на языке предикатов математической логики дизъюнктов Хорна, представляющей собой подмножество логики предикатов первого порядка.
Основными понятиями в языке Пролог являются факты, правила логического вывода и запросы, позволяющие описывать базы знаний, процедуры логического вывода и принятия решений.
Факты в языке Пролог описываются логическими предикатами с конкретными значениями. Правила в Прологе записываются в форме правил логического вывода с логическими заключениями и списком логических условий.
Пролог воспринимает в качестве программы некоторое описание задачи или баз знаний и сам производит логический вывод, а также поиск решения задач, пользуясь механизмом поиска с возвратом и унификацией.

Слайд 39ПРОЛОГ
Термы
Программа на Прологе описывает отношения, определяемые с помощью предложений.
Как и в любом другом языке, ориентированном на символьные вычисления,
предложения выстраиваются из термов, которые в свою очередь подразделяются на атомы, числа, переменные и структуры.
Атом записывается со строчной буквы или заключается в кавычки, когда требуется запись с прописной буквы.
atom 'Atom'
Переменные, записывающиеся с прописной буквы, отличаются от переменных в процедурных языках программирования, они не связаны с конкретной ячейкой памяти, а скорее ближе к математической переменной.
X is 2 + 2.
Структуры представляют собой совокупности термов, заключенные в круглые скобки, в том числе и другие структуры. Структура обозначается именем (функтором), которое располагается перед круглыми скобками.
book('Название', '2009', 'Спб', authors('Первый автор', 'Второй автор')).
Слайд 40ПРОЛОГ
Термы
Еще одной конструкцией являются списки, элементы которых заключаются в
квадратные скобки. В основе списков в Пролог лежат связанные списки.
List
= [a, b, [c, d], e].
Правила
В чистом Прологе предложения ограничиваются Дизъюнктами Хорна
Вывод :- Условие.
и читаются как: Заголовок ИСТИНА, если Тело ИСТИНА. Тело правила содержит ссылки на предикаты, которые называются целями правила. Встроенные предикаты ,/2, означающий оператор с двумя аргументами, определяющий конъюнкцию целей и ;/2 определяющий дизъюнкцию.
Факты
Предложения с пустым Телом называются Фактами. Пример факта:
Кот(Иван).
Слайд 44ПРОЛОГ
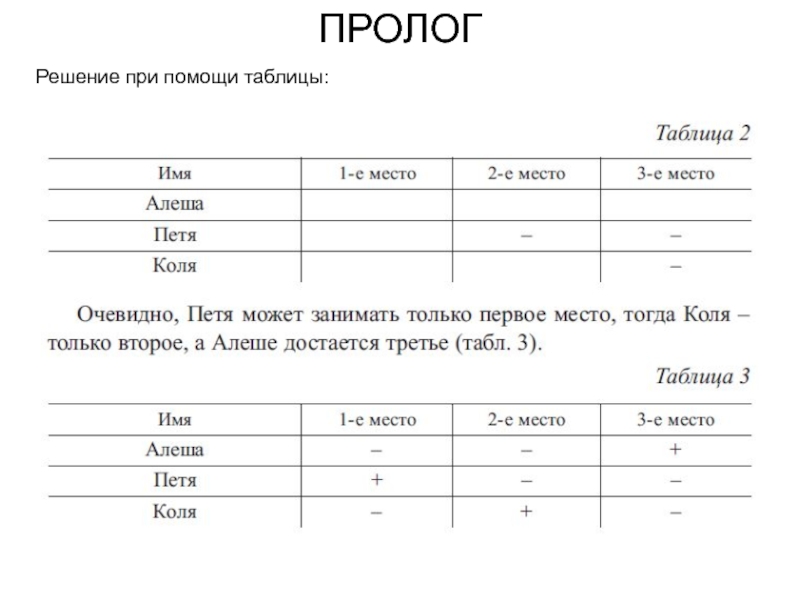
Решение при помощи таблицы:
Слайд 46ПРОЛОГ
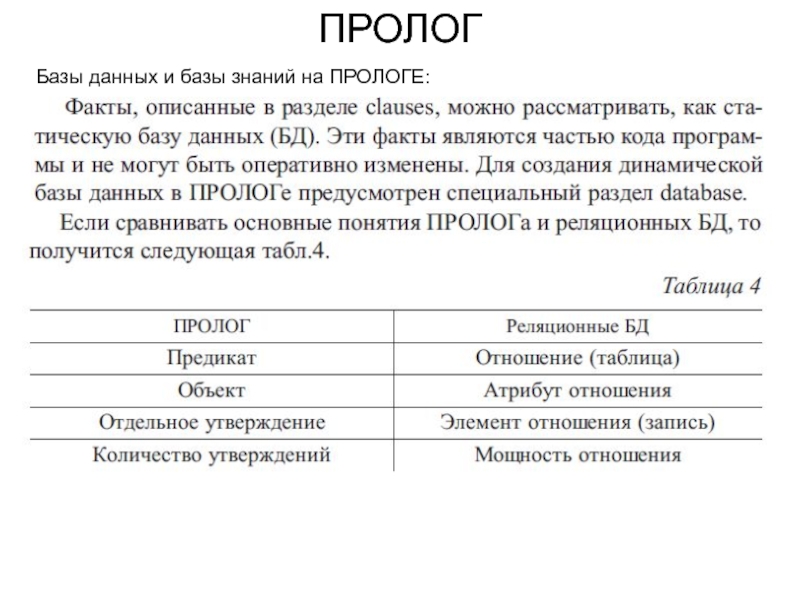
Базы данных и базы знаний на ПРОЛОГЕ:
Слайд 47ПРОЛОГ
Базы данных и базы знаний на ПРОЛОГЕ:
Слайд 48Поиск с возвратом
Поиск с возвратом (англ. Backtracking) — общий метод) — общий
метод нахождения решений задачи, в которой требуется полный перебор) — общий
метод нахождения решений задачи, в которой требуется полный перебор всех возможных вариантов в некотором множестве М. Как правило позволяет решать задачи, в которых ставятся вопросы типа: «Перечислите все возможные варианты …», «Сколько существует способов …», «Есть ли способ …», «Существует ли объект…» и т. п.
Незначительные модификации метода поиска с возвратом, связанные с представлением данных или особенностями реализации, имеют и иные названия: метод ветвей и границНезначительные модификации метода поиска с возвратом, связанные с представлением данных или особенностями реализации, имеют и иные названия: метод ветвей и границ, поиск в глубинуНезначительные модификации метода поиска с возвратом, связанные с представлением данных или особенностями реализации, имеют и иные названия: метод ветвей и границ, поиск в глубину, метод проб и ошибок и т. д.
Решение задачи методом поиска с возвратом сводится к последовательному расширению частичного решения. Если на очередном шаге такое расширение провести не удается, то возвращаются к более короткому частичному решению и продолжают поиск дальше. Данный алгоритм позволяет найти все решения поставленной задачи, если они существуют. Для ускорения метода стараются вычисления организовать таким образом, чтобы как можно раньше выявлять заведомо неподходящие варианты. Зачастую это позволяет значительно уменьшить время нахождения решения.

Слайд 49Поиск с возвратом. Пример
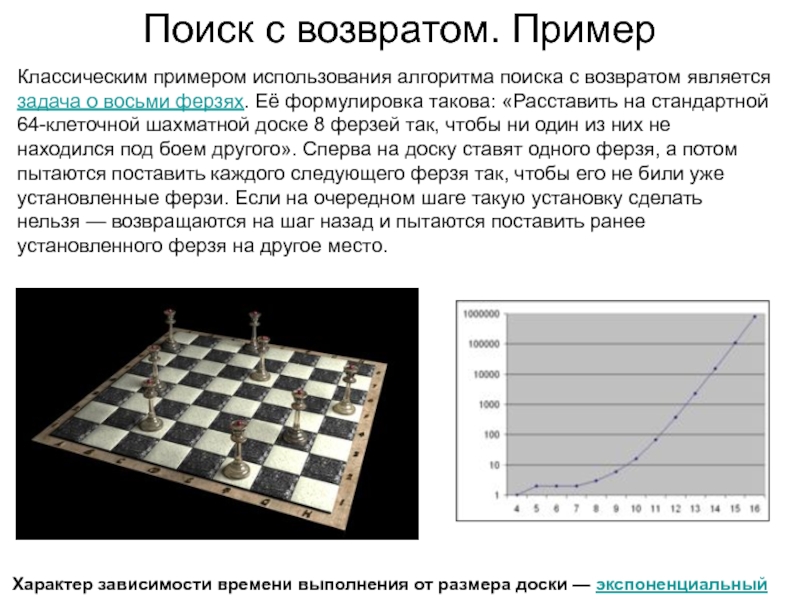
Классическим примером использования алгоритма поиска с
возвратом является задача о восьми ферзях. Её формулировка такова: «Расставить
на стандартной 64-клеточной шахматной доске 8 ферзей так, чтобы ни один из них не находился под боем другого». Сперва на доску ставят одного ферзя, а потом пытаются поставить каждого следующего ферзя так, чтобы его не били уже установленные ферзи. Если на очередном шаге такую установку сделать нельзя — возвращаются на шаг назад и пытаются поставить ранее установленного ферзя на другое место.
Характер зависимости времени выполнения от размера доски — экспоненциальный
Слайд 50Символьное программирование
Mathematica. В основе системы Mathematica лежит идея, что все
можно представить как символьное выражение. Все символьные выражения записываются в
единой форме:
Слайд 51Символьное программирование
Mathematica. В основе системы Mathematica лежит идея, что все
можно представить как символьное выражение. Все символьные выражения записываются в
единой форме:
Слайд 57Представление знаний
Представление знаний — вопрос, возникающий в когнитологии (науке о мышлении),
в информатике (науке о мышлении), в информатике и в исследованиях
искусственного интеллекта.
В когнитологии он связан с тем, как люди хранят и обрабатывают информацию. В информатике — с подбором представления конкретных и обобщённых знаний, сведений и фактов для накопления и обработки информации в ЭВМ.
Главная задача в искусственном интеллекте (ИИ) — научиться хранить знания таким образом, чтобы программы могли осмысленно обрабатывать их и достигнуть тем подобия человеческого интеллекта.
Под термином «представление знаний» чаще всего подразумеваются способы представления знаний, ориентированные на автоматическую обработку современными компьютерами, и, в частности, представления, состоящие из явных объектовПод термином «представление знаний» чаще всего подразумеваются способы представления знаний, ориентированные на автоматическую обработку современными компьютерами, и, в частности, представления, состоящие из явных объектов ('класс всех слонов', 'Клайд — индивид') и из суждений или утверждений о них ('Клайд — слон', 'все слоны серые'). Представление знаний в подобной явной форме позволяет компьютерам делать дедуктивные выводы из ранее сохранённого знания ('Клайд — серый').

Слайд 58Представление знаний
Методы и формализмы представления знаний - раздел в Компьютерной классификации
ACM:
I Вычислительные методологии
I.2 Искусственный интеллект
I.2.4 Методы и формализмы представления знаний:
фреймы
и скрипты
Модальная логика
Логика первого порядка
Реляционные системы
Языки представления
Представления (процедурные и основанные на правилах)
Семантические сети
Темпоральная логика
язык Пролог
Логическое программирование
База знаний
Экспертные системы
Когнитивное моделирование
Конвергентное управление
Слайд 59Представление знаний. Языки
Лучше всего будет представлять знания так же, как
они представлены в человеческом разуме, который является единственным известным на
сегодняшний день работающим разумом, или же представлять знания в форме естественного языка.
К сожалению, мы не умеем автоматически оперировать с естественным языком так, как это делает человек. Естественные языки формировались и формируются национальными или профессиональными сообществами людей. Знания передаются от одного человека к другому, после их перевода на язык, который понимают человек источник знания и человек приемник знания. Искусственные языки создаются для связи человека с машинами. Для представления знаний были предложены различные искусственные языки Для представления знаний были предложены различные искусственные языки и нотации Для представления знаний были предложены различные искусственные языки и нотации. Обычно они основаны на логике Для представления знаний были предложены различные искусственные языки и нотации. Обычно они основаны на логике и математике Для представления знаний были предложены различные искусственные языки и нотации. Обычно они основаны на логике и математике, и имеют легко читаемую грамматику Для представления знаний были предложены различные искусственные языки и нотации. Обычно они основаны на логике и математике, и имеют легко читаемую грамматику для облегчения машинной обработки Для представления знаний были предложены различные искусственные языки и нотации. Обычно они основаны на логике и математике, и имеют легко читаемую грамматику для облегчения машинной обработки. Обычно они попадают в широкую область онтологий.
Примеры искусственных языков которые используются преимущественно для представления знаний:
CycLCycL, IKLCycL, IKL, KIFCycL, IKL, KIF, Loom, OWL, KM : Машина Знаний (англ. Knowledge Machine) (фреймовый) (фреймовый язык, использовавшийся для задач представления знаний), язык Пролог

Слайд 60Представление знаний. Онтологии
Онтология (в информатике) — это попытка всеобъемлющей и детальной
формализации (в информатике) — это попытка всеобъемлющей и детальной формализации некоторой
области знаний (в информатике) — это попытка всеобъемлющей и детальной формализации некоторой области знаний с помощью концептуальной схемы (в информатике) — это попытка всеобъемлющей и детальной формализации некоторой области знаний с помощью концептуальной схемы. Обычно такая схема состоит из структуры данных (в информатике) — это попытка всеобъемлющей и детальной формализации некоторой области знаний с помощью концептуальной схемы. Обычно такая схема состоит из структуры данных, содержащей все релевантные (в информатике) — это попытка всеобъемлющей и детальной формализации некоторой области знаний с помощью концептуальной схемы. Обычно такая схема состоит из структуры данных, содержащей все релевантные классы объектов, их связи и правила (теоремы, ограничения), принятые в этой области.
Онтологии используются в процессеОнтологии используются в процессе программированияОнтологии используются в процессе программирования как форма представления знанийОнтологии используются в процессе программирования как форма представления знаний о реальном мире или его части. Основные сферы применения — моделирование бизнес-процессовОнтологии используются в процессе программирования как форма представления знаний о реальном мире или его части. Основные сферы применения — моделирование бизнес-процессов, искусственный интеллект.
Онтология в информатике должна иметь формат, который компьютер сможет легко обработать. Информационные онтологии создаются всегда с конкретными целями — решения конструкторских задач; они оцениваются больше с точки зрения применимости, чем полноты.
Современные онтологии строятся по большей части одинаково, независимо от языка написания. Обычно они состоят из экземпляровСовременные онтологии строятся по большей части одинаково, независимо от языка написания. Обычно они состоят из экземпляров, понятийСовременные онтологии строятся по большей части одинаково, независимо от языка написания. Обычно они состоят из экземпляров, понятий, атрибутовСовременные онтологии строятся по большей части одинаково, независимо от языка написания. Обычно они состоят из экземпляров, понятий, атрибутов и отношений.

Слайд 61Представление знаний. Онтологии
Экземпляры
Экземпляры (англ. instances) или индивиды (англ. individuals) — это основные, нижнеуровневые
компоненты онтологии. Экземпляры могут представлять собой как физические объекты (люди,
дома, планеты), так и абстрактные (числа, слова). Строго говоря, онтология может обойтись и без конкретных объектов. Однако, одной из главных целей онтологии является классификация таких объектов, поэтому они также включаются.
Понятия
Понятия (англ. concepts) (или классы (англ. classes)) — абстрактные группы, коллекции или наборы объектов. Они могут включать в себя экземпляры, другие классы, либо же сочетания и того, и другого. Пример:
Понятие «люди», вложенное понятие «человек». Чем является «человек» — вложенным понятием, или экземпляром (индивидом) — зависит от онтологии.
Понятие «индивиды», экземпляр «индивид».
Слайд 62Представление знаний. Онтологии
Атрибуты
Объекты в онтологии могут иметь атрибуты. Каждый атрибут
имеет по крайней мере имя и значение, и используется для
хранения информации, которая специфична для объекта и привязана к нему. Например, объект the Ford Explorer имеет такие атрибуты, как:
Название: Ford Explorer Число-дверей: 4 Двигатель: {4.0Л, 4.6Л}
Коробка-передач: 6-ступенчатая
Значение атрибута может быть сложным типом данных. В данном примере значение атрибута, который называется Двигатель, является списком значений простых типов данных.
Отношения
Обычно отношением является атрибут, значением которого является другой объект. Предположим, что в онтологии автомобилей присутствует два объекта — автомобиль Ford ExplorerОбычно отношением является атрибут, значением которого является другой объект. Предположим, что в онтологии автомобилей присутствует два объекта — автомобиль Ford Explorer и Ford Bronco. Пусть Bronco — это модель-наследник Explorer, тогда отношение между Ford Explorer и Ford Bronco определим как атрибут «isSuccessorOf» со значением «Explorer» для объекта Bronco.
Слайд 63Представление знаний. Онтологии
Специализированные (предметно-ориентированные) онтологии — это представление какой-либо области знаний
или части реального мира. В такой онтологии содержатся специальные для
этой области значения терминов.
Например, слово «поле» в сельском хозяйстве означает участок земли (Поле (сельское хозяйство) в сельском хозяйстве означает участок земли (Поле (сельское хозяйство)), в физике в сельском хозяйстве означает участок земли (Поле (сельское хозяйство)), в физике — один из видов материи (Поле (физика) в сельском хозяйстве означает участок земли (Поле (сельское хозяйство)), в физике — один из видов материи (Поле (физика)), в математике в сельском хозяйстве означает участок земли (Поле (сельское хозяйство)), в физике — один из видов материи (Поле (физика)), в математике — класс алгебраических систем (Поле (алгебра)).
Общие онтологии используются для представления понятий, общих для большого числа областей. Такие онтологии содержат базовый набор терминов, глоссарийОбщие онтологии используются для представления понятий, общих для большого числа областей. Такие онтологии содержат базовый набор терминов, глоссарий или тезаурус, используемый для описания терминов предметных областей.
Если использующая специализированные онтологии система развивается, то может потребоваться их объединение. Подобные онтологии часто несовместимы друг с другом, хотя могут представлять близкие области. Разница может появляться из-за особенностей местной культуры, идеологии, или вследствие использования другого языка описания. Объединение онтологий выполняют как вручную, так и в полуавтоматическом режиме. Использование базисной онтологии — единого глоссария — несколько упрощает эту работу.

Слайд 64Представление знаний. Семантические сети
Семантическая сеть — информационная модель — информационная модель предметной
области — информационная модель предметной области, имеющая вид ориентированного графа — информационная
модель предметной области, имеющая вид ориентированного графа, вершины которого соответствуют объектам предметной области, а дуги (рёбра) задают отношения между ними. Объектами могут быть понятия, события, свойства, процессы[1] — информационная модель предметной области, имеющая вид ориентированного графа, вершины которого соответствуют объектам предметной области, а дуги (рёбра) задают отношения между ними. Объектами могут быть понятия, события, свойства, процессы[1]. Таким образом, семантическая сеть является одним из способов представления знаний — информационная модель предметной области, имеющая вид ориентированного графа, вершины которого соответствуют объектам предметной области, а дуги (рёбра) задают отношения между ними. Объектами могут быть понятия, события, свойства, процессы[1]. Таким образом, семантическая сеть является одним из способов представления знаний. В названии соединены термины из двух наук: семантика — информационная модель предметной области, имеющая вид ориентированного графа, вершины которого соответствуют объектам предметной области, а дуги (рёбра) задают отношения между ними. Объектами могут быть понятия, события, свойства, процессы[1]. Таким образом, семантическая сеть является одним из способов представления знаний. В названии соединены термины из двух наук: семантика в языкознании изучает смысл единиц языка, а сеть в математике представляет собой разновидность графа — информационная модель предметной области, имеющая вид ориентированного графа, вершины которого соответствуют объектам предметной области, а дуги (рёбра) задают отношения между ними. Объектами могут быть понятия, события, свойства, процессы[1]. Таким образом, семантическая сеть является одним из способов представления знаний. В названии соединены термины из двух наук: семантика в языкознании изучает смысл единиц языка, а сеть в математике представляет собой разновидность графа — набора вершин, соединённых дугами (рёбрами). В семантической сети роль вершин выполняют понятия — информационная модель предметной области, имеющая вид ориентированного графа, вершины которого соответствуют объектам предметной области, а дуги (рёбра) задают отношения между ними. Объектами могут быть понятия, события, свойства, процессы[1]. Таким образом, семантическая сеть является одним из способов представления знаний. В названии соединены термины из двух наук: семантика в языкознании изучает смысл единиц языка, а сеть в математике представляет собой разновидность графа — набора вершин, соединённых дугами (рёбрами). В семантической сети роль вершин выполняют понятия базы знаний, а дуги (причем направленные) задают отношения между ними. Таким образом, семантическая сеть отражает семантику предметной области в виде понятий и отношений.

Слайд 65Представление знаний. Семантические сети
Основным представлением для семантической сети является граф.
Однако за ним стоит строгая математическая запись, и обе эти
формы являются не конкурирующими, а взаимодополняющими.
Графическое представление
Понятия семантической сети записываются в овалах или прямоугольниках и соединяются стрелками с подписями — дугами. Схемы семантических сетей, на которых указаны направления навигационных отношений, называют картами знаний, а их совокупность, позволяющая охватить большие участки семантической сети, атласом знания.
Математическая запись
В математике графВ математике граф представляется множеством вершин V и множеством отношений между ними E. Используя аппарат математической логики, приходим к выводу, что каждая вершина соответствует элементу предметного множества, а дуга — предикату.
Лингвистическая запись
В лингвистике отношения фиксируются в словарях и в тезаурусах. В словарях в определениях через род и видовое отличие родовое понятие занимает определённое место. В тезаурусах в статье каждого термина могут быть указаны все возможные его связи с другими родственными по теме терминами.

Слайд 66Представление знаний. Семантические сети
Классификация семантических сетей
По количеству типов отношений, сети
могут быть однородными и неоднородными.
Однородные сети обладают только одним
типом отношений (стрелок), например, таковой является классификация биологических видов.
В неоднородных сетях количество типов отношений больше двух. Неоднородные сети можно представлять как переплетение древовидных многослойных структур. Примером такой сети может быть Семантическая сеть Википедии.
По арности:
Типичными являются сети с бинарными отношениями (связывающими ровно два понятия).
На практике, однако, могут понадобиться отношения, связывающие более двух объектов — N-арные. При этом возникает сложность — как изобразить подобную связь на графе, чтобы не запутаться. Концептуальные графы снимают это затруднение, представляя каждое отношение в виде отдельного узла.
По размеру:
Для решения конкретных задач, например, тех которые решают системы искусственного интеллекта.
Семантическая сеть отраслевого масштаба должна служить базой для создания конкретных систем, не претендуя на всеобщее значение.
Глобальная семантическая сеть. Теоретически такая сеть должна существовать, поскольку всё в мире взаимосвязано. Возможно когда-нибудь такой сетью станет Всемирная паутина.

Слайд 67Представление знаний. Семантические сети
Иерархические отношения
Отношение между объектом и множеством, обозначающим,
что объект принадлежит этому множеству, называется отношением классификации (ISA). Говорят,
что множество (класс) классифицирует свои экземпляры. (пример: «Шарик является собакой» = Шарик является объектом типа собака). Связь ISA предполагает, что свойства объекта наследуются от множества. Обратное к ISA отношение используется для обозначения примеров, поэтому так и называется — «Example», или по-русски «Пример». Иерархические отношения образуют древовидную структуру.
Отношение между надмножеством и подмножеством (называется AKO — «A Kind Of», «разновидность»). (Пример: «собака является животным» = тип с именем собака является подтипом типа животные). Элемент подмножества называется гипонимом (собака), а надмножества — гиперонимом (животное), а само отношение называется отношением гипонимии (подмножество). Это отношение определяет, что каждый элемент первого множества входит и во второе (выполняется ISA для каждого элемента), а также логическую связь между самими подмножествами: что первое не больше второго и свойства первого множества наследуются вторым. Отношение АКО (Род-Вид) часто используется для навигации в информационном пространстве.

Слайд 68Представление знаний. Семантические сети
Иерархические отношения
Объект, как правило, состоит из нескольких
частей, или элементов. Например, компьютер состоит из системного блока, монитора,
клавиатуры, мыши и т. д. Важным отношением является HasPart, описывающее связь частей и целого — отношение меронимии. В этом случае свойства первого множества не наследуются вторым.
Мероним и холоним — противоположные понятия:
Мероним — объект, являющийся частью для другого. (Двигатель — мероним автомобиля.)
Холоним — объект, который включает в себя другое. (Например, у дома есть крыша. Дом — холоним крыши. Компьютер — холоним монитора.)
Семантическая сеть, упорядоченная отношениями «целое — часть», «род — вид»
Слайд 69Представление знаний. Семантические сети
Другие отношения
функциональные связи (определяемые обычно глаголами «производит»,
«влияет»…);
количественные (больше меньше, равно…);
пространственные (далеко от, близко от,
за, под, над…);
временные (раньше, позже, в течение…);
атрибутивные (иметь свойство, иметь значение);
логические (И, ИЛИ, НЕ);
лингвистические…
Семантическая паутина
Концепция организации гипертекста напоминает однородную бинарную семантическую сеть, однако здесь есть существенное отличие:
Связь, осуществляемая гиперссылкой, не имеет семантики, т. е. не описывает смысла этой связи. Назначение семантической сети состоит в том, чтобы описать взаимосвязи объектов, а не дополнительную информацию. Страницы, связываемые гиперссылками, являются документами, описывающими, как правило, проблемную ситуацию в целом. В семантической сети вершины представляют собой понятия или объекты реального мира.
Попытка создания семантической сети на основе Всемирной паутины получила название семантической паутины. Это позволит превратить Интернет. Это позволит превратить Интернет в распределённую базу знаний глобального масштаба.

Слайд 70Представление знаний. Фреймы
Фрейм — (англ. frame — «каркас» или «рамка») — способ представления
знаний в искусственном интеллекте, представляющий собой схему действий в реальной
ситуации.
Фрейм — это модель абстрактного образа, минимально возможное описание сущности какого-либо объекта, явления, события, ситуации, процесса.
Типы фреймов
Различают фреймы-образцы, фреймы-экземпляры, фреймы-структуры, фреймы-роли, фреймы-сценарии, фреймы-ситуации.
Система связанных фреймов может образовывать семантическую сеть.
Структура фрейма
Фрейм состоит из имени и отдельных единиц, называемых слотами:
ИМЯ ФРЕЙМА
Имя 1-го слота: значение 1-го слота
Имя 2-го слота: значение 2-го слота
....................................
Имя N-го слота: значение N-го слота.
В качестве значения слота может выступать имя другого фрейма.
Таким образом фреймы объединяются в сеть.
Слайд 71Представление знаний. Фреймы
Свойства фреймов
Свойства фреймов наследуются сверху вниз, т.е. от
вышестоящих к нижестоящим через так называемые АКО-связи. Слот с именем
АКО указывает на имя фрейма более высокого уровня иерархии.
Незаполненный фрейм называется протофреймом, а заполненный — экзофреймом. Роль протофрейма как оболочки в экзофрейме весьма важна. Эта оболочка позволяет осуществлять процедуру внутренней интерпретации, благодаря которой данные в памяти системы не безлики, а имеют вполне определенный, известный системе смысл.
Слот может содержать не только конкретное значение, но и имя процедурыСлот может содержать не только конкретное значение, но и имя процедуры, позволяющей вычислить его по заданному алгоритмуСлот может содержать не только конкретное значение, но и имя процедуры, позволяющей вычислить его по заданному алгоритму, а также одну или несколько продукций (эвристик), с помощью которых это значение определяется. В слот может входить не одно, а несколько значений. Иногда этот слот включает компонент, называемый фасетом, который задает диапазон или перечень его возможных значений. Фасет указывает также граничные значения заполнителя слота.

Слайд 72Представление знаний. Фреймы
Свойства фреймов
Помимо конкретного значения в слоте могут храниться
процедуры и правила, которые вызываются при необходимости вычисления этого значения.
Среди них выделяют процедуры-демоны и процедуры-слуги. Первые запускаются автоматически при выполнении некоторого условия, а вторые активизируются только по специальному запросу. Если, например, фрейм, описывающий человека, включает слоты ДАТА РОЖДЕНИЯ и ВОЗРАСТ и в первом из них находится некоторое значение, то во втором слоте может стоять имя процедуры-демона, вычисляющей возраст по дате рождения и текущей дате и активизирующейся при каждом изменении текущей даты.
Совокупность фреймов, моделирующая какую-либо предметную область, представляет собой иерархическую структуру, в которую фреймы собираются с помощью родовидовых связей. На верхнем уровне иерархии находится фрейм, содержащий наиболее общую информацию, истинную для всех остальных фреймов. Фреймы обладают способностью наследовать значения характеристик своих родителей, находящихся на более высоком уровне иерархии. Эти значения могут передаваться по умолчанию фреймам, находящимся ниже них в иерархии, но если последние содержат собственные значения данных характеристик, то в качестве истинных принимаются именно они. Это обстоятельство позволяет без затруднений учитывать во фреймовых системах различного рода исключения.

Слайд 73Представление знаний. Фреймы
Свойства фреймов
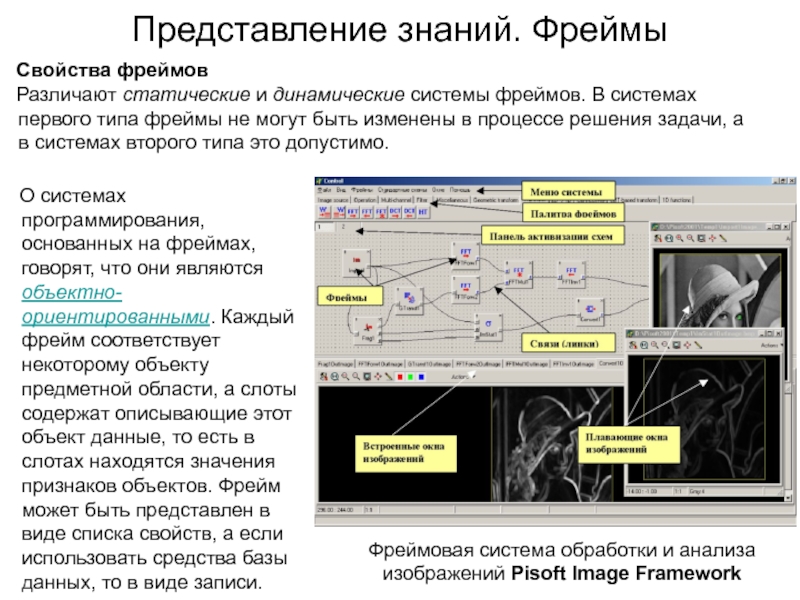
Различают
статические и динамические системы фреймов. В системах первого типа фреймы
не могут быть изменены в процессе решения задачи, а в системах второго типа это допустимо.
Фреймовая система обработки и анализа изображений Pisoft Image Framework
О системах программирования, основанных на фреймах, говорят, что они являются объектно-ориентированными. Каждый фрейм соответствует некоторому объекту предметной области, а слоты содержат описывающие этот объект данные, то есть в слотах находятся значения признаков объектов. Фрейм может быть представлен в виде списка свойств, а если использовать средства базы данных, то в виде записи.
Слайд 74Экспертные системы
Экспертная система (ЭС) — компьютерная программа, способная частично заменить специалиста-эксперта
в разрешении проблемной ситуации.
ЭС рассматриваются совместно с базами знанийЭС
рассматриваются совместно с базами знаний как модели поведения экспертовЭС рассматриваются совместно с базами знаний как модели поведения экспертов в определенной области знаний с использованием процедур логического вывода и принятия решений, а базы знаний — как совокупность фактов и правил логического вывода в выбранной предметной области деятельности.
Элементы ЭС:
Интерфейс пользователя - Пользователь -
Интеллектуальный редактор базы знаний - Эксперт -
Инженер по знаниям - Рабочая (оперативная) память - База знаний -
Решатель (механизм вывода) - Подсистема объяснений
База знанийБаза знаний состоит из правил анализа информации от пользователя по конкретной проблеме. ЭС анализирует ситуацию и, в зависимости от направленности ЭС, дает рекомендации по разрешению проблемы.
Как правило, база знаний экспертной системы содержит фактыКак правило, база знаний экспертной системы содержит факты (статические сведения о предметной области) и правила — набор инструкций, применяя которые к известным фактам можно получать новые факты.

Слайд 75Экспертные системы
База знаний ЭС создается при помощи трех групп людей:
эксперты
той проблемной области, к которой относятся задачи, решаемые ЭС;
инженеры
по знаниям, являющиеся специалистами по разработке ИИС;
программисты, осуществляющие реализацию ЭС.
ЭС может функционировать в 2-х режимах.
Режим ввода знаний — в этом режиме эксперт с помощью инженера по знаниям посредством редактора базы знаний вводит известные ему сведения о предметной области в базу знаний ЭС.
Режим консультации — пользователь ведет диалог с ЭС, сообщая ей сведения о текущей задаче и получая рекомендации ЭС. Например, на основе сведений о физическом состоянии больного ЭС ставит диагноз в виде перечня заболеваний, наиболее вероятных при данных симптомах.
Слайд 76Экспертные системы
Этапы разработки ЭС
Этап идентификации проблем — определяются задачи, которые подлежат
решению, выявляются цели разработки, определяются эксперты и типы пользователей.
Этап
извлечения знаний — проводится содержательный анализ проблемной области, выявляются используемые понятия и их взаимосвязи, определяются методы решения задач.
Этап структурирования знаний — выбираются ИС и определяются способы представления всех видов знаний, формализуются основные понятия, определяются способы интерпретации знаний, моделируется работа системы, оценивается адекватность целям системы зафиксированных понятий, методов решений, средств представления и манипулирования знаниями.
Этап формализации — осуществляется наполнение экспертом базы знаний. В связи с тем, что основой ЭС являются знания, данный этап является наиболее важным и наиболее трудоемким этапом разработки ЭС. Процесс приобретения знаний разделяют на извлечение знаний из эксперта, организацию знаний, обеспечивающую эффективную работу системы, и представление знаний в виде, понятном ЭС. Процесс приобретения знаний осуществляется инженером по знаниям на основе анализа деятельности эксперта по решению реальных задач.
Реализация ЭС — создается один или несколько прототипов ЭС, решающие требуемые задачи.
Этап тестирования — производится оценка выбранного способа представления знаний в ЭС в целом.

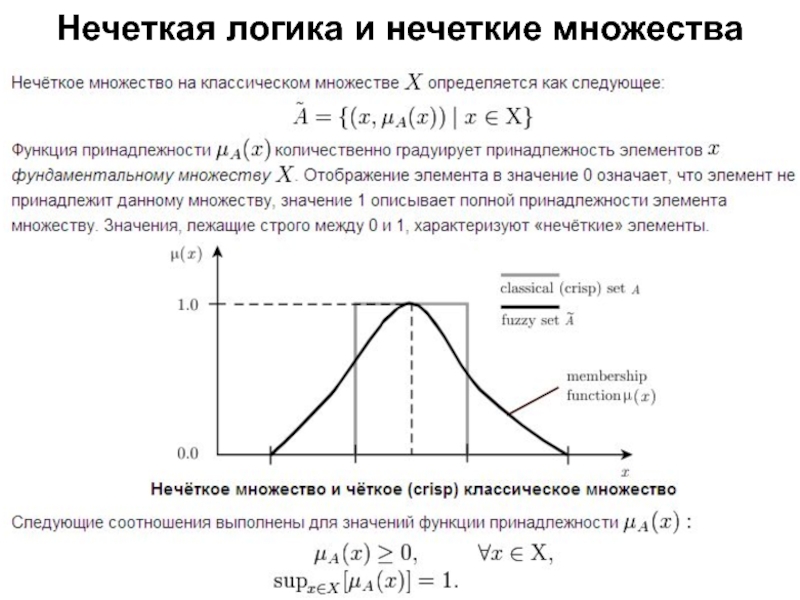
Слайд 77Нечеткая логика и нечеткие множества
Предметом нечёткой логики является построение
моделей приближенных рассуждений человека и использование их в компьютерных системах.
Нечёткая
логика и теория нечётких множеств и теория нечётких множеств — раздел математики, являющийся обобщением классической логики и теория нечётких множеств — раздел математики, являющийся обобщением классической логики и теории множеств.
Понятие нечёткой логики было впервые введено профессором Лютфи Заде в 1965 году. Понятие множества было расширено допущением, что функция принадлежности элемента к множеству может принимать любые значения в интервале [0...1], а не только 0 или 1. Такие множества были названы нечёткими. Также автором были предложены различные логические операции над нечёткими множествами и предложено понятие лингвистической переменной, в качестве значений которой выступают нечёткие множества.
Слайд 78Нечеткая логика и нечеткие множества
Слайд 79Нечеткая логика и нечеткие множества
Слайд 80Нечеткая логика и нечеткие множества
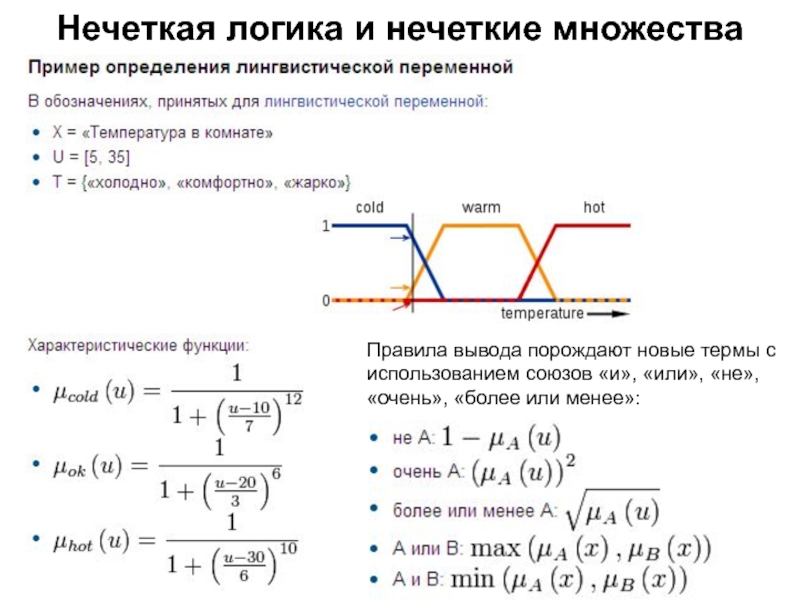
Правила вывода порождают новые термы
с использованием союзов «и», «или», «не», «очень», «более или менее»:
Слайд 81Вероятностная логика и вероятностный вывод
Вероятностная логика — логика — логика, в
которой высказываниям — логика, в которой высказываниям приписываются не исключительно значения
истины — логика, в которой высказываниям приписываются не исключительно значения истины и лжи — логика, в которой высказываниям приписываются не исключительно значения истины и лжи как в двузначной логике — логика, в которой высказываниям приписываются не исключительно значения истины и лжи как в двузначной логике, но непрерывная шкала значений истинности от 0 до 1, так что, нуль соответствует невозможному — логика, в которой высказываниям приписываются не исключительно значения истины и лжи как в двузначной логике, но непрерывная шкала значений истинности от 0 до 1, так что, нуль соответствует невозможному событию, единица — практически достоверному.
Значения истинности в вероятностной логике называются вероятностями истинности высказываний.
Байесовская сеть (или Байесова сеть,Байесовская сеть доверия) — это вероятностная модель) — это вероятностная модель, представляющая собой множество переменных) — это вероятностная модель, представляющая собой множество переменных и их вероятностных зависимостей) — это вероятностная модель, представляющая собой множество переменных и их вероятностных зависимостей. Байесовская сеть — это направленный ациклический граф, каждой вершине которого соответствует случайная переменная, а дуги графа кодируют отношения условной независимости между этими переменными.
Вероятностный вывод
В силу того, что Байесовская сеть — это полная модель для переменных и их отношений, она может быть использована для того, чтобы давать ответы на вероятностные вопросы. Например, сеть можно использовать чтобы получить новое знание о состоянии подмножества переменных наблюдая за другими переменными (переменные — свидетельства). Это процесс вычисления апостериорного распределения переменных по переменным-свидетельствам называют вероятностным выводом.

Слайд 82Байесовская схема объединения свидетельств
Слайд 83Байесовская сеть
Вероятностные запросы
Байесовская сеть позволяет получить ответы на следующие
типы вероятностных запросов:
нахождение вероятности свидетельства,
определение априорных маргинальных вероятностей,
определение
апостериорных маргинальных вероятностей, включая:
прогнозирование, или прямой вывод, — определение вероятности события при наблюдаемых причинах,
диагностирование, или обратный вывод (абдукция), — определение вероятности причины при наблюдаемых следствиях,
межпричинный (смешанный) вывод (intercausal inference) или трансдукция, — определение вероятности одной из причин наступившего события при условии наступления одной или нескольких других причин этого события.
вычисление наиболее вероятного объяснения наблюдаемого события (Most probable explanation, MPE),
вычисление апостериорного максимума (Maximum a-posteriori, MAP).
Слайд 84Байесовская сеть. Пример вывода
Предположим, что может быть две причины,
по которым трава может стать мокрой (GRASS WET): сработала дождевальная
установка, либо прошел дождь. Также предположим, что дождь влияет на работу дождевальной машины (во время дождя установка не включается). Тогда ситуация может быть смоделирована проиллюстрированной Байесовской сетью. Все три переменные могут принимать два возможных значения:
T (правда — true) и F (ложь — false).
Совместная вероятность функции:
где имена трех переменных означают
G = Трава мокрая (Grass wet),
S = Дождевальная установка (Sprinkler), R = Дождь (Rain).
Модель может ответить на такие вопросы как «Какова вероятность того, что прошел дождь, если трава мокрая?» используя формулу условной вероятности и суммируя переменные:
Слайд 85Теория Демпстера-Шафера
Теория Демпстера-Шафера— математическая теория очевидностей (свидетельств), основанная на
функции доверия (belief functions) и функции правдоподобия (plausible reasoning), которые
используются, чтобы скомбинировать отдельные части информации (свидетельства) для вычисления вероятности события. Теория была развита Артуром П. Демпстером (Arthur P. Dempster) и Гленном Шафером (Glenn Shafer).
Мотивировка: учет субъективной уверенности. Пример: игры
Первая игра — подбрасывание монеты, где ставки делаются на то, выпадет орел или решка. Теперь представим вторую игру, в которой ставки принимаются на исход боя между лучшим в мире боксером и лучшим в мире борцом. Предположим, мы несведущи в боевых искусствах, и нам весьма трудно определиться на кого ставить.
Многие люди будут менее уверены в ситуации второй игры, в которой вероятности неизвестны, чем в первой игре, где легко увидеть, что вероятность каждого исхода равна половине. В случае второй игры, Байесовская теория присвоит каждому исходу половинную вероятность, вне зависимости от информации, делающей один из исходов более вероятным, чем другой. Теория Демпстера-Шафера позволяет определить степень уверенности, которую имеет игрок, относительно вероятностей присвоенных различным исходам.

Слайд 88Схема объединения свидетельств ДШ
ДШ подход позволяет интерпретировать доверие и
правдоподобие как границы интервала возможного значения истинности гипотезы:
доверие ≤ какая-то
мера истинности ≤ правдоподобие.
Доверие к гипотезе = {сумма масс свидетельств, однозначно поддерживающих гипотезу}.
Правдоподобие = 1 − {сумма масс всех свидетельств, противоречащих гипотезе}.
Слайд 89Метод анализа свидетельств на изображениях
предназначен для обнаружения объектов заданных
типов
строится экспертная вероятностная модель, описывающая связь между особенностями изображения
(характерными чертами) и гипотезой о принадлежности объекта заданной яркостно-геометрической модели
вероятностная модель используется непосредственно в ходе низкоуровневого анализа изображения
каждая обнаруженная особенность изображения (ХЧ) рассматривается как событие, свидетельствующее в пользу гипотезы (ряда гипотез) о наличии и характеристиках искомого объекта (голосование в специальном аккумуляторном пространстве).
Способы повышения вычислительной эффективности.
независимое аккумулирование свидетельств
декомпозиция вектора параметров модели регистрации S(θ)=S'(θ')∙S"(θ")
редукция вектора параметров модели регистрации S(θ)→S'(θ')
загрубление модели объекта
M → M'⊇M
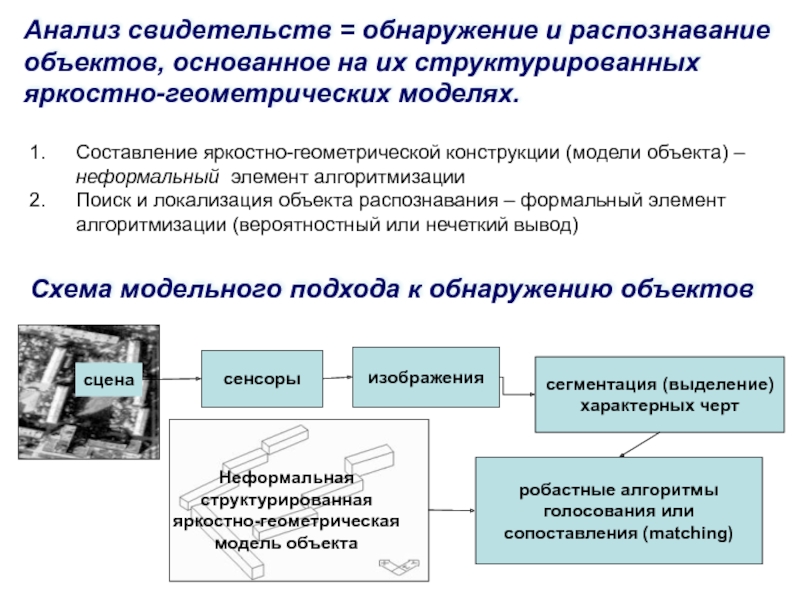
Слайд 90Анализ свидетельств = обнаружение и распознавание объектов, основанное на их
структурированных яркостно-геометрических моделях.
Составление яркостно-геометрической конструкции (модели объекта) – неформальный элемент
алгоритмизации
Поиск и локализация объекта распознавания – формальный элемент алгоритмизации (вероятностный или нечеткий вывод)
Схема модельного подхода к обнаружению объектов
робастные алгоритмы
голосования или
сопоставления (matching)
сцена
сенсоры
изображения
сегментация (выделение)
характерных черт
Неформальная
структурированная
яркостно-геометрическая
модель объекта
Слайд 91ХЧ
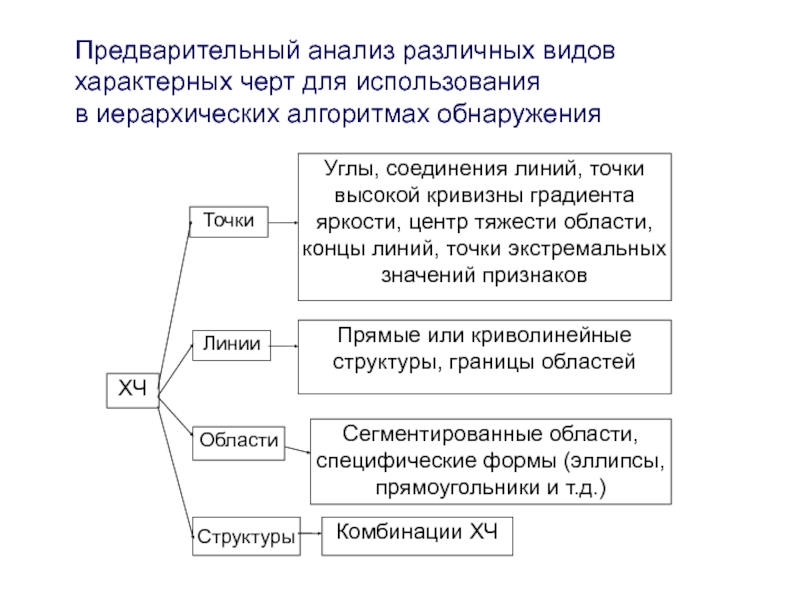
Точки
Углы, соединения линий, точки высокой кривизны градиента яркости, центр тяжести
области, концы линий, точки экстремальных значений признаков
Линии
Прямые или криволинейные структуры,
границы областей
Области
Сегментированные области, специфические формы (эллипсы, прямоугольники и т.д.)
Структуры
Комбинации ХЧ
Предварительный анализ различных видов характерных черт для использования
в иерархических алгоритмах обнаружения
Слайд 92Характерные черты на изображении имеют следующие виды атрибутов:
Положение: Концы отрезка,
центр отрезка, центр тяжести области, вершины многоугольников;
Геометрические атрибуты: Ориентация, длина,
кривизна, площадь, периметр, ширина линии, минимальный и максимальный диаметр области, оси симметрии, число и положение особых точек, показатель компактности;
Радиометрические атрибуты: Контраст, статистика распределения яркости, знак и величина края, автокорреляция;
Текстурные атрибуты: Матрица смежности, показатель однородности, энергия, энтропия, статистика градиентов текстуры, результаты применения текстурных фильтров, моменты;
Топологические атрибуты: Связность, соседство, общие точки, пересечение, параллельность, перекрытие, включение;
Цветовые/многозональные атрибуты: вектор атрибутов для каждого канала;
Динамические атрибуты: атрибуты статических и движущихся объектов;
Временные атрибуты: функции изменения атрибутов со временем.
Используемые свойства (атрибуты) характерных черт
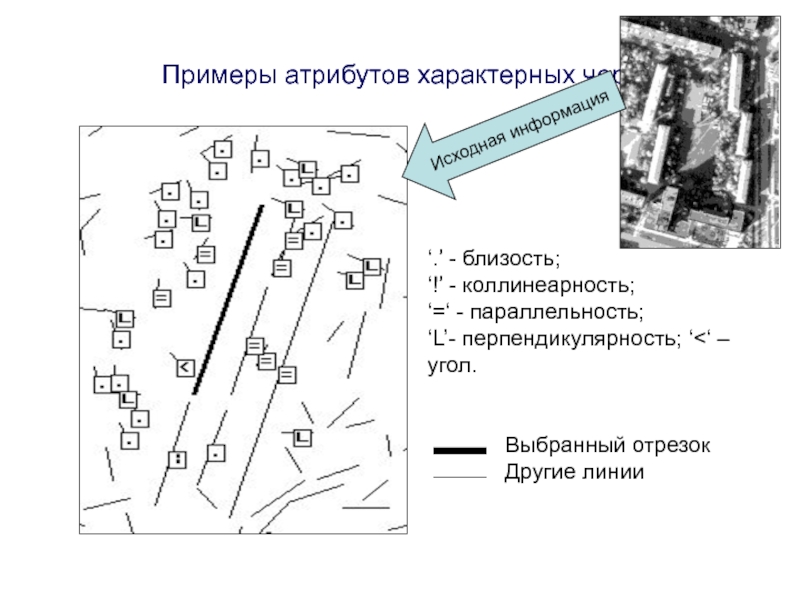
Слайд 93Примеры атрибутов характерных черт
‘.’ - близость;
‘!’ - коллинеарность;
‘=‘ - параллельность;
‘L’-
перпендикулярность; ‘
Слайд 94Присутствие/плотность: наличие данных ХЧ на всех используемых изображениях, достаточная плотность
ХЧ для покрытия интересующего района;
Редкость/Уникальность: редкость конкретной ХЧ на изображении,
уникальность ХЧ в окрестности;
Инвариантность/Устойчивость: робастность по отношению к геометрическим и радиометрическим искажениям, нечувствительность к шуму;
Локализация: возможность точной локализации;
Интерпретация: возможность быстрого распознавания и интерпретации;
Скорость: время выделения данного класса ХЧ из исходного изображения.
Выбор конкретных ХЧ и их атрибутов для построения алгоритмов обнаружения основывается на следующих критериях:
Слайд 95Пример автоматического обнаружения зданий с летательного аппарата
исходное изображение
Слайд 96Пример автоматического обнаружения зданий с летательного аппарата
Контурный препарат
Слайд 97Пример автоматического обнаружения зданий с летательного аппарата
Выделение характерных черт -
областей поддержки линеаментов
Слайд 98Пример автоматического обнаружения зданий с летательного аппарата
Выделение первичных линеаментов
Слайд 99Пример автоматического обнаружения зданий с летательного аппарата
Выделение крупных и/или параллельных
линеаментов
Слайд 100Пример автоматического обнаружения зданий с летательного аппарата
Фильтрация по размеру
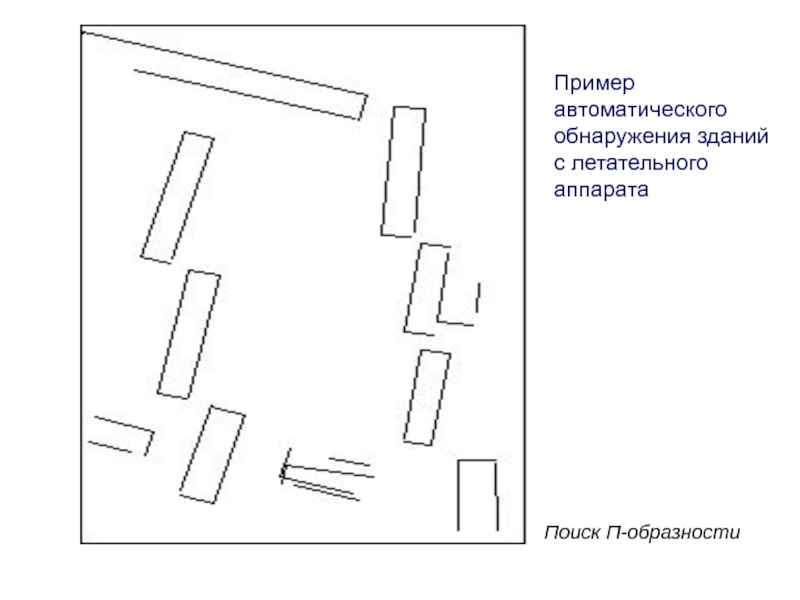
Слайд 101Пример автоматического обнаружения зданий с летательного аппарата
Поиск П-образности
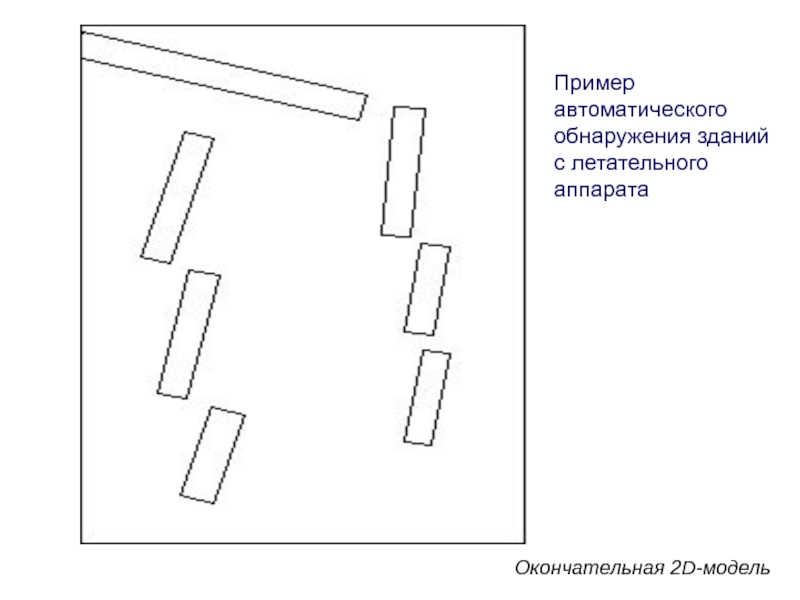
Слайд 102Пример автоматического обнаружения зданий с летательного аппарата
Окончательная 2D-модель
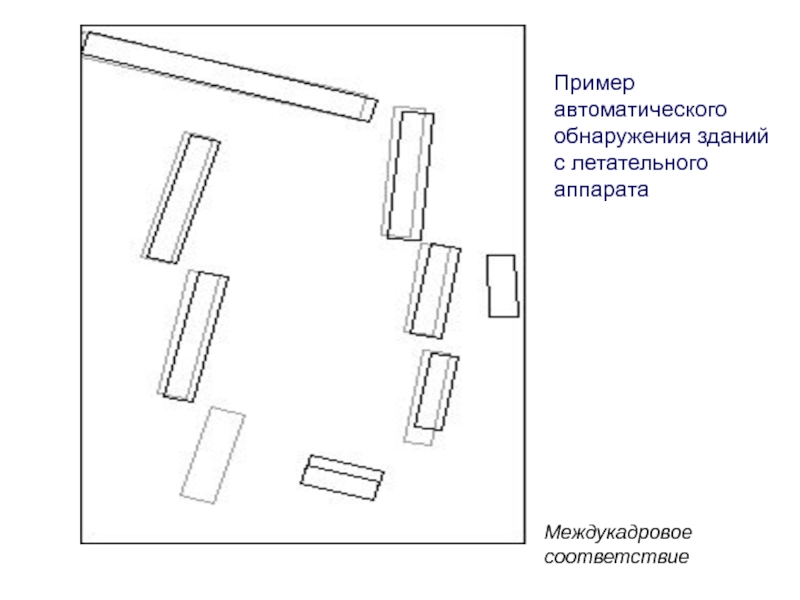
Слайд 103Пример автоматического обнаружения зданий с летательного аппарата
Междукадровое соответствие