Прямые

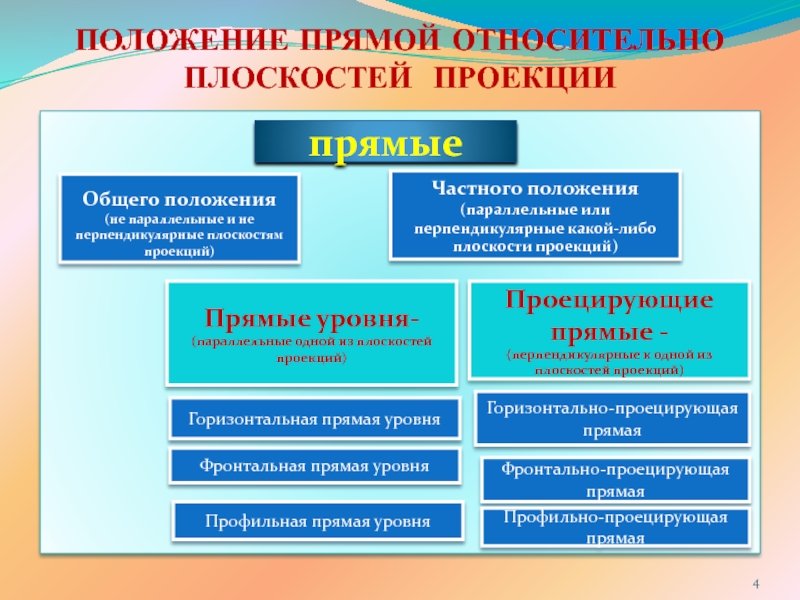
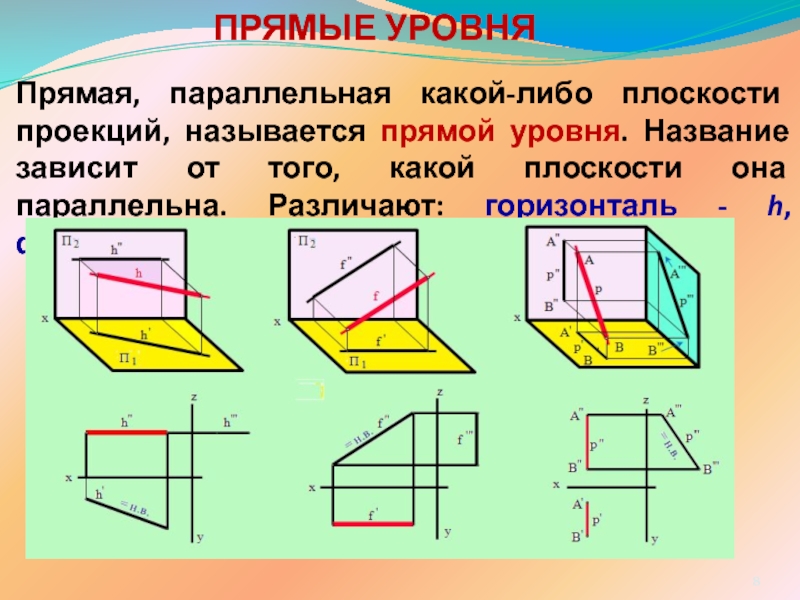
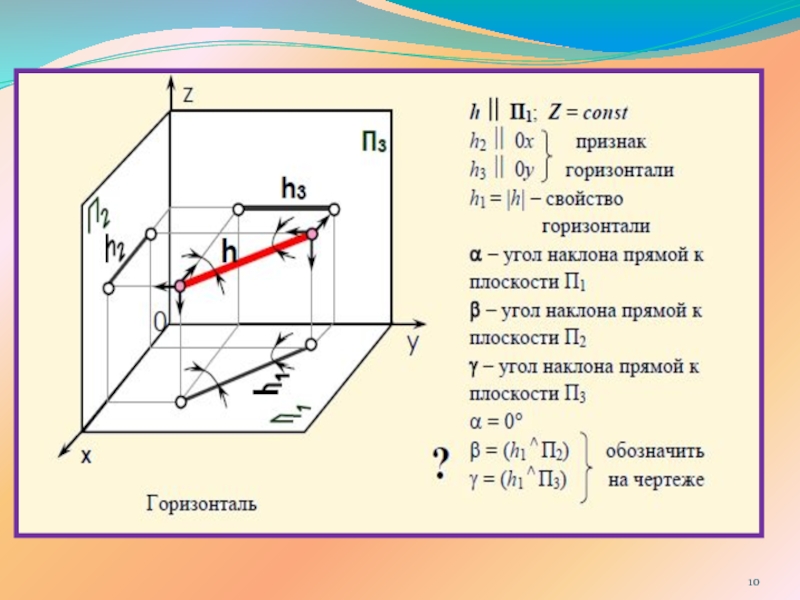
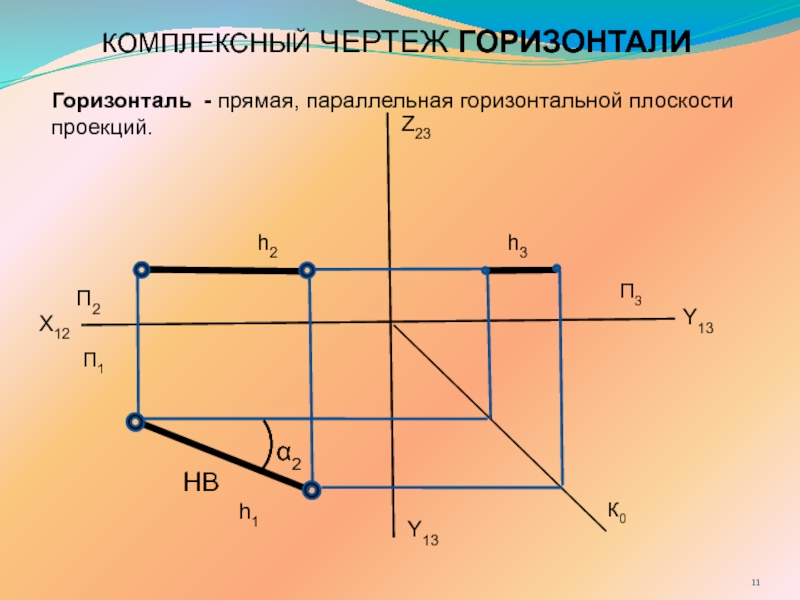
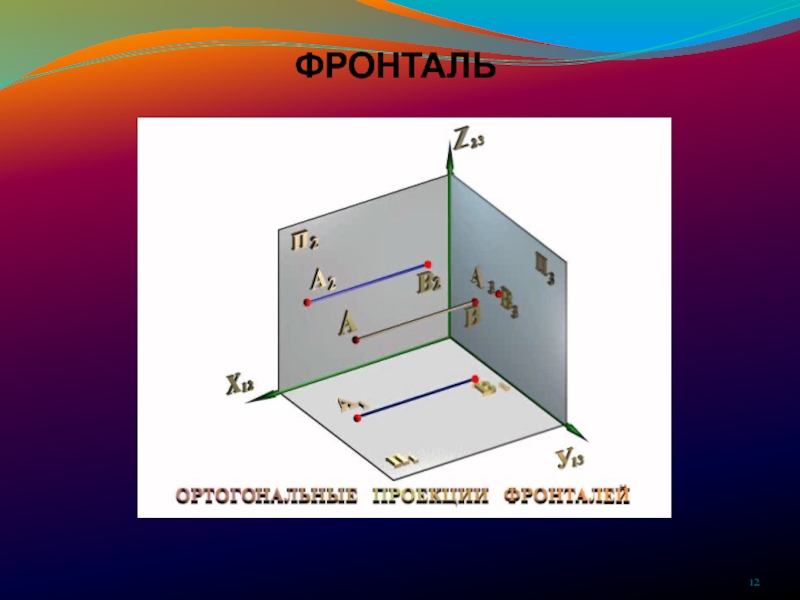
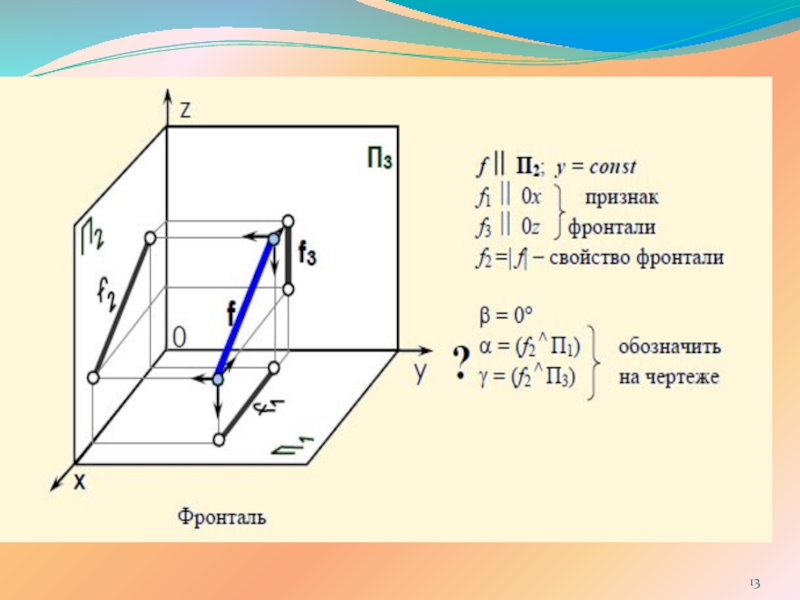
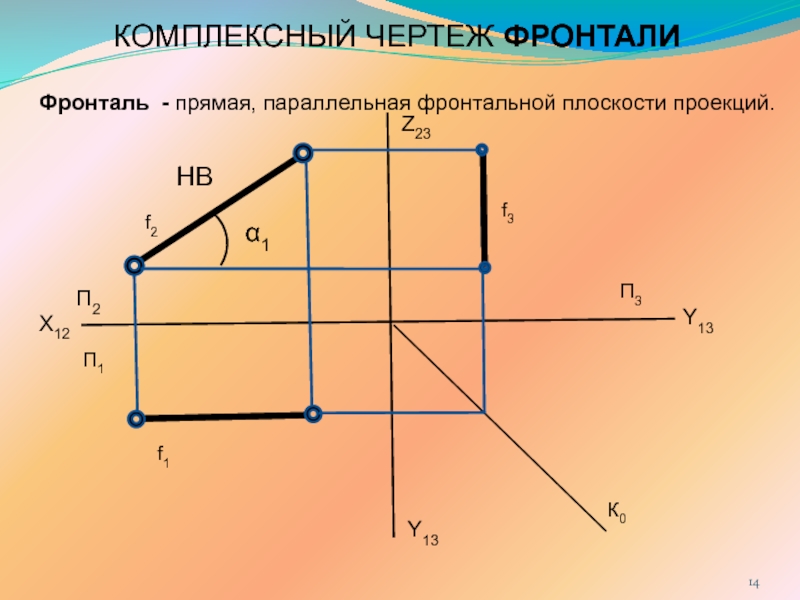
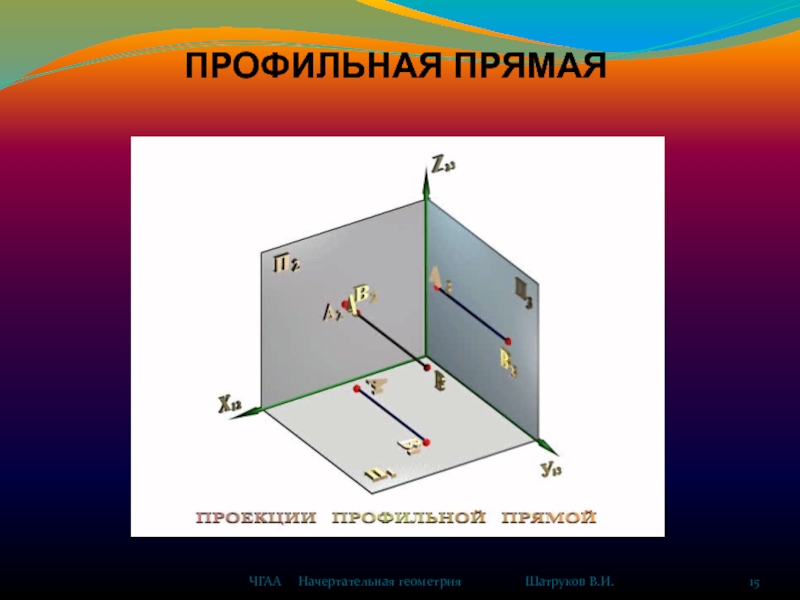
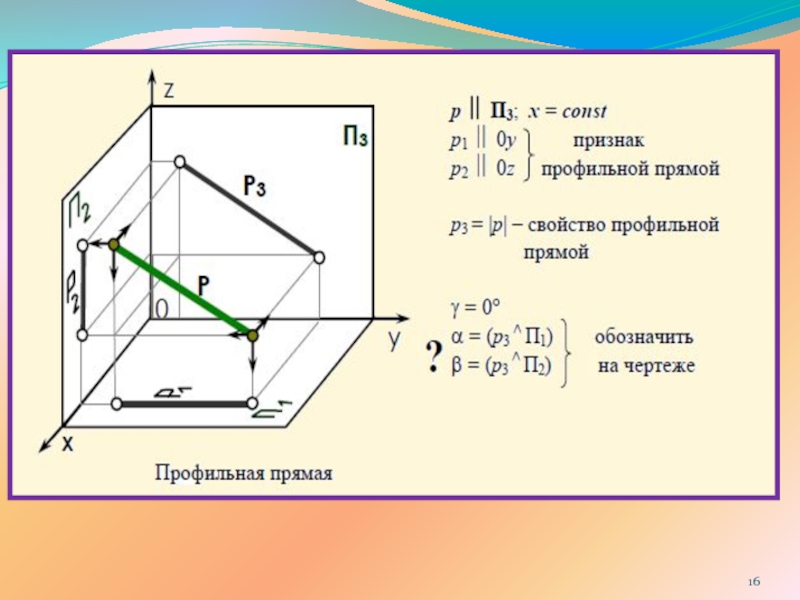
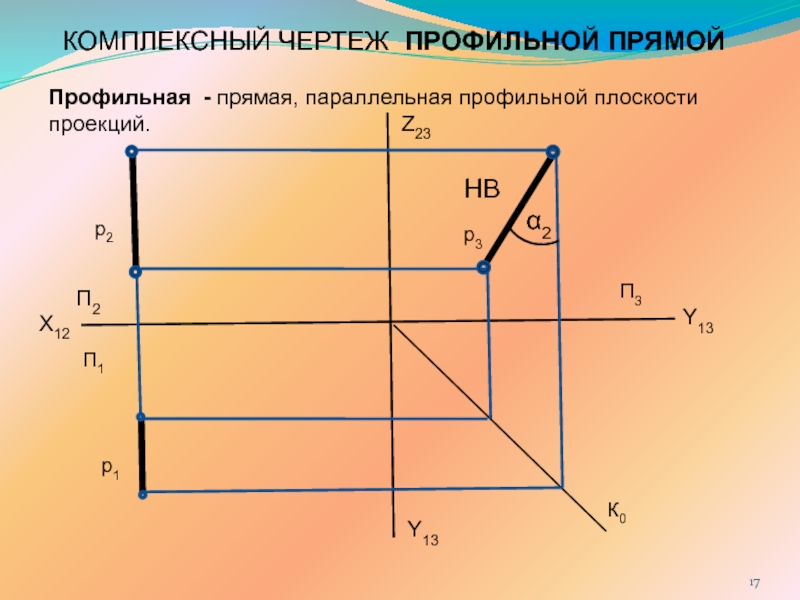
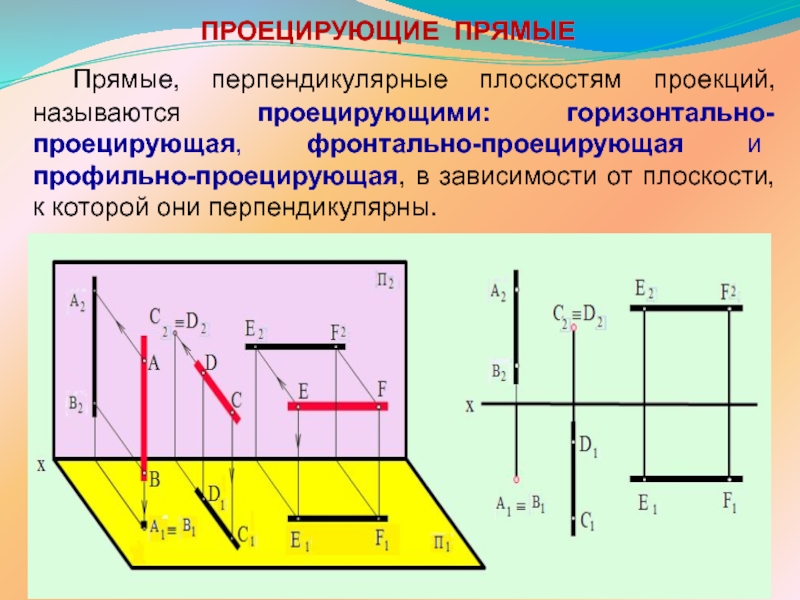
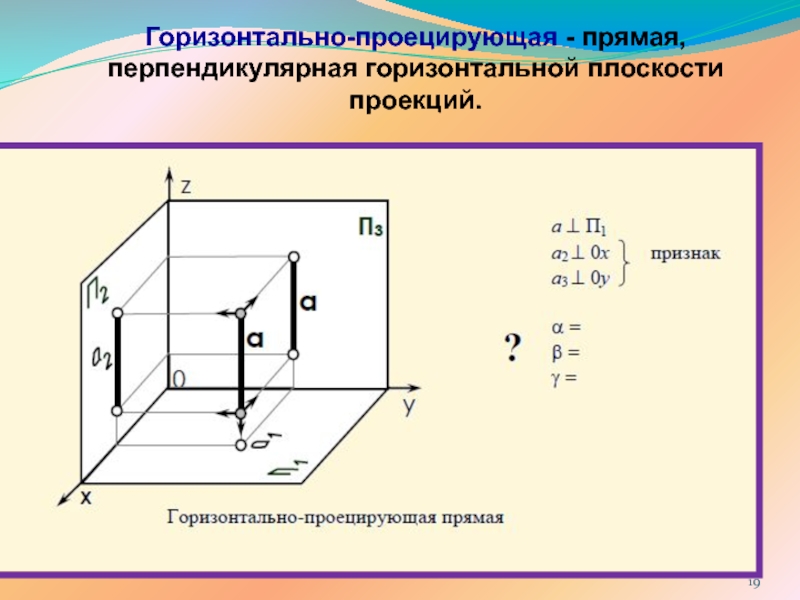
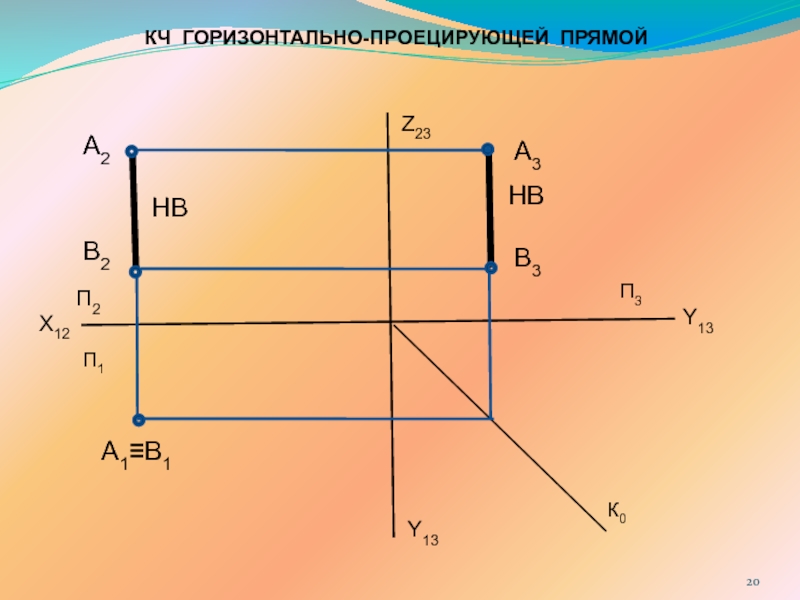
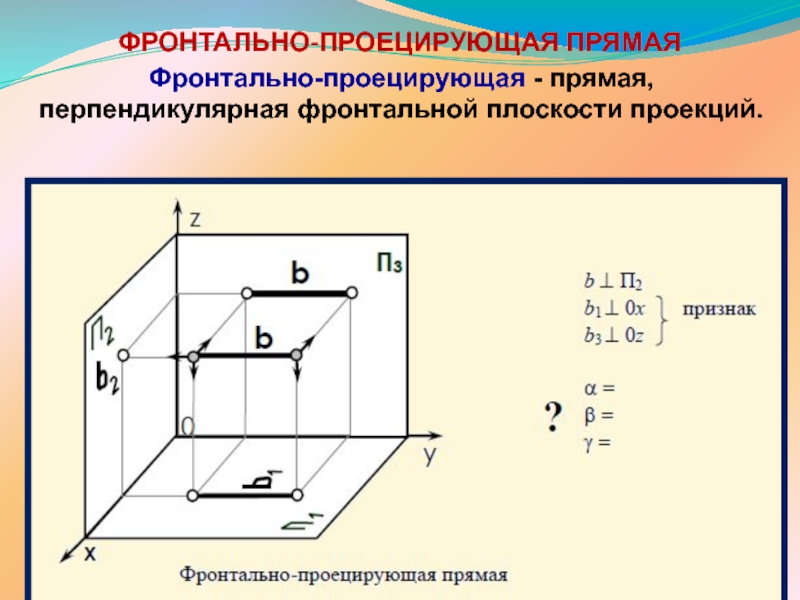
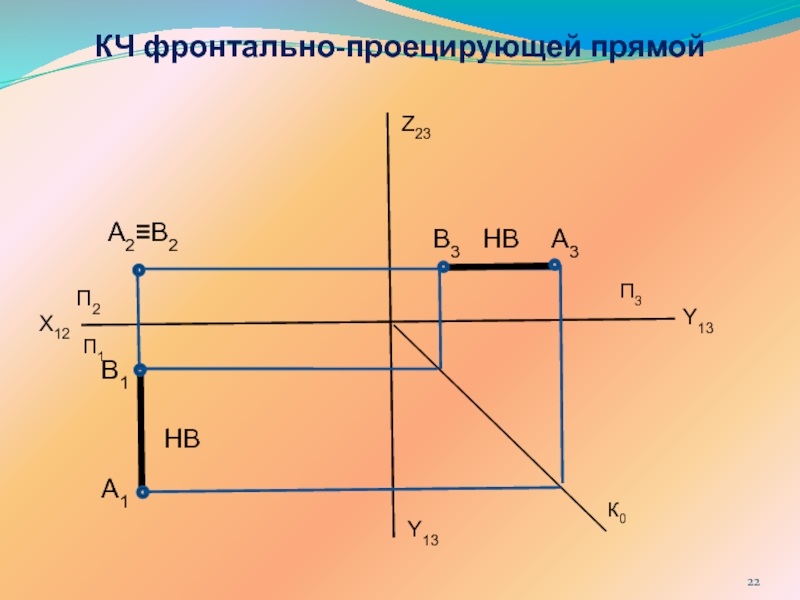
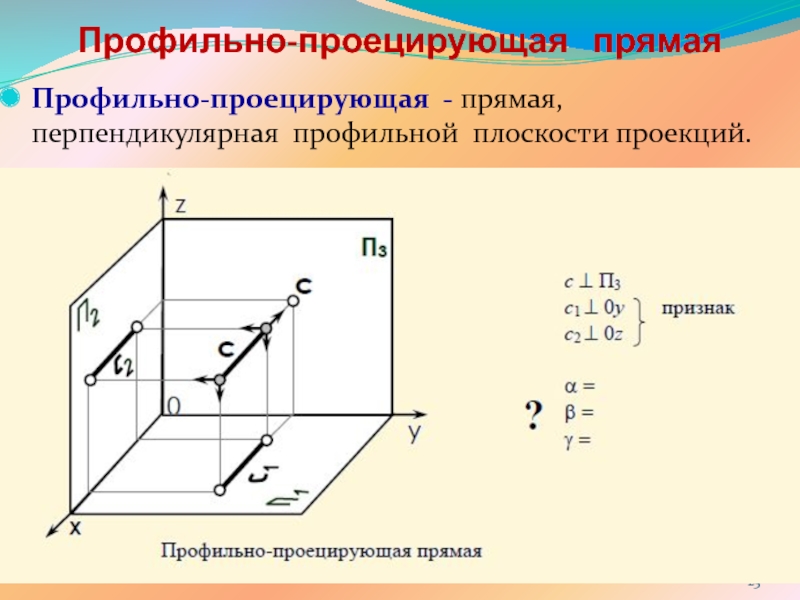
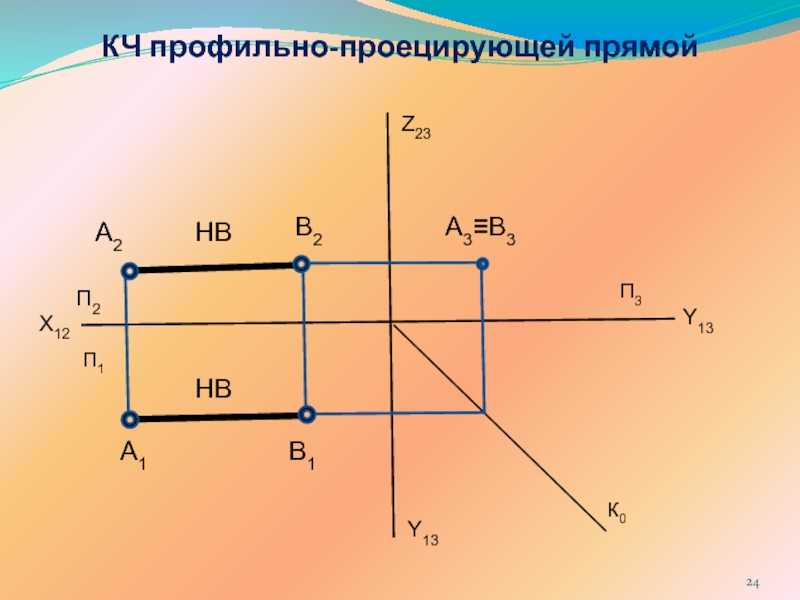
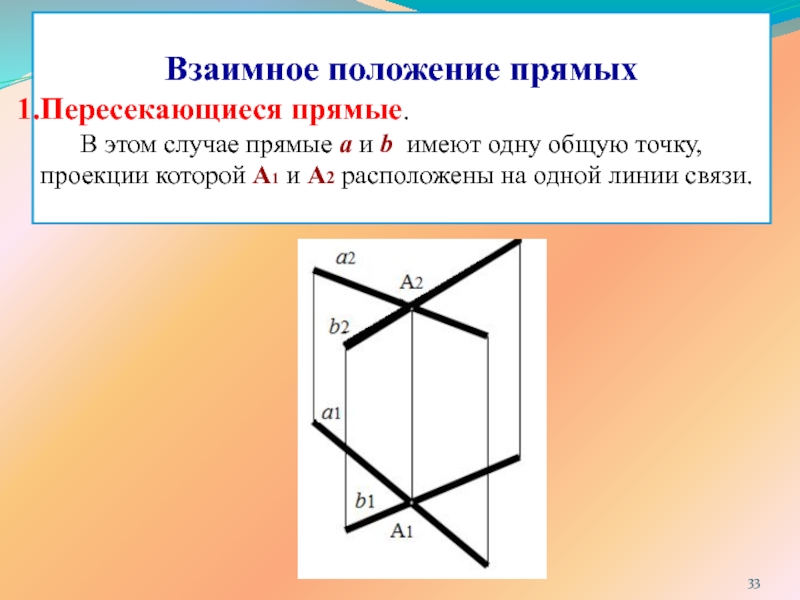
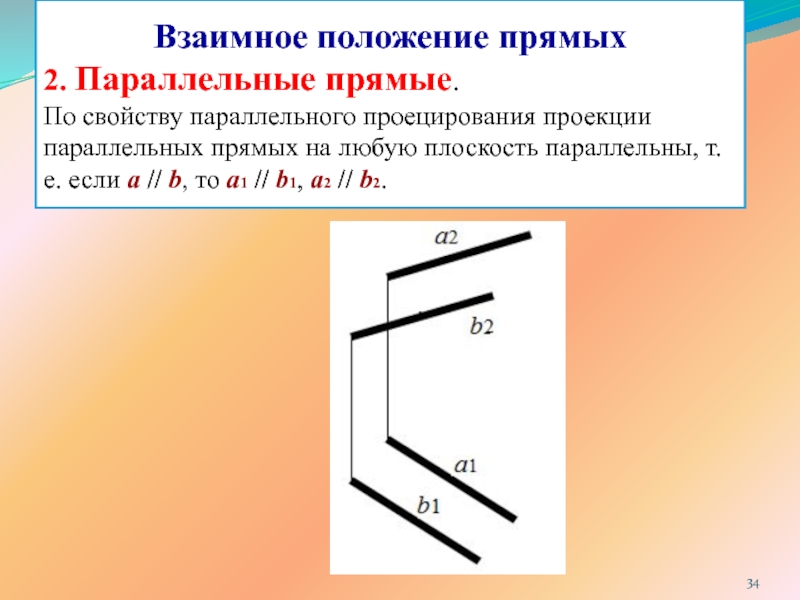
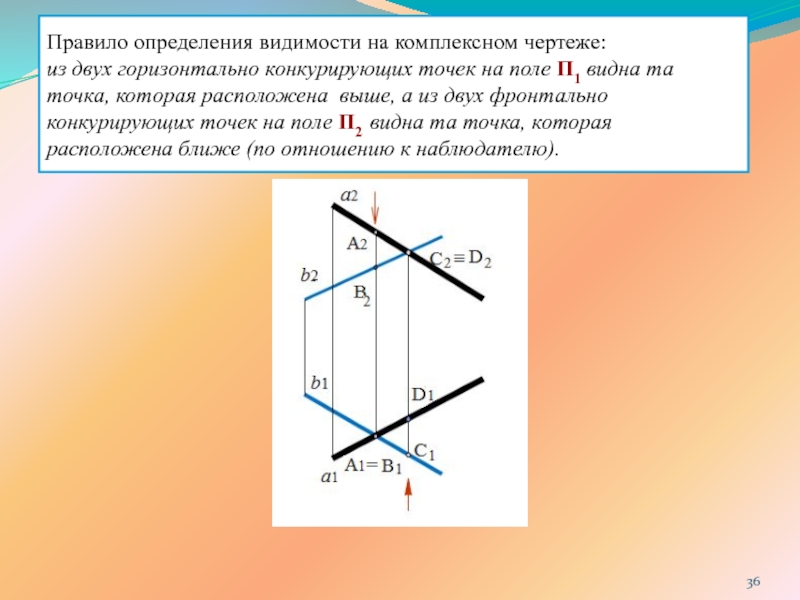
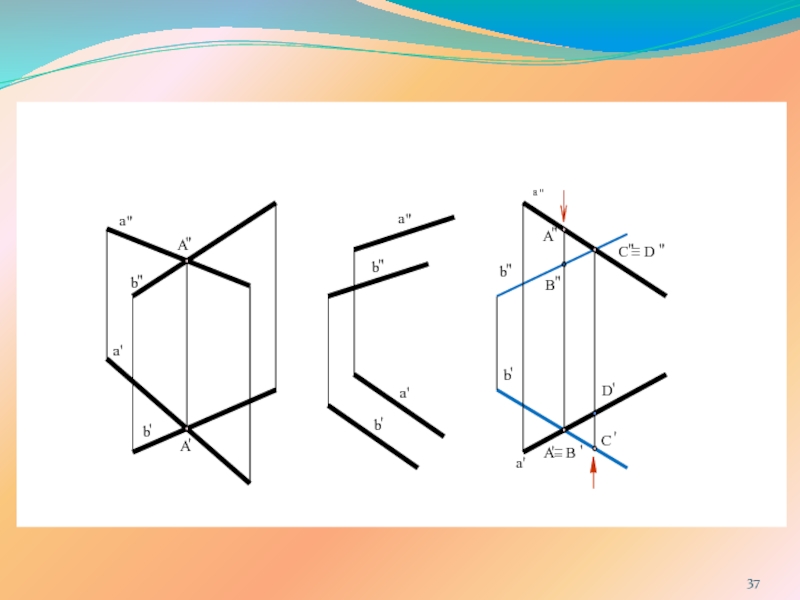
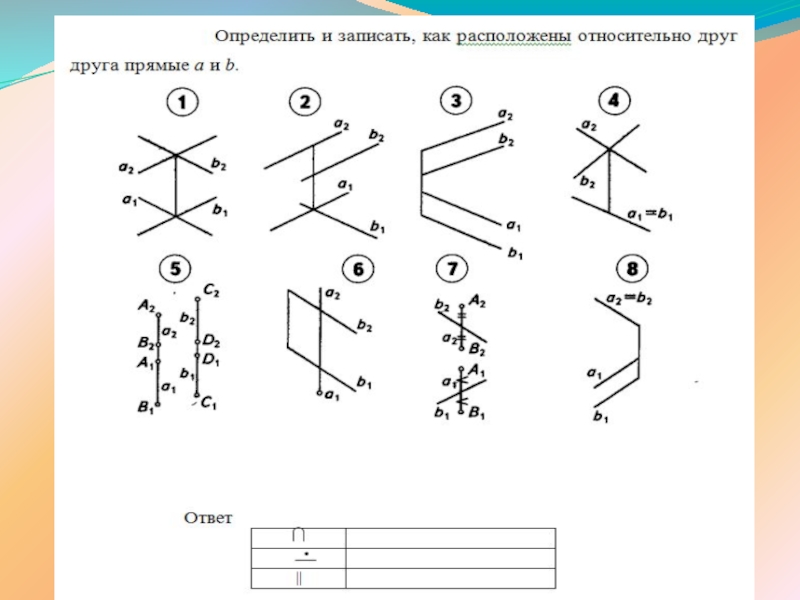
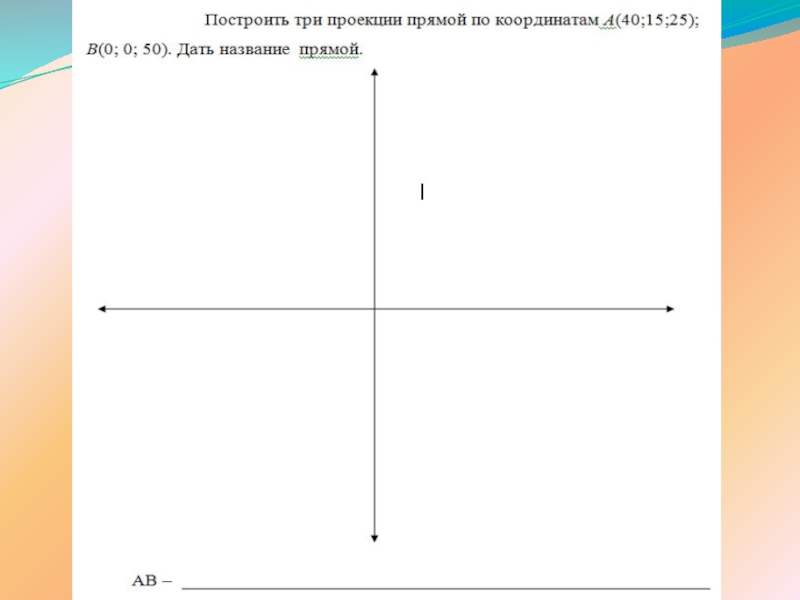
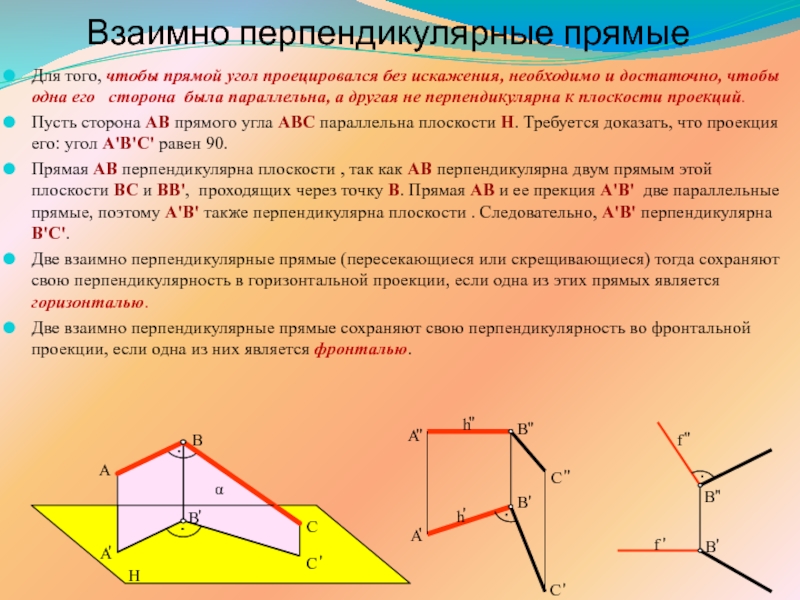
ПРЯМОЙ ЛИНИИ
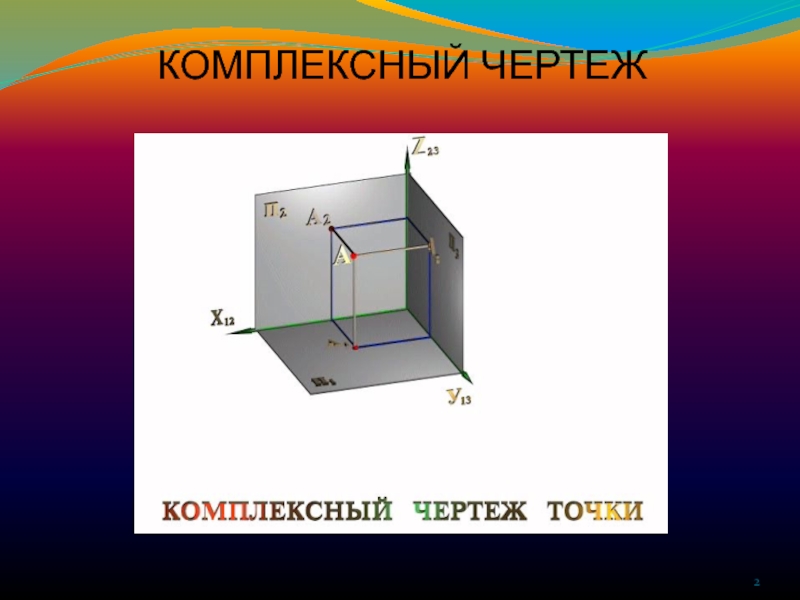
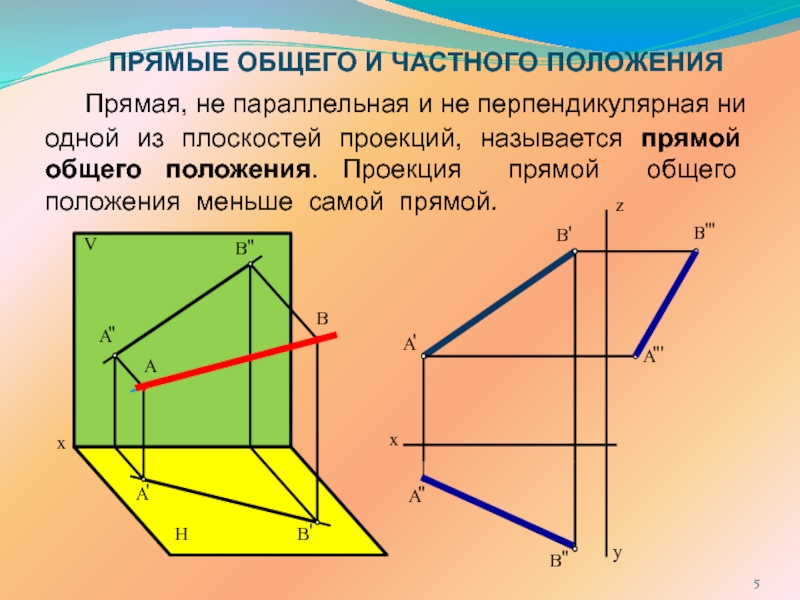
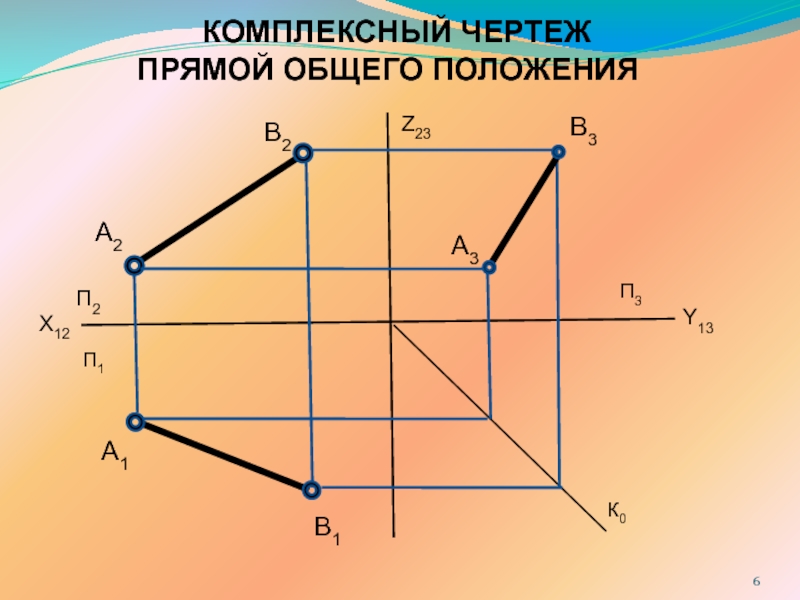
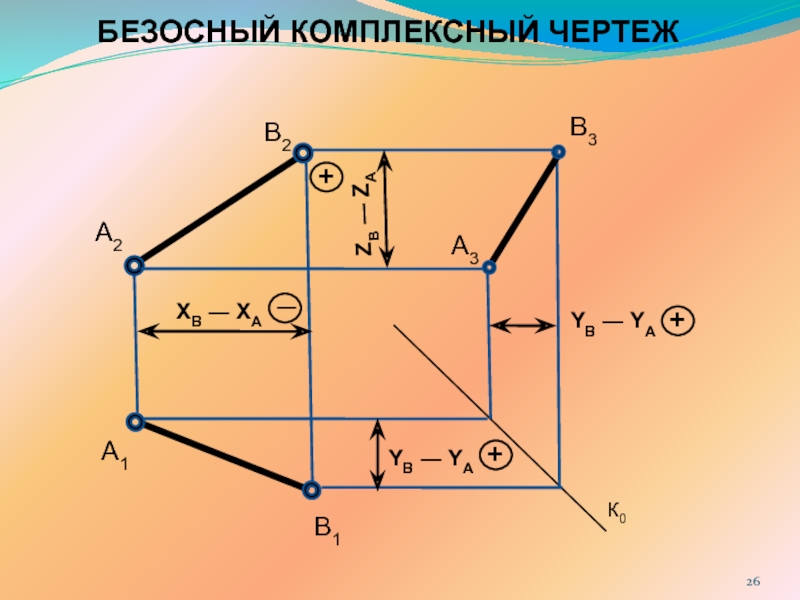
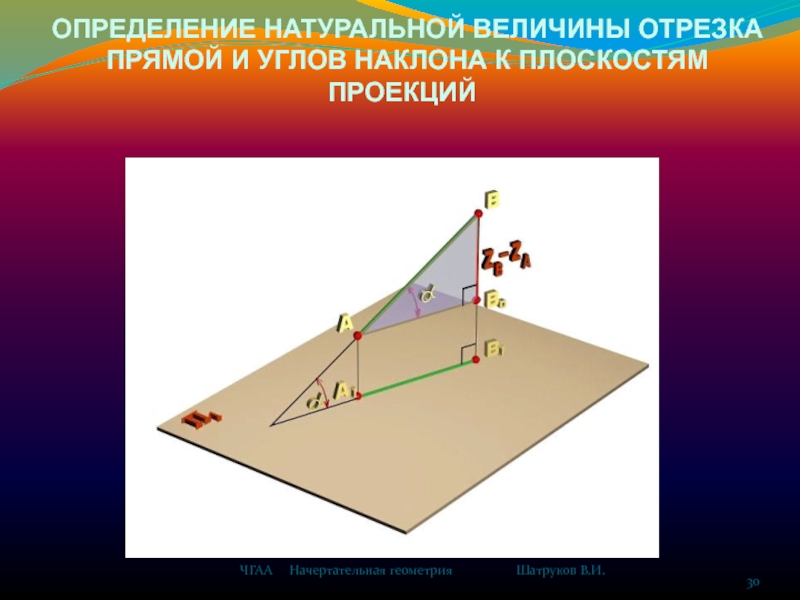
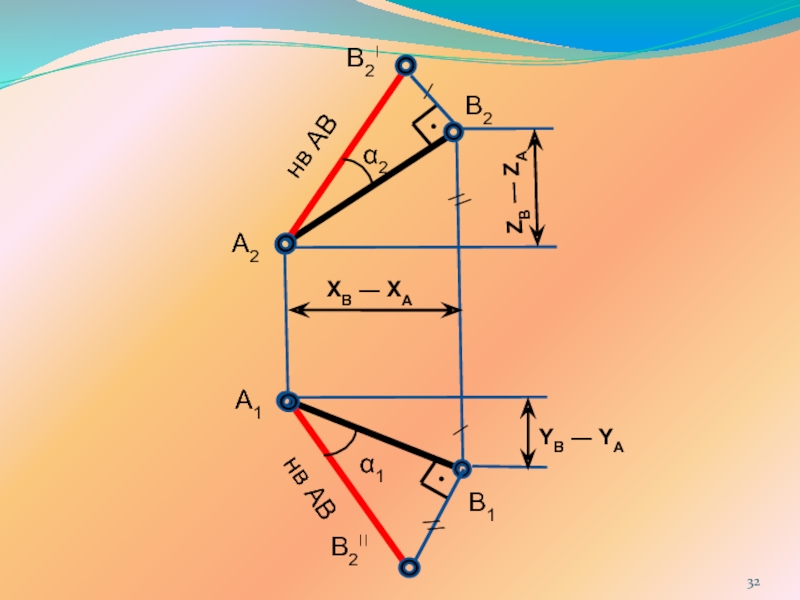
Прямая линия в пространстве определяется положением двух

ее точек, например т.А и т. B.

Следовательно, для получения соответственно горизонтальной и фронтальной проекций прямой АВ, достаточно выполнить комплексный чертеж точек А и В, а затем соединить одноименные проекции точек прямыми линиями.

плоскостям проекций)

Частного положения
(параллельные или перпендикулярные какой-либо плоскости проекций)
Прямые уровня-
(параллельные

одной из плоскостей проекций)

Проецирующие прямые -
(перпендикулярные к одной из плоскостей проекций)

Горизонтальная прямая уровня

Фронтальная прямая уровня

Профильная прямая уровня

Горизонтально-проецирующая прямая

Фронтально-проецирующая прямая

Профильно-проецирующая прямая

ни одной из плоскостей проекций, называется прямой общего положения. Проекция

прямой общего положения меньше самой прямой.

Основы проектирования СХМ
ПРЯМЫЕ ЧАСТНОГО ПОЛОЖЕНИЯ

зависит от того, какой плоскости она параллельна. Различают: горизонталь -

h, фронталь - f и профильная прямая - р.

Шатруков В.И.

профильно-проецирующая, в зависимости от плоскости, к которой они перпендикулярны.

ПРОЕКЦИЙ
ЧГАА Начертательная геометрия

Шатруков В.И.

∕
∕ ∕
нв AB
B׀2
B׀׀2

α1

прямые a и b имеют одну общую точку, проекции которой

A1 и A2 расположены на одной линии связи.

параллельных прямых на любую плоскость параллельны, т.е. если a //

b, то a1 // b1, a2 // b2.

их одноименные проекции могут пересекаться в точках, не лежащих на

одной линии связи: две точки А и В - горизонтально конкурирующие точки, две точки C и D - фронтально конкурирующие. Как видно из чертежа , точка А расположена над точкой В; следовательно, прямая a проходит над прямой b. Точка С расположена перед (ближе к зрителю) точкой D, следовательно, прямая b проходит в этом месте впереди прямой a.

на поле П1 видна та точка, которая расположена выше, а

из двух фронтально конкурирующих точек на поле П2 видна та точка, которая расположена ближе (по отношению к наблюдателю).

необходимо и достаточно, чтобы одна его сторона была параллельна,

а другая не перпендикулярна к плоскости проекций.
Пусть сторона AB прямого угла ABC параллельна плоскости H. Требуется доказать, что проекция его: угол A'B'C' равен 90.
Прямая АВ перпендикулярна плоскости , так как АВ перпендикулярна двум прямым этой плоскости BC и BB', проходящих через точку В. Прямая АВ и ее прекция А'В' две параллельные прямые, поэтому А'B' также перпендикулярна плоскости . Следовательно, A'B' перпендикулярна B'C'.
Две взаимно перпендикулярные прямые (пересекающиеся или скрещивающиеся) тогда сохраняют свою перпендикулярность в горизонтальной проекции, если одна из этих прямых является горизонталью.
Две взаимно перпендикулярные прямые сохраняют свою перпендикулярность во фронтальной проекции, если одна из них является фронталью.