Слайд 1QUANTUM CHAOS IN NUCLEAR PHYSICS
Слайд 2Investigation of quantum chaos in nuclear physics is strongly hampered
by the absence of even the definition of quantum chaos,
not to mention the numerical criterion of the quantum chaoticity.
These drawbacks are caused by the fact that the present concept of chaos is based on the Lyapunov trajectory instability. For the classical chaotic system a small variation of initial conditions causes exponential divergence of the trajectories in the phase space. The distance between two initially close trajectories increases as , Λ - Lyapunov exponent.
Trajectory is smeared by the uncertainty principle. Therefore:
“Incorrect term “quantum chaos” means quantum phenomena characteristic of the classically chaotic systems, quantum signatures of the classical chaos.” (M.Berry (1991)).
Search for the “quantum signatures” of the classical chaos:
1. Take two classical systems - regular and chaotic.
2. Construct and solve the two corresponding Schrödinger equations.
3. Compare all the properties of the solutions in hope to find something distinguishing the quantum analogue of the classically chaotic system.
The only such signature found in 40 years of intensive search turned out to be the level distribution law.

Слайд 3
For the quantum analogues of the classically chaotic systems -
Wigner law
for
-- level repulsion (D - average level spacing)
This immediately brings us to nuclear physics. Back in 1950-ies Wigner developed the random matrix approach to the statistical description of neutron resonances in compound nuclei and derived the above law for the distribution of those resonances.
Sometimes - statements made that for regular systems Poisson law
Since the majority of natural systems - intermediate between the regular and chaotic (“soft chaos”), attempts to invent the interpolation formulae between the two laws. However it was shown that for lots of the quantum analogs of regular systems Poisson law does not apply.
Слайд 4
Since the main feature of compound resonances is their complex
structure, attempts were made to invent different measures of their
wave functions’ complexity as the measures of quantum chaoticity. Still the main drawback - lack of the quantum chaos definition. The definition “quantum signatures of the classical chaos” seems quite strange and wrong. Nobody considers the laws of relativistic mechanics as “relativistic signatures” of the classical mechanics laws.
Classical mechanics is a particular limiting case of quantum mechanics and not vice versa. In transferring from quantum to classical pictures we are coarsening our description and loosing a lot of purely quantum effects instead of discovering new purely classical phenomena. More natural - to look for a more general definition of chaos which holds both for quantum and classical mechanics.
Thus our idea is to stop clinging to Lyapunov trajectory instability as the main source of chaos in classical mechanics.
Слайд 5There is a well-known Liouville-Arnold theorem in classical mechanics which
states that a regular system with N degrees of freedom
should also have M=N global integrals of motion (conservation laws) connected with the symmetries of the system’s Hamiltonian. I.e. the regular system possesses a sufficiently high symmetry to have the number M of integrals of motion equal to the number N of its degrees of freedom.
Contrary to trajectory, the notion of symmetry applies to all the fields of physics, including classical an quantum mechanics. As a consequence of this theorem one can define the quantum regular system as that whose Hamiltonian possesses sufficiently high symmetry to have the number M of conservation laws (“good quantum numbers”) which is equal to the number N of its degrees of freedom. If one switches on the perturbation which destroys the system’s symmetries so that M
Thus we suggest to define as chaotic the quantum system whose symmetry is so low that M
Слайд 6Let us apply this definition to nuclei.
Actually each system of
more than 2 interacting particles has less integrals of motion
than its degrees of freedom. Therefore all the nuclei heavier than deuteron are quantum chaotic systems. The neutron resonances of medium and heavy nuclei for whom Wigner stated his level distribution law have only 3 good quantum numbers: energy, total spin and parity (although now we know that their parity might be violated). The number of quasi-particles defining the structure of the low-lying neutron resonances is 8–10. Therefore these resonances are of course quite typical examples of the quantum chaotic systems.
Moreover, the theory of the neutron strength function describing these resonances allows to introduce the quantitative measure of the quantum chaoticity. Indeed, bearing in mind the Hartree-Fock method which proved quite successful in constructing a self-consistent mean field in atomic physics, we can try to represent the Hamiltonian of a compound nuclear system as
were H0 describes the motion of noninteracting nucleons in their mean field, while V takes into account residual pair interactions, which can not be included in the mean field.

Слайд 7We can now seek the wave functions of the system
(eigenfunctions of the full Hamiltonian H )
as a superposition of various configurations of the Hamiltonian H0 describing noninteracting particles. Expand now the wave functions of the total Hamiltonian over the basis of the “regular”
states :
and consider the probability to find the initial regular single-quasiparticle component in the eigenfunctions .
The neutron strength function theory shows that this probability is concentrated in the energy interval around the “initial” value . The strength function under rather general assumptions shows how the regular state is fragmented over the states of the chaotic system:
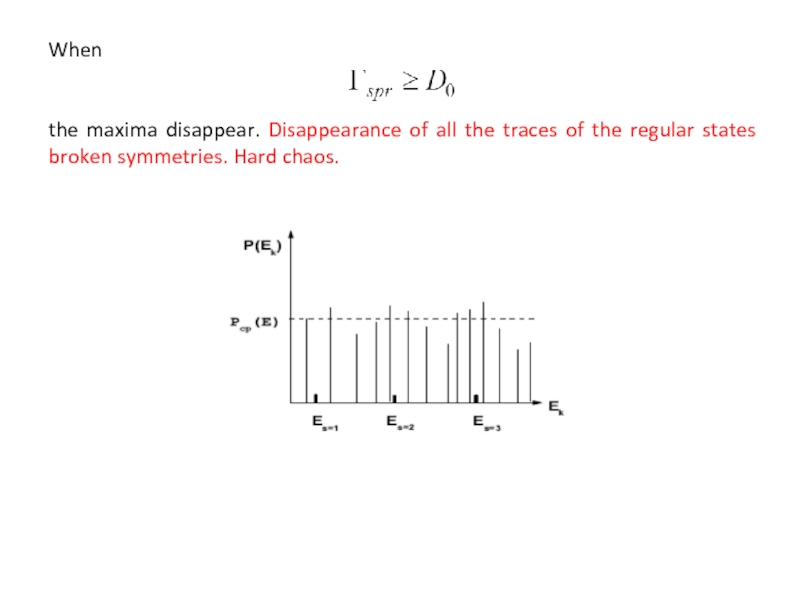
Слайд 8When the localization interval
is smaller than the average level distance
of the regular system
the strength function peaks at show vivid traces of the initial regular
states with quantum numbers . Although the symmetry of the regular system is formally broken, its traces are quite visible - soft chaos.
Слайд 9When
the maxima disappear. Disappearance of all the traces of the
regular states broken symmetries. Hard chaos.
Слайд 10Thus the dimensionless parameter
is a natural measure of quantum
chaoticity.
It can be shown that in the classical limit
:
and
is the period of the classical orbit.
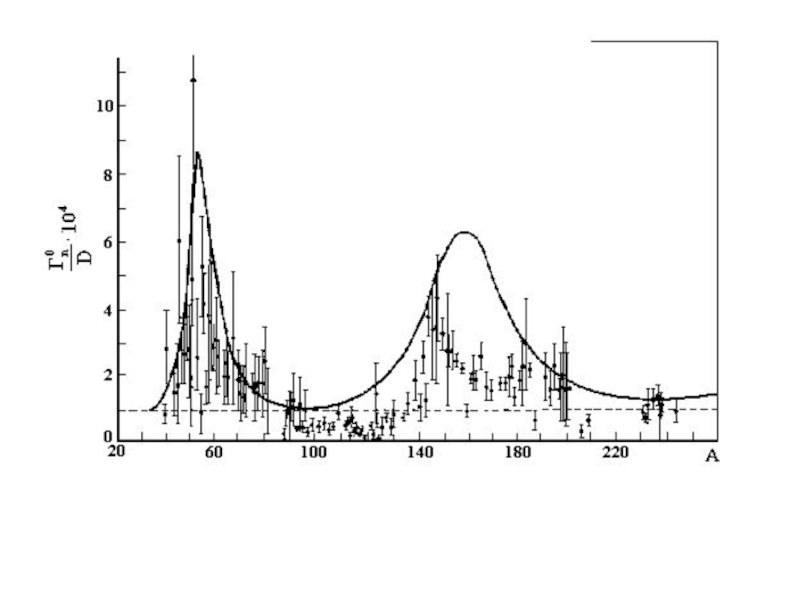
Position of the s- resonances in nuclei:
Thus one can either fix the nucleus A (i.e. R) and see the dependence , or fix E≈1 eV and look for the dependence Neutron strength function for s-wave neutrons.
Слайд 12
In nuclei A=50 and A=160 single particle states 3s and
4s appear at neutron energy ≈1 eV. Nuclei with
140
Typical example of weak chaos: the symmetries of the spherical mean
field are broken by the pair N-N interaction , but the traces of those symmetries are still clearly seen (quantum analog of classical KAM theorem).
imaginary part of the optical potential.
Therefore for neutron resonances in medium and heavy nuclei
MeV, so chaoticity parameter increases with increasing excitation energy, but remains less than unity up to ≈100 MeV as well as for the deepest single-hole states.
, so chaoticity parameter increases with increasing A.
However classification in terms of the chaoticity amount is not meaningful in itself.
Слайд 13What really matters is the theoretical approach to quantum chaotic
systems.
Our interest in chaos appeared because we realized that there
is no sharp border between the regularity and chaos. Practically all the systems in Nature are more or less chaotic.
We see that nuclear physics had to deal with quantum chaotic objects for more than half a century. Not only does the experience of nuclear physics enable us to clarify connections between symmetries and chaos, but it also proposes the effective methods to deal with Schrödinger equations for various degrees of chaoticity (various values of ). is the principal small parameter in nuclear physics, which makes the shell-model basis most adequate because of its rapid convergence and allows to use optical model as the main component of various reaction theories.
For it is possible to use statistical approaches employing random matrices’ methods or equation of Fokker- Plank.
Therefore the matter of quantum chaos in nuclear physics is of interest only because nuclear physics serves a good example of operating with quantum chaotic systems to all the fields of science which had already faced quantum chaos or will definitely face it in future.