Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Р е ш е н и е п р а к т и ч е с к и х з а д а ч
Содержание
- 1. Р е ш е н и е п р а к т и ч е с к и х з а д а ч
- 2. Решение практических задач #репетитор_по_математике_онлайнОбъектами этой задачи являются
- 3. Слайд 3
- 4. Слайд 4
- 5. Решение практических задач #репетитор_по_математике_онлайнСм. на рисунки. Наша
- 6. Решение практических задач #репетитор_по_математике_онлайнРешение:Наши треугольники АВС и КМР - подобные, по первому признаку подобия
- 7. Решение практических задач #репетитор_по_математике_онлайнРекомендованная теория:! Первый признак
- 8. Скачать презентанцию
Решение практических задач #репетитор_по_математике_онлайнОбъектами этой задачи являются вполне реальные предметы: колокольня и фонарный столб. Поэтому это практическая задача. Чтобы её решить с помощью математики, надо построить соответствующую ей математическую задачу, которая
Слайды и текст этой презентации
Слайд 2Решение практических задач
#репетитор_по_математике_онлайн
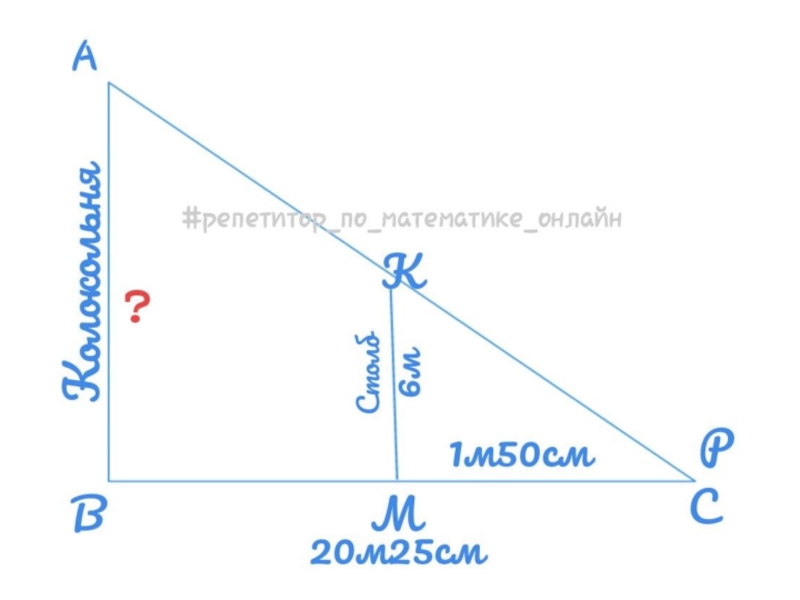
Объектами этой задачи являются вполне реальные предметы: колокольня
и фонарный столб. Поэтому это практическая задача. Чтобы её решить
с помощью математики, надо построить соответствующую ей математическую задачу, которая получается путём отвлечения от конкретных особенностей реальных предметов и заменой их математическими объектами. В данном случае объекты: колокольню, столб и тени падающие от них на землю, можно рассматривать как стороны треугольника. Считая, что поверхность земли есть прямая, а отрезки, изображающие колокольню и столб, перпендикулярны к этой прямой, соответственно длина падающей тени и объектов: колокольня и столб, образуют прямые углы, получим такую математическую задачу.Слайд 5Решение практических задач
#репетитор_по_математике_онлайн
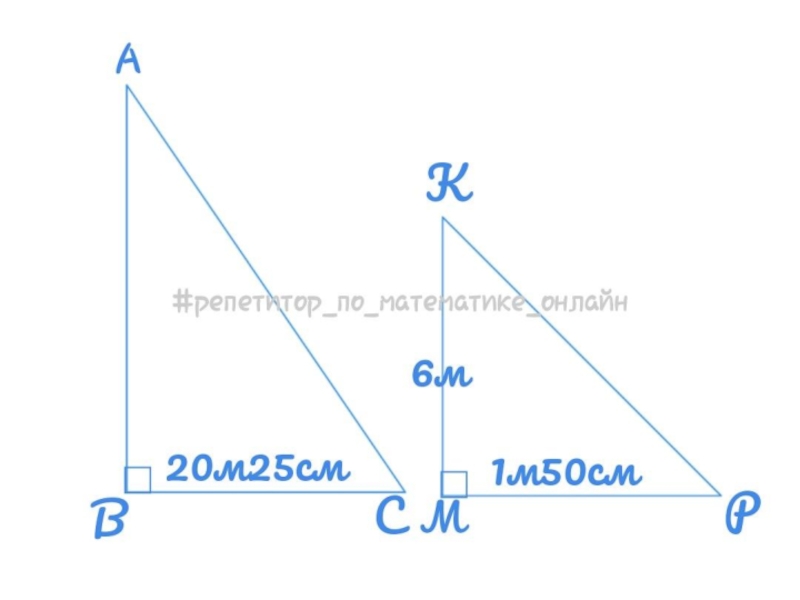
См. на рисунки. Наша высота колокольни - это
сторона АВ, падающая тень от колокольни - сторона ВС, высота
столба - это сторона КМ, а падающая тень от столба - сторона МР. А так как столб стоит рядом с колокольней, то тень столба, скорее всего, принадлежит части тени колокольни.Математическая задача. Даны два треугольника АВС и КМР, где <В = < М = 90°, ВС = 20м 25 см, МР = 1м 50 см, КМ = 6м. Найдите второй катет треугольника АВС.
Соответственно нам требуется найти катет АВ, который и будет являться высотой колокольни.
Слайд 6Решение практических задач
#репетитор_по_математике_онлайн
Решение:
Наши треугольники АВС и КМР - подобные, по
первому признаку подобия
< Р, сответственно ВС : МР = АВ : КМ, воспользуемся основным свойством пропорции и получим МР • АВ = ВС • КМ => АВ = (ВС • КМ): МР, в полученное равенство подставим известные данные:20м25см = 20,25 м; 1м50см = 1,5м
АВ = (20,25 • 6) : 1,5 = 81 м
Слайд 7Решение практических задач
#репетитор_по_математике_онлайн
Рекомендованная теория:
! Первый признак подобия треугольников: по двум
углам.
Если два угла одного треугольника равны двум углам другого
тр-ка, то такие треугольники подобны.! Прямая, параллельная стороне треугольника и пересекающая его две другие стороны, отсекает от данного треугольника ему подобный.