Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Расчет термодинамических средних и оценка погрешности Расчет термодинамических средних. Термализация. Расчет погрешностей. Авто
Содержание
- 1. Расчет термодинамических средних и оценка погрешности Расчет термодинамических средних. Термализация. Расчет погрешностей. Авто
- 2. ТермализацияОтвет не должен зависеть от начального состояния
- 3. Несмещенная оценкаРасчет погрешности через среднеквадратичное отклонение:Эта формула
- 4. Автокорреляционный анализУсреднение по конфигурациям эквивалентно интегрированию вдоль
- 5. Автокорреляционный анализРасчет погрешности:Автокорреляционная функция физической величины:Принцип ослабления
- 6. Метод разбиенийЧастичное среднее для каждой части:Дисперсия, автокорреляционное время и оценка погрешности:Обычная дисперсия по представительной выборке:
- 7. Метод разбиенийВ пределе r→∞ автокорреляционное время и
- 8. Метод 1/2 файлаТекущее среднее значение:Погрешность расчета:
- 9. Метод 1/2 файлаОценка автокорреляционного времени:Оценка автокорреляционного времени
- 10. Автокорреляционное время и погрешность для модели ИзингаЗависимости
- 11. Скачать презентанцию
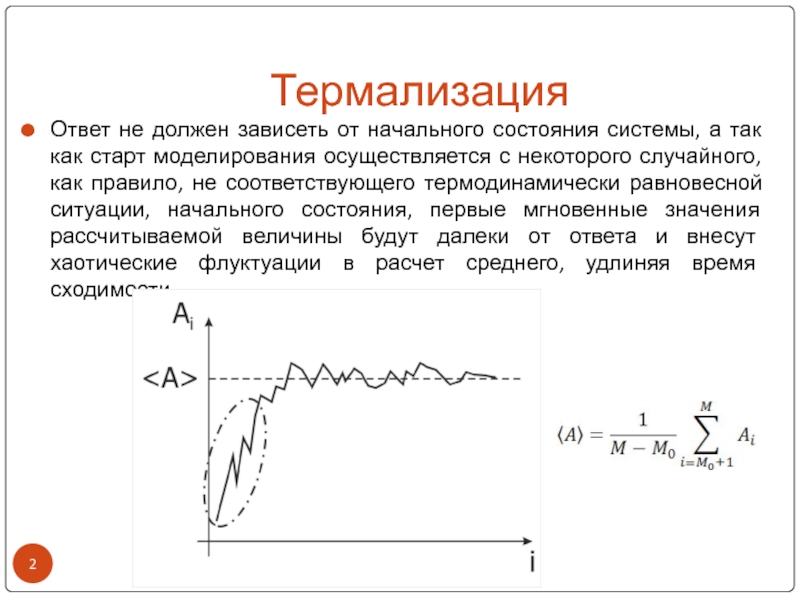
ТермализацияОтвет не должен зависеть от начального состояния системы, а так как старт моделирования осуществляется с некоторого случайного, как правило, не соответствующего термодинамически равновесной ситуации, начального состояния, первые мгновенные значения рассчитываемой величины
Слайды и текст этой презентации
Слайд 1Расчет термодинамических средних. Термализация. Расчет погрешностей. Автокорреляционный анализ
2.9. Расчет термодинамических
средних и оценка погрешности
Слайд 2Термализация
Ответ не должен зависеть от начального состояния системы, а так
как старт моделирования осуществляется с некоторого случайного, как правило, не
соответствующего термодинамически равновесной ситуации, начального состояния, первые мгновенные значения рассчитываемой величины будут далеки от ответа и внесут хаотические флуктуации в расчет среднего, удлиняя время сходимости
Слайд 3Несмещенная оценка
Расчет погрешности через среднеквадратичное отклонение:
Эта формула справедлива для независимых
случайных величин и приведет к некорректному результату для событий, составляющих
марковскую цепь, так как каждое следующее мгновенное значение имеет определенную корреляцию с предыдущимКорреляция между отельными событиями марковской цепи Ai и Ai+k ослабляется с увеличением k
Оценка корреляций между различными мгновенными значениями Ai осуществляется при помощи автокорреляционной функции
Минимальное количество итераций, необходимое для реализации двух статистически независимых мгновенных значений Ai, определяется автокорреляционным временем расчета величины A
Слайд 4Автокорреляционный анализ
Усреднение по конфигурациям эквивалентно интегрированию вдоль стохастической фазовой траектории
в фазовом пространстве:
Если схема алгоритма эргодическая, усреднение по времени эквивалентно
усреднению с гиббсовскими весами по полному ансамблю состояний системы:Корреляционная функция двух физических величин:
Среднее по ансамблю:
Слайд 5Автокорреляционный анализ
Расчет погрешности:
Автокорреляционная функция физической величины:
Принцип ослабления корреляций при увеличении
времени наблюдения между измерениями:
Автокорреляционное время физической величины:
Чем меньше автокорреляционное время,
тем быстрее сходимость:
Слайд 6Метод разбиений
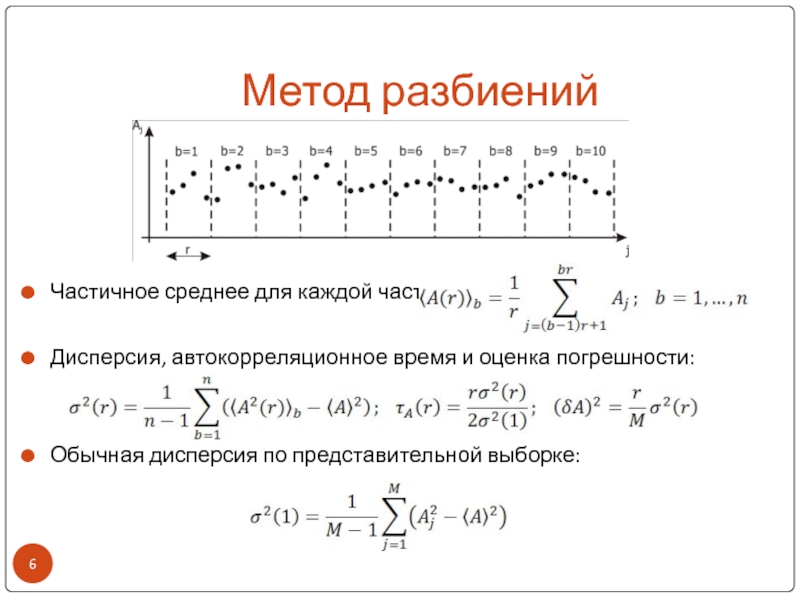
Частичное среднее для каждой части:
Дисперсия, автокорреляционное время и оценка
погрешности:
Обычная дисперсия по представительной выборке:
Слайд 7Метод разбиений
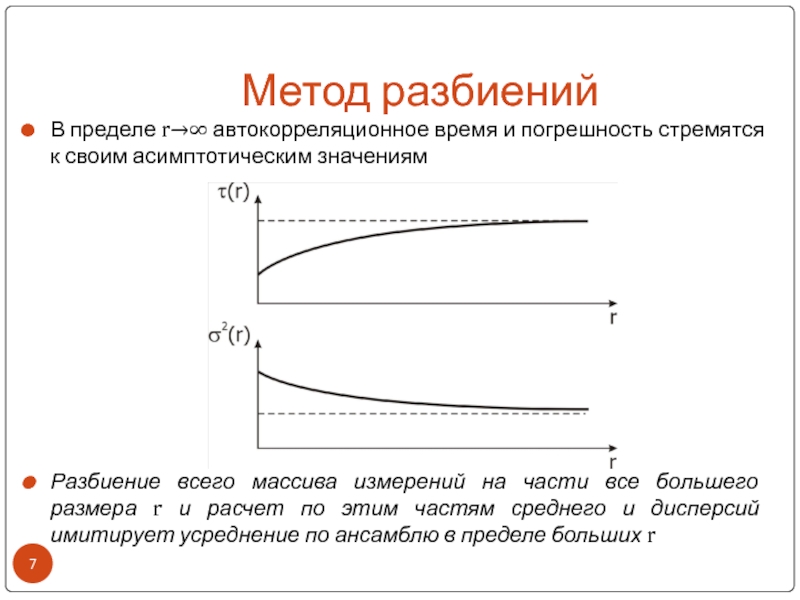
В пределе r→∞ автокорреляционное время и погрешность стремятся к
своим асимптотическим значениям
Разбиение всего массива измерений на части все большего
размера r и расчет по этим частям среднего и дисперсий имитирует усреднение по ансамблю в пределе больших r
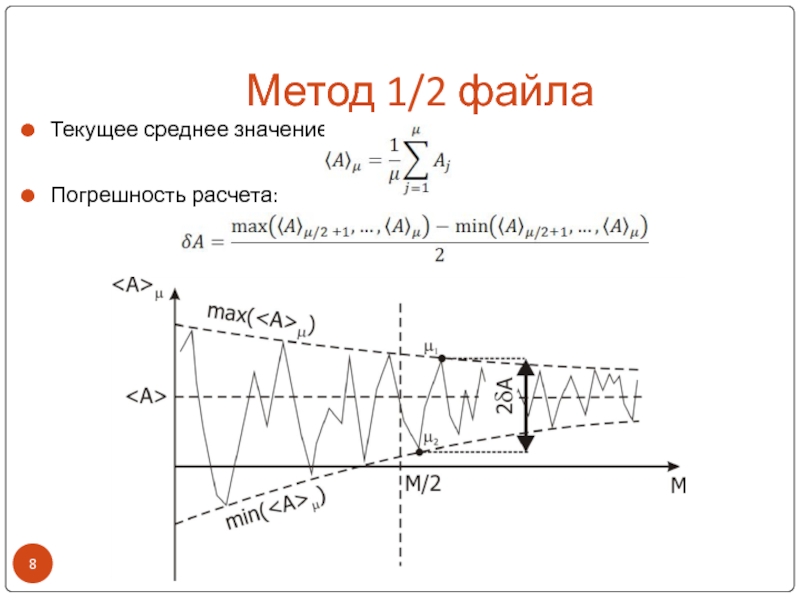
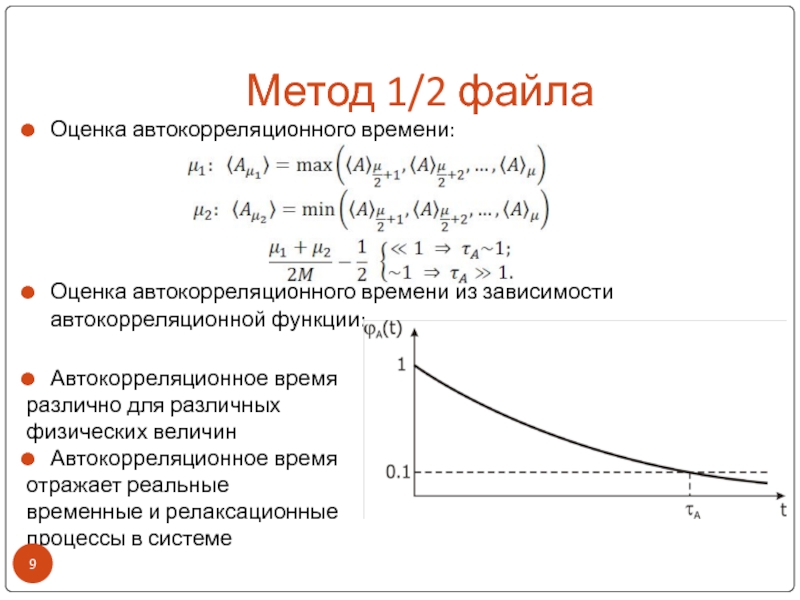
Слайд 9Метод 1/2 файла
Оценка автокорреляционного времени:
Оценка автокорреляционного времени из зависимости автокорреляционной
функции:
Автокорреляционное время
различно для различных
физических величин
Автокорреляционное время
отражает реальные
временные и релаксационные
процессы в
системе
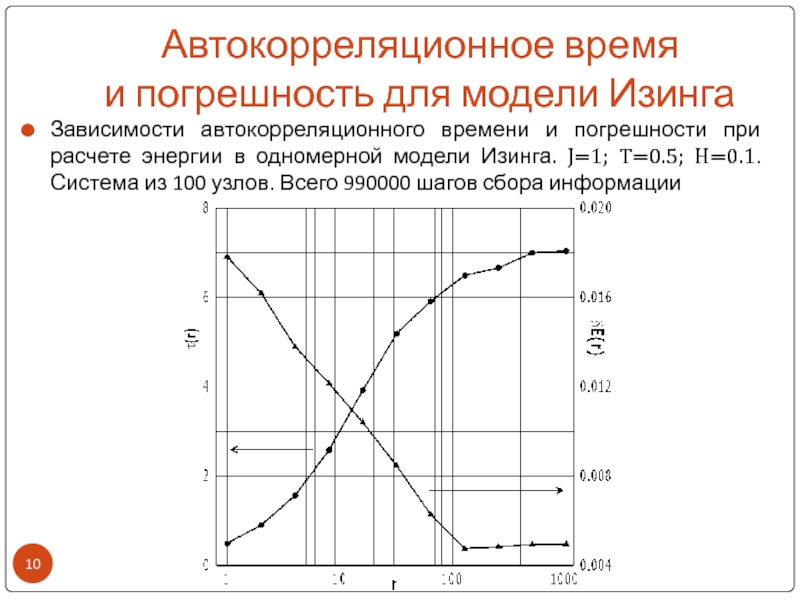
Слайд 10Автокорреляционное время
и погрешность для модели Изинга
Зависимости автокорреляционного времени и погрешности
при расчете энергии в одномерной модели Изинга. J=1; T=0.5; H=0.1.
Система из 100 узлов. Всего 990000 шагов сбора информации