РАСЧЁТ ТРЁХШАРНИРНЫХ СИСТЕМ

шарнирами *)
*) как правило, цилиндрическими
Два типа трёхшарнирных систем (ТШС)


Распорные

ТШС
( один из трёх дисков – «земля» )

ТШС с затяжкой

D3 = «з е м л я»

D1

D2

A

B

C

A, B – опорные шарниры
С – ключевой шарнир

D1

D2

A

C

B

D3

З а т я ж к а
( диск без связей с «землёй» )

D

K

VA

VB

H

H

H – распор

Трёхшарнирная арка

Трёхшарнирная рама

A

A

В

В

С

С

A

В

С

D

K

D

С

В

A

Трёхшарнирные
арка рама
с затяжками

A

В

С

Трёхшарнирная система
с дисками-фермами

стержнями,
обращёнными, как правило,
выпуклостью навстречу
действующей нагрузке.
Т р ё

х ш а р н и р н ы е а р к и

A

B

C

l

Вершина арки

f

ymax

l – длина пролёта
ymax – стрела подъёма

f – расстояние от ключевого шарнира
до линии опорных шарниров

В случае ключевого шарнира в вершине арки f = ymax

По очертанию оси

Круговая

Параболическая

Эллиптическая

Стрельчатая

По расположению опор

С опорами на одном уровне

Δh

С опорами на разных уровнях

По относительной
высоте

– пологие
( f / l < 1/8…1/10)

– подъёмистые
( f / l > 1/4…1/3)

Трёхшарнирной рамой
называется трёхшарнирная система, два основных диска
которой являются ломаными или прямолинейными стержнями.

с т в е н н ы й а

н а л и з:
П = 0; С = 0 W = 3D – ( 2H + C0 )

D1

D2

A

B

C

D1

D2

A

B

D3

D

K

A

A

В

В

С

С

D

С

В

A

D = 2; H = 1; C0 = 4 W = 0

D = 3; H = 3; C0 = 3 W = 0

C

б) с т р у к т у р н ы й а н а л и з:
общее требование: шарниры А, В, С не должны лежать на одной прямой

1. Р а с п о р н ы е Т Ш С

2. Т Ш С с з а т я ж к о й

с т в е н н ы й а

н а л и з:
П = 0; С = 0 W = 3D – ( 2H + C0 )

1. Р а с п о р н ы е Т Ш С

2. Т Ш С с з а т я ж к о й

D1

D2

A

B

C

D1

D2

A

B

D3

D

K

A

В

D

С

В

A

D = 2; H = 1; C0 = 4 W = 0

D = 3; H = 3; C0 = 3 W = 0

C

б) с т р у к т у р н ы й а н а л и з:
при наличии поступательных шарниров

С

A

В

С

γ

γ = 0 !

K

γ

о р н ы е Т Ш С



D1
D2
A
B
C












Вариант 1
(

общая система уравнений равновесия )

D1

A

VA

HA

HC

VC

C

D2

B

C

VB

HC

VC

HB

y

x

0

Искомые реакции связей:
VA , HA , VB , HB , VC , HC

Уравнения равновесия дисков:

( VA , HA , VC , HC )

( VВ , HВ , VC , HC )

Вариант 2
( рациональный способ определения реакций )

D1

D2

C

A

VA

HA

B

VB

HB

y

x

α0

Шаг 1: уравнения равновесия системы в целом:

l

Частный случай – вертикальная нагрузка

о р н ы е Т Ш С
Вариант 1
(

общая система уравнений равновесия )

D1

A

VA

HA

HC

VC

C

D2

B

C

VB

HC

VC

HB

y

x

0

Искомые реакции связей:
VA , HA , VB , HB , VC , HC

Уравнения равновесия дисков:

( VA , HA , VC , HC )

( VВ , HВ , VC , HC )

Вариант 2
( рациональный способ определения реакций )

D1

D2

C

A

B

y

x

α0

Шаг 1: уравнения равновесия системы в целом:

l

Частный случай – вертикальная нагрузка

D1

A

Шаг 2: уравнения равновесия одного из дисков:

HC

VC

C

a

VC

HC

о р н ы е Т Ш С
Вариант 2
(

рациональный способ определения реакций )

D1

D2

C

A

B

y

x

α0

Шаг 1: уравнения равновесия системы в целом:

l

Частный случай – вертикальная нагрузка

D1

A

Шаг 2: уравнения равновесия одного из дисков:

HC

VC

C

a

VC

HC

Переход к ортогональным составляющим
опорных реакций:

B

x

α0

A

y

HA

VA

HB

VB

Алгоритм определения реакций по варианту 2:

1. Реакции опор раскладываются на составляющие –
вертикальные и по направлению линии АВ.

2. Записываются уравнения равновесия системы
в целом ( моментов относительно точек А и В
и проекций на ось х ), из которых находятся
вертикальные реакции опор А и В.

3. Система разделяется сечением по ключевому
шарниру на два диска ( обязательная операция ! ).
Для любого из дисков записывается уравнение
равновесия моментов относительно точки С,
из которого находится реакция ( или ).

4. Из уравнения Σ x = 0 для всей системы
определяется реакция ( ).

о р н ы е Т Ш С
Вариант 2
(

рациональный способ определения реакций )

D1

D2

C

A

B

y

x

α0

Шаг 1: уравнения равновесия системы в целом:

l

D1

A

Шаг 2: уравнения равновесия одного из дисков:

HC

VC

C

a

VC

HC

Особые случаи распорных ТШС,
для которых целесообразно изменение
порядка расчёта в сравнении
с общим алгоритмом

Рациональный приём:
В первую очередь рассматривается
равновесие диска, которому принадлежат шарниры, расположенные на одной вертикали ( горизонтали )
и находится реакция НА ( НВ ); затем используются
уравнения равновесия системы в целом.

Общий признак:
ключевой шарнир С располагается
на одной вертикали ( или горизонтали )
с одним из опорных шарниров.

А

А

В

В

С

С

VА

VА

VB

VB

HB

HB

HA

HA

HB

VA

VB

HA

HA

HB

VB

VA

с з а т я ж к о й





D1
D2
A




B






D3
D
K
C



Вариант 1
Формирование

и решение системы уравнений равновесия дисков D1 , D2 и D3 ( по 3 уравнения
для каждого диска – всего 9 уравнений ) с девятью
неизвестными реакциями внешних и внутренних связей – VA , HA , VB , HB , VC , HC , VD , HD , RK

Вариант 2
( рациональный способ определения реакций связей )

Шаг 1
Уравнения
равновесия
системы в целом:

y

x

HD

VD

RK

VD

Шаг 2
Уравнения равновесия затяжки ( D3 ):

A

B

x3

α0

l3

Шаг 3
Уравнения равновесия
одного из дисков ( D1 или D2 ):

D2

K

C

RK

B

HC

VC

VC

HC

Частные случаи:

1. Вертикальные нагрузки на затяжке

2. Незагруженная затяжка

3. Прямолинейная незагруженная затяжка:

с з а т я ж к о й





D1
D2
A



B





D
K
C



Трёхшарнирная система

с прямолинейной незагруженной затяжкой

Рациональный способ
определения реакций связей

Шаг 1
Уравнения
равновесия
системы в целом:

y

x

HD

VD

RK

VD

Шаг 2
Уравнения равновесия затяжки ( D3 ):

x3

α0

Шаг 3
Уравнения равновесия
одного из дисков ( D1 или D2 ):

D2

K

C

RK

B

HC

VC

VC

HC

hR

Продольная сила в прямолинейной незагруженной затяжке:

bR

A

B

с з а т я ж к о й





D1
D2
A



B





D
K
C



Трёхшарнирная система

с прямолинейной незагруженной затяжкой

Рациональный способ
определения реакций связей

Шаг 1
Уравнения
равновесия
системы в целом:

y

x

HD

VD

RK

VD

Шаг 2
Разделение системы сечением I – I
по ключевому шарниру и затяжке
( стандартный приём )

Шаг 3
Уравнения равновесия
одного из дисков ( D1 или D2 ):

D2

K

C

RK

B

HC

VC

VC

HC

hR

Продольная сила в прямолинейной незагруженной затяжке:

bR

I

I

N3

е в о п р о с ы
( в

скобках даны номера слайдов, на которых можно найти ответы на вопросы;
для перехода к слайду с ответом можно сделать щелчок мышью по номеру в скобках*);
для возврата к контрольным вопросам сделать щелчок правой кнопкой мыши
и выбрать «Перейти к слайду 14» )
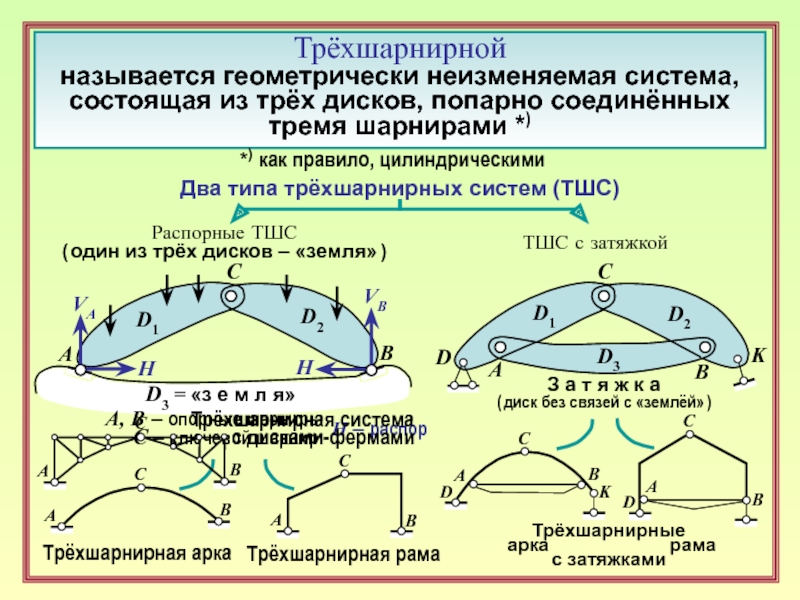
1. Что такое трёхшарнирная система? ( 2 )
2. Основные типы трёхшарнирных систем. ( 2 )
3. Что такое распор? ( 2 )
4. Что такое затяжка? ( 2 )
5. Разновидности распорных трёхшарнирных систем. ( 2 )
6. Разновидности трёхшарнирных систем с затяжкой. ( 2 )
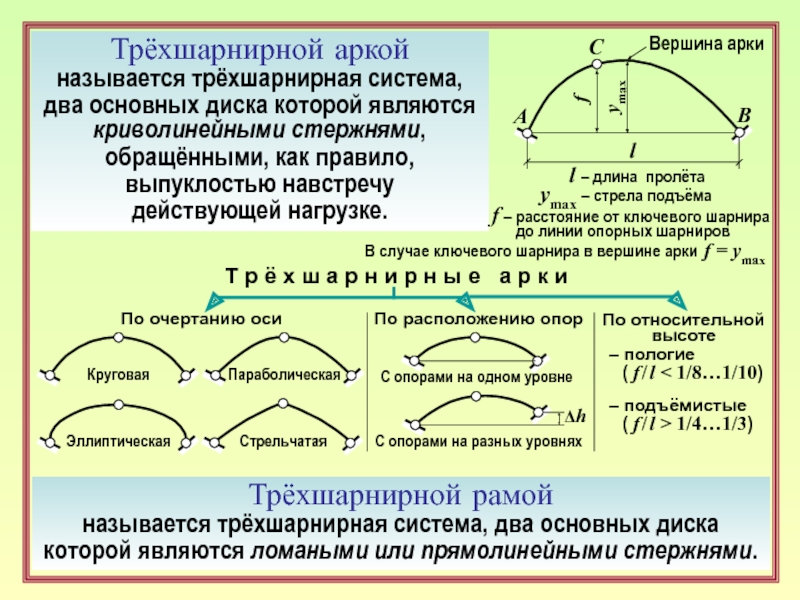
7. Что такое трёхшарнирная арка? Как классифицируются трёхшарнирные арки? ( 3 )
8. Что такое трёхшарнирная рама? ( 3 )
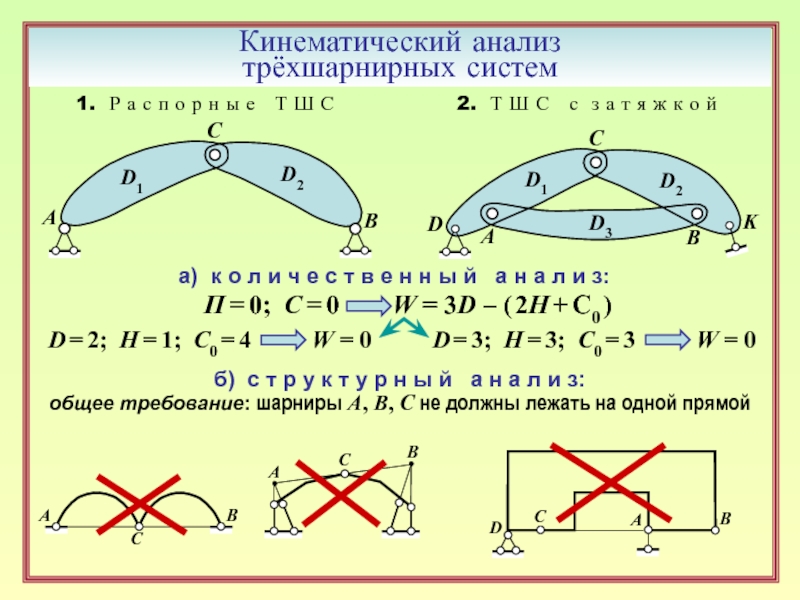
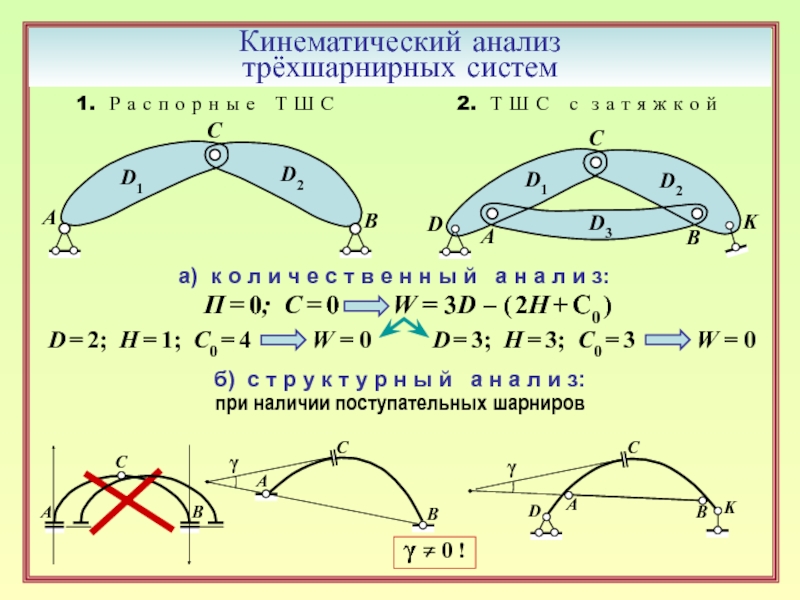
9. Кинематический анализ трёхшарнирных систем разных типов. ( 4 )
10. Требования к расположению связей в трёхшарнирных системах. ( 4, 5 )
11. Можно ли в вершине арки с опорными цилиндрическими шарнирами на одном уровне
поставить вертикальный поступательный шарнир? ( 5 )
12. Можно ли в трёхшарнирной системе выделить главную и второстепенную части?
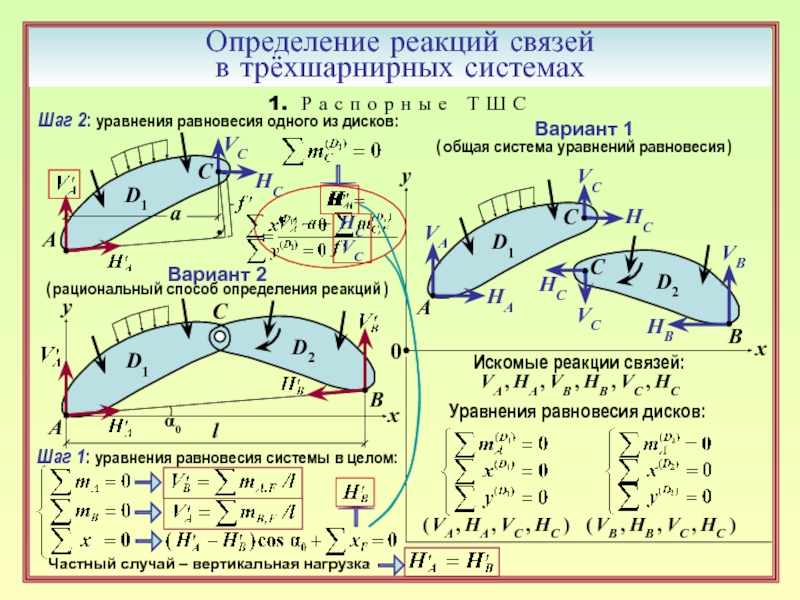
13. Порядок определения реакций связей в трёхшарнирной распорной системе. ( 6 – 8 )
14. От чего зависит распор трёхшарнирной системы? ( 7 )
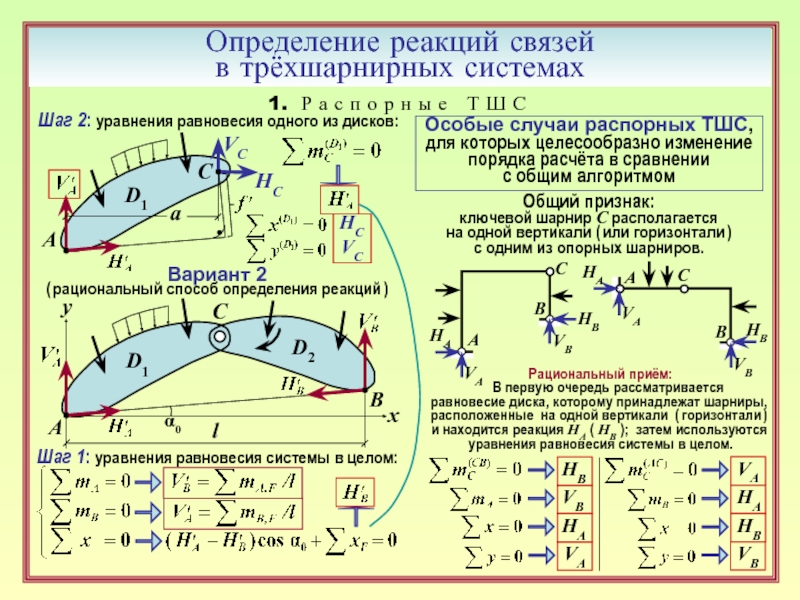
15. Рациональный порядок определения реакций связей в трёхшарнирной системе
при расположении ключевого и одного из опорных шарниров на одной вертикали
(или горизонтали). ( 9 )
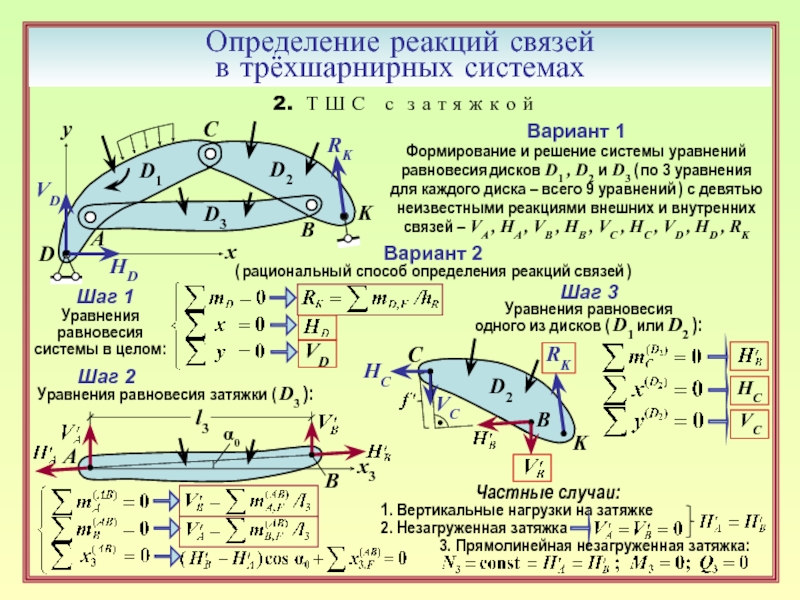
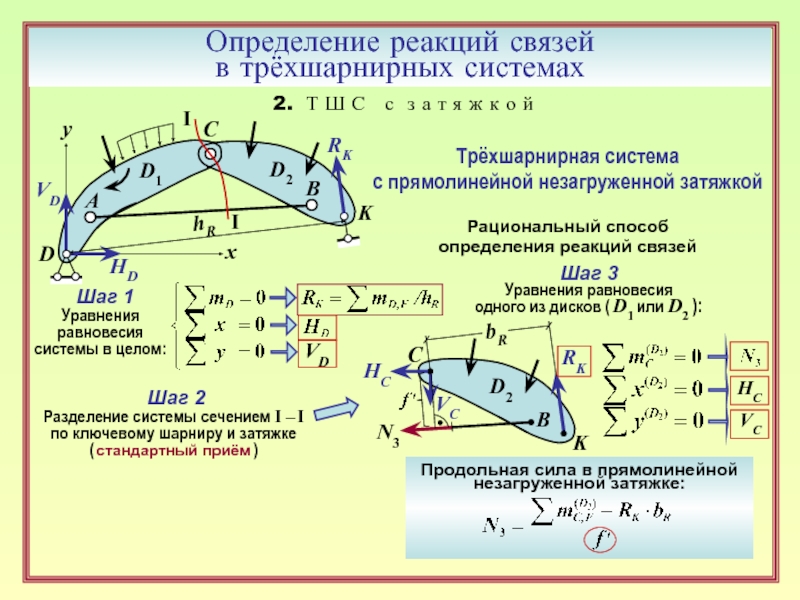
16. Порядок определения реакций связей в трёхшарнирной системе с затяжкой. ( 10 )
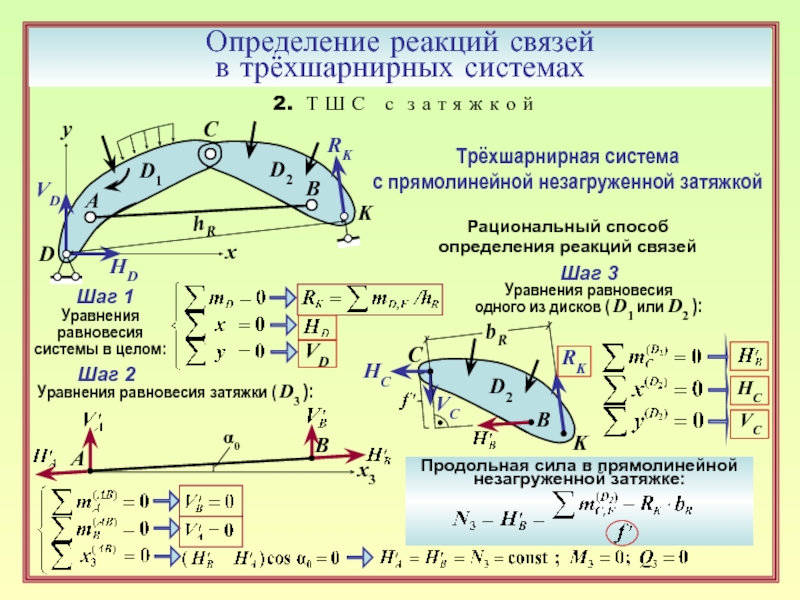
17. Каков характер работы незагруженной прямолинейной затяжки? ( 10, 11 )
18. Как определяется продольная сила в прямолинейной незагруженной затяжке? ( 11 )
19. Стандартный приём определения продольной силы в прямолинейной затяжке
трёхшарнирной системы. ( 12 )
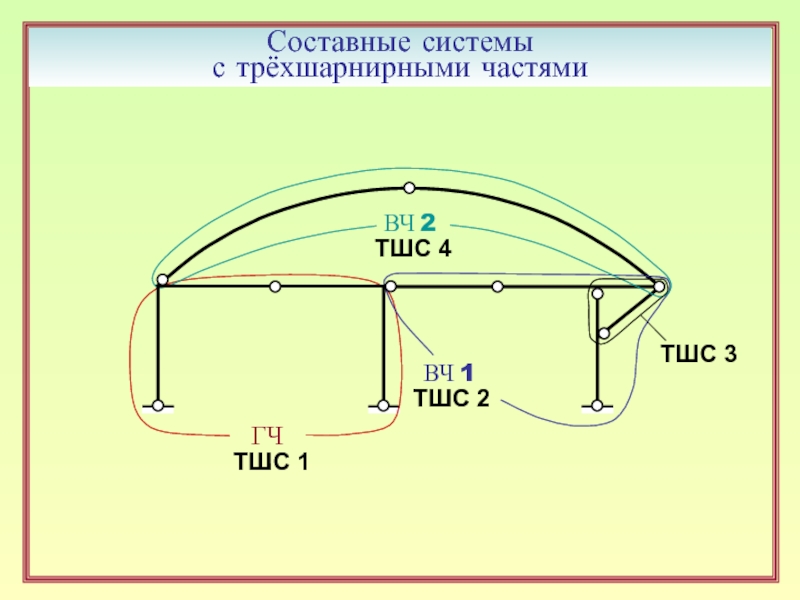
20. Порядок расчёта составных систем с трёхшарнирными частями. ( 13 )
____________________________________________________________
*) Только в режиме «Показ слайдов»