Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Расчёт погрешностей результатов экспериментов
Содержание
- 1. Расчёт погрешностей результатов экспериментов
- 2. Измерительные приборы
- 3. Измерительные приборы
- 4. Приборная погрешностьAпр – цена наименьшего деления (ЦНД)
- 5. Aпр = 0,1 гAпр = 100 ВПриборная
- 6. Повторные измеренияРезультаты измерений величины A в одинаковых
- 7. Погрешность результата ? Среднеквадратичное отклонение (стандартный разброс) среднего значения(3)(4)
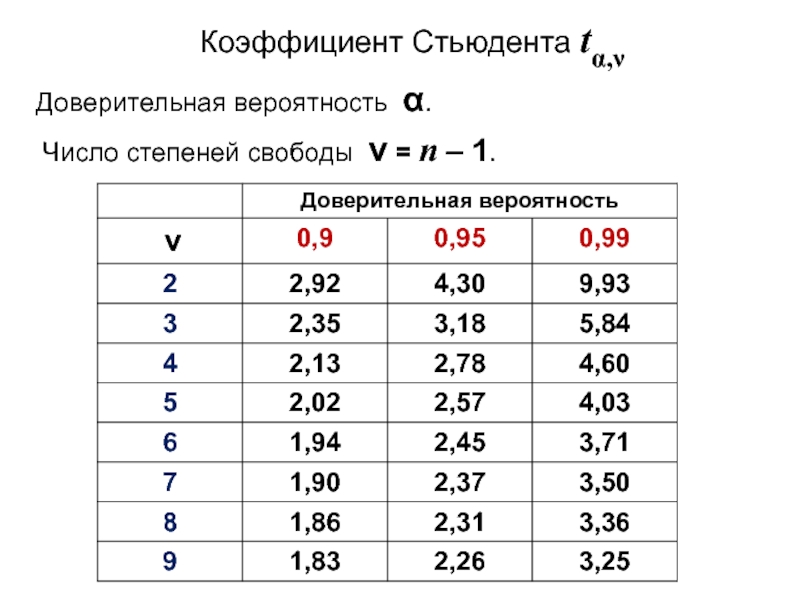
- 8. Доверительная вероятность . Число степеней свободы = n – 1.Коэффициент Стьюдента t,
- 9. Случайная погрешность(5)(6)Абсолютная погрешностьОтносительная погрешность(7)
- 10. Косвенные измеренияПример 1: Измерение жесткости пружиныНепосредственно измеряется:1)
- 11. Косвенные измеренияПример 2: Измерение ускорения свободного паденияНепосредственно
- 12. Косвенные измеренияНаилучшее приближенное значениегде средние значения вычисляются по формуле (1):(8)(9)
- 13. Погрешности косвенных измеренийАбсолютная погрешностьОтносительная погрешность(11)(10)
- 14. Частный случай 1.Величина Z является суммой или
- 15. Пример 3: Измерение суммарной массы двух грузов
- 16. Частный случай 2.Величина Z является произведением или
- 17. Пример 1: Измерение жесткости пружиныЖесткость: k =
- 18. Частный случай 3.Величина Z является степенью измеряемой величины AZ = APАбсолютная погрешность:Относительная погрешность(15)
- 19. Пример 4: Измерение объёма шараНепосредственно измеряется диаметр шара dЧисло можно задать с требуемой точностью
- 20. Значащие цифры числаВсе верные цифры, начиная с
- 21. Значащие цифры размерных величинКоличество значащих цифр не
- 22. Значащие цифры при действиях с числамиСложение1,36 +
- 23. Количество верных значащих цифр в результате не
- 24. Линейная аппроксимацияФункция вида y = k x
- 25. В эксперименте измеряется N пар числовых значений:
- 26. Абсолютная погрешность коэффициента:
- 27. Скачать презентанцию
Измерительные приборы
Слайды и текст этой презентации
Слайд 5Aпр = 0,1 г
Aпр = 100 В
Приборная погрешность
Aпр – цена
наименьшего деления (ЦНД)
или единица младшего разряда.
Aпр = 2 мА
Aпр
= 0,05 А
Слайд 6Повторные измерения
Результаты измерений величины A в одинаковых условиях:
a1, a2,
..., аi, ...,an ; где n — число измерений
Среднее статистическое:
Наилучшее приближение измеряемой величины:
(1)
(2)
Слайд 7Погрешность результата ?
Среднеквадратичное отклонение (стандартный разброс)
среднего значения
(3)
(4)
Слайд 10Косвенные измерения
Пример 1: Измерение жесткости пружины
Непосредственно измеряется:
1) удлинение пружины L
2)
масса подвешенного груза m
Жесткость: k = mg / L
A,
B, C, … - непосредственно измеряемые величины.(8)
Погрешностями величин L
и m являются приборные погрешности.
Слайд 11Косвенные измерения
Пример 2: Измерение ускорения свободного падения
Непосредственно измеряется:
1) высота, с
которой падает тело h
2) время падения тела t
Ускорение свободного
падения: g = 2h / t2Время падения t измеряется несколько раз, вычисляется среднее и среднеквадратичное отклонение, абсолютная случайная погрешность t.
Слайд 12Косвенные измерения
Наилучшее приближенное значение
где средние значения вычисляются по формуле (1):
(8)
(9)
Слайд 14Частный случай 1.
Величина Z является суммой или разностью непосредственно измеряемых
величин A и B
Z = A + B
или Z = A – B Абсолютная погрешность:
Относительные погрешности
(12)
Слайд 15Пример 3: Измерение суммарной массы двух грузов
m = m1
+ m2
Непосредственно измеряются массы:
m1 и m2
Абсолютная погрешность суммарной массы :
m1
и m2 - абсолютные погрешности масс m1 и m2
Слайд 16Частный случай 2.
Величина Z является произведением или отношением непосредственно измеряемых
величин A и B
Z = AB или Z
= A/B Абсолютная погрешность:
Относительная погрешность
(13)
(14)
Слайд 17Пример 1: Измерение жесткости пружины
Жесткость: k = mg / L
Относительная
погрешность жесткости
Абсолютная погрешность:
m, g, - относительные погрешности
массы m, ускорения свободного падения g, удлинения пружины L.За погрешность g берём погрешность округления.
Слайд 18Частный случай 3.
Величина Z является степенью измеряемой величины A
Z =
AP
Абсолютная погрешность:
Относительная погрешность
(15)
Слайд 19Пример 4: Измерение объёма шара
Непосредственно измеряется
диаметр шара d
Число
можно задать с требуемой точностью
Слайд 20Значащие цифры числа
Все верные цифры, начиная с первой ненулевой слева.
25 ; 0,0187 ; 41,300 ; 0,000460
Погрешность числа не превышает
единицы последнего (младшего) разряда среди значащих цифр. 1 ; 0,0001 ; 0,01 ; 0,000001
Слайд 21Значащие цифры размерных величин
Количество значащих цифр не зависит от единицы
измерения.
25 мм = 0,025 м = 25000 мкм =
0,25 см Значащие цифры отмечены красным цветом.
Слайд 22Значащие цифры при действиях с числами
Сложение
1,36 + 0,354 = 1,714
1,71
Умножение
2,8 12,3 = 34,44 34
Слайд 23Количество верных значащих цифр в результате не может быть больше,
чем максимальное количество значащих цифр в исходных данных.
Количество верных
значащих цифр в результате может стать равным минимальному числу значащих цифр в исходных данных. После вычисления на калькуляторе или на компьютере результат требуется округлить до допустимого количество значащих цифр.
Слайд 24Линейная аппроксимация
Функция вида y = k x , где k
– постоянный коэффициент.
Пример: Закон Ома для участка цепи.
I = U/R
Необходимо
найти коэффициент k.
Слайд 25В эксперименте измеряется N пар числовых значений:
xk , yk
; k = 1, … N .
Наилучшее приближение коэффициента:
