РАСПОЛОЖЕНИЕ ПРЯМОЙ И ПЛОСКОСТИ

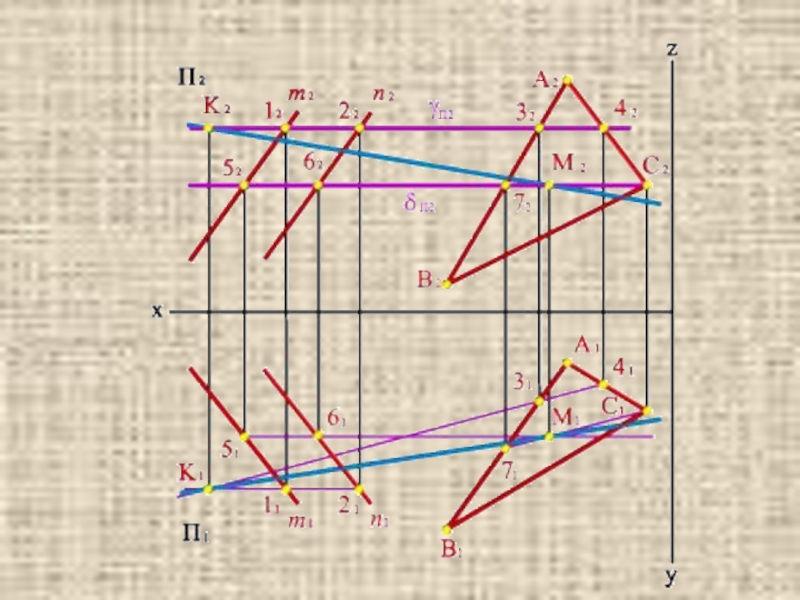
плоскостей
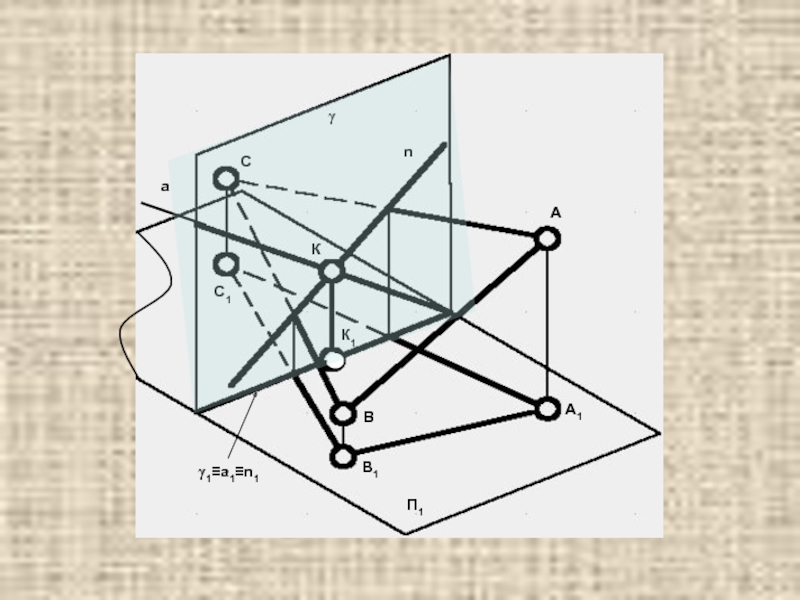
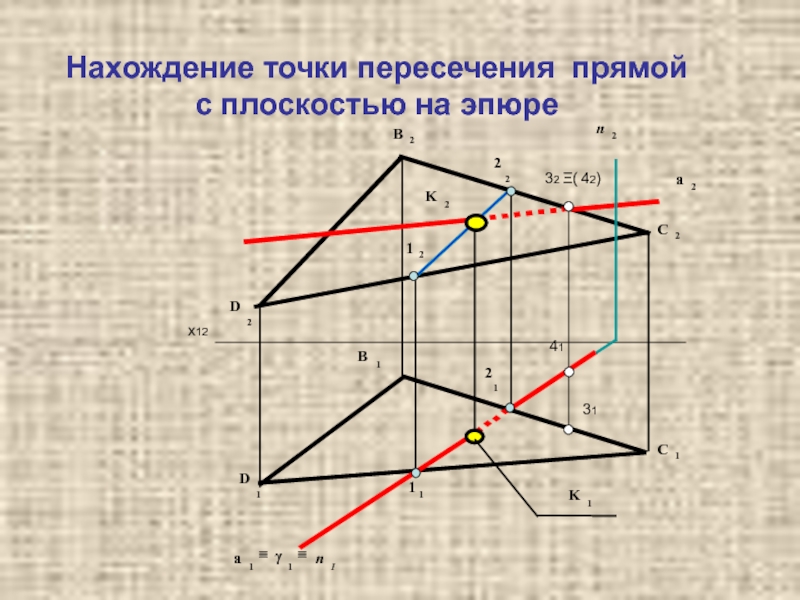
1.2 Пересечение прямой с плоскостью
1.3 Прямая линия параллельная плоскости

1.4 Прямая линия перпендикулярная плоскости
1.5 Взаимно параллельные плоскости
1.6 Взаимно перпендикулярные плоскости
2. Вопросы для самопроверки.

лежит в плоскости;
прямая пересекает плоскость;
прямая параллельна плоскости.

Прием определения взаимного

положения прямой и плоскости заключается в следующем:
через данную прямую проводят вспомогательную плоскость и строят линию пересечения этой плоскости и данной плоскости;
устанавливают взаимное положение данной прямой и прямой пересечения плоскостей; найденное положение определяет взаимное положение данных прямой и плоскости.

Для построения линии пересечения плоскостей необходимо найти две общие для

них точки.
При решении задач на построение линии пересечения плоскостей применяют способ вспомогательных плоскостей.

а и плоскости α

и видимость прямой по отношению к плоскости

след вспомогательной горизонтально проецирующей плоскости γ, тогда а∈γ.
2. Горизонтальный след

плоскости γ1 пересекает проекцию плоскости В1С1D1 в точках 11 и 21, которые определяют положение горизонтальной проекции n1- линии пересечения плоскостей γ и Δ ВСD. Для нахождения фронтальной проекции n2 проведем линии связи до пересечения с одноименными сторонами (ΔBCD), получим проекции точек 12 и 22.

плоскости γ , в пересечении их фронтальных проекций определяется фронтальная

проекция точки К2, принадлежащей и прямой а и плоскости ΔВСD. По линии связи находим горизонтальную проекцию точки К1.
4. Методом конкурирующих точек определяем видимость прямой а по отношению к плоскости ΔВСD. Точки 3 и 4 являются фронтально конкурирующими. Точка 3 находится ближе к наблюдателю и дальше от плоскости П2, на фронтальной проекции она перекрывает 42, а К232 будет невидима, т.к. 4 Є а.

этой плоскости.

двум пересекающимся прямым этой плоскости.
Теорема
Прямая линия перпендикулярна плоскости,

если ее проекции перпендикулярны одноименным проекциям направлений горизонтали и фронтали плоскости.

плоскости соответственно параллельны двум
прямым другой

плоскости, то эти плоскости
параллельны.

из плоскостей имеет прямую линию, перпендикулярную к другой плоскости.

пространстве прямая линия и плоскость?
Как относительно друг друга могут быть

расположены в пространстве две плоскости?
Каков алгоритм решения на комплексном чертеже задач на пересечение?