Равнопеременное движение Движение твердого тела

касательное ускорение не изменяется по величине.
Запишем выражение для касательного ускорения

через проекцию скорости:

Полученное выражение есть дифференциальное уравнение, которое легко решается разделением переменных и интегрированием левой
и правой частей:

В свою очередь скорость точки также связывается с дуговой координатой дифференциальной зависимостью:

После подстановки
выражения для скорости
и интегрирования получаем :

скорость точки
при равнопеременном движении

дуговая координата
точки при равно-
переменном движении

Классификация движений точки.

используется для получения новых зависимостей и формул.
Существует пять видов движения

твердого тела:
1. Поступательное (ползун, поршень насоса, спарник колес паровоза, движущегося по прямолинейному пути, кабина лифта, дверь купе, кабина колеса обозрения).
2. Вращательное (маховик, кривошип, коромысло, колесо обозрения, обычная дверь).
3. Плоскопараллельное или плоское (шатун, колесо локомотива при качении по прямолинейному рельсу, шлифовальный круг).
4. Сферическое (гироскоп, шаровая стойка).
5. Общий случай движения или свободный полет (пуля, камень, небесное тело)

Поступательное движение твердого тела – такое движение при котором любая прямая, жестко связанная с телом, остается параллельной самой себе. Обычно поступательное движение отождествляется с прямолинейным движением его точек, однако это не так. Точки и само тело (центр масс тела) могут двигаться по криволинейным траекториям, см. например, движение кабины колеса обозрения.

Теорема о поступательном движении твердого тела – При поступательном движении твердого тела все его точки описывают тождественные траектории и имеют в каждый момент времени геометрически равные скорости и ускорения.

C

Проведем радиус-векторы к двум точкам A и B, а также соединим эти точки вектором rBA.

В любой момент времени выполняется векторное равенство:

В любой момент времени вектор rBA остается постоянным по направлению
(по определению поступательного движения) и по величине
(расстояние между точками не изменяется). Отсюда:
и это означает, что в каждый момент времени положение точки A отличается от положения
точки B на одну и ту же величину rBA = const, т.е. траектории этих двух точек тождественны
(совпадают друг с другом при наложении).

Продифференцируем по времени левую и правую часть соотношения:

и это означает, что в каждый момент времени скорость точки A равна геометрически
(т.е. векторно) скорости точки B.

Второе дифференцирование по времени приводит к соотношению:

и это означает, что в каждый момент времени ускорение точки A равно геометрически
(т.е. векторно) ускорению точки B.

Таким образом, поступательное движение твердого тела полностью определяется
движением одной точки, принадлежащей этому телу и выбранной произвольным образом.
Все параметры движения этой точки (траектория, скорость и ускорение) описываются
уравнениями и соотношениями кинематики точки.

точки можно получить общие аналитические выражения для этой скорости через

координаты рассматриваемой точки при произвольной расположении оси вращения в пространстве:

Отсюда получаются аналитические формулы для проекций скоростей точки:

Преобразования вращательных движений – изменение величины и направление угловых скоростей вращающихся звеньев в различных передаточных механизмах:
Фрикционное зацепление:

Скорости входящих в контакт точек колес при отсутствии проскальзывания равны:

Отсюда:

Передаточное число, характеризующее изменение скорости вращения при передаче вращения от одного звена к другому – отношение угловой скорости ведущего колеса
к угловой скорости ведомого:

Зубчатое зацепление – число зубьев каждого из колес прямо пропорционально
радиусу колеса. Окружные скорости входящих в контакт точек поверхностей зубьев по-прежнему равны. Полученные соотношения остаются справедливыми, в том числе и для случая внутреннего зацепления.

Радиусы делительных окружностей связаны с шагом зубьев соотношениями:
С использованием чисел зубьев каждого из колес имеем:

Ременная и цепная передачи –. Окружные скорости
входящих в контакт с ремнем или цепью точек поверхностей
обоих колес или зубьев этих колес по-прежнему равны (ремень или цепь не растягиваются и не сжимаются).
Полученные соотношения остаются справедливыми.

тела движется в в плоскости параллельной некоторой неподвижной плоскости. Сечение

тела одной из таких плоскостей есть плоская фигура, остающаяся в этой плоскости при движении тела.

Теорема о плоскопараллельном движении твердого тела – плоскопаралллельное движение твердого тела однозначным образом определяется движением плоской фигуры, образованной сечением тела одной из параллельных плоскостей.
Выберем две точки на произвольных двух сечениях тела, находящиеся на одном перпендикуляре к этим плоскостям:

Проведем к каждой точке радиусы-векторы из неподвижной точки O и свяжем их между собой вектором
M1M2:

При плоском движении тела вектор M1M2 не изменяется по величине, остается параллельным самому себе (движется поступательно) и, следовательно, точки этого вектора описывают тождественные траектории и имеют в каждый момент времени одинаковые скорости и ускорения:

Таким образом, при плоском движении тела движение каждой точки одной из плоских фигур определяет движение соответствующих точек,
находящихся во всех других смежных параллельных плоскостях.

Следствие: Поскольку положение плоской фигуры однозначно определяется положением ее двух точек или отрезка прямой, проведенной через эти точки, то плоскопараллельное движение твердого тела определяется движением прямолинейного отрезка, принадлежащего одному из сечений тела параллельными плоскостями.

Разложение плоскопараллельного движения плоской фигуры на поступательное и вращательное движения – Плоскую фигуру или отрезок прямой можно перевести из одного положения в другое бесчисленным множеством способов, меняя последовательность выполнения поступательного и вращательного движения между собой, а также выбирая различные траектории и точки в качестве полюса:

Таким образом, плоскопараллельное движение состоит из двух движений: поступательное и вращательное, и его всегда можно разложить на эти два движения. При этом поступательное зависит от выбора полюса и траектории движения, а вращательное, характеризуемое поворотом вокруг выбранного полюса, не зависит от выбора полюса (для любого полюса величина угла поворота и направление вращения – одинаковы).

A

B

B1

A2

B2

A1

Уравнение движения плоской фигуры: Выбирая в качестве полюса любую точку, например, A, поступательная часть движения будет описываться уравнениями движения этой точки. Вращательная часть движения описывается уравнением изменения угла поворота вокруг полюса:

Уравнения движения любой точки плоской фигуры, положение
которой задается координатами локальной системы отсчета, связанной с фигурой:

полюса – Выберем два произвольных прямолинейных отрезка, изображающих положение плоской

фигуры и два полюса на этих отрезках:

Углы наклона отрезков к горизонтальной оси различны и связаны между собой соотношением:

Продифференцируем это соотношение:

Отсюда следует, что угловые скорости двух отрезков равны:

После повторного дифференцирования следует,
что угловые ускорения двух отрезков также равны:

Таким образом, угловая скорость и угловое ускорение
плоской фигуры не зависят от выбора полюса и их можно представить в виде векторов, перпендикулярных плоскости фигуры:

Теорема о сложении скоростей – Скорость любой точки плоской фигуры равна геометрической сумме скоростей полюса и вращательной скорости этой точки вокруг полюса.

Радиусы-векторы точек A и B связаны между собой соотношением:

Продифференцируем это соотношение:

Второе слагаемое есть вращательная
скорость точки B вокруг полюса A:

Таким образом, скорость точки B равна геометрической сумме скорости полюса A и вращательной скорости точки B вокруг полюса :

Следствие 1 – Проекции скоростей точек плоской фигуры на ось,
проходящую через эти точки равны .

x1

Спроецируем векторное соотношение на ось x1:

Следствие 2 – Концы векторов скоростей точек плоской фигуры, лежащих на одной прямой, также
лежат на одной прямой и делят эту прямую на отрезки пропорциональные расстояниям между точками.

Концы векторов вращательных скоростей точек B и A лежат на одной прямой и делят ее на отрезки
пропорциональные расстояниям между точками:

Концы векторов скоростей полюса A лежат, изображенных
в точках B и C также лежат на одной прямой.

неподвижной во время движения. Остальные точки движутся по сферическим поверхностям,

центры которых совпадают с неподвижной точкой.
Углы Эйлера – используются для описания сферического движения твердого тела посредством ввода двух системы координат:

x

y

z

J







Oxyz – неподвижная система координат с началом в неподвижной точке,
O - подвижная система координат, жестко связанная с телом, с началом в той же точке.

O

Положение подвижной системы координат может быть однозначно задано тремя углами:
 - угол поворота системы O вокруг оси z – угол прецессии;

2) θ – угол поворота системы O вокруг нового положения горизонтальной оси x (OJ) – угол нутации;

φ - угол поворота системы O вокруг нового положения вертикальной оси z (O) – угол собственного
вращения.

Уравнения сферического движения твердого тела:

Теорема Эйлера – Твердое тело, имеющее одну неподвижную точку, можно переместить
из одного положения в другое одним поворотом вокруг некоторой оси, проходящей через эту точку.

O

Рассмотрим дугу большого круга AB, находящейся на сферической поверхности.
Дуга большого круга – дуга наименьшей кривизны на поверхности (часть окружности,
полученной сечением плоскости, проходящей через центр). Далее будет
подразумеваться, что все дуги есть дуги большого круга.

Пусть AB переместилась в положение A1B1. Проведем дуги AA1 и ВB1.

Из середин С и D дуг AA1 и ВB1 проведем дуги, перпендикулярные к дугам AA1 и ВB1.

Точка пересечения дуг CO1 и DO1 является неподвижной и определяет положение оси
вращения. Эту точку соединим дугами с концами дуг AA1 и ВB1.

Полученные криволинейные треугольники AO1B и A1O1B1 равны по равенству сторон и
углы  AO1B =  A1O1B1.

Если к каждому из этих углов добавить один и тот же  BO1A1, то полученные углы
 AO1A1 и  BO1B1 будут также равны между собой и будут являться углом поворота всех
точек тела вокруг оси OO1.

Точки A и B при перемещении в положение A1, B1, в общем случае движутся не обязательно по дугам большого круга. За малый промежуток
времени t переход точек из одного положения в другое происходит поворотом тела вокруг некоторой оси вращения на угол φ. При
устремлении t 0 ось вращения занимает предельное положение и называется мгновенной осью вращения тела в данный момент.

мгновенной оси вращения, модуль которого равен:

Угловое

ускорение сферического движения твердого тела – характеризует изменение вектора
угловой скорости:



среднее угловое ускорение
в интервале времени t,

Угловое ускорение в момент времени t:

Вектор угловой скорости с началом в неподвижной точке при движении тела изменяется
подобно радиусу-вектору точки, движущейся в пространстве по некоторой траектории.
Вектор скорости этой точки направлен по касательной к траектории и определяется выражением:

Траектория конца вектора угловой скорости с началом в неподвижной точке при движении тела
описывает кривую, называемую годографом вектора угловой скорости.

E

Сравнивая выражения для вектора углового ускорения тела и вектора скорости точки можно установить, что
угловое ускорение тела геометрически равно линейной скорости конца вектора угловой скорости.
Прямая, по которой направлен вектор углового ускорения, называется осью мгновенного углового ускорения (E).

Скорость точки твердого тела при сферическом движении – определяется как вращательная скорость
вокруг мгновенной оси:

Мгновенная ось вращения в данное мгновение – геометрическое место точек
с нулевой скоростью.
Уравнение мгновенной оси получается приравниванием проекций скоростей нулю:

x

Проекции скоростей на подвижные оси , ,  имеют аналогичный вид.

Проекции скоростей
(формулы Эйлера):

Ускорение точки твердого тела при сферическом движении:

- Ускорение точки равно геометрической сумме вращательного ускорения относительно оси мгновенного углового ускорения (E) и осестремительного ускорения относительно мгновенной оси вращения ().

Модуль вращательного ускорения равен: , где hE – длина перпендикуляра, опущенного
на ось мгновенного ускорения E.
Вектор вращательного ускорения направлен перпендикулярно радиусу вращения (hE) в сторону дуговой стрелки
углового ускорения.

Модуль осестремительного ускорения равен: , где h – длина перпендикуляра, опущенного
на мгновенную ось вращения  .
Вектор осестремительного ускорения направлен по радиусу вращения (h) к мгновенной оси вращения.

Модуль полного ускорения равен:

однозначно определяется положением трех его точек, не лежащих на одной

прямой. По трем точкам можно построить треугольник, который и будет далее представлять тело в пространстве.
Разложение движения свободного твердого тела – Как и в случае плоского движения существует бесчисленное множество способов представления движения свободного тела в виде совокупности двух, более простых движений. Например, можно перевести тело из исходного положение, обозначенное треугольником ABC, в другое положение, соответствующее треугольнику A1B1C1, поступательным перемещением в положение A1B’C’, а затем поворотом его вокруг некоторой оси, проходящей через точку, выбранной в качестве полюса, например, точку A1:

A

B

C

A1

B’

C’



Или, напротив, вначале повернуть треугольник ABC вокруг некоторой
оси, проходящей через точку, выбранной в качестве полюса, например,
точку A, чтобы стороны треугольника ABC стали параллельными
сторонам треугольника A1B1C1, а затем перевести треугольник AB’C
поступательным движением в положение A1B1C1:

A

B

C

C’

B’

Таким образом, движение свободного тела можно представить как
совокупность поступательного движения и сферического движения
вокруг некоторой точки, принадлежащей телу, выбранной в качестве
полюса:

Уравнения движения
свободного тела:

Скорость точки свободного тела – Скорость любой точки тела
равна геометрической сумме скорости полюса и скорости этой точки
в ее сферическом движении вокруг полюса.

Радиусы-векторы точек A и B связаны между
собой соотношением:

Продифференцируем это соотношение:

Второе слагаемое есть скорость точки B
во сферическом движении вокруг полюса A:

x



Полученное соотношение полностью совпадает с теоремой о сложении скоростей для плоского движения. Разница состоит лишь в том, что используется не центр вращения, а ось мгновенного вращения .
Отсюда имеют место и аналогично доказываются следствия о равенстве проекций скоростей точек на ось, проходящих через эти точки, и о пропорциональности отрезков линии, проходящей через концы векторов скоростей.

В дополнение к этим двум следствиям из теоремы о сложении
вытекает третье следствие:
Скорости точек свободного тела, лежащих на прямой,
параллельной мгновенной оси, геометрически равны.
Справедливость утверждения следует из равенства скоростей
этих точек во вращении вокруг мгновенной оси.

h

одновременно в двух или нескольких движениях.
Примеры сложного движения точки (тела):

лодка, переплывающая реку; человек, идущий по движущемуся эскалатору; камень подвижной кулисы, поршень качающегося цилиндра; шары центробежного регулятора Уатта.
Для описания сложного движения точки или для представления движения в виде сложного используются
неподвижная система отсчета O1, связанная с каким-либо условно неподвижным телом, например, с Землей, и
подвижная система отсчета Oxyz, связанная с каким-либо движущимся телом.

Абсолютное движение ( a ) - движение точки, рассматриваемое относительно неподвижной системы
отсчета. Относительное движение ( r ) - движение точки, рассматриваемое относительно подвижной
системы отсчета.
Переносное движение ( e ) - движение подвижной системы отсчета, рассматриваемое относительно
неподвижной системы отсчета.

Абсолютная скорость (ускорение) точки va ( aa ) - скорость (ускорение) точки, вычисленная относительно
неподвижной системы отсчета.
Относительная скорость (ускорение) точки vr ( ar ) – скорость (ускорение) точки, вычисленная относительно
подвижной системы отсчета.
Переносная скорость (ускорение) точки ve ( ae ) – скорость (ускорение) точки,
принадлежащей подвижной системе координат или твердому телу, с которым жестко связана подвижная
система координат,
совпадающей с рассматриваемой движущейся точкой в данный момент времени и
вычисленная относительно неподвижной системы отсчета.

Теорема о сложении скоростей – абсолютная скорость точки равна геометрической сумме относительной и переносной скоростей точки.
В любой момент времени справедливо соотношение:

Продифференцируем это соотношение по времени имея в виду, орты i, j, k изменяют свое направление в общем случае движения
свободного тела, с которым связана подвижная система координат:

Здесь первое слагаемое (vO) - скорость полюса O;
следующие три – относительная скорость точки (vr).

Для последних трех слагаемых следует определить
производные по времени от ортов i, j, k:

Здесь использована векторная формула для
линейной скорости точки относительно оси вращения:

Подставим векторные произведения
в последние три слагаемые:

Сумма первого и последнего слагаемого – скорость точки свободного тела есть переносная скорость точки (ve):

Таким образом, с учетом того, что
производная по времени радиуса-вектора 
есть абсолютная скорость, получаем:

Модуль вектора
абсолютной скорости:

абсолютное ускорение точки равно геометрической сумме относительного,
переносного и кориолисова ускорений

точки.
Было получено ранее соотношение для скорости:

Продифференцируем это соотношение
по времени еще раз:

Здесь первое слагаемое (aO) - ускорение полюса O;
следующие три – относительное ускорение точки (ar).

Для последних трех слагаемых
следует определить вторые производные по времени
от ортов подвижной системы
координат i, j, k:

Подставим эти выражения
в последние три слагаемые
и сгруппируем:

Сумма первого и полученных
двух слагаемых – ускорение
точки свободного тела есть
переносное
ускорение точки (ae):

В оставшихся шести слагаемых сложим одинаковые члены, подставим векторные произведения для первых производных по времени от ортов и сгруппируем:

Полученная компонента ускорения представляет собой кориолисово ускорение (ac):

Таким образом, с учетом того, что вторая производная по времени
радиуса-вектора  есть абсолютное ускорение, получаем:

■ Величина и направление ускорения Кориолиса:
Модуль вектора кориолисова ускорения:
Ускорение Кориолиса обращается в ноль
в двух случаях:
Угловая скорость переносного движения равна 0 (поступательное
переносное движение).
Вектор угловой скорости параллелен вектору относительной
скорости (синус угла между векторами обращается в 0).

Направление вектора
кориолисова ускорения:
Определяется по одному
из трех правил:
По определению векторного
Произведения .
По правилу правой руки .
По правилу Жуковского:

Спроецировать вектор относительной скорости
на плоскость, перпендикулярную вектору угловой скорости.

б) Повернуть проекцию вектора относительной скорости
на прямой угол в сторону дуговой стрелки угловой скорости.

Кориолиса было выведено группировкой слагаемых произведений,
содержащих проекции относительной скорости и

производные по времени от ортов подвижной системы координат. При этом ранее было получено
удвоенное число таких слагаемых.
Для прояснения физических причин возникновения ускорения Кориолиса рассмотрим качественный пример, в котором специально будем
полагать постоянными вектор относительной скорости (в подвижной системе координат) и вектор угловой переносной скорости (вращения
подвижной системы координат относительно неподвижной оси):

Пусть в некоторый момент времени положение точки и вектора относительной и переносной скоростей таковы, как они изображены на
рисунке (вид сверху):

Через некоторое время точка удалится от оси вращения и тело повернется
на некоторый угол.
В результате:
относительная скорость изменится по направлению из-за наличия переносной угловой скорости и
переносная линейная скорость изменится по величине из-за наличия относительной скорости, изменяющей расстояние точки до оси вращения.

Таким образом, можно считать что существует две причины возникновения
ускорения Кориолиса:
1) переносная угловая скорость влияет на относительную скорость, a
2) относительная скорость в свою очередь влияет на переносную линейную скорость. Возможно, это поможет запомнить коэффициент, равный двум, в формуле,
определяющей ускорение Кориолиса.

■ Примеры определения направления ускорения Кориолиса
удобно рассмотреть для случаев различного положения движущихся
точек по поверхности Земли, вращающейся относительно своей оси:

при котором тело участвует одновременно в двух или нескольких движениях.
Все

определения, касающиеся составляющих движения, данные для сложного движения точки, остаются справедливыми для твердых тел.
Кинематика сложного движения точки используется здесь для получения новых соотношений, описывающих сложное движение твердого тела.
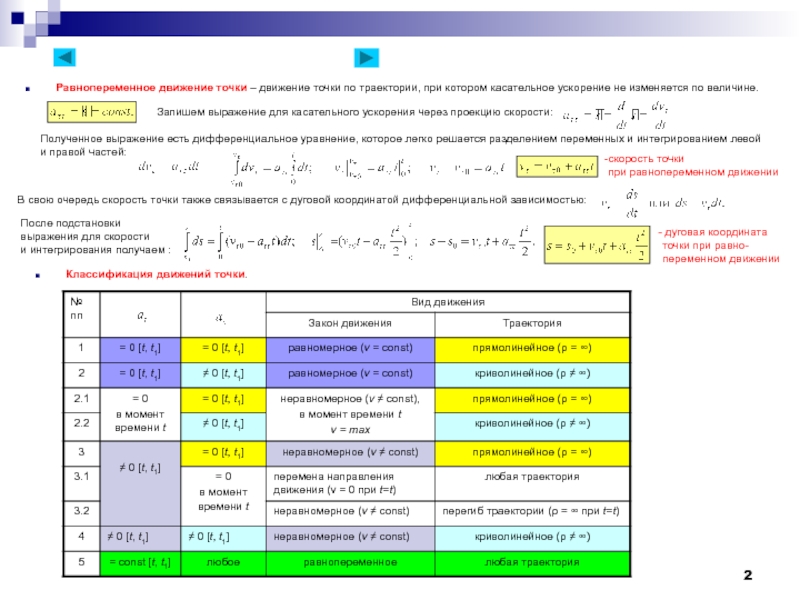
■ Сложение поступательных движений твердого тела – При поступательных движениях все точки твердого тела имеют одинаковые
скорости, что позволяет использовать теорему о сложении скоростей точки для сложного движения:
Таким образом, абсолютная скорость тела, равная скорости одной из точек этого тела,
равна геометрической сумме переносной и относительной скоростей этого тела.

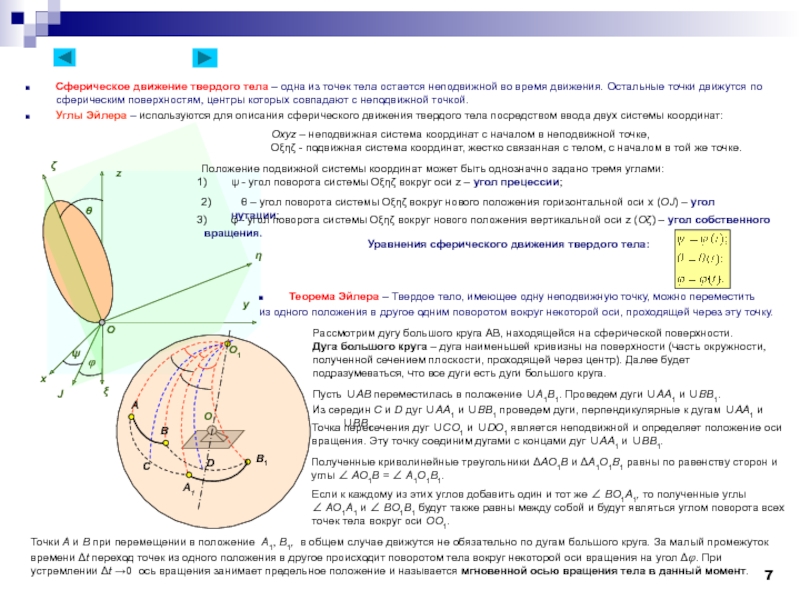
■ Сложение вращательных движений твердого тела – здесь рассмотрим два случая различного положения осей вращения:
оси вращений параллельны и оси вращений пересекаются.
■ Оси вращений параллельны – диск вращается относительно своей оси, проходящей через точку O1, с угловой скоростью r, ось диска
движется по круговой траектории вокруг оси, проходящей через неподвижную точку O, с угловой скоростью e:

Произвольная точка A, принадлежащая диску, совершает сложное движение (движется по круговой
траектории в подвижной плоскости, жестко связанной с кривошипом OO1) и абсолютная скорость
этой точки определяется выражением:

Задачу определения скоростей любой из точек диска можно упростить, если найти положение мгновенного центра вращения (точку, скорость которой в данный момент равна нулю):

Отсюда:

Это означает, что точка K лежит на отрезке
прямой OO1 и делит его на части, обратно
пропорциональные угловым скоростям:

Для определения абсолютной угловой скорости рассмотрим точку O1, которая не участвует в относительном движении, и определим ее скорость дважды (в переносном движении и в абсолютном движении). Эти скорости должны быть одинаковы:

Представим отрезок OO1, как сумму отрезков и отрезок OK выразим через O1K:

Отсюда:

В случае противоположных по направлению вращений можно показать, деление отрезка OO1будет происходить так же обратно пропорционально угловым скоростям, но только внешним образом (точка K будет лежать на этой же линии вне отрезка OO1 со стороны большего вектора угловой скорости). Тогда: и абсолютная угловая скорость будет равна разности скоростей:

Оба соотношения можно объединить одним векторным соотношением:

Таким образом, абсолютная угловая скорость равна
геометрической сумме относительной и переносной
угловых скоростей.
Имеется полная аналогия между сложением векторов
угловых скоростей и сложением двух параллельных сил.
При сложении таких сил равнодействующая приложена
в точке, делящей расстояние между силами на отрезки,
обратно пропорциональные силам.

24

сил, равных по величине и противоположно направленных между собой
равнодействующая этих

сил обращается в ноль (система таких сил не приводится к равнодействующей) и эти силы образуют качественно
новую простейшую систему, называемой парой сил. При этом действие пары сил характеризуется моментом пары.
Совершенно аналогично при сложении двух параллельных векторов угловых скоростей, равных по величине и противоположно направленных
между собой, называемых парой вращений, результирующая угловая скорость обращается в ноль. В результате получается поступательное
движение, скорость которого определяется величиной момента пары вращений:

d

Таким образом, два вращения с угловыми скоростями, равными
по величине и противоположными по направлению, могут быть
заменены одним поступательным движением.
Точно также возможна и обратная процедура – представление
поступательного движения в виде пары вращений.

■ Сложение вращательных движений твердого тела
в случае пересечения осей вращений – тело вращается с угловой скоростью r относительно своей оси, проходящей через точку пересечения с другой осью вращения O. Относительно второй оси первая ось вращается с угловой скоростью e:

Вектор скорости поступательного движения твердого тела является
свободным вектором (может перемещаться параллельно самому себе)
в то время как векторы угловой скорости являются скользящими
векторами, которые могут перемещаться только по линии действия.

Поскольку точка пересечения осей вращения имеет нулевую скорость, то принимая ее за неподвижную точку
в пространстве, вычислим скорость произвольной точки M по теореме о сложении скоростей:

Векторная сумма угловых скоростей, полученная в скобках, представляет собой результирующую угловую
скорость, определяющую единственное вращение тела вокруг некоторой мгновенной оси (см. сферическое
движение), которая может рассматриваться как абсолютная угловая скорость:

Таким образом, абсолютная угловая скорость равна геометрической сумме относительной и переносной
угловых скоростей :

При сложении вращательных движений более двух результирующий вектор угловой скорости равен
геометрической сумме векторов всех угловых скоростей, участвующих в сложном движении:

тела – пусть тело участвует во вращательном движении с угловой
скоростью

ω и поступательном движении со скоростью v. Угол  между векторами угловой скорости и поступательной скорости произвольный.

Разложим вектор скорости поступательного движения на два взаимно перпендикулярных
вектора так, чтобы один совпал с вектором угловой скорости:

O

Вектор скорости v1 представим в виде пары вращений
с угловыми скоростями, равными заданной угловой скорости
вращательного движения:

A

Вектор оставшейся поступательной скорости v* , как свободный вектор перенесем в точку A, а два вектора
угловых скоростей, изображенные в точке O, можно удалить, поскольку они равны по величине, направлены
по одной прямой в противоположные стороны:

Расстояние OA находится
из равенства скорости
моменту пары вращений:

Таким образом, получили вращение с заданной угловой скоростью ω вокруг оси, проходящей через точку A,
и поступательное движение со скоростью v*. Такая комбинация более не может быть упрощена и представляет
собой кинематический винт, реализующий винтовое движение твердого тела. Ось, проходящая через точку A,
вдоль которой направлен вектор угловой скорости, называется мгновенной винтовой осью.

■ Скорость точки твердого тела при винтовом движении – пусть тело участвует во вращательном движении с угловой скоростью ω1 ,
которое примем за относительное движение, и поступательном движении со скоростью v*, которое примем за переносное движение.

A

M

Абсолютная скорость точки M:

Точка M движется по спиральной траектории делая один оборот за время T:

За время T точка М перемещается по направлению переносной скорости на величину h (шаг винта):

Отношение поступательной скорости с угловой скорости
является характеристикой винтового движения и
называется параметром винта:

С использованием параметра
винта шаг винта:

Модуль абсолютной скорости точки M с использованием параметра винта:

В частном случае, при  =900 (вектор поступательной скорости перпендикулярен вектору угловой скорости)
движение приводится к одному вращению вокруг оси, проходящей через точку A:

26

– пусть тело участвует в n вращательных движениях и m

поступательных движениях.

Выберем полюс A и приложим в этой точке вектора угловых скоростей:

A

Получили совокупность и совокупность
пар вращений векторов угловых скоростей,
пересекающихся
в одной точке.

Совокупность вращений можно
заменить одним вращением:

Каждую пару вращений можно
заменить одним поступательным
движением:

Всю совокупность поступательных движений можно заменить сложением одним поступательным движением:

Получаем в общем случае одно вращение с угловой скоростью ω* вокруг оси, проходящей через полюс A, и поступательное движение со скоростью vA( A – точка приведения), что приводит к кинематическому винту, рассмотренному выше.

Угловая скорость ω* не зависит от выбора полюса и это есть первый (векторный) инвариант:

Скорость поступательного движения зависит от выбора полюса, но существует скалярная величина, связанная с поступательной скоростью, инвариантная к выбору полюса. Запишем теорему о сложении скоростей, связывающую линейные (поступательные) скорости, вычисленные относительно различных точек приведения:

Умножим обе части равенства скалярно на вектор угловой скорости:

Второе слагаемое в правой части равно нулю, т.к. вращательная скорость
перпендикулярна вектору угловой скорости. Следовательно, скалярные
произведения векторов поступательных скоростей, вычисленных для различных
точек приведения, и вектора угловой скорости равны:

- второй (скалярный) инвариант.

Раскрывая скалярные произведения получаем:
откуда:

- минимальная поступательная скорость.

Итак, угловые скорости в кинематике складываются так же, как силы в статике (эти векторы являются скользящими векторами).
Поступательные скорости в кинематике складываются так же, как моменты пар в статике (эти векторы являются свободными векторами).
Все способы преобразования сил и пар сил в статике подобны преобразованиям скоростей твердого тела в кинематике.
И в статике, и в кинематике при приведении системы в общем случае получается статический винт (динама), и соответственно кинематический винт. Как в статике, так и в кинематике существуют соответствующие инвариантные величины (помечены звездочками) и их производные (главный минимальный момент и минимальная поступательная скорость).