Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
РАВНОВЕСНЫЕ ЭЛЕКТРОХИМИЧЕСКИЕ СИСТЕМЫ
Содержание
- 1. РАВНОВЕСНЫЕ ЭЛЕКТРОХИМИЧЕСКИЕ СИСТЕМЫ
- 2. Теория возникновения электродного потенциала Нернста
- 3. 2. Химическая теория ЭДС (1857 г. Де-ля-Рив),
- 4. Нернст получил качественную картину возникновения скачка потенциала
- 5. При равновесии
- 6. Теория Нернста имела ряд недостатков: физический смысл
- 7. Работы Писаржевского и ИзгарышеваТеория электродного потенциала, учитывающая
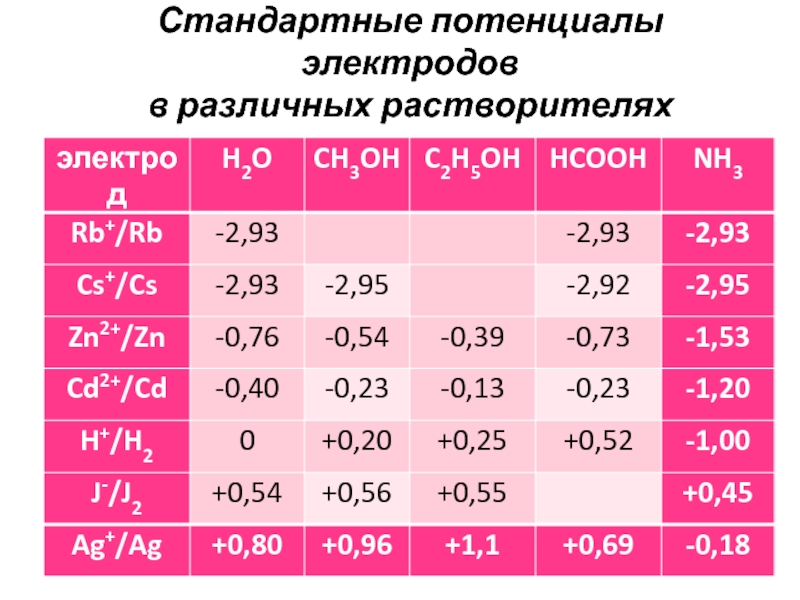
- 8. Стандартные потенциалы электродов в различных растворителях
- 9. Установлено, что изменение электродного потенциала при переходе
- 10. Указанные качественные представления Писаржевского о влиянии энергии
- 11. Квантово-механическая теория электродного потенциалаКоличественные расчеты электродного потенциала,
- 12. Термодинамический вывод уравнения для обратимой ЭДС и
- 13. G =
- 14. Выразим значение потенциала
- 15. Расшифруем уравнение (*):Первое и второе
- 16. Скачать презентанцию
Слайды и текст этой презентации
Слайд 2
Теория возникновения электродного потенциала Нернста
1. Физическая или «контактная» теория итальянского
Слайд 32. Химическая теория ЭДС (1857 г. Де-ля-Рив), согласно которой источником
электрической энергии являются химические реакции на границе металл-раствор.
Химическая теория
ЭДС наиболее полно развита в работах Нернста и Оствальда в конце 19 века (1890 г.).Теория Нернста получила название осмотической теории. Она основывается на трех принципах:
Электродный потенциал является скачком потенциала на границе металл-раствор, а ЭДС равна алгебраической сумме электродных потенциалов.
Электродный потенциал возникает в результате обмена ионами между металлом и электролитом.
Движущими силами обмена являются осмотическое давление растворенного вещества (π) и электролитическая упругость растворения металла (р).
То есть теория Нернста отвечала на вопрос где и почему возникает скачок потенциалов.
Слайд 4Нернст получил качественную картину возникновения скачка потенциала на границе металл-раствор
и вывел количественную зависимость величины этого скачка от состава раствора.
Он рассмотрел три возможных случая при контакте между металлом и раствором, содержащим ионы металла.Если осмотическое давление раствора π больше электролитической упругости растворения р – в этом случае ионы из раствора переходят на металл.
Если р > π – металл растворяется.
Если р = π – переходы равновероятны.
Ионы – частицы заряженные, поэтому их преимущественный переход в одну какую-либо фазу приведет к возникновению заряда поверхности, а следовательно и скачка потенциала. Возникший скачок потенциала тормозит преимущественный переход ионов, так что, в конце концов, переходы в обоих направлениях будут равновероятны, а значение скачка потенциала будет равновесным.
Слайд 5При равновесии
= - zFε
Отсюда
Если С = 1, то
Поскольку
полагалось, что к растворам применимы законы идеальных газов, то – стандартный потенциал, зависящий от природы металла и от температуры.
уравнение Нернста для электродного потенциала.
Слайд 6Теория Нернста имела ряд недостатков:
физический смысл стандартного потенциала не
ясен, поскольку не ясен смысл электролитической упругости растворения металла (р).
Рассчитанная из формулы стандартного потенциала она могла принимать значения от 10-20 до 1040.стандартный потенциал является функцией только природы металла и не зависит от природы растворителя. На практике была установлена зависимость ε0 от природы растворителя. В связи с этими недостатками возникла необходимость в пересмотре физических предпосылок теории.
Слайд 7Работы Писаржевского и Изгарышева
Теория электродного потенциала, учитывающая взаимодействие ионов с
растворителем (сольватацию) была развита Писаржевским в 1912-14 г.
M =
Mz+ + zeMz+ + xL = MLxz+
По Писаржевскому переход ионов металла в раствор совершается не за счет неясной электролитической упругости растворения, а за счет энергии взаимодействия ионов металла с растворителем. Следовательно, этот переход зависит не только от природы металла, но и от природы растворителя. Экспериментальные данные подтвердили этот вывод.
Слайд 9Установлено, что изменение электродного потенциала при переходе от одного растворителя
к другому тем больше, чем меньше радиус и больше заряд
иона, т.е. чем сильнее проявляется энергия взаимодействия иона с растворителем. Наоборот, потенциалы электродов, где в установлении равновесия участвуют крупные малозарядные ионы, меняются мало, например, потенциалы цезиевого, рубидиевого, йодного электродов.При переходе от одного растворителя к другому меняется не только величина потенциала, но и порядок расположения электродов в таблице стандартных потенциалов. Из таблицы так же видно, что можно составить элемент из одинаковых электродов, но в разных растворителях и получить значительную величину ЭДС.
Слайд 10Указанные качественные представления Писаржевского о влиянии энергии сольватации на электродный
потенциал в 1926-28 гг. были развиты Изгарышевым.
По Изгарышеву при
переходе ионов из раствора в металл ионы теряют свою гидратную оболочку (необходим учет энергии гидратации).Адсорбированные молекулы воды или другого растворителя взаимодействуют с ионами кристаллической решетки и при определенных условиях вырывают их, образуя гидратированные ионы (необходим учет прочности связи ионов металла в кристаллической решетке).
Изгарышев показал, что на основании его теории можно рассчитывать электродные потенциалы, однако строгих количественных расчетов им сделано не было.
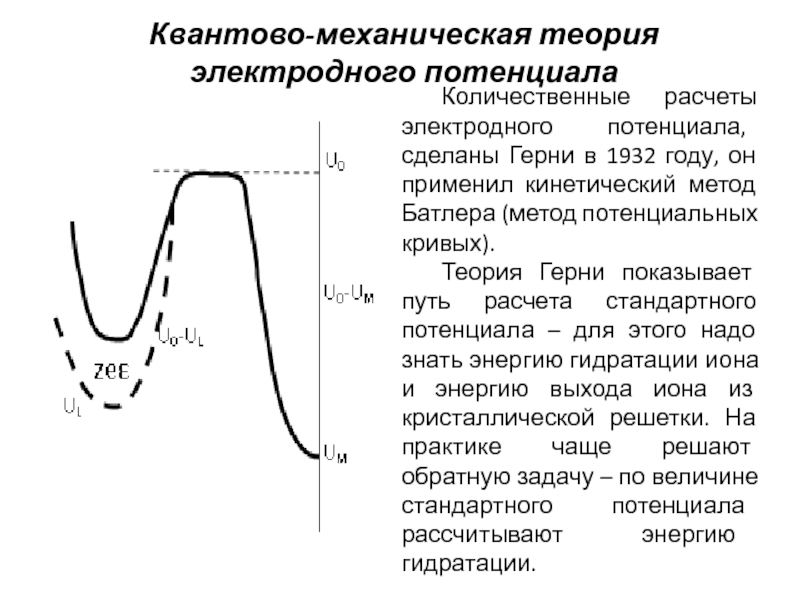
Слайд 11Квантово-механическая теория электродного потенциала
Количественные расчеты электродного потенциала, сделаны Герни в
1932 году, он применил кинетический метод Батлера (метод потенциальных кривых).
Теория Герни показывает путь расчета стандартного потенциала – для этого надо знать энергию гидратации иона и энергию выхода иона из кристаллической решетки. На практике чаще решают обратную задачу – по величине стандартного потенциала рассчитывают энергию гидратации.
Слайд 12Термодинамический вывод уравнения для обратимой ЭДС и равновесного электродного потенциала
1878
г Гиббс и в 1882 г Гельмгольц развили представление о
химической теории ЭДС, ими был дан термодинамический вывод этой теории.В электрохимической системе обратимо при постоянной температуре и давлении протекает реакция:
νАА + νВВ + …± ze ↔ νCC + νDD +….
∆G = Wmax= - zFE
Изменение свободной энергии системы равно максимальной полезной работе – в данном случае – электрической.
Слайд 13 G = ∑νi μi ,
где i > 0 для конечных веществ и i
0 для начальных веществ.∆G = ∑νкон μкон - ∑νнач μнач
μi = μi0 + RT lnai
∆G = ∑νi μi0 + RT ∑νilnai
Если П ai = 1, то ∆G = ∑νi μi0 = ∆G0
∆G = ∆G0 + RT
При достижении равновесия ∆G = 0, а активности - равновесные. ∆G0 = - RT ln Kр.
∆G = - RT ln Kр + RT ∑νilnai.
- zFE = - RT ln Kр + RT νi ln Пai
С другой стороны изменение свободной энергии системы определяется изменением химического потенциала:
Слайд 14Выразим значение потенциала
Е
=
(*)Если активности всех участников реакции равны 1, то
Е = RT/zF ln Kр = Е0.
Е = Е0
Основная особенность электрохимической реакции – пространственное разделение токообразующих реакций.
νАА + ze ↔ νCC К1=
νВВ - ze ↔ νDD К2=