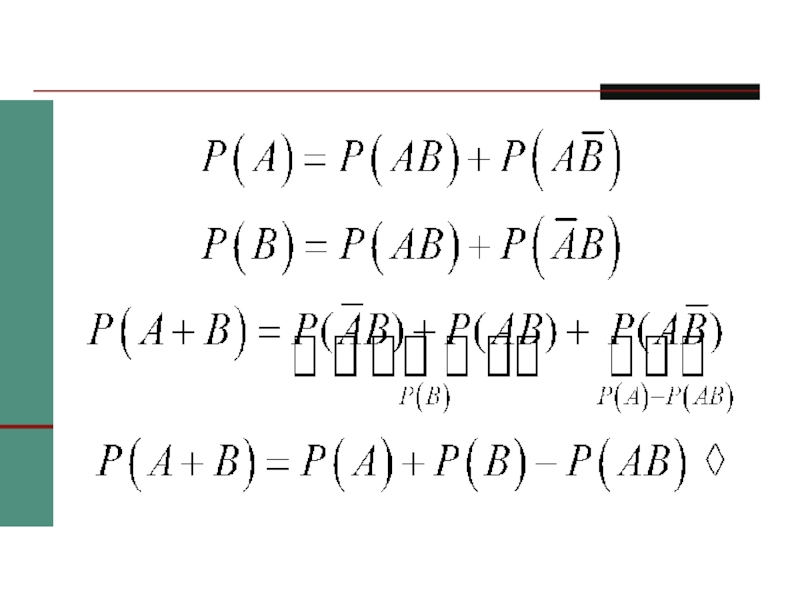Слайд 1Теория вероятностей и математическая статистика
Основные теоремы исчисления вероятностей
3
Слайд 2Независимые события
Определение
События A и B называются независимыми, если
Слайд 3Пример
Из колоды, насчитывающей 36 карт, наугад извлекается карта. Будут ли
события {извлекли даму} и {извлекли пику} независимы?
Решение.
A = {дама}, B
= {пика}, AB = {дама пик}.
p(A) = 4/36 = 1/9, p(B) = 9/36 = 1/4,
p(AB) = 1/36.
p(A) ∙ p(B) = 1/9 ∙ 1/4 = 1/36.
p(A) ∙ p(B) = p(AB) → A и B независимы.
Слайд 4Замечание
Если события A и B несовместны, то они независимы только
если
P(A) = 0 или P(B) = 0. (ПОЧЕМУ?)
Слайд 5Вероятность события A, вычисленную в предположении, что событие B произошло,
мы будем обозначать через
Условная вероятность
Слайд 6Определение
Условной вероятностью события A при условии, что произошло событие B,
называется число
Считают, что условная
вероятность определена только в случае, когда
P(B) > 0.
Слайд 7Пример
Кубик подбрасывается один раз. Известно, что выпало более трех очков.
Какова при этом вероятность того, что выпало четное число очков?
Решение.
Ω при одном подбрасывании кубика состоит из шести точек: Ω = {1, 2, 3, 4, 5, 6}.
Слова «известно, что выпало более трех очков» означают, что в эксперименте произошло событие B = {4, 5, 6}.
Слайд 8
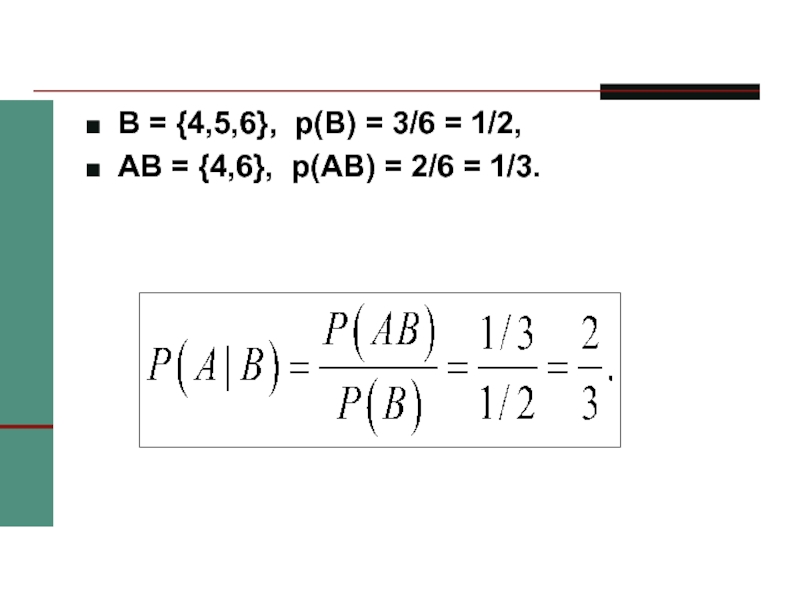
B = {4,5,6}, p(B) = 3/6 = 1/2,
AB = {4,6},
p(AB) = 2/6 = 1/3.
Слайд 9Свойства независимых событий
Если события A и B независимы, то:
P(A|B)
= P(A), P(B|A) = P(B)
(если P(A) >0, P(B) > 0).
независимы
и события
Слайд 10Независимость в совокупности
Определение
События A1, A2, …, An называются независимыми в
совокупности, если для любого набора событий вероятность произведения равна произведению
вероятностей:
Слайд 11Замечание
Если события A1, A2, …, An независимы в совокупности, то
они попарно независимы, т.е. любые два события Ai, Aj независимы.
(ПОЧЕМУ?)
Обратное неверно.
Если события попарно независимы, то
в совокупности могут быть зависимы.
Слайд 14Пример
Из колоды, насчитывающей 36 карт, наугад извлекается карта. Какова вероятность,
что это дама или пика?
Решение.
A = {дама}, B = {пика},
A+B = {дама или пика}, AB = {дама пик}.
p(A) = 4/36, p(B) = 9/36, p(AB) = 1/36.
p(A+B) = p(A) + p(B) – p(AB) =
4/36 + 9/36 – 1/36 = 12/36 = 1/3.
Слайд 16Теорема умножения для двух событий
если соответствующие условные вероятности определены
(то есть если P(A) > 0, P(B) > 0).
Доказательство следует из определения условной вероятности.
Слайд 17Пример
Из букв слова "ВЕРОЯТНОСТЬ" случайно
выбирают 2 буквы. Найти вероятность того,
что выбраны 2 буквы "О".
Решение.
Слайд 18Теорема умножения для n событий
Доказательство проводится по индукции.
Слайд 19Пример
Из букв слова «МАТЕМАТИКА» случайно выбирают 4 буквы и выкладывают
в ряд. Найти вероятность того, что получится слово «ТЕМА».
Слайд 20Гипотезы
Определение
Набор попарно несовместных событий H1, H2, …, Hn таких, что
P(Hi) > 0 для всех i и
называется полной группой
событий.
События, образующие полную группу событий, называются гипотезами.
Слайд 21Теорема (формула полной вероятности)
Пусть A – случайное событие, H1, H2,
…, Hn – полная группа событий (гипотезы),
Тогда вероятность события А может
быть вычислена по формуле:
Слайд 23 Есть 3 завода, производящих одну и ту же продукцию. При
этом 1-й завод производит 25%, 2-й завод – 35% и
3-й завод – 40% всей производимой продукции. Брак составляет 5% от продукции 1-го завода, 3% от продукции 2-го и 4% от продукции
3-го завода. Найти вероятность купить бракованное изделие.
Пример
Слайд 24Решение
Рассмотрим три гипотезы:
Hi = {изделие произведено i-м заводом},
i =
1,2,3.
Вероятности этих событий даны:
P(H1) = 0,25, P(H2) =
0,35, P(H3) = 0,4.
Пусть A = {изделие бракованное}. Причем даны условные вероятности:
P(A|H1) = 0,05, P(A|H2) = 0,03, P(A|H3) = 0,04.
Слайд 25
Полная вероятность равна доле
бракованных изделий в объеме всей
продукции.
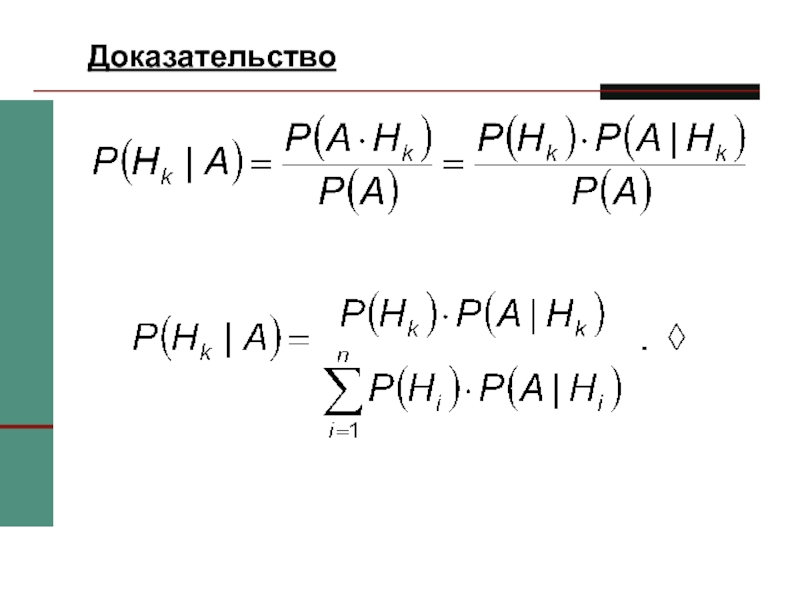
Слайд 26Теорема (Формула Байеса)
Пусть A – случайное событие, H1, H2, …,
Hn – полная группа событий (гипотезы),
Тогда условная вероятность того, что имело
место событие Hk, если наблюдалось событие А, может быть вычислена по формуле:
Слайд 28Пример
По условиям предыдущего примера, найти вероятность, что изделие изготовлено первым
заводом, при условии, что оно бракованное.
Решение
Рассмотрим три гипотезы:
Hi = {изделие
произведено i заводом}, I = 1,2,3.
Вероятности этих событий даны:
P(H1) = 0,25, P(H2) = 0,35, P(H3) = 0,4.
Пусть A = {изделие бракованное}.
Условные вероятности:
P(A|H1) = 0,05, P(A|H2) = 0,03, P(A|H3) = 0,04.
Слайд 29
Тогда вероятность того, что бракованное изделие произведено первым заводом, будет
равна