Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Разбор заданий второй части
Содержание
- 1. Разбор заданий второй части
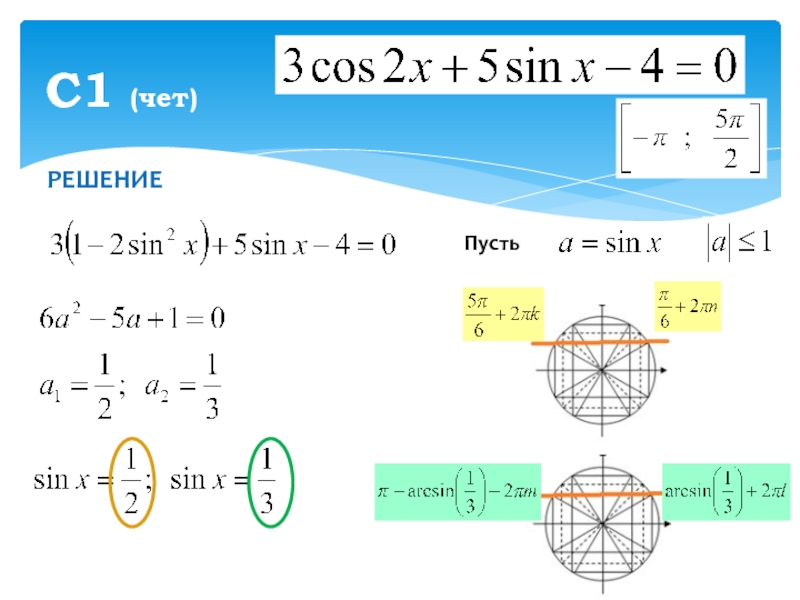
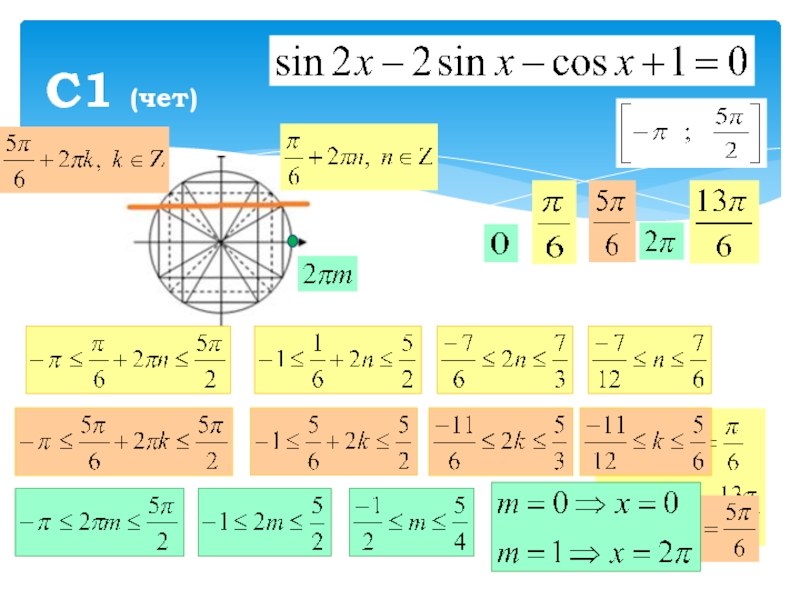
- 2. РЕШЕНИЕС1 (чет)Пусть
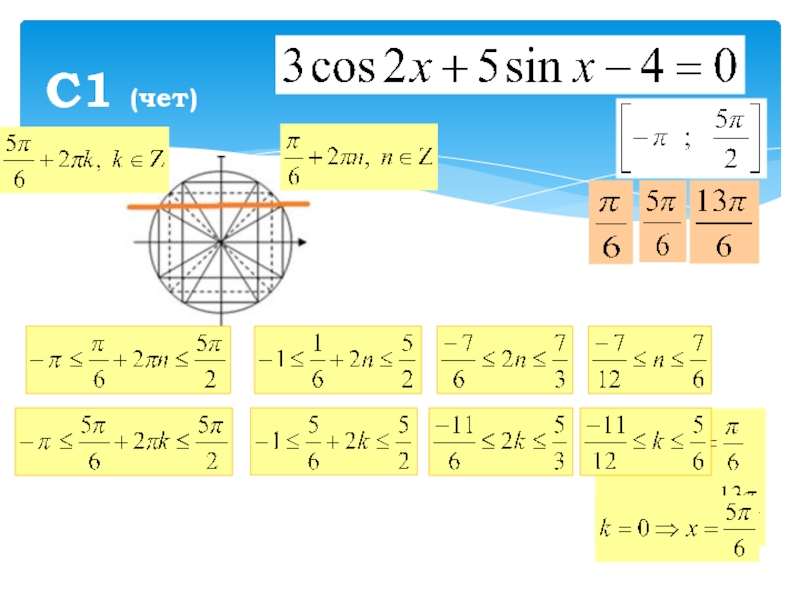
- 3. С1 (чет)
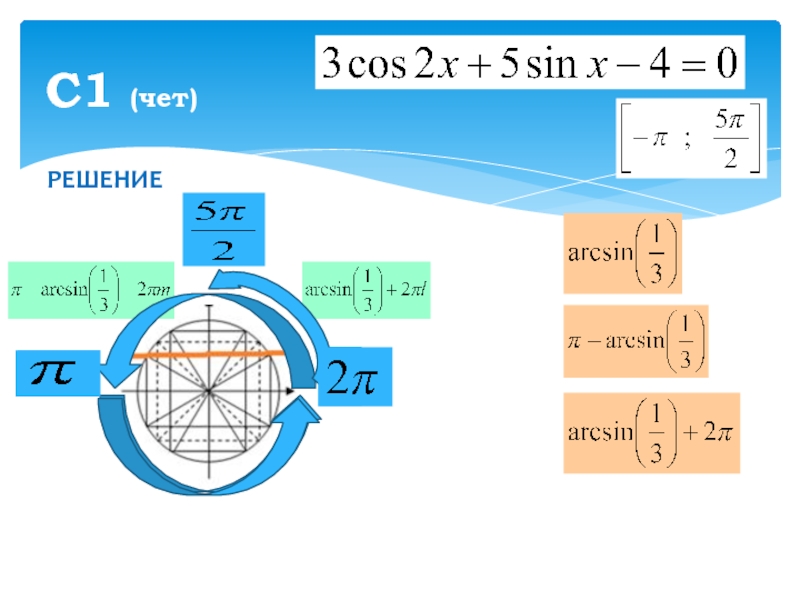
- 4. РЕШЕНИЕС1 (чет)
- 5. ОТВЕТС1 (чет)
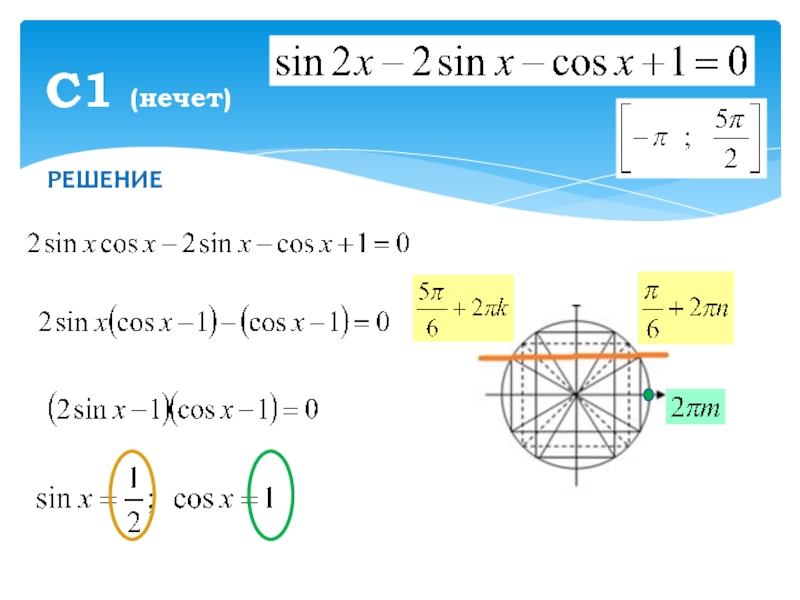
- 6. РЕШЕНИЕС1 (нечет)
- 7. С1 (чет)
- 8. НОРМЫ ОЦЕНОКС11 балл – решение уравнения (бесконечное
- 9. С2В правильной шестиугольной призме ABCDEFB1C1D1E1F1, у которой
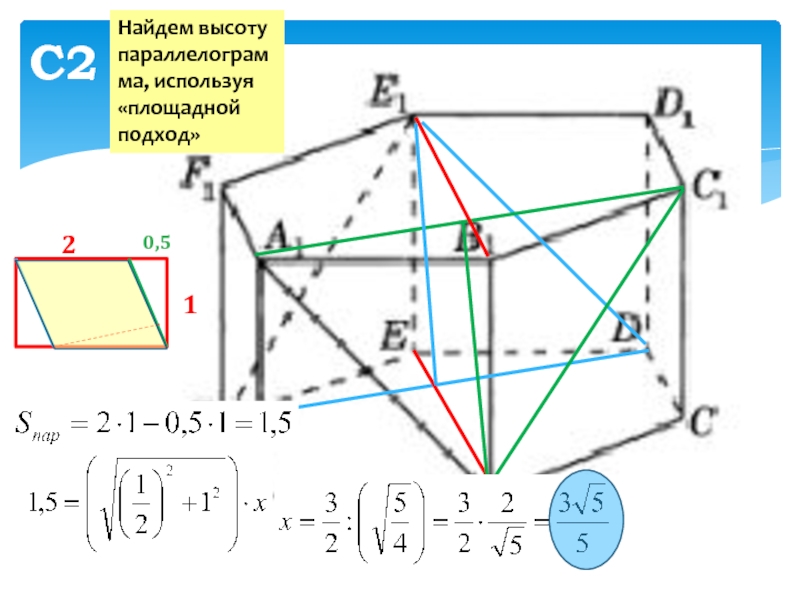
- 10. С2210,5Найдем высоту параллелограмма, используя «площадной подход»
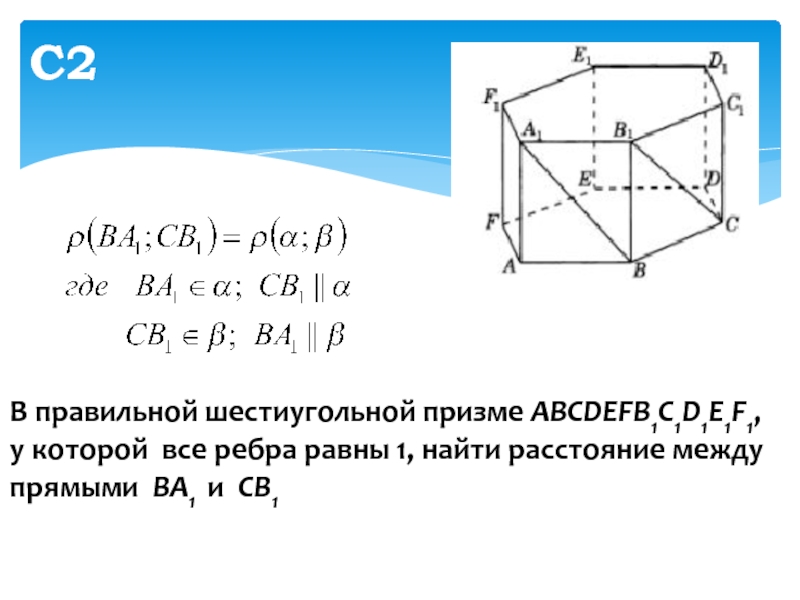
- 11. С2В правильной шестиугольной призме ABCDEFB1C1D1E1F1, у которой
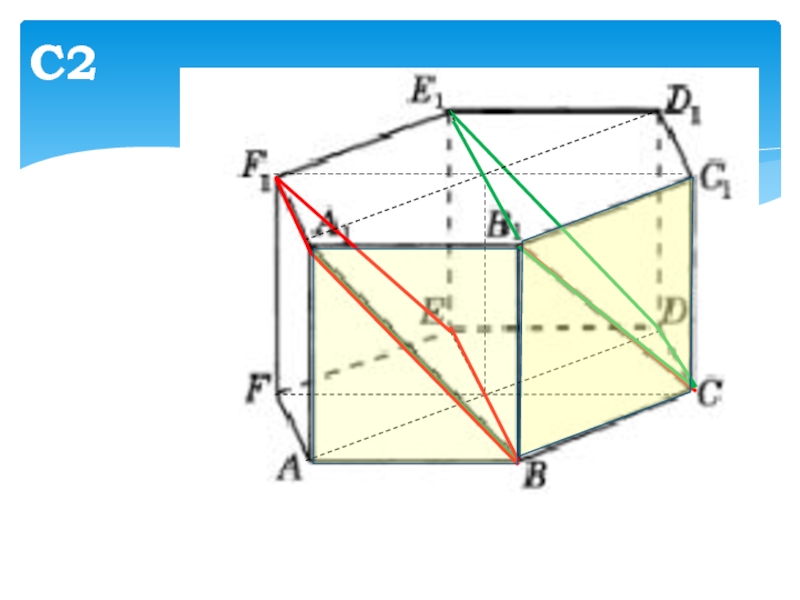
- 12. С2
- 13. С2∨31
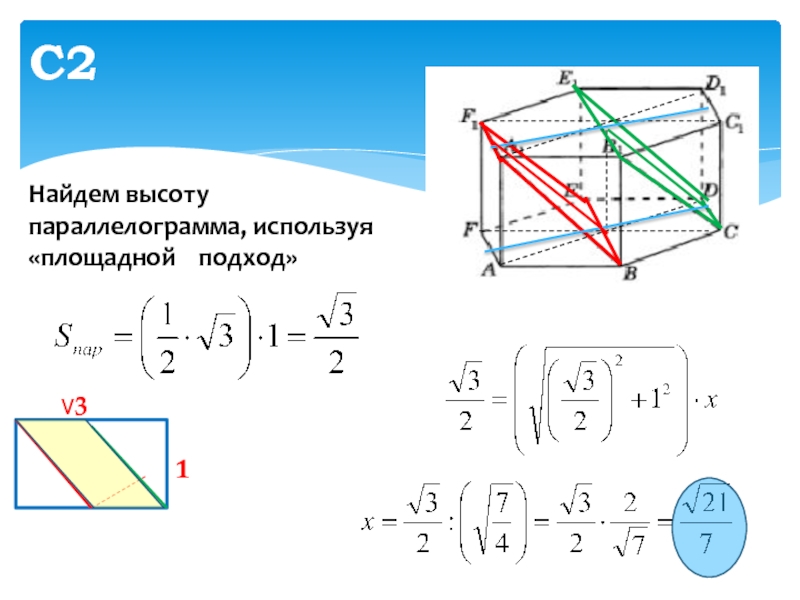
- 14. С2∨31Найдем высоту параллелограмма, используя «площадной подход»
- 15. С2В правильной шестиугольной призме ABCDEFB1C1D1E1F1, у которой
- 16. С2Справочные материалыТипичные задачи МЕТОДА КООРДИНАТхуz1. Уравнение плоскости по трем точкамОбщий вид уравнения плоскостиПри d=1
- 17. С2Справочные материалыТипичные задачи МЕТОДА КООРДИНАТхуz2. Уравнение
- 18. НОРМЫ ОЦЕНОКС21 балл – обоснованный переход к
- 19. РЕШЕНИЕС3 (нечет)0a2-5Однородное неравенство 2 степениРазделим на положительное число(1)При корни вспомогательного квадратного уравнения
- 20. РЕШЕНИЕС3 (нечет)x2-4Сравним значения правой и левой частей неравенстваСравним значения(2)положительно на ОДЗтак как(1)(3)(2)
- 21. РЕШЕНИЕС3 (чет)(1)Оценим каждый множитель в левой части
- 22. РЕШЕНИЕС3 (чет)(2)(1)Сравним значения(3)x3(2)
- 23. НОРМЫ ОЦЕНОКС31 балл – решение одного неравенства+
- 24. Решение.Пусть О – точка пересечения биссектрис.Возможны два
- 25. Решение.МNПусть О – точка пересечения биссектрис.Рассмотрим первый
- 26. В параллелограмме ABCD AB=12, биссектрисы углов при
- 27. С4В параллелограмме ABCD AB=12, биссектрисы углов при
- 28. Удачи на экзамене
- 29. Скачать презентанцию
РЕШЕНИЕС1 (чет)Пусть
Слайды и текст этой презентации
Слайд 8НОРМЫ ОЦЕНОК
С1
1 балл – решение уравнения (бесконечное множество ответов)
+ 1
балл – выделение конкретных ответов из промежутка
(мax 2 балла)
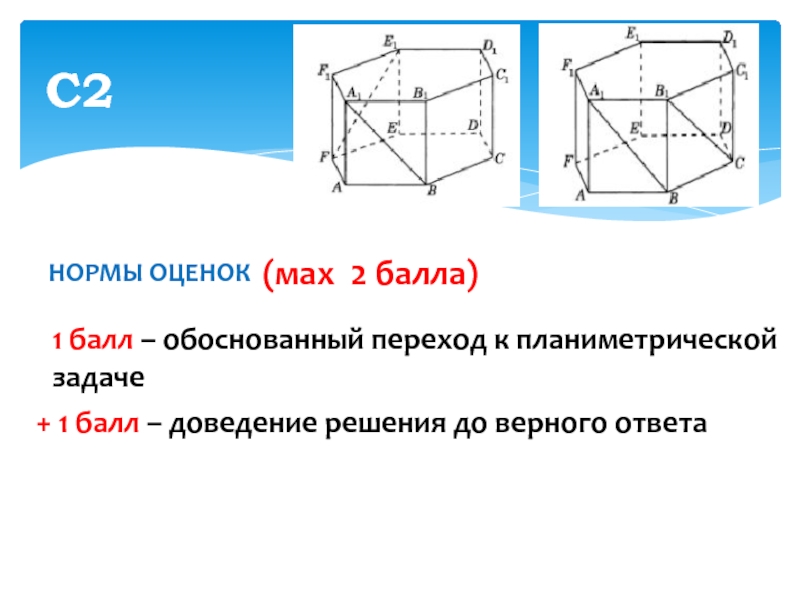
Слайд 9С2
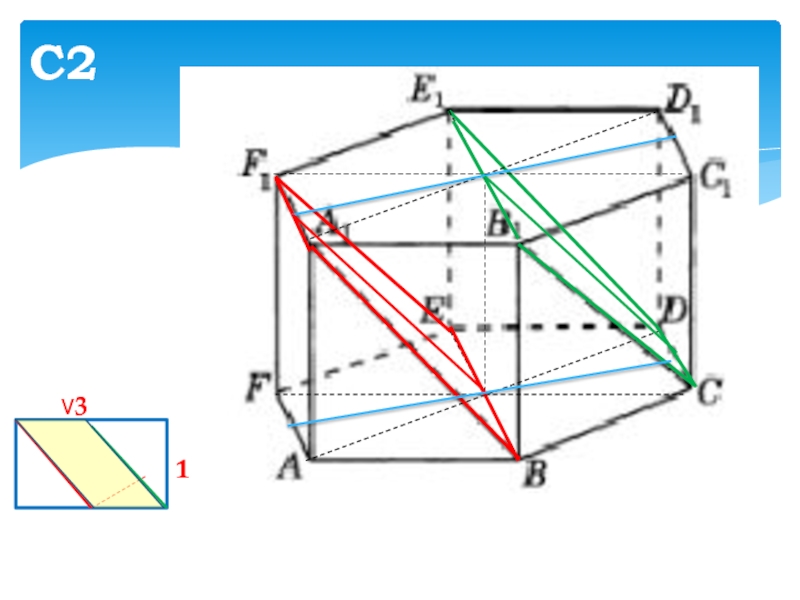
В правильной шестиугольной призме ABCDEFB1C1D1E1F1,
у которой все ребра равны
1, найти расстояние между прямыми ВA1 и FE1
Слайд 11С2
В правильной шестиугольной призме ABCDEFB1C1D1E1F1,
у которой все ребра равны
1, найти расстояние между прямыми ВA1 и CB1
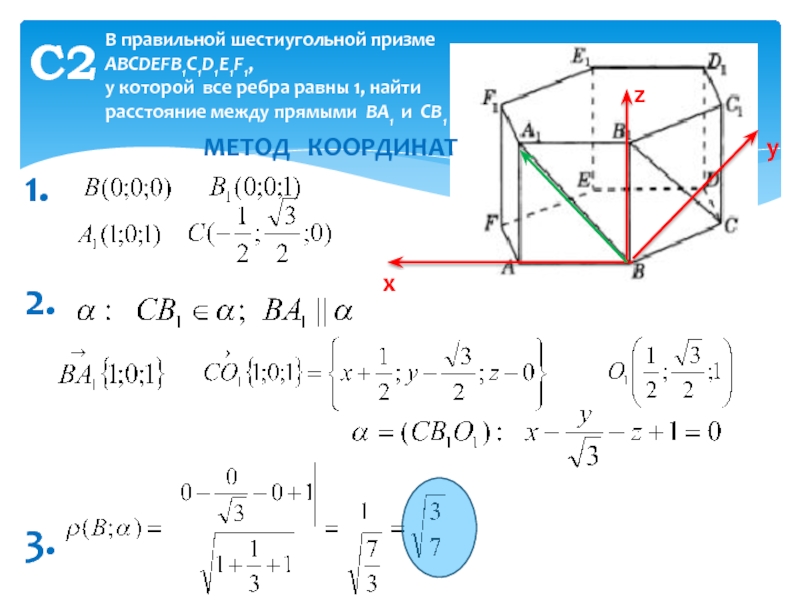
Слайд 15С2
В правильной шестиугольной призме ABCDEFB1C1D1E1F1,
у которой все ребра равны
1, найти расстояние между прямыми ВA1 и CB1
МЕТОД
КООРДИНАТх
у
z
1.
2.
3.
Слайд 16С2
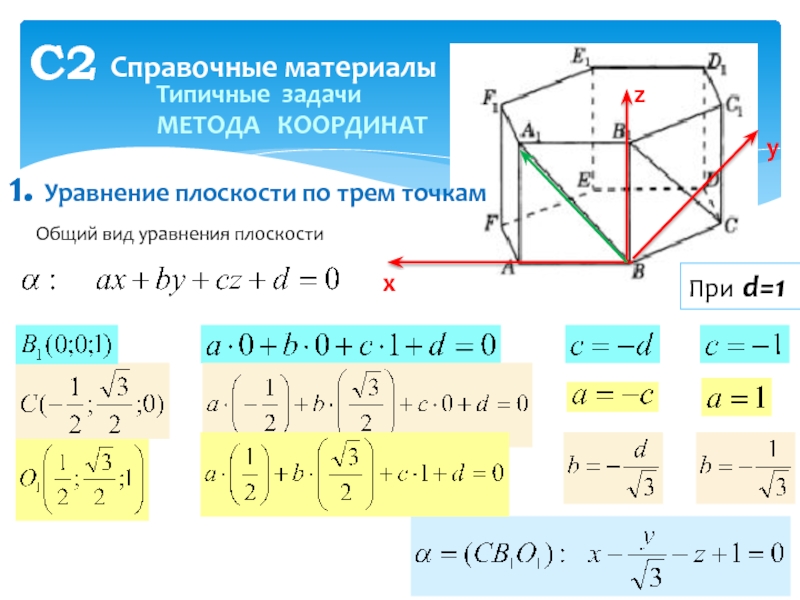
Справочные материалы
Типичные задачи МЕТОДА КООРДИНАТ
х
у
z
1. Уравнение плоскости по трем
точкам
Общий вид уравнения плоскости
При d=1
Слайд 17С2
Справочные материалы
Типичные задачи МЕТОДА КООРДИНАТ
х
у
z
2. Уравнение плоскости
по точке
и вектору нормали
Общий вид уравнения плоскости
При с=-1
где
Найдем d из условия
Слайд 18НОРМЫ ОЦЕНОК
С2
1 балл – обоснованный переход к планиметрической задаче
+
1 балл – доведение решения до верного ответа
(мax 2 балла)
Слайд 19РЕШЕНИЕ
С3 (нечет)
0
a
2
-5
Однородное неравенство 2 степени
Разделим на положительное число
(1)
При
корни вспомогательного квадратного уравнения
Слайд 20РЕШЕНИЕ
С3 (нечет)
x
2
-4
Сравним значения правой и левой частей неравенства
Сравним значения
(2)
положительно на
ОДЗ
так как
(1)
(3)
(2)
Слайд 23НОРМЫ ОЦЕНОК
С3
1 балл – решение одного неравенства
+ 1 балл –
решение второго неравенства
(мax 3 балла)
+ 1 балл – пересечение решений
неравенств
Слайд 24Решение.
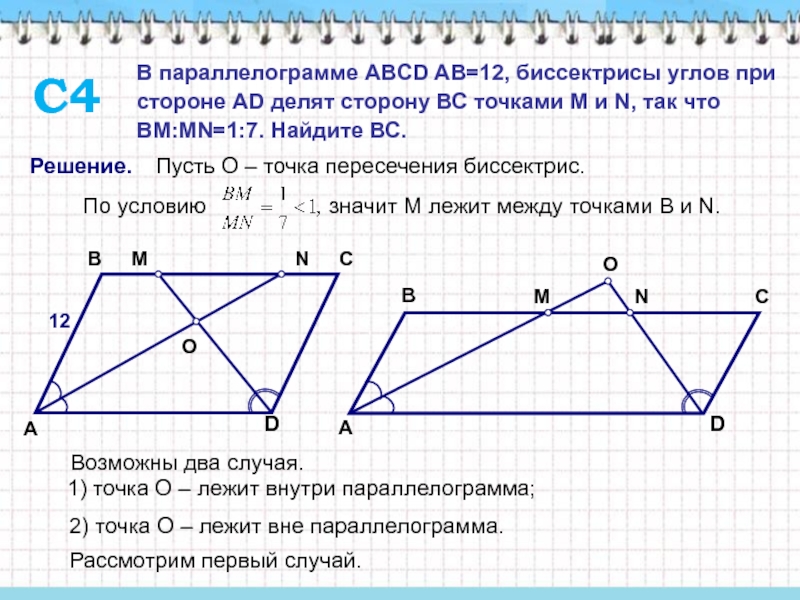
Пусть О – точка пересечения биссектрис.
Возможны два случая.
1) точка О
– лежит внутри параллелограмма;
Рассмотрим первый случай.
2) точка О – лежит
вне параллелограмма.12
В параллелограмме ABCD AB=12, биссектрисы углов при стороне AD делят сторону ВС точками M и N, так что BM:MN=1:7. Найдите ВС.
С4
Слайд 25Решение.
М
N
Пусть О – точка пересечения биссектрис.
Рассмотрим первый случай.
12
1) ABN –
равнобедренный, т.к.
ВNА=NAD- накрест лежащие;
значит ВNА= ВAN и AB=BN=12,
АN – биссектриса
А, тогда
Найдем MN=BN-BM=12-1,5=10,5.
2) Аналогично, DMC – равнобедренный, MC=DC=12.
Тогда NC= MC-MN=12-10,5=1,5.
3) Значит, ВС=ВМ+MN+NC=13,5.
1,5
10,5
1,5
В параллелограмме ABCD AB=12, биссектрисы углов при стороне AD делят сторону ВС точками M и N, так что BM:MN=1:7. Найдите ВС.
С4
Слайд 26В параллелограмме ABCD AB=12, биссектрисы углов при стороне AD делят
сторону ВС точками M и N, так что BM:MN=1:7. Найдите
ВС.Решение.
Рассмотрим второй случай:
точка О – лежит вне параллелограмма.
1)ABМ– равнобедренный, т.к.
Тогда АВ=ВМ=12.
2) Аналогично DNC– равнобедренный,
3) Значит, ВС=ВN+NC=96+12=108.
12
12
12
12
ВMА=MAD- накрест лежащие;
значит ВMА= ВAM.
АМ – биссектриса А,
Ответ: 13,5 или 108.
тогда NC=DC=12.
С4
Слайд 27С4
В параллелограмме ABCD AB=12, биссектрисы углов при стороне AD делят
сторону ВС точками M и N, так что BM:MN=1:7. Найдите
ВС.
