Слайд 1Раздел №4
Солодухин Е.А.
НАЧЕРТАТЕЛЬНАЯ
ГЕОМЕТРИЯ
Слайд 2Базовые преобразования проекций, используемые при решении задач начертательной геометрии
Слайд 3Преобразование прямой общего положения в прямую уровня (построение дополнительной проекции
прямой на плоскости проекций ей параллельной).
Преобразование прямой в проецирующую прямую
(построение дополнительной проекции прямой в виде точки).
Преобразование плоскости общего положения в проецирующую плоскость (построение дополнительной проекции плоскости в виде линии).
Преобразование плоскости общего положения в плоскость уровня (построение дополнительной проекции плоской фигуры на плоскости проекций ей параллельной).
Слайд 4 Практически рассматриваются всего два варианта преобразования.
Вариант 1. Переход
от общего положения объекта в параллельное положение по отношению к
выбранной плоскости проекций - выполняется только на основе прямоугольного варианта метода проецирования.
Вариант 2. Переход от заданного положения объекта в проецирующее положение по отношению к выбранной плоскости проекций - может быть выполнено на основе любого из рассмотренных вариантов метода проецирования.
Слайд 5Базовая задача № 1.
Построение дополнительной проекции прямой линии на параллельной
ей плоскости проекций
(Преобразование прямой общего положения в прямую уровня)
Слайд 6 Задача решается на основе прямоуголь-ного варианта метода проецирования
несколькими способами:
Переменой плоскостей проекций - подбором дополнительной плоскости проекций паралле-льной
заданной прямой.
Плоскопараллельным перемещением – поворо-том прямой до положения параллельного одной из основных плоскостей проекций (предпочтите-льно вращением вокруг проецирующей прямой, как с указанием оси вращения, так и без указа-ния).
Слайд 7Решение задачи способом перемены плоскостей проекций
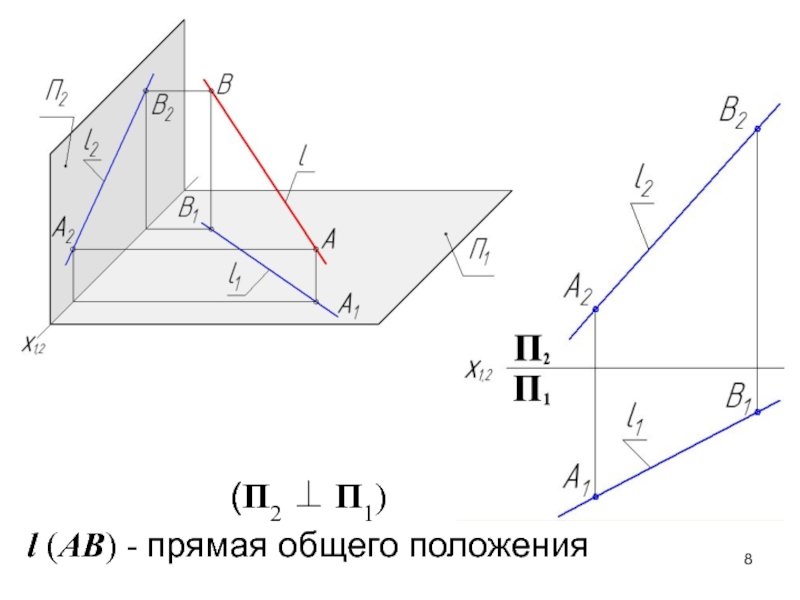
Слайд 8(П2 П1)
l (AB) - прямая общего положения
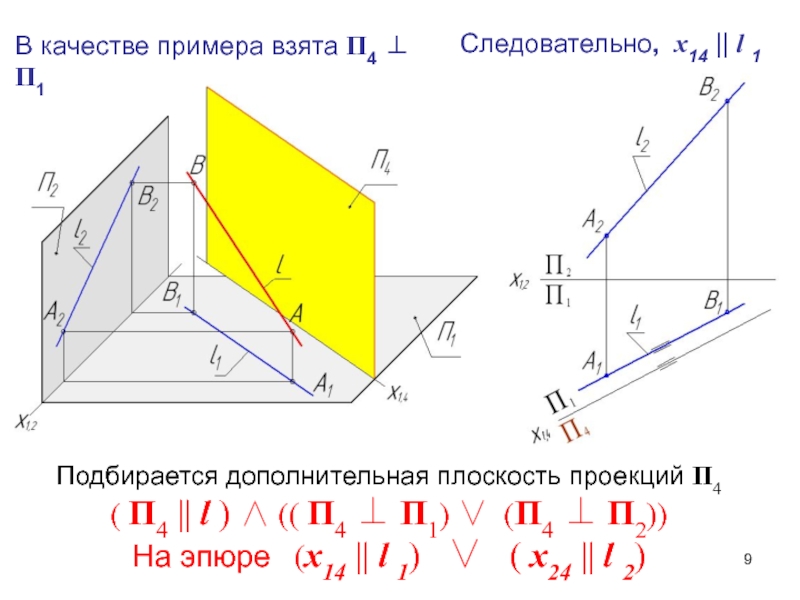
Слайд 9Подбирается дополнительная плоскость проекций П4
( П4 || l )
(( П4 П1) (П4 П2))
На эпюре
(х14 || l 1) ( х24 || l 2)
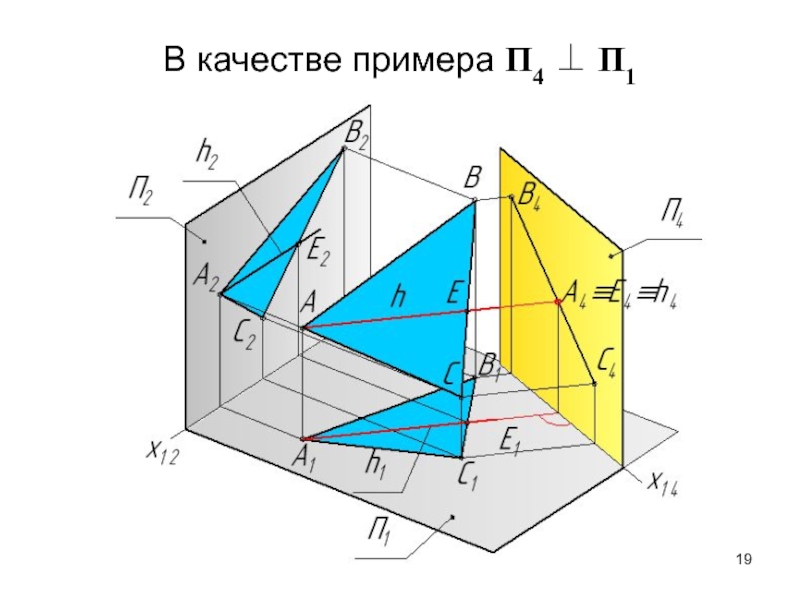
В качестве примера взята П4 П1
Следовательно, х14 || l 1
Слайд 10 Строится дополнительная проекция l (AB) на поле
плоскости П4.
А1А4 х1,4 и В1В4 х1,4 ,
(А2х1,2)
= (А4х1,4) и (В2х1,2) = (В4х1,4)
Слайд 11Построение дополнительной проекции прямой линии в виде точки на основе
дополнительного прямоугольного варианта способа проецирования – перемены (замены) плоскостей проекций
Слайд 12 При прямоугольном проецировании прямая явля-ется проецирующей, если
она перпендикулярна пло-скости проекций.
Следовательно, дополнительная плоскость
проек-ций должна быть перпендикулярна заданной прямой
П′ l ,
Но, если прямая l – прямая общего положения,
то и П′ – плоскость общего положения.
Т.е. П′ П1 и П′ П2
Следовательно, чтобы получить проекцию прямой линии общего положения в виде точки способом перемены плоскостей проекций, нельзя сразу подобрать необходимую плоскость проекций.
Данное преобразование выполняется в два этапа.
Слайд 131-й этап
Прямая преобразуется в прямую уровня
( П4 II l
) (( П4 П1) (П4 П2))
Это рассмотренная ранее
базовая задача №1 на построение проекции прямой общего положения на плоскости проекций ей параллельной.
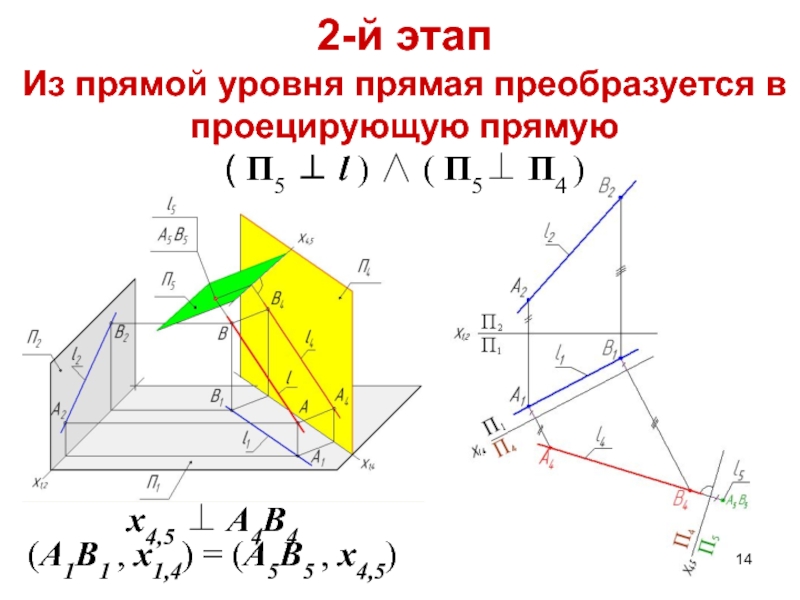
Слайд 142-й этап
Из прямой уровня прямая преобразуется в проецирующую прямую
(
П5 l ) ( П5 П4 )
x4,5
A4B4
(A1B1 , x1,4) = (A5B5 , x4,5)
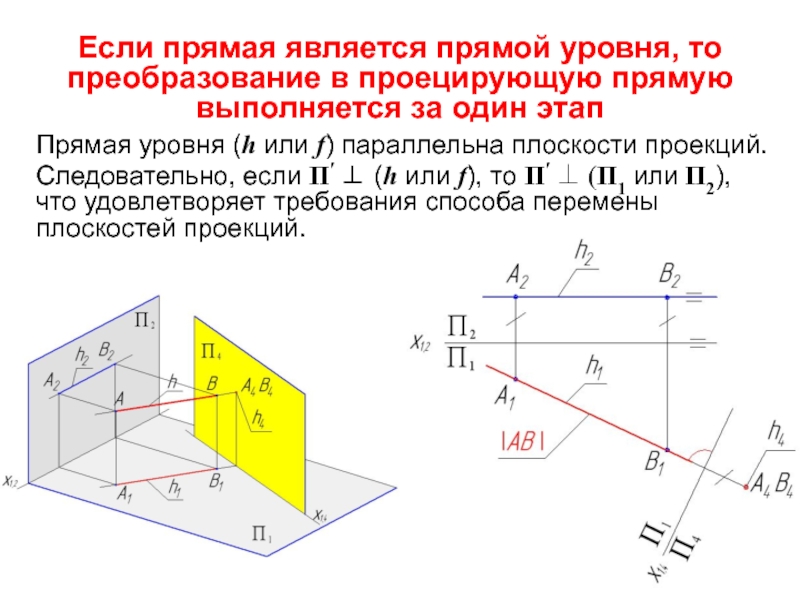
Слайд 15Если прямая является прямой уровня, то преобразование в проецирующую прямую
выполняется за один этап
Прямая уровня (h или f) параллельна плоскости
проекций.
Следовательно, если П′ (h или f), то П′ (П1 или П2), что удовлетворяет требования способа перемены плоскостей проекций.
Слайд 16Базовая задача № 3.
Построение проекции плоскости в виде линии
(Преобразование
плоскости общего положения в проецирующую плоскость)
Слайд 17Построение дополнительной проекции плоскости общего положения в виде прямой линии
способом перемены (замены) плоскостей проекций
Слайд 18 Так как данный способ преобразования основан на прямоугольном
проецировании, то любая плоскость, например Т, является проецирующей, если она
перпен-дикулярна плоскости проекций. Следовательно (П4 Т).
Если (П4 Т), то ((П4 l) ; (l ⊂ Т)).
В то же время дополнительная плоскость проекций П4 должна быть проецирующей по отношению к основным плоскостям проекций П1 или П2 ((П4 П1) (П4 П2))
Следовательно, если (l П4) и ((П4 П1) (П4 П2)),
то (l II П1 l II П2) или (l ≡ h) (l ≡ f )
Следовательно,
если (П4 П1), то (П4 h, h Т) и (x1,4 h1)
если (П4 П2), то (П4 f, f Т) и (x2,4 f2)
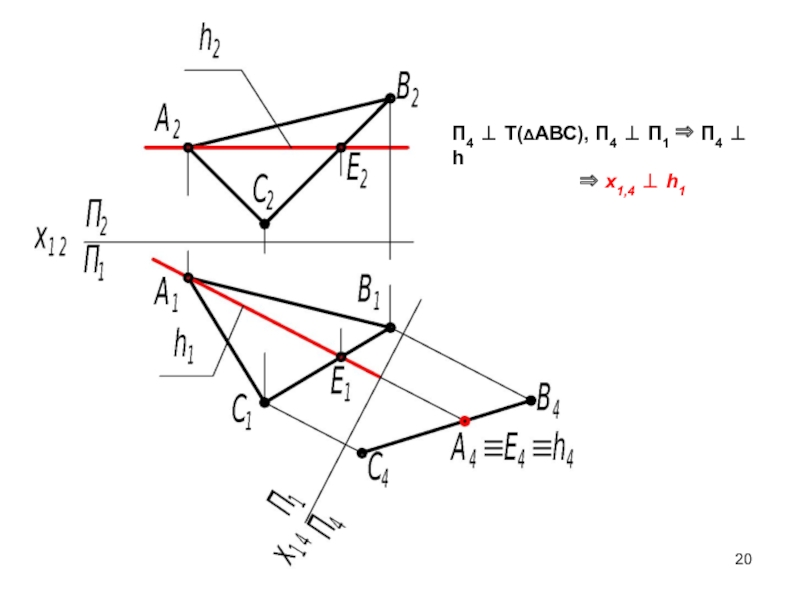
Слайд 20П4 Т(АВС), П4 П1 П4 h
х1,4 h1
Слайд 21Базовая задача № 4.
Построение проекции плоской фигуры на плоскости
проекций ей параллельной
Слайд 22Решение задачи способом перемены (замены) плоскостей проекций
Слайд 23П′ II Т
Так как плоскость Т – плоскость общего положения,
то любая плоскость ей параллельная, в том числе и проекций
П′, также будет плоскостью общего положения, т.е. П′ П1 и П′ П2, что противоречит способу перемены (замены) плоскостей проекций.
Следовательно, задача должна быть решена в два этапа.
1-й этап. П4 Т (базовая задача №3).
2-й этап. П5 II Т.
Слайд 24В качестве примера
1) П4Т(АВС), П4П1П4h
2) П5 II Т(АВС), П5
П4
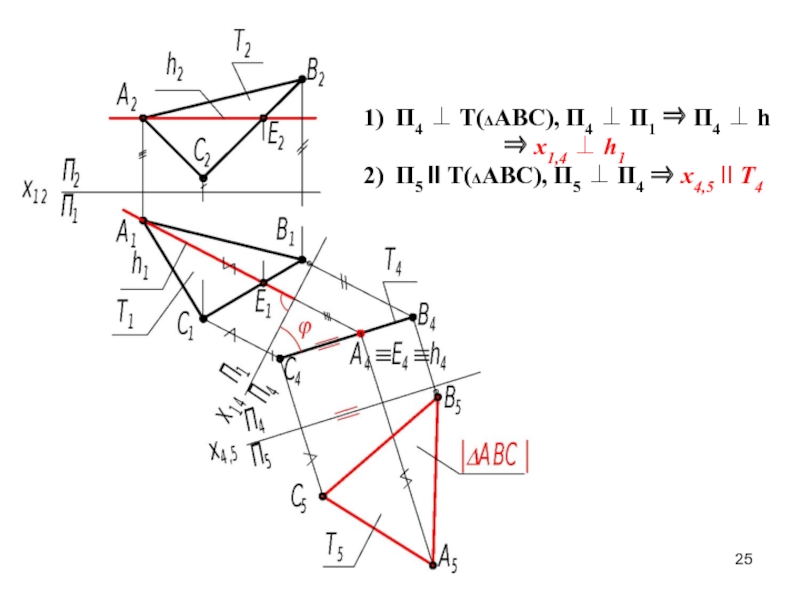
Слайд 251) П4 Т(АВС), П4 П1 П4
h
х1,4 h1
2) П5 II Т(АВС), П5 П4 х4,5 II Т4
Слайд 26Решение задачи способом вращения вокруг прямой уровня
Слайд 27В ходе решения задачи плоская фигура должна быть повернута вокруг
оси, являющейся прямой уровня плоскости, в которой расположена заданная фигура,
до положения параллельного плоскости проекций, параллельно которой расположена ось вращения.
Практически решение задачи сводится к повороту какой-либо одной точки или нескольких точек заданной фигуры (в зависимости от формы фигуры) до указанного положения.
Слайд 28В представленном далее примере в качестве оси вращения взята горизонталь.
Следовательно,
заданная фигура должна быть повернута вокруг выбранной оси до положения
параллельного горизонтальной плоскости проекций.
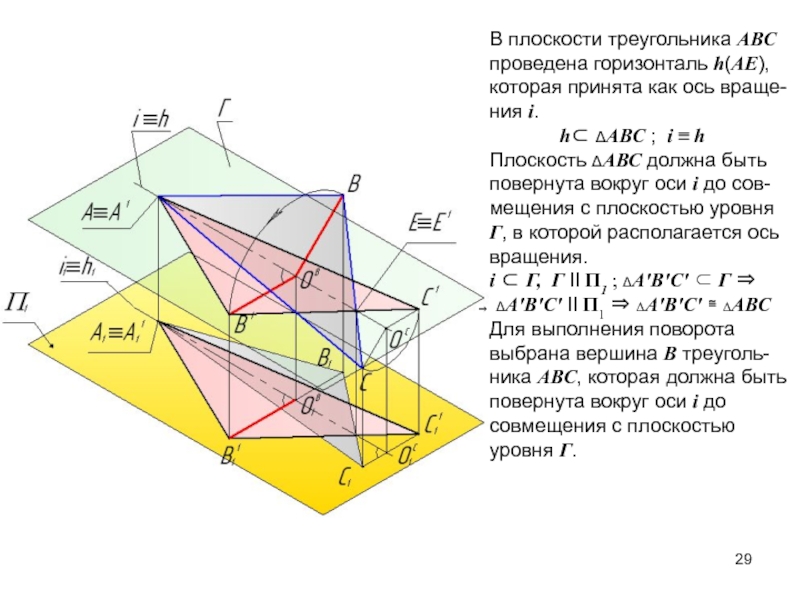
Слайд 29В плоскости треугольника АВС проведена горизонталь h(АЕ), которая принята как
ось враще-
ния i.
h
АВС ; i ≡ h
Плоскость АВС должна быть
повернута вокруг оси i до сов-
мещения с плоскостью уровня Г, в которой располагается ось
вращения.
i Г, Г II П1 ; А′В′С′ Г
А′В′С′ II П1 А′В′С′ АВС
Для выполнения поворота выбрана вершина В треуголь-ника АВС, которая должна быть повернута вокруг оси i до совмещения с плоскостью уровня Г.
Слайд 30Вспомним рассмотренный ранее метод поворота точки вокруг прямой уровня
Слайд 31На рисунке ось вращения i является горизонталью
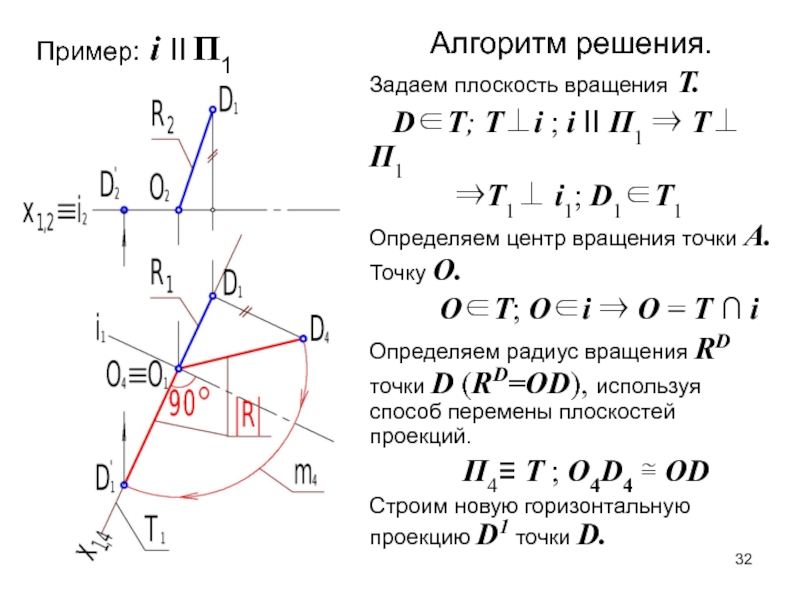
Слайд 32 Алгоритм решения.
Задаем плоскость вращения T.
DТ; Тi ; i II П1 Т П1
Т1 i1; D1Т1
Определяем центр вращения точки А. Точку О.
ОТ; Оi О = Т ∩ i
Определяем радиус вращения RD точки D (RD=ОD), используя способ перемены плоскостей проекций.
П4≡ Т ; О4D4 ОD
Строим новую горизонтальную проекцию D1 точки D.
Пример: i II П1
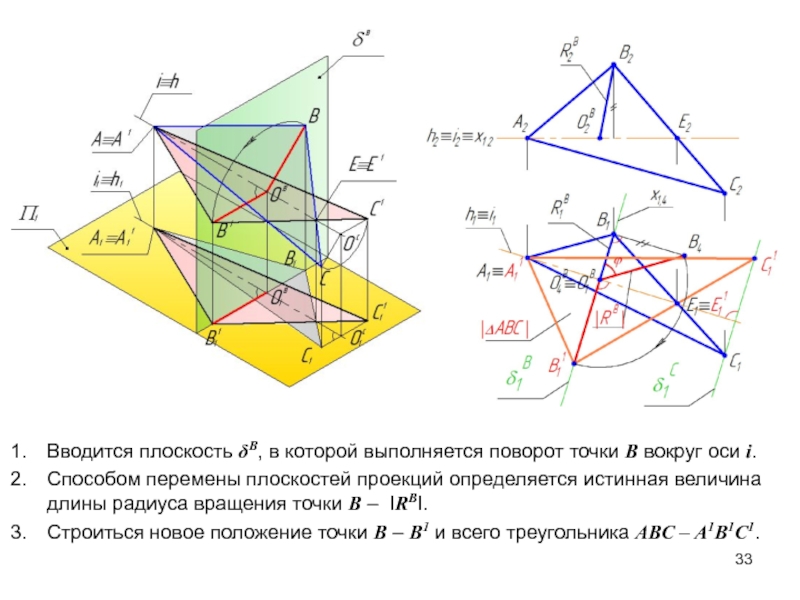
Слайд 33Вводится плоскость δВ, в которой выполняется поворот точки В вокруг
оси i.
Способом перемены плоскостей проекций определяется истинная величина длины
радиуса вращения точки В – IRBI.
Cтроиться новое положение точки В – В1 и всего треугольника АВС – А1В1С1.
Слайд 34Решение задачи способом совмещения плоскости общего положения с какой-либо плоскостью
проекций
(вращение вокруг следа плоскости)
Слайд 35Вспомним рассмотренный ранее метод совмещения плоскости общего положения с плоскостью
проекций путем ее поворота вокруг следа этой плоскости
Слайд 36Пример.
Совместить плоскость Р(h0, f0 ) с горизонтальной плоскостью проекций П1
поворотом вокруг горизонтали h0.
Задаем на плоскости Р точку, например, точку
1. 1f0.
Отмечаем ось вращения i. i h0.
Задаем плоскость Т – плоскость вращения точки 1.
1Т; Т (i h0); (i h0) П1 Т П1 Т1 (i1 h01); 11Т1
Так как 1Т, то и после перемещения точка 1 остается в плоскости Т, т.е. 11Т и 111Т1.
Определяем положение точки 111.
Так Рх12=Рх1 - истинная величина отрезка, то с помощью циркуля переносим точку 1 на горизонтальную проекцию плоскости Т.
Через точки Рх и 111 проводим прямую и обозначаем f011 – новая проекция фронтали f0
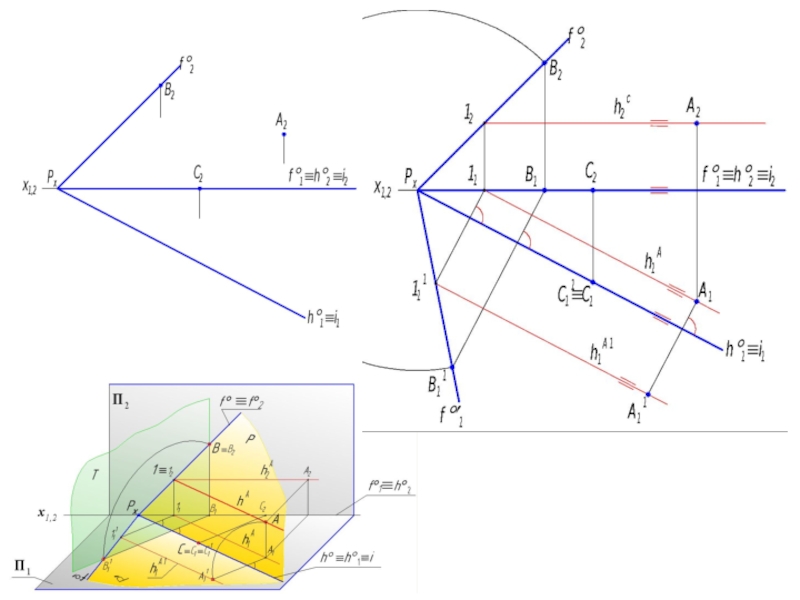
Слайд 37Задана плоскость Р (h°, f°).
Заданы три точки А, В, С,
принадлежащие плоскости Р ({А,В,С} P).
А – общее положение; В
f°; С h°.
Строятся горизонтальная и фронтальная проекции точек А, В, С.
АР А hA, hA Р.
Выполняется совмещение плоскости Р с плоскостью проекций П1. (i h°).
В f° В1 f°1, С(i h°) С1 С, А hA А1 hA1
Слайд 40Метрическими называются задачи, в ходе решения которых определяется значение измеряемой
величины – расстояния между двумя точками (длина отрезка), величины линейного
угла или истинной формы и размеров плоской фигуры.
При решении метрических задач применя-ется только прямоугольный вариант метода проецирования.