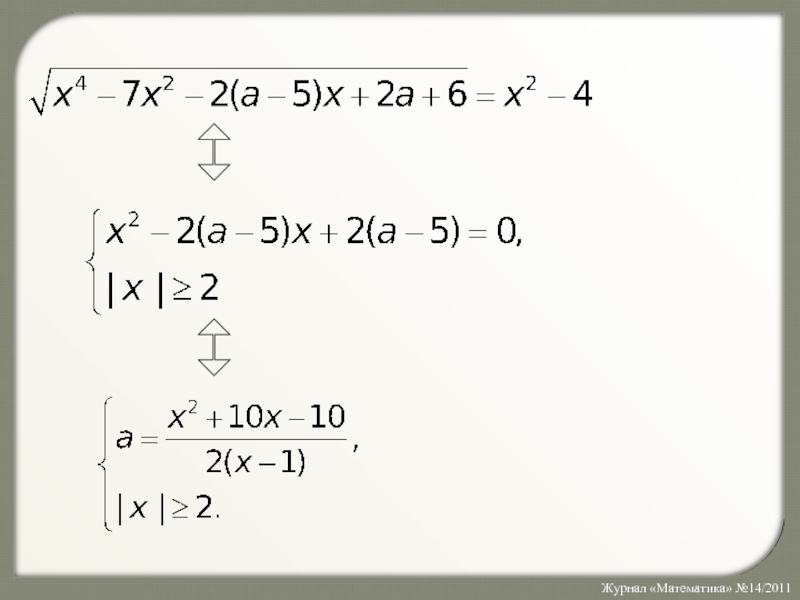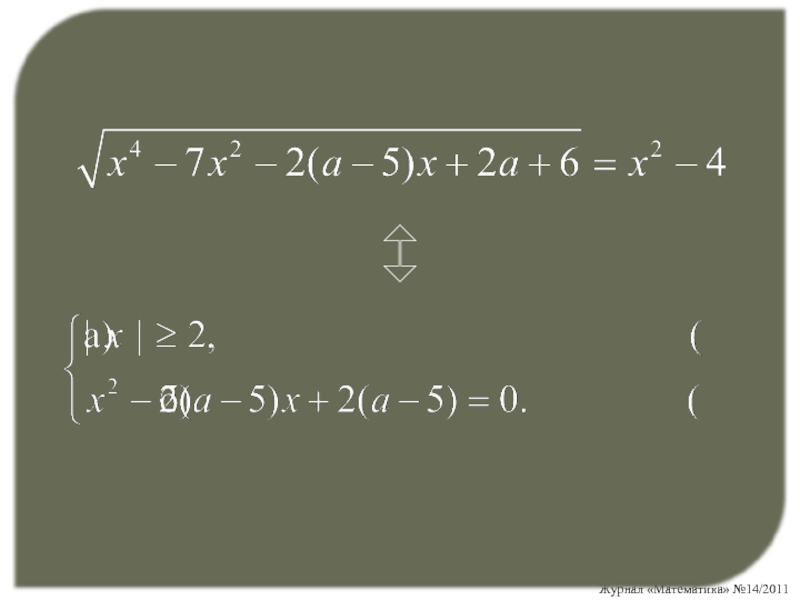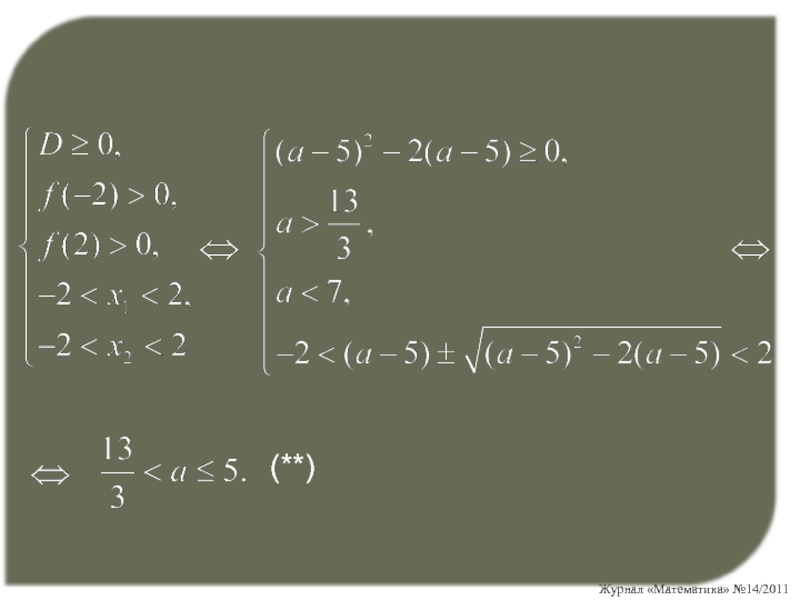Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Различные способы решения задач с параметрами
Содержание
- 1. Различные способы решения задач с параметрами
- 2. Задача 1 Найдите все значения параметра а, при которых уравнение имеет хотя бы один корень.
- 3. Слайд 3
- 4. График левой части уравнения y = a —
- 5. 3. Найдем производную:
- 6. 4. Найдем критические точки функции: ymax = y(0)
- 7. 6. Найдем значения функции в точках ±2: f(2)
- 8. Ответ: и .
- 9. Задача 2 Найдите значения параметра а, при которых уравнение не имеет решения.
- 10. Слайд 10
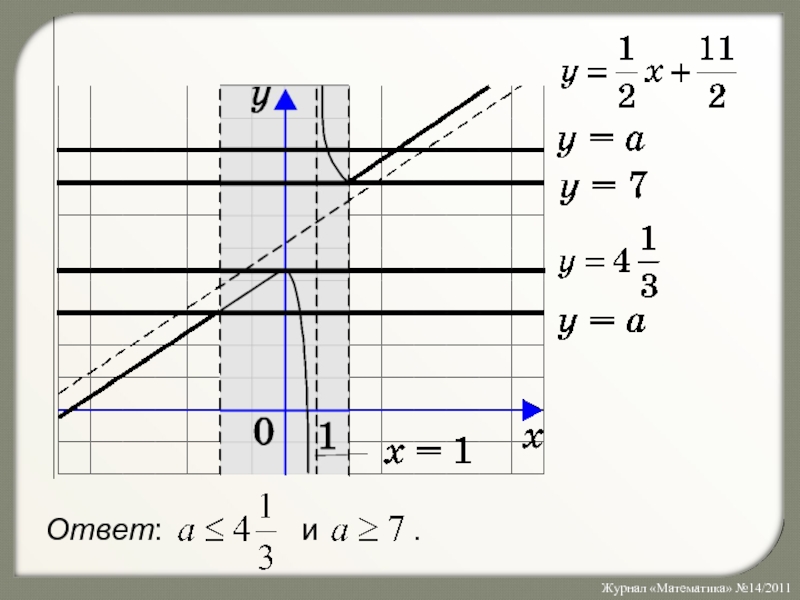
- 11. Условие (а) не выполняется при x
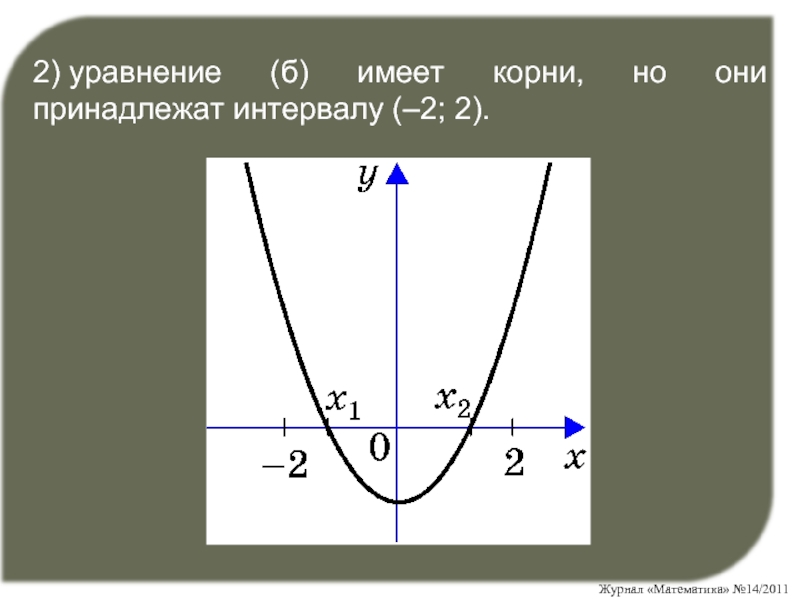
- 12. 2) уравнение (б) имеет корни, но они принадлежат интервалу (–2; 2).
- 13. (**)
- 14. Объединяя множества (*) и (**), получаем: Итак,
- 15. Указания.Возможные способы решения:— используя теорему равносильности;— используя замену переменной;— графический
- 16. Слайд 16
- 17. Чтобы исходное уравнение имело ровно один корень,
- 18.
- 19. Рассмотрим случай, когда квадратное уравнение имеет два
- 20. Рассмотрим неравенство при всех a <
- 21. Исходное уравнение имеет один корень при тех
- 22. Если D = 0, a = 1,25,
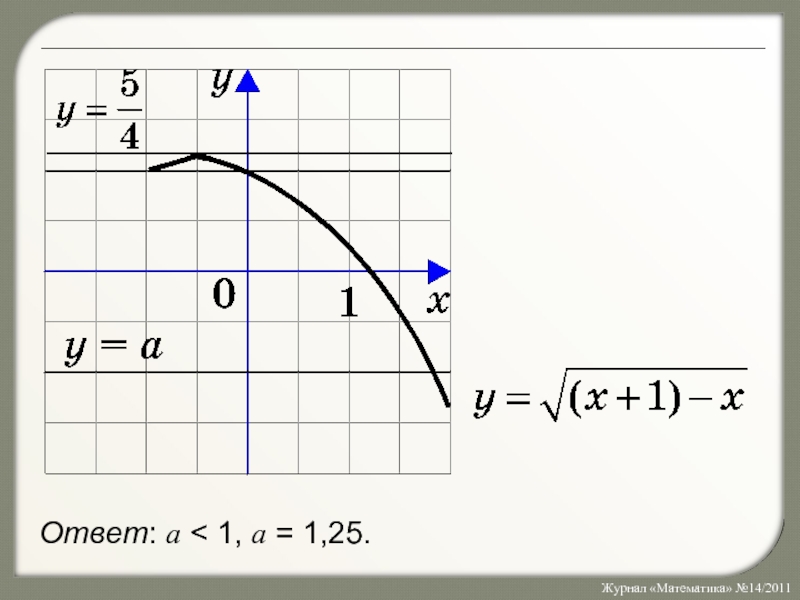
- 23. Преобразуем уравнение к виду Построим график функции, стоящей в левой части уравнения:
- 24. Алгоритм.1. Найдем область определения функции.2. Найдем точки
- 25. Ответ: a < 1, a = 1,25.
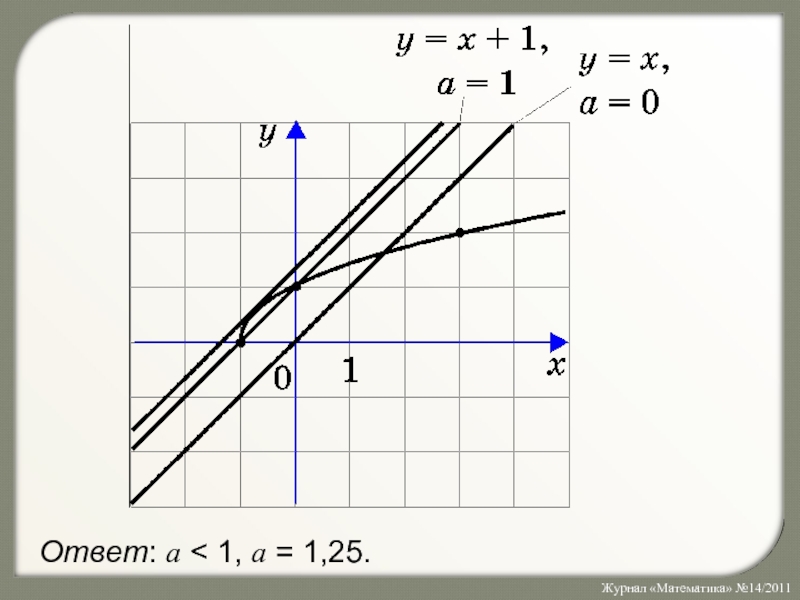
- 26. Построим график левой и правой частей уравнения: y = x + a.
- 27. Ответ: a < 1, a = 1,25.
- 28. Скачать презентанцию
Слайды и текст этой презентации
Слайд 4
График левой части уравнения y = a — прямая, параллельная оси
Ox. Построим график правой части уравнения:
Слайд 6
4. Найдем критические точки функции:
ymax = y(0) = 5, ymin
= y(2) = 7.
5. Найдем асимптоты:
x = 1 — вертикальная асимптота;
— наклонная асимптота
( ).
Слайд 7
6. Найдем значения функции в точках ±2:
f(2) = 7,
Отметим
ограничение, данное в системе: полосу от –2 до 2, включая
границы.
Слайд 11Условие (а) не выполняется при x (–2; 2).
Условие
(б) не выполняется в двух случаях:
1) уравнение (б) не имеет корней,
то есть D < 0:(a – 5)2 – 2(a – 5) < 0 a (5; 7); (*)
Слайд 14Объединяя множества (*) и (**), получаем:
Итак, если
, то уравнение не имеет
решений, значит, при всех других
значениях параметра a решения есть.Ответ: и .
Слайд 15Указания.
Возможные способы решения:
— используя теорему равносильности;
— используя замену переменной;
— графический способ;
— ваши варианты.
Задача 3
Найдите значения параметра а, при каждом из которых уравнение
имеет только одно решение. Слайд 17
Чтобы исходное уравнение имело ровно один корень, надо потребовать, чтобы
получившееся квадратное уравнение имело:
один корень, для которого выполнено условие
Слайд 19Рассмотрим случай, когда квадратное уравнение имеет два корня, то есть
D > 0:
5 – 4a > 0 ⇔ a
< 1,25;
x– < – a ≤ x+,
Слайд 21
Исходное уравнение имеет один корень при тех и только тех
значениях а, при которых полученное уравнение имеет один неотрицательный корень.
Пусть t ≥ 0, x = t2 – 1.
Получим уравнение t2 – t – 1 + а = 0. (*)
Слайд 22Если D = 0, a = 1,25, то есть t
= 0,5 > 0. Значит, исходное уравнение при а =
1,25 имеет один корень.Если D > 0, то есть a < 1,25, уравнение (*) имеет два корня. При этом если a – 1 < 0, то эти корни разных знаков, то есть только один из них положительный.
При а < 1 уравнение (*) имеет один положительный корень, значит и исходное уравнение имеет один корень.
Ответ: a < 1, a = 1,25.