Слайд 14.1 Силы Ван-дер-Ваальса
ЛЕКЦИЯ 4. РЕАЛЬНЫЕ ГАЗЫ
Слайд 2Взаимодействие молекул
При анализе свойств реальных газов необходимо учитывать взаимодействие между
молекулами газа, а также конечное значение объема молекул газа.
Способность твердых
тел сопротивляться растяжению, особые свойства поверхности жидкости и другие явления приводят к выводу, что между молекулами действуют силы притяжения.
Малая сжимаемость весьма плотных газов и особенно жидких и твердых тел означает, что между молекулами существуют силы отталкивания.
Заметим, что в твердых и жидких телах силы притяжения и отталкивания действуют одновременно; если бы это было не так, то тела не были бы устойчивыми.
Слайд 3Зависимость сил межмолекулярного взаимодействия от расстояния между молекулами
В ряде случаев
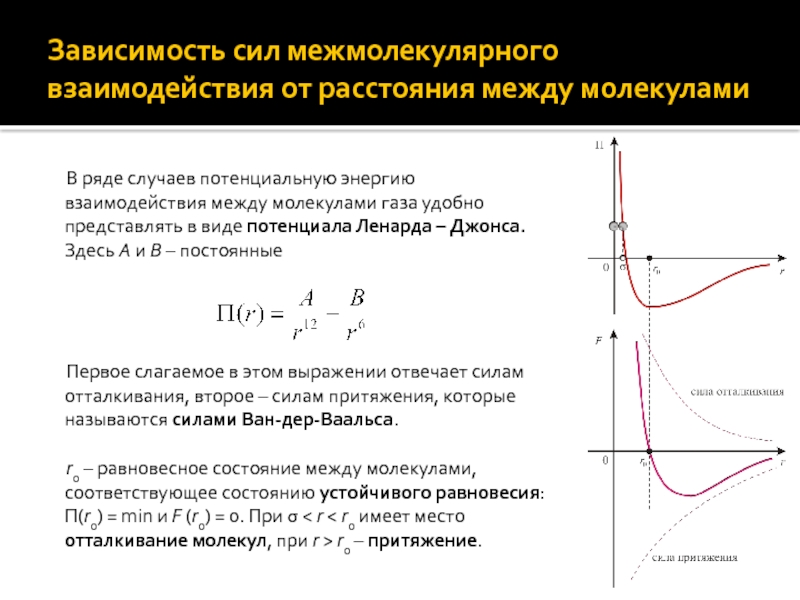
потенциальную энергию взаимодействия между молекулами газа удобно представлять в виде
потенциала Ленарда – Джонса. Здесь A и B – постоянные
Первое слагаемое в этом выражении отвечает силам отталкивания, второе – силам притяжения, которые называются силами Ван-дер-Ваальса.
r0 – равновесное состояние между молекулами, соответствующее состоянию устойчивого равновесия: Π(r0) = min и F (r0) = 0. При σ < r < r0 имеет место отталкивание молекул, при r > r0 – притяжение.
Слайд 4Физическая природа сил Ван-дер-Ваальса
На больших расстояниях от атома его электрическое
поле в целом почто равно нулю и атомы вещества слабо
взаимодействуют друг с другом.
Слайд 5Физическая природа сил Ван-дер-Ваальса
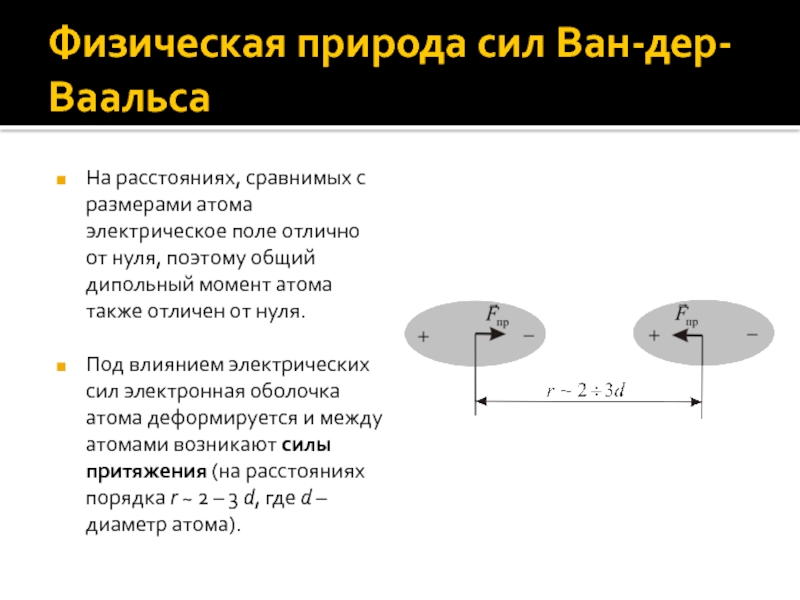
На расстояниях, сравнимых с размерами атома электрическое
поле отлично от нуля, поэтому общий дипольный момент атома также
отличен от нуля.
Под влиянием электрических сил электронная оболочка атома деформируется и между атомами возникают силы притяжения (на расстояниях порядка r ~ 2 – 3 d, где d – диаметр атома).
Слайд 6Физическая природа сил Ван-дер-Ваальса
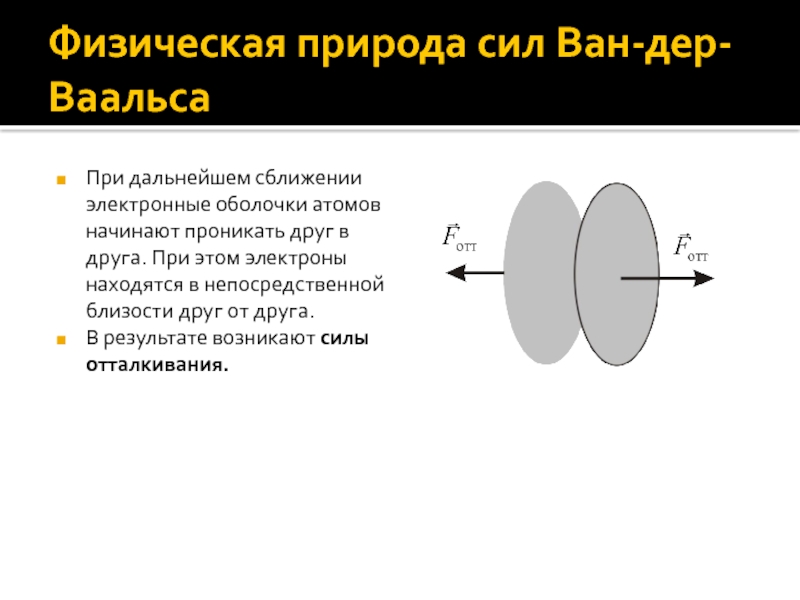
При дальнейшем сближении электронные оболочки атомов начинают
проникать друг в друга. При этом электроны находятся в непосредственной
близости друг от друга.
В результате возникают силы отталкивания.
Слайд 74.2 Уравнение
Ван-дер-Ваальса
ЛЕКЦИЯ 4. РЕАЛЬНЫЕ ГАЗЫ
Слайд 8Уравнение Ван-дер-Ваальса
Уравнение, описывающее поведение газов в широком интервале давлений и
плотностей, было получено Ван-дер-Ваальсом путем внесения поправок в уравнение состояния
идеального газа:
Здесь a и b – постоянные Ван-дер-Ваальса, которые для различных газов имеют различные значения и определяется экспериментально. Таким образом, уравнение Ван-дер-Ваальса не является универсальным.
Слайд 9Физический смысл поправки b Ван-дер-Валльса
Любое вещество состоит из молекул, которые
сами занимают некоторый объем. Следовательно, при движении молекул им предоставлен
не весь объем V сосуда, а меньший на величину объема всех молекул газа (V - b), т.е., в первом приближении, b характеризует суммарный объем всех молекул газа.
Размерность поправки b: [b] = м3/моль
На самом деле (!) для движения молекул запрещен объем 4πd3/3, где d – эффективный диаметр молекулы; в расчете на один атом этот объем будет вдвое меньше: 2πd3/3. Объем самого атома πd3/6, т.е. в 4 раза меньше запрещенного объема. Следовательно, константа b численно равна учетверенному объему всех молекул газа.
Слайд 10Физический смысл поправки a Ван-дер-Валльса
Предположим, что взаимодействие между молекулами вдруг
прекратилось, тогда для их удержания в некотором объеме понадобилось бы
дополнительное внешнее давление.
Следовательно, давление, оказываемое реальным газом на стенки сосуда, меньше давления, производимого идеальным газом, на величину, называемую внутренним давлением. Найдем его.
Слайд 11Физический смысл поправки a Ван-дер-Валльса
Мысленно представим молекулы в виде двух
групп 1 и 2.
Сила, действующая на одну молекулу группы 1
со стороны молекул группы 2 пропорциональна концентрации этих молекул: F1 ~ n. Сила, действующая на все молекулы группы 1 со стороны всех молекул группы 2, пропорциональна силе F1 и их концентрации, т.е. F ~ n2.
Поскольку внутреннее давление зависит от сил взаимодействия между молекулами, то, очевидно, pвнутр~ n2 ~1/V2.
Размерность поправки a: [a] = Па⋅м6/моль2
Слайд 124.3 Изотермы
Ван-дер-Ваальса
ЛЕКЦИЯ 4. РЕАЛЬНЫЕ ГАЗЫ
Слайд 13Изотермы Ван-дер-Ваальса
Уравнение Ван-дер-Ваальса для одного моля газа имеет вид
После раскрытия
скобок это уравнение можно привести к следующему виду
При постоянной температуре
(T = const) это уравнение описывает изотермы Ван-дер-Ваальса. Оно является уравнением 3-й степени относительно V и может иметь либо один вещественный, либо три вещественных корня.
Слайд 14Изотермы Ван-дер-Ваальса
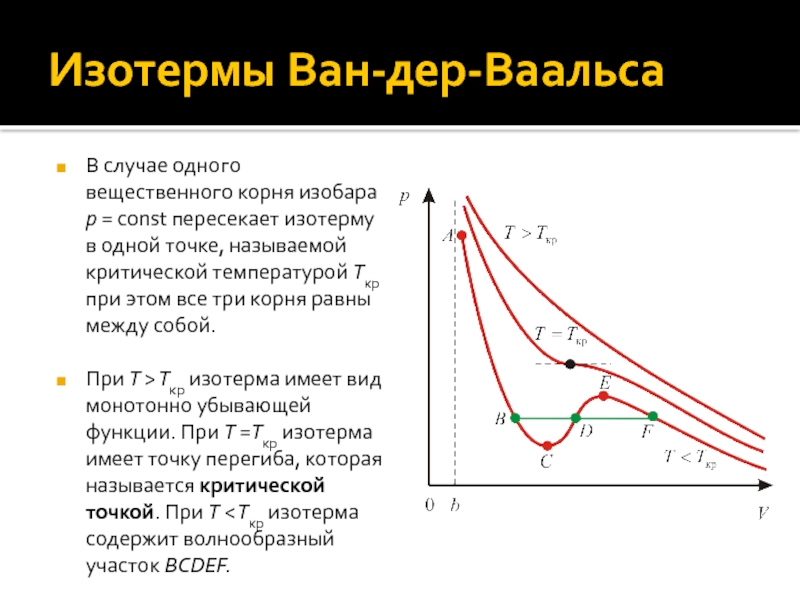
В случае одного вещественного корня изобара p = const
пересекает изотерму в одной точке, называемой критической температурой Tкр при
этом все три корня равны между собой.
При T > Tкр изотерма имеет вид монотонно убывающей функции. При T =Tкр изотерма имеет точку перегиба, которая называется критической точкой. При T < Tкр изотерма содержит волнообразный участок BCDEF.
Слайд 15Критические параметры
Критической температуре Tкр соответствуют критические давление pкр и критический
объем Vкр. Значения критических параметров можно найти из системы уравнений
– уравнения Ван-дер-Ваальса, а также уравнений, отражающих условия того, что в критической точке
Критические параметры равны
Слайд 16Приведенное уравнение
Ван-дер-Ваальса
Введем приведенные температуру, давление и объем, взяв в
качестве единиц измерения критические значения этих величин:
В этом случае уравнение
Ван-дер-Ваальса принимает вид
Такое приведенное уравнение состояния не содержит никаких индивидуальных констант вещества, поэтому оно одинаково для всех веществ
Слайд 17Условие термодинамической устойчивости
Для того, чтобы состояние вещества, описываемое уравнение Ван-дер-Ваальса,
могло реализоваться в действительности, необходимо, чтобы оно было термодинамически устойчивым.
Для этого должно выполняться условие
которое означает, что при увеличении давления объем вещества должен уменьшаться.
Слайд 18Условие ТД-устойчивости и изотермы Ван-дер-Ваальса
Из этого условия следует, что давление
p на изотермах Ван-дер-Ваальса при возрастании объема должно монотонно убывать.
Условие термодинамической устойчивости выполняется для всех изотерм при T > Tкр, однако при T < Tкр изотермы Ван-дер-Ваальса имеют возрастающий участок CDE, для которого это условие является нарушенным. Это означает, что состояния, отвечающие точкам этого участка, не могут реализоваться на практике.
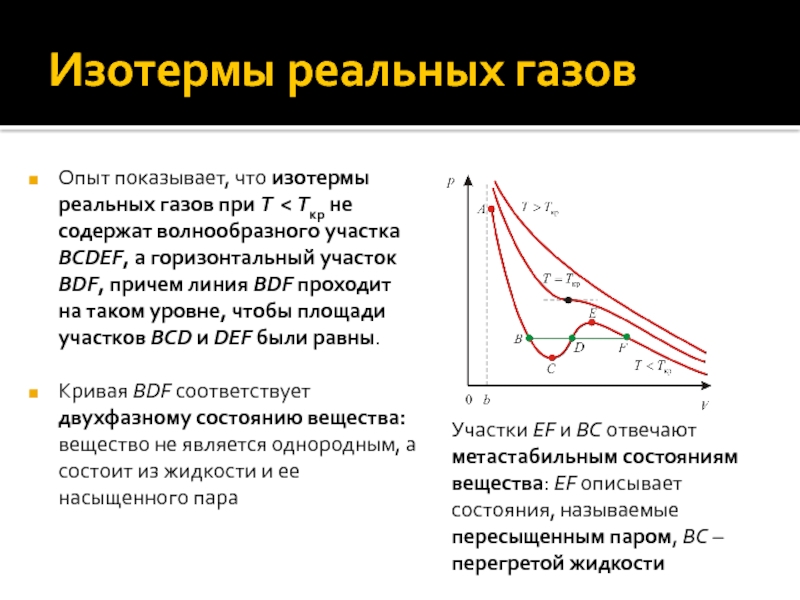
Слайд 19Изотермы реальных газов
Опыт показывает, что изотермы реальных газов при T
< Tкр не содержат волнообразного участка BCDEF, а горизонтальный участок
BDF, причем линия BDF проходит на таком уровне, чтобы площади участков BCD и DEF были равны.
Кривая BDF соответствует двухфазному состоянию вещества: вещество не является однородным, а состоит из жидкости и ее насыщенного пара
Участки EF и BC отвечают метастабильным состояниям вещества: EF описывает состояния, называемые пересыщенным паром, BC – перегретой жидкости
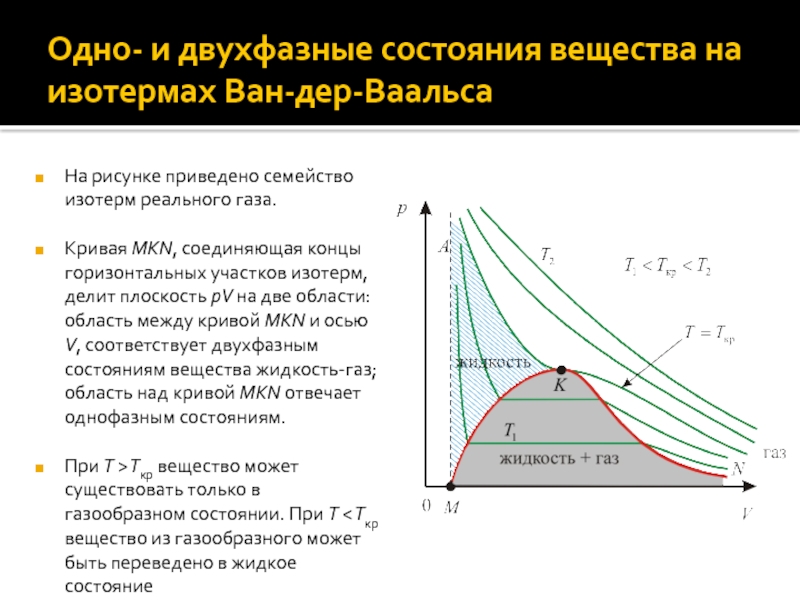
Слайд 20Одно- и двухфазные состояния вещества на изотермах Ван-дер-Ваальса
На рисунке приведено
семейство изотерм реального газа.
Кривая MKN, соединяющая концы горизонтальных участков изотерм,
делит плоскость pV на две области: область между кривой MKN и осью V, соответствует двухфазным состояниям вещества жидкость-газ; область над кривой MKN отвечает однофазным состояниям.
При T > Tкр вещество может существовать только в газообразном состоянии. При T < Tкр вещество из газообразного может быть переведено в жидкое состояние
Слайд 214.4 Критическое состояние вещества
ЛЕКЦИЯ 4. РЕАЛЬНЫЕ ГАЗЫ
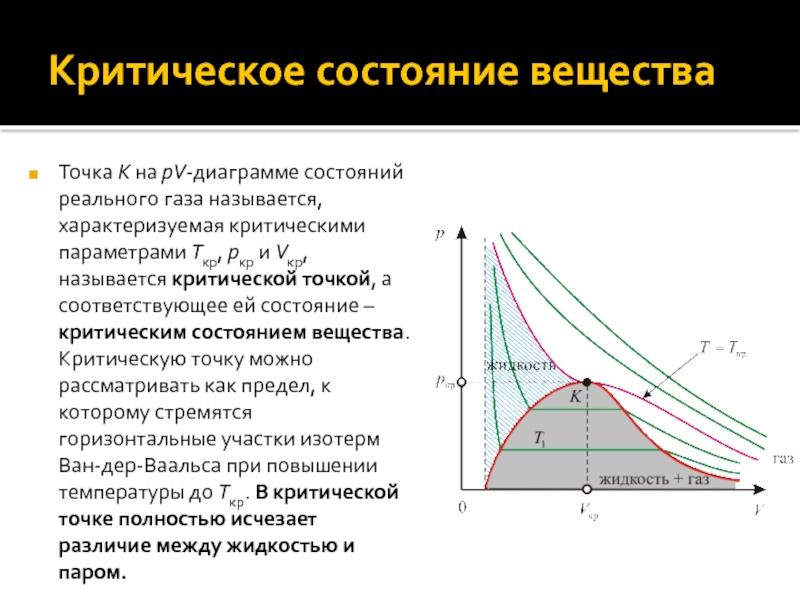
Слайд 22Критическое состояние вещества
Точка K на pV-диаграмме состояний реального газа называется,
характеризуемая критическими параметрами Tкр, pкр и Vкр, называется критической точкой,
а соответствующее ей состояние – критическим состоянием вещества. Критическую точку можно рассматривать как предел, к которому стремятся горизонтальные участки изотерм Ван-дер-Ваальса при повышении температуры до Tкр. В критической точке полностью исчезает различие между жидкостью и паром.
Слайд 23Плотность вещества
в критической точке
На рисунке представлена зависимость от температуры
T плотности насыщенного пара ρп и плотности жидкости ρж, находящейся
с ним в равновесии. При T = Tкр плотности становятся одинаковыми.
В критической точке сжимаемость вещества обращается в бесконечность:


































![Автоматизация звука
[ Р ] в слогах, словах, фразе,
предложениях, тексте у детей](/img/tmb/6/577954/93493577f437aaf90501124d2c9eb7d6-800x.jpg)