Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Регистры сдвига с обратными связями
Содержание
- 1. Регистры сдвига с обратными связями
- 2. КлассификацияРЕГИСТРЫПараллельныеРегистры сдвигаСпециальныеРегистры последовательных приближенийУниверсальные
- 3. Обратные связиСчетчик ДжонсонаУпорядоченная последовательностьУпорядоченная но очень сложная
- 4. Реализация обратных связейКонфигурация ФибоначчиКонфигурация ГалуаXORКоэффициент.Если gi=1 –
- 5. Последовательности максимальной длиныМ-последовательностиMaximum length sequenceЧисло состояний набора
- 6. Последовательности максимальной длиныКак сделать М-последовательностиРеализация вечностиФибоначчиилиГалуа
- 7. Последовательности максимальной длиныКак сделать М-последовательности. Кусок таблицы
- 8. Псевдослучайная последовательность. PRBS Pseudo Random Binary SequenceПоследовательность
- 9. Защита информацииQ=DataИдеяЗдесь полная мешанинаИсходные данныеВосстановленные данныеСлучайная последовательность
- 10. Защита информацииКлюч приемника должен совпадать с ключом приемника.Используется детерминированность ПСП.
- 11. Проверка целостности информацииКонтрольная сумма или циклический избыточный
- 12. Проверка целостности информацииДвоичная информацияЛюбая информация представляет собой
- 13. Контрольная суммаПредставление битовых последовательностей полиномами.1001101011=X9+X6+X5+X3+X1+1
- 14. Контрольная суммаПолиномиальная арифметика.Арифметика по модулю 2 (без переносов). XOR Суммирование = вычитаниюA=X9+X6+X5+X3+X1+1B=X6+X3+X2+1A+B=A-B=B-A= X9+X6+X5+X3+X1+1+ X6+X3+X2+1= X9+X5+X2+X1Переноса нет!
- 15. Контрольная суммаПолиномиальная арифметика.Арифметика по модулю 2A=X9+X6+X5+X3+X1+1B=X6+X3+X2+1УмножениеAxB=(X9+X6+X5+X3+X1+1)x(X6+X3+X2+1)=X15+X12+X11+X9+X7+X6+ X12+X9+X8+X6+X4+X3+ X12+X8+X7+X5+X3+X2+ X9+X6+X5+X3+X1+1 =X15+X12+X11+X9+X6+X4+X3+X2+X1+1
- 16. Контрольная суммаПолиномиальная арифметика.Арифметика по модулю 2A=X9+X6+X5+X3+X1+1B=X6+X3+X2+1ДелениеОстатокРезультат (целая часть)Это гораздо проще чем обычное деление.Разрядная сеткаУмножилиОтнялиУмножилиОтняли
- 17. Проверка целостности информацииПолучение остатка с помощью LFSRТакие
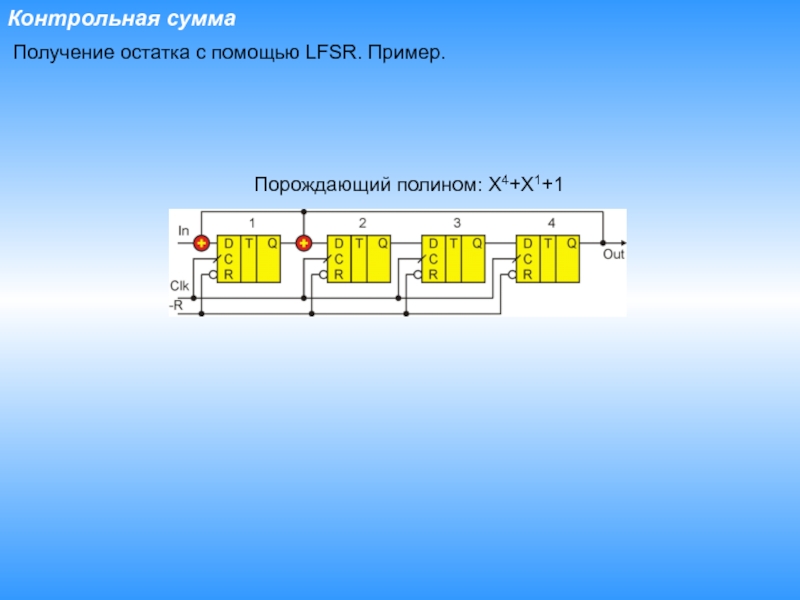
- 18. Контрольная суммаПорождающий полином: X4+X1+1Получение остатка с помощью LFSR. Пример.
- 19. Контрольная суммаПример. Кодирование.Порождающий полином: X4+X1+1ОстатокРезультат (целая часть).Ненужная
- 20. Контрольная суммаПример. Кодирование.Остаток X2Порождающий полином: X4+X1+1Старший разрядМладший разряд +1Разряд X1Разряд X2
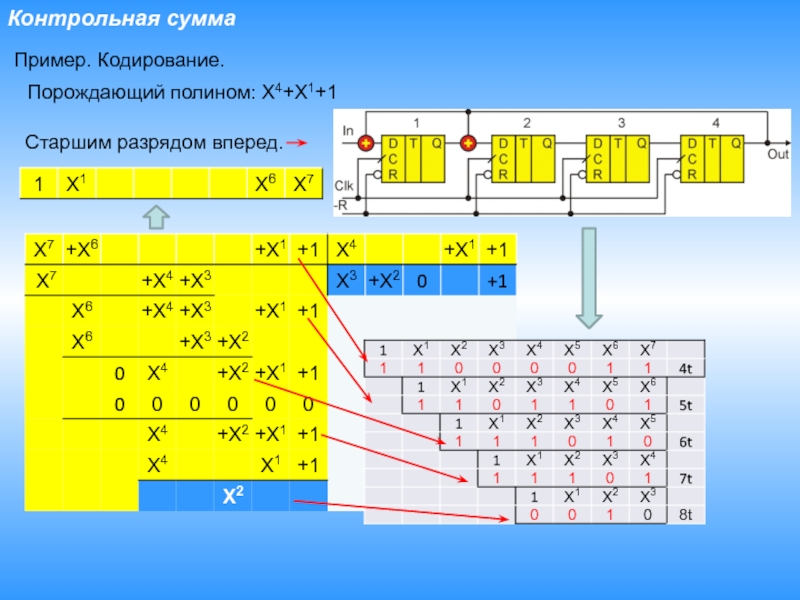
- 21. Контрольная суммаПример. Кодирование.Порождающий полином: X4+X1+1Старшим разрядом вперед.
- 22. CRCCyclic Redundancy Code
- 23. Контрольная сумма
- 24. СодержаниеОбратные связиКонфигурация ФибоначчиКонфигурация ГалуаМ-последовательностиПереход от номеров отводов
- 25. Скачать презентанцию
Слайды и текст этой презентации
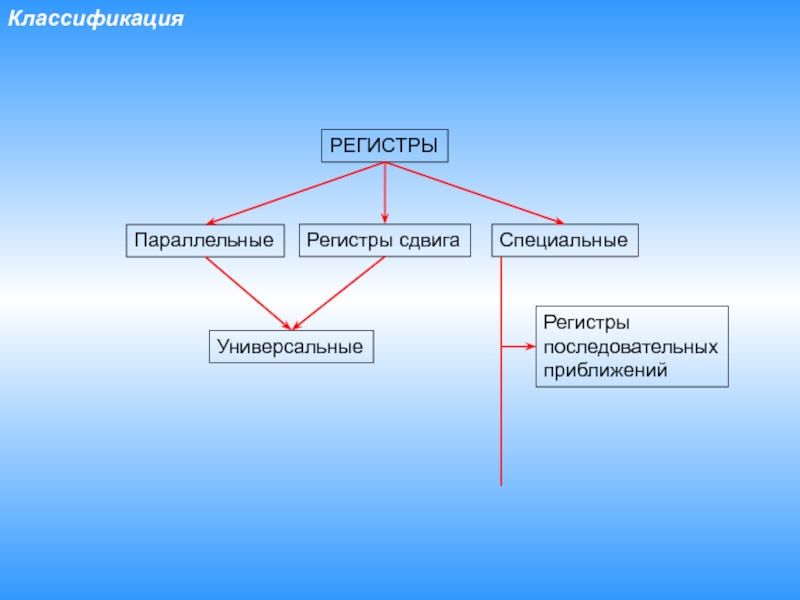
Слайд 2Классификация
РЕГИСТРЫ
Параллельные
Регистры сдвига
Специальные
Регистры последовательных приближений
Универсальные
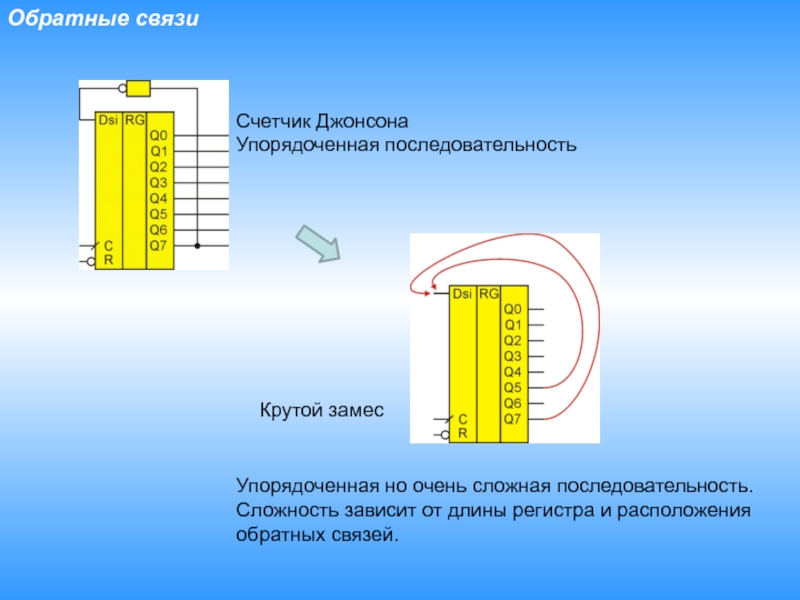
Слайд 3Обратные связи
Счетчик Джонсона
Упорядоченная последовательность
Упорядоченная но очень сложная последовательность.
Сложность зависит от
длины регистра и расположения обратных связей.
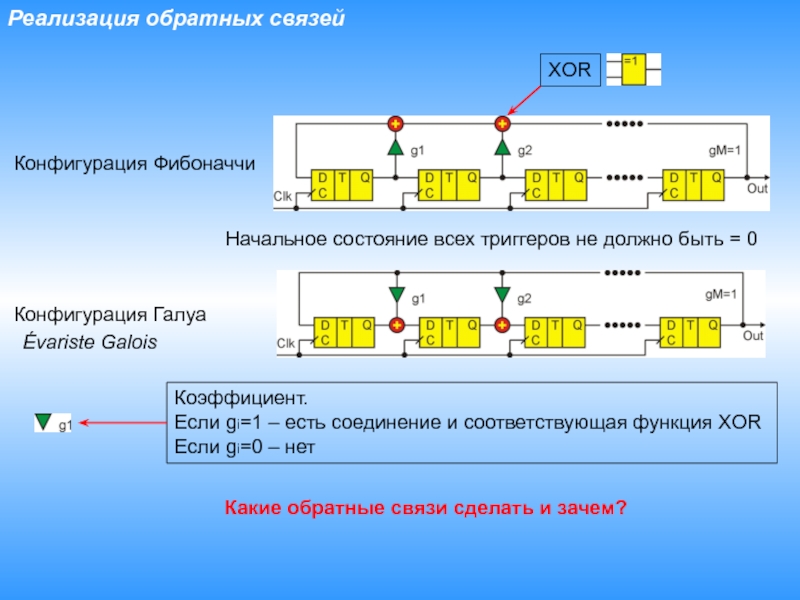
Слайд 4Реализация обратных связей
Конфигурация Фибоначчи
Конфигурация Галуа
XOR
Коэффициент.
Если gi=1 – есть соединение и
соответствующая функция XOR
Если gi=0 – нет
Какие обратные связи сделать и
зачем?Начальное состояние всех триггеров не должно быть = 0
Évariste Galois
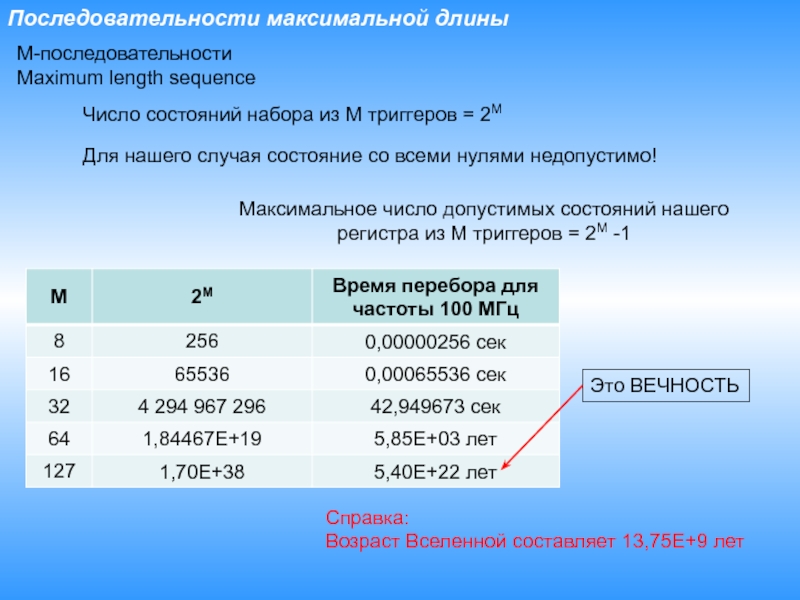
Слайд 5Последовательности максимальной длины
М-последовательности
Maximum length sequence
Число состояний набора из M триггеров
= 2M
Для нашего случая состояние со всеми нулями недопустимо!
Максимальное
число допустимых состояний нашего регистра из M триггеров = 2M -1Справка:
Возраст Вселенной составляет 13,75E+9 лет
Это ВЕЧНОСТЬ
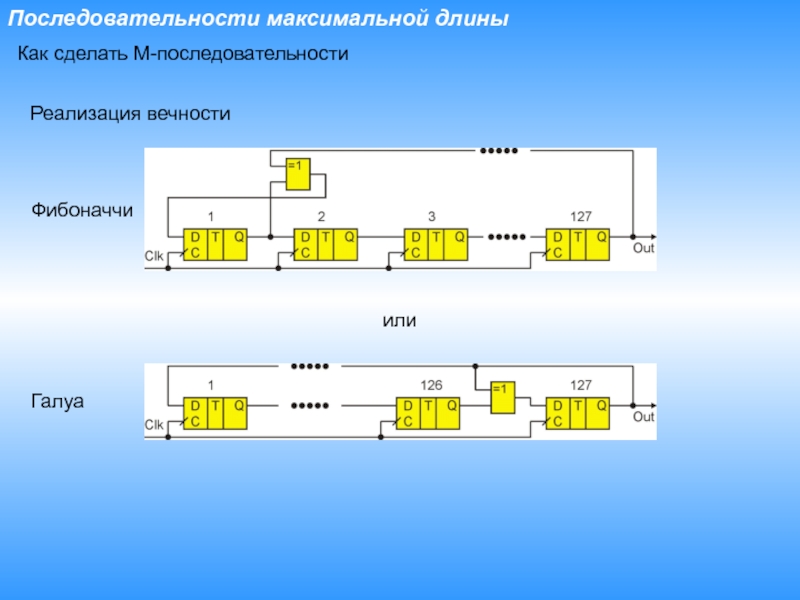
Слайд 6Последовательности максимальной длины
Как сделать М-последовательности
Реализация вечности
Фибоначчи
или
Галуа
Слайд 7Последовательности максимальной длины
Как сделать М-последовательности.
Кусок таблицы для конфигурации Галуа
Переход
от номеров отводов Галуа к Фибоначчи и наоборот:
M-g
(кроме
старшего).[20, 19, 16, 14]
[20, 1, 4, 6]
N- количество триггеров
Схема с 2-мя отводами
Схема с 4-мя отводами
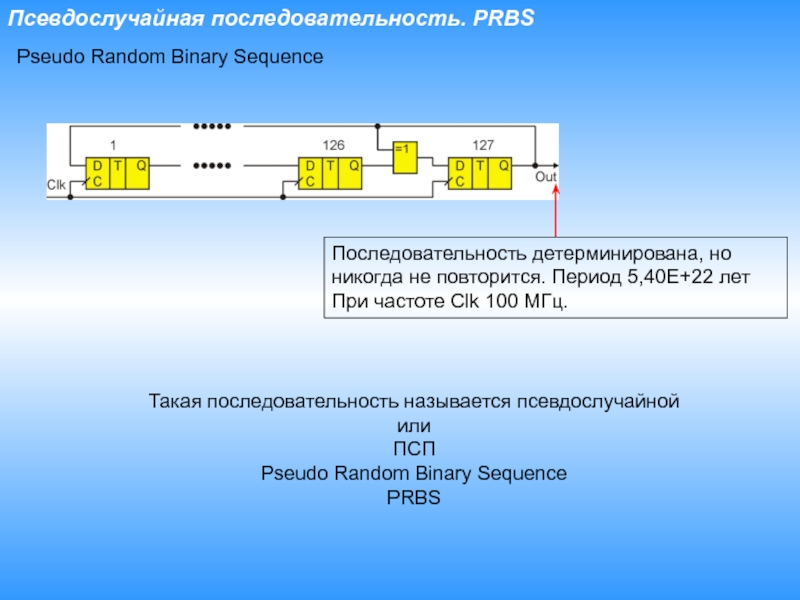
Слайд 8Псевдослучайная последовательность. PRBS
Pseudo Random Binary Sequence
Последовательность детерминирована, но никогда
не повторится. Период 5,40E+22 лет
При частоте Clk 100 МГц.
Такая последовательность
называется псевдослучайной илиПСП
Pseudo Random Binary Sequence
PRBS
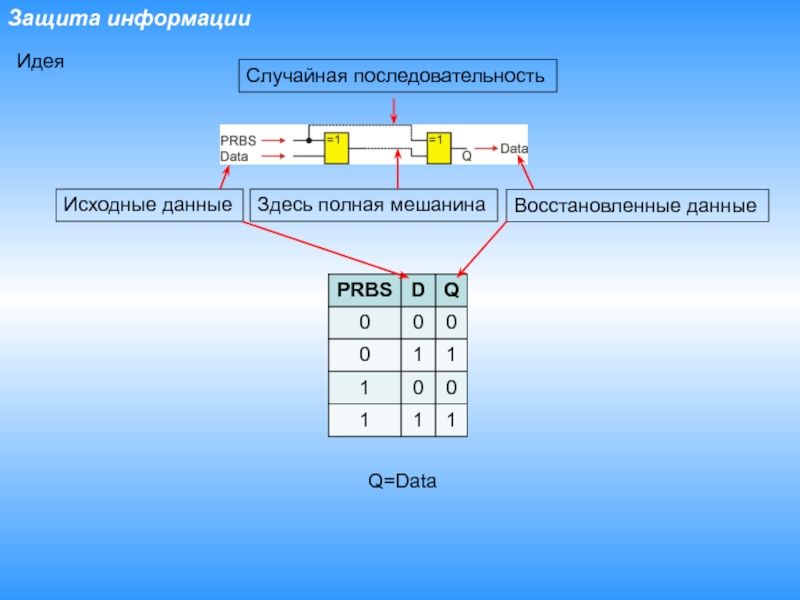
Слайд 9Защита информации
Q=Data
Идея
Здесь полная мешанина
Исходные данные
Восстановленные данные
Случайная последовательность
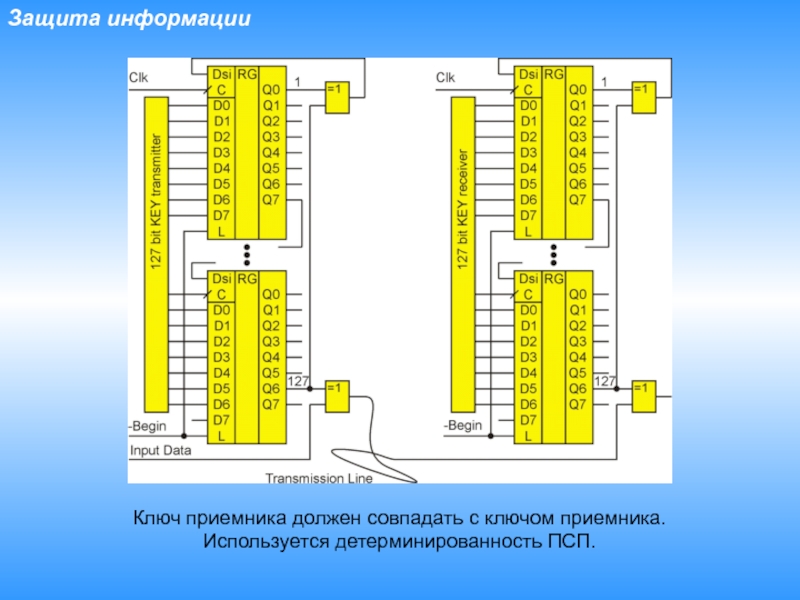
Слайд 10Защита информации
Ключ приемника должен совпадать с ключом приемника.
Используется детерминированность ПСП.
Слайд 11Проверка целостности информации
Контрольная сумма или циклический избыточный код
Cyclic Redundancy
Code (CRC)
ИДЕЯ МЕТОДА
Допустим надо передать (или сохранить) десятичное число 23567.
Возможно искажение. Как проверить правильность числа?
Поделить исходное число на какую либо постоянную. Допустим на 23. В результате целочисленного деления получим 1024 и остаток 15. Если теперь к исходному числу прибавить 15, то новое число будет делиться на 23 без остатка. Это признак правильности. Но исходное число будет потеряно.
Выход. Число 23567 дополняем нулями. Количество нулей должно совпадать с разрядностью остатка (делителя). Получаем 2356700. Теперь это число делим на 23. Получаем 102465 и остаток 05. Интересует только остаток. Храним или передаем число в форме 2356705.
Исходные данные
Контрольная сумма
При приеме делим 2356705 на наше 23.
Если остаток ≠ 0, то число искажено.
Если остаток = 0, то число с некоторой вероятностью правильное.
Слайд 12Проверка целостности информации
Двоичная информация
Любая информация представляет собой набор 0 и
1.
10010001011110001010100100100101010010001111010
В соответствии с идеей надо дописать слово нулями
100100010111100010101001001001010100100011110100000
взять некий
делитель, например 1011(с разрядностью по количеству дописанных нулей.Поделить
Дописать вместо нулей остаток от деления.
10010001011110001010100100100101010010001111010xxxx
Хранить или передавать в такой форме.
Перед использование проверить на делимость без остатка на 1011.
Все по идее просто, но
Делить – это долго и муторно!!!
Даже для этого примера лень было найти реальный остаток и написал xxxx
Нужна другая БЫСТРАЯ арифметика.
Слайд 13Контрольная сумма
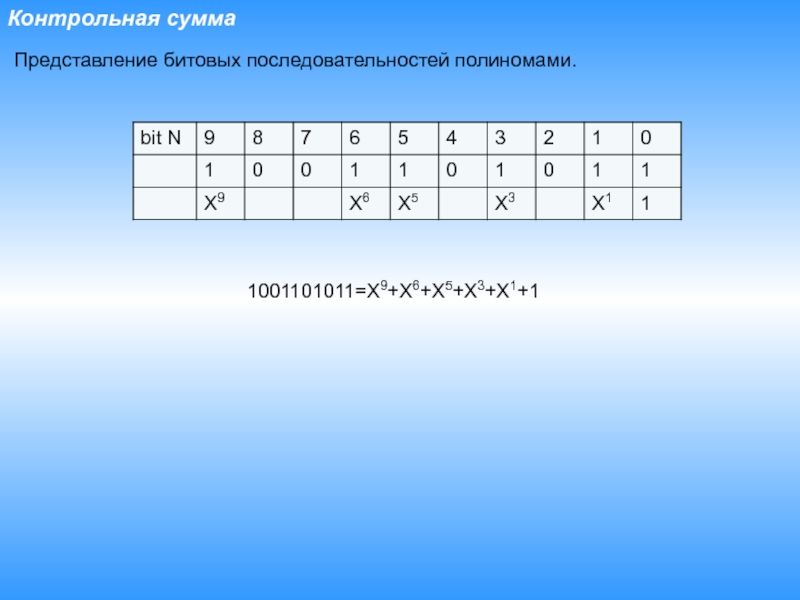
Представление битовых последовательностей полиномами.
1001101011=X9+X6+X5+X3+X1+1
Слайд 14Контрольная сумма
Полиномиальная арифметика.
Арифметика по модулю 2 (без переносов).
XOR
Суммирование = вычитанию
A=X9+X6+X5+X3+X1+1
B=X6+X3+X2+1
A+B=A-B=B-A=
X9+X6+X5+X3+X1+1+ X6+X3+X2+1= X9+X5+X2+X1
Переноса нет!
Слайд 15Контрольная сумма
Полиномиальная арифметика.
Арифметика по модулю 2
A=X9+X6+X5+X3+X1+1
B=X6+X3+X2+1
Умножение
AxB=(X9+X6+X5+X3+X1+1)x(X6+X3+X2+1)=
X15+X12+X11+X9+X7+X6+ X12+X9+X8+X6+X4+X3+ X12+X8+X7+X5+X3+X2+ X9+X6+X5+X3+X1+1 =
X15+X12+X11+X9+X6+X4+X3+X2+X1+1
Слайд 16Контрольная сумма
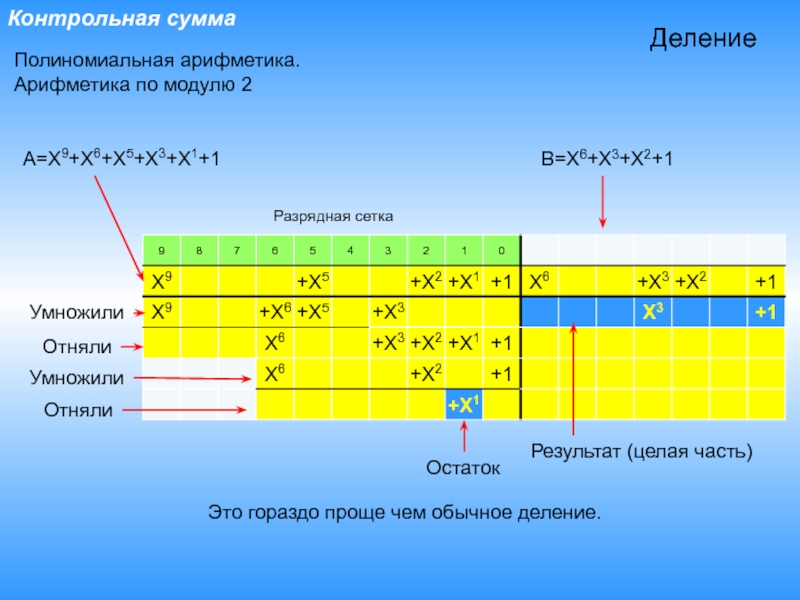
Полиномиальная арифметика.
Арифметика по модулю 2
A=X9+X6+X5+X3+X1+1
B=X6+X3+X2+1
Деление
Остаток
Результат (целая часть)
Это гораздо проще
чем обычное деление.
Разрядная сетка
Умножили
Отняли
Умножили
Отняли
Слайд 17Проверка целостности информации
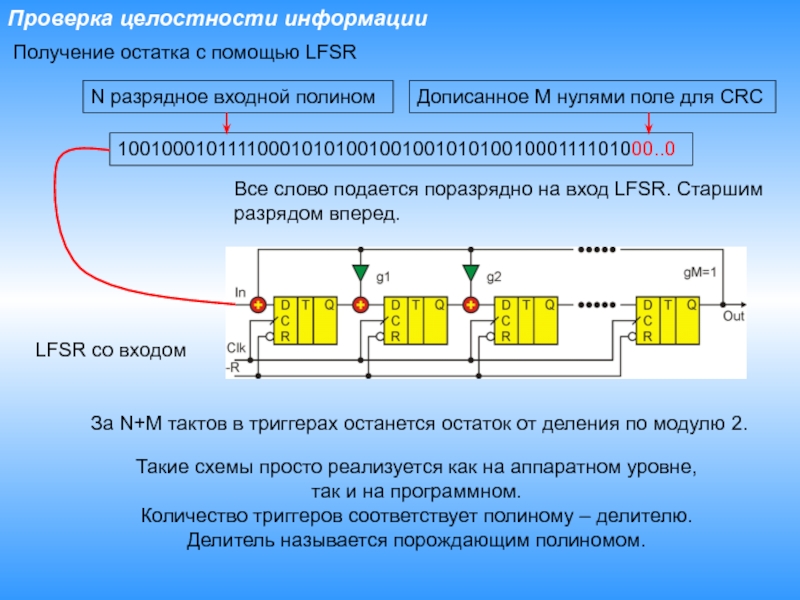
Получение остатка с помощью LFSR
Такие схемы просто реализуется
как на аппаратном уровне, так и на программном.
Количество триггеров соответствует
полиному – делителю.Делитель называется порождающим полиномом.
LFSR со входом
1001000101111000101010010010010101001000111101000..0
N разрядное входной полином
Дописанное M нулями поле для CRC
Все слово подается поразрядно на вход LFSR. Старшим разрядом вперед.
За N+M тактов в триггерах останется остаток от деления по модулю 2.
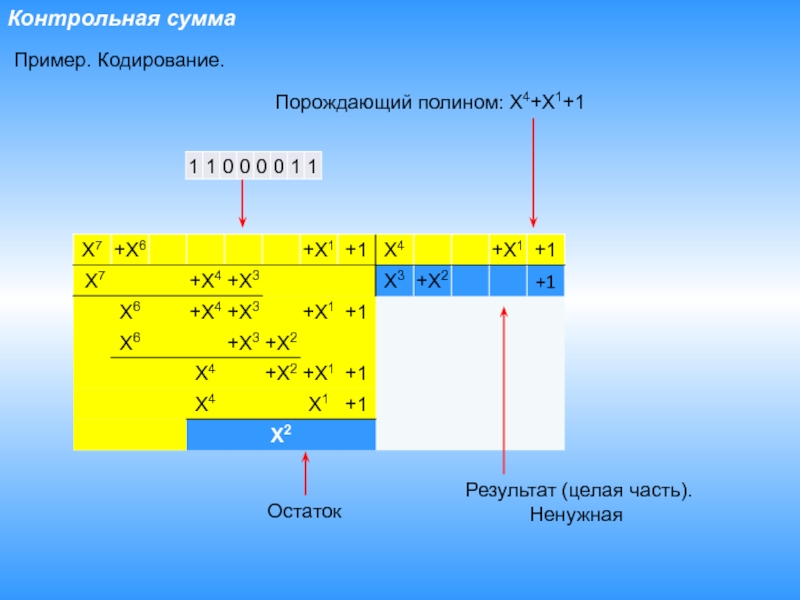
Слайд 19Контрольная сумма
Пример. Кодирование.
Порождающий полином: X4+X1+1
Остаток
Результат (целая часть).
Ненужная
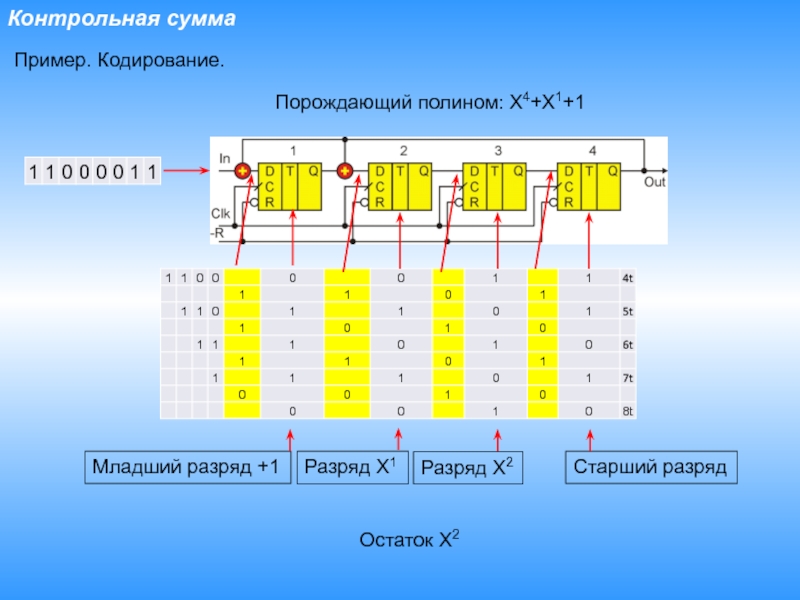
Слайд 20Контрольная сумма
Пример. Кодирование.
Остаток X2
Порождающий полином: X4+X1+1
Старший разряд
Младший разряд +1
Разряд X1
Разряд
Слайд 24Содержание
Обратные связи
Конфигурация Фибоначчи
Конфигурация Галуа
М-последовательности
Переход от номеров отводов Галуа к Фибоначчи
и наоборот
Pseudo Random Binary Sequence
Защита информации
Ключ приемника должен совпадать с
ключом приемникаКонтрольная сумма или циклический избыточный код
Идея метода
Представление битовых последовательностей полиномами
Полиномиальная арифметика -арифметика по модулю 2 (без переносов)
Сложение = вычитание
Умножение
Деление
Получение остатка с помощью LFSR
Получение остатка с помощью LFSR. Пример.
Примеры CRC. E1, RFID, SD, 1-Wire, Bluetooth, Ethernet, Wi-Fi …