Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
РЕЛЯЦИОННАЯ МОДЕЛЬ ДАННЫХ
Содержание
- 1. РЕЛЯЦИОННАЯ МОДЕЛЬ ДАННЫХ
- 2. Реляционная модель (relational model) Реляционная модель данных
- 3. Реляционная модель (relational model)
- 4. Операции реляционной алгебрыБазовые теоретико-множественные операции объединение, разность, пересечение,декартово произведение.Специальные реляционные операции: проекция,выборка, деление, соединение.
- 5. ОбъединениеОбъединением двух совместимых отношений R1 и R2
- 6. ВычитаниеРазностью двух совместимых отношений R1 и R2
- 7. ПересечениеПересечение двух совместимых отношений R1 и R2
- 8. Декартово произведениеПроизведение отношения R1 степени k1 и
- 9. ВыборкаВыборка (R Where f) отношения R по
- 10. ПроекцияПроекция отношения R на атрибуты X, Y,
- 11. ДелениеРезультатом деления отношения R1 с атрибутами A
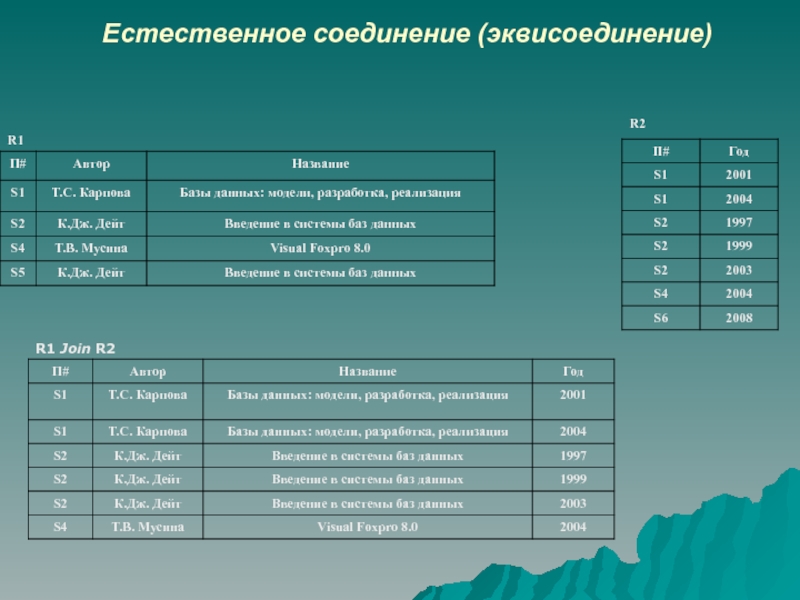
- 12. Естественное соединение (эквисоединение)Пусть отношения R1 и R2
- 13. Естественное соединение (эквисоединение)
- 14. Скачать презентанцию
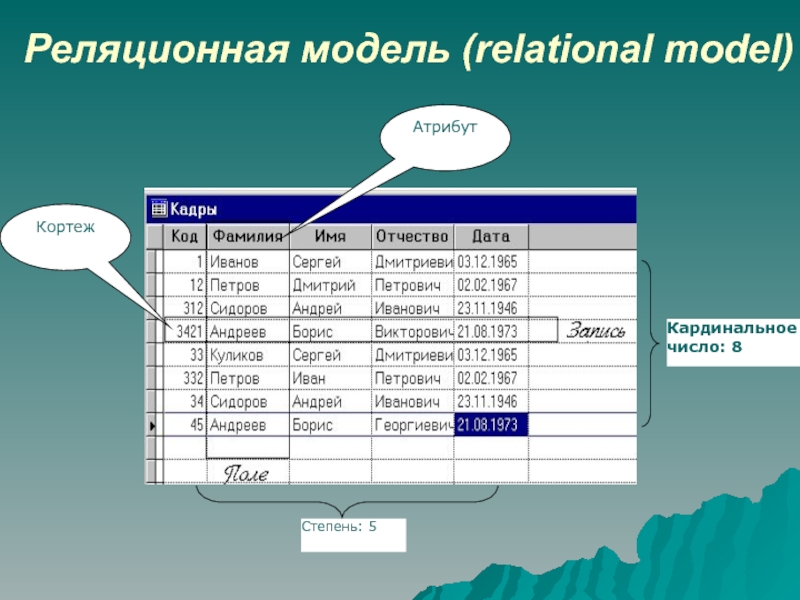
Реляционная модель (relational model) Реляционная модель данных некоторой предметной области представляет собой набор отношений, изменяющихся во времени. В отношении (таблице) реляционной модели все атрибуты являются простыми (имеют единственное значение, на пересечении каждого
Слайды и текст этой презентации
Слайд 2Реляционная модель (relational model)
Реляционная модель данных некоторой предметной области
представляет собой набор отношений, изменяющихся во времени.
модели все атрибуты являются простыми (имеют единственное значение, на пересечении каждого столбца и каждой строки находятся только элементарные значения атрибутов).Слайд 4Операции реляционной алгебры
Базовые теоретико-множественные операции
объединение,
разность,
пересечение,
декартово произведение.
Специальные реляционные
операции:
проекция,
выборка,
деление,
соединение.
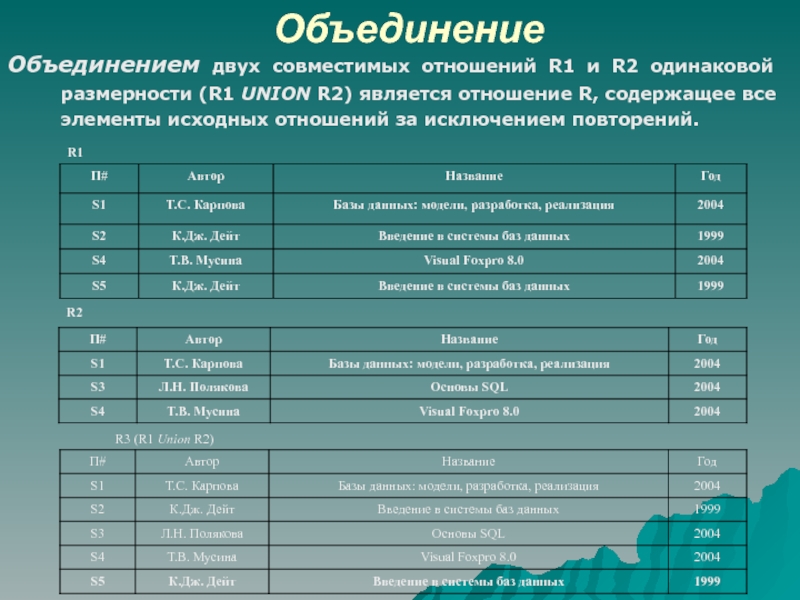
Слайд 5Объединение
Объединением двух совместимых отношений R1 и R2 одинаковой размерности (R1
UNION R2) является отношение R, содержащее все элементы исходных отношений
за исключением повторений.Слайд 6Вычитание
Разностью двух совместимых отношений R1 и R2 одинаковой размерности (R1
Minus R2) является отношение, тело которого состоит из множества кортежей,
принадлежащих R1, но не принадлежащих R2.Слайд 7Пересечение
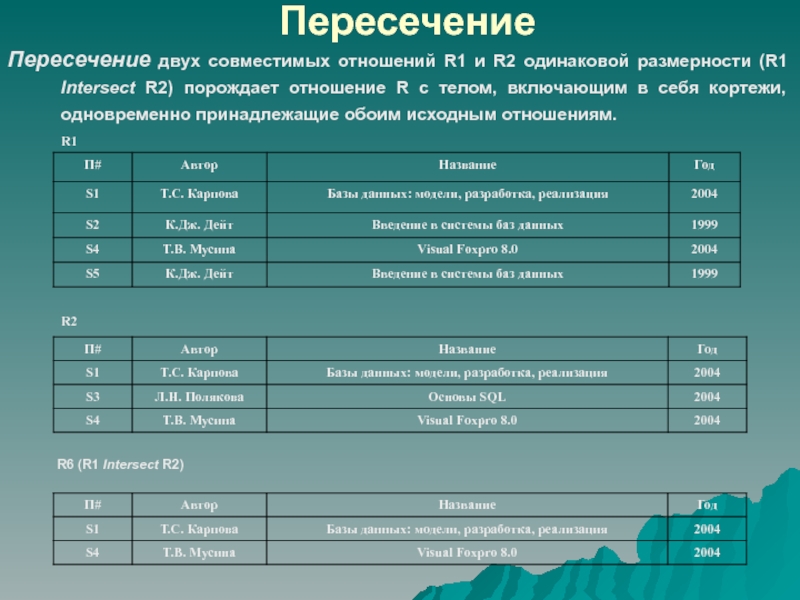
Пересечение двух совместимых отношений R1 и R2 одинаковой размерности (R1
Intersect R2) порождает отношение R с телом, включающим в себя
кортежи, одновременно принадлежащие обоим исходным отношениям.R6 (R1 Intersect R2)
Слайд 8Декартово произведение
Произведение отношения R1 степени k1 и отношения R2 степени
k2 (R1 Times R2), которые не имеют одинаковых имен атрибутов,
есть такое отношение R степени (k1+k2), заголовок которого представляет сцепление заголовков отношений R1 и R2, а тело – имеет кортежи, такие, что первые k1 элементов кортежей принадлежат множеству R1, а последние k2 элементов множеству – R2. Кардинальное число результата равняется произведению кардинальных чисел исходных отношений R1 и R2.Слайд 9Выборка
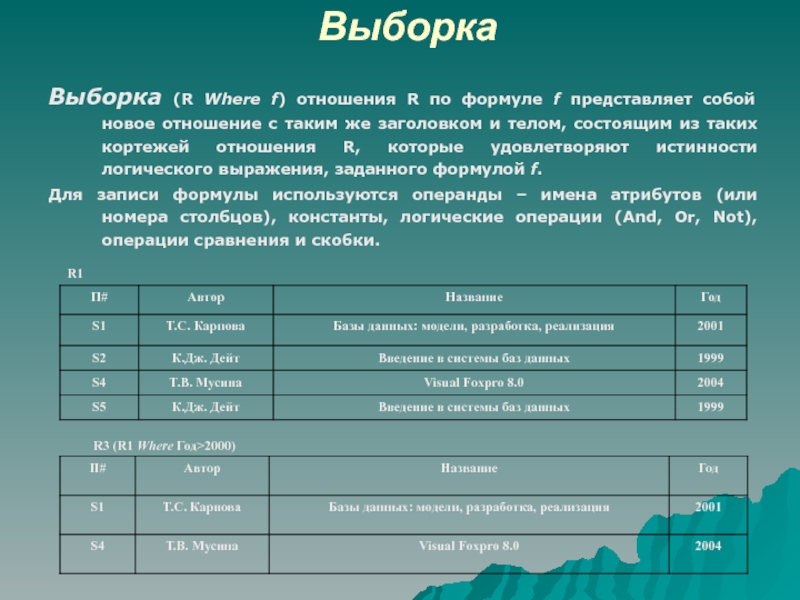
Выборка (R Where f) отношения R по формуле f представляет
собой новое отношение с таким же заголовком и телом, состоящим
из таких кортежей отношения R, которые удовлетворяют истинности логического выражения, заданного формулой f.Для записи формулы используются операнды – имена атрибутов (или номера столбцов), константы, логические операции (And, Or, Not), операции сравнения и скобки.
Слайд 10Проекция
Проекция отношения R на атрибуты X, Y, …, Z (R[X,
Y, …, Z]). Где множество {X, Y, …, Z} является
подмножеством полного списка атрибутов заголовка отношения R, представляет собой отношение с заголовком X, Y, …, Z и телом, содержащим кортежи отношения R, за исключением повторяющихся кортежей. Повторение одинаковых атрибутов в списке X, Y, …, Z запрещается.Слайд 11Деление
Результатом деления отношения R1 с атрибутами A и B на
отношение R2 с атрибутом B (R1 Divideby R2), где атрибут
B – общий атрибут, определенный на одном и том же домене, является отношение R с заголовком A и телом, состоящим из кортежей r таких, что в отношении R1 имеются кортежи (r, s), причем множество значений s включает множество значений атрибута B отношения R2.Слайд 12Естественное соединение (эквисоединение)
Пусть отношения R1 и R2 имеют заголовки
{X1, X2,
…, Xm, Y1, Y2, …, Yn}
и
{Y1, Y2, …, Yn, Z1,
Z2, …, Zk}соответственно. Предположим, что атрибуты с одинаковыми именами определены на одном и том же домене. Будем рассматривать выражения {X1, X2, …, Xm}, {Y1, Y2, …, Yn} и {Z1, Z2, …, Zk} как три составных атрибута X, Y и Z соответственно.
Тогда естественным соединением отношений R1 и R2 (R1 Join R2) называется отношение с заголовком {X, Y, Z} и телом, содержащим множество всех кортежей {X:x, Y:y, Z:z}, таких, для которых в отношении R1 значение атрибута X равно x, а атрибута Y равно y, и в отношении R2 значение атрибута Y равно y, а атрибута Z равно z.





![РЕЛЯЦИОННАЯ МОДЕЛЬ ДАННЫХ ПроекцияПроекция отношения R на атрибуты X, Y, …, Z (R[X, Y, ПроекцияПроекция отношения R на атрибуты X, Y, …, Z (R[X, Y, …, Z]). Где множество {X, Y,](/img/thumbs/eab169bdd02632be68f39fb83613c6c6-800x.jpg)