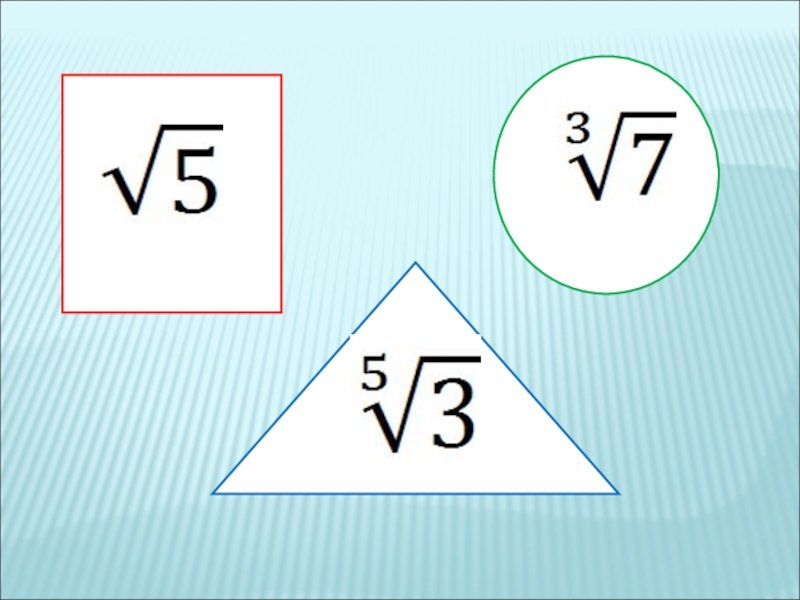
Решение иррациональных уравнений 11 класс

Содержание

1. Решение иррациональных уравнений 11 класс
2. Цель урока: Обобщить и закрепить методы решения
3. « Мне приходится делить свое время между
4. Слайд 4
5. Разминка
6. Как называется знак корня?
7. Сколько решений имеет уравнение х2 = а, если а 0 ?
8. Как называются уравнения, в которых под знаком корня содержится переменная?
9. Как называется корень второй степени?
10. Сколько решений имеет уравнение х2 = 0?
11. Корень какой степени существует из любого числа?
12. Как называется равенство двух алгебраических выражений?
13. Корень какой степени существует только из неотрицательного числа?
14. Из предложенных уравнений назовите номера тех, которые являются иррациональными 1. 2.3.4.5.6.7.8.
15. Метод мажорантМажоранта и миноранта – (от франц.)
16. Решим уравнение: - 6х + 11Решение:ОДЗ: 1.
17. В результате f(x) 2
18. Закончить предложения: Я
19. Докажите, что уравнение не имеет корней 1. 2.3.4.
20. Решите уравнение:1.2.3. = 74.
21. Решите уравнениеРешение:В ответ запишите корень уравнения или
22. Скачать презентанцию

Цель урока: Обобщить и закрепить методы решения иррациональных уравнений; Познакомить с новым нестандартным методом решения иррациональных уравнений – методом мажорант

Главная
Разное
Решение иррациональных уравнений 11 класс

Слайды и текст этой презентации

Слайд 1Решение
иррациональных
уравнений
Учитель: Иванова ТВ

Слайд 2Цель урока:
Обобщить и закрепить методы решения
иррациональных уравнений;

Познакомить с новым нестандартным методом
решения иррациональных

уравнений – методом мажорант

Цель урока: Обобщить и закрепить методы решения иррациональных уравнений; Познакомить с новым нестандартным методом

Слайд 3« Мне приходится делить свое время между политикой и уравнениями.

Однако уравнения, по-моему, гораздо важнее, потому что политика существует только

для данного момента, а уравнения будут существовать вечно.»

А. Эйнштейн

« Мне приходится делить свое время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее, потому что

Слайд 4

Слайд 5Разминка

Слайд 6Как называется знак корня?

Слайд 7Сколько решений имеет
уравнение х2 = а,
если а

0 ?

Сколько решений имеет уравнение х2 = а, если а 0 ?

Слайд 8Как называются уравнения,
в которых под знаком корня
содержится переменная?

Слайд 9Как называется корень
второй степени?

Слайд 10Сколько решений имеет
уравнение х2 = 0?

Слайд 11Корень какой степени существует
из

любого числа?

Слайд 12Как называется равенство
двух алгебраических

выражений?

Слайд 13Корень какой степени существует
только из неотрицательного числа?

Слайд 14Из предложенных уравнений назовите номера тех, которые являются иррациональными

1.

2.

3.

4.

5.

6.

7.

8.

Слайд 15Метод мажорант
Мажоранта и миноранта – (от франц.) две функции, значение

первой
из которой не меньше, а второй не больше соответствующих

значений
данной функции.

Мажорирование – нахождение точек ограничения функции.

Метод мажорант – метод оценки левой и правой части уравнения.

М – мажоранта.

Если f(x) = g(x) и f(x) М g(x) М, то М = f(x) и М = g(x)

Метод мажорантМажоранта и миноранта – (от франц.) две функции, значение первой из которой не меньше, а второй

Слайд 16Решим уравнение:

- 6х + 11
Решение:
ОДЗ:

1. Рассмотрим правую часть

уравнения. Введем функцию g(x) = - 6х + 11

Графиком функции является парабола с вершиной А(3; 2).
Следовательно наименьшее значение функции g(3) = 2
2. Рассмотрим левую часть уравнения . Введем функцию
f(x) =
C помощью производной найдем max функции, которая дифференцируема на (2;4)

(х) = - = ОДЗ: 2 х 4

(х) = 0, если = 0; ; х = 3

+ -
(3) = 2 И так М = 2
2 3 4

Решим уравнение: - 6х + 11Решение:ОДЗ: 1. Рассмотрим правую часть уравнения. Введем функцию g(x) = -

Слайд 17В результате f(x) 2 и

g(x) 2 , отсюда f(x) = 2

и g(x) = 2
Из этих условий составим систему уравнений
х2 - 6х + 11= 2 и = 2
Решением этой системы х = 3

Ответ: х = 3

Метод мажорант:

Оценим левую часть уравнения
Оценим правую часть уравнения
Составим систему уравнений
Сделаем вывод
Проверка