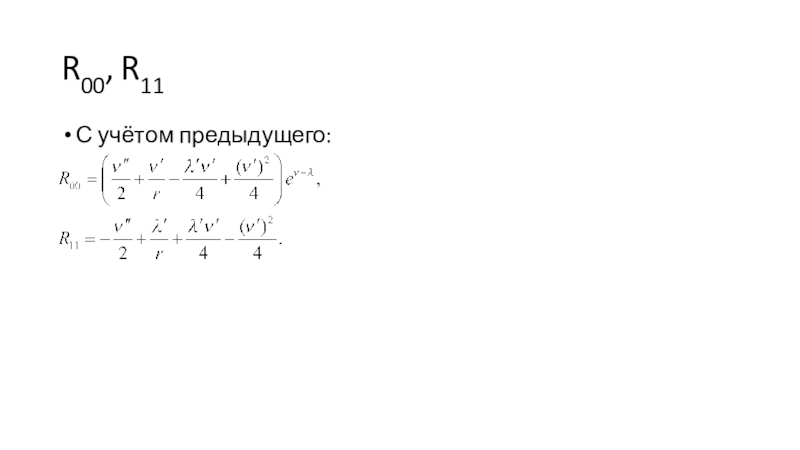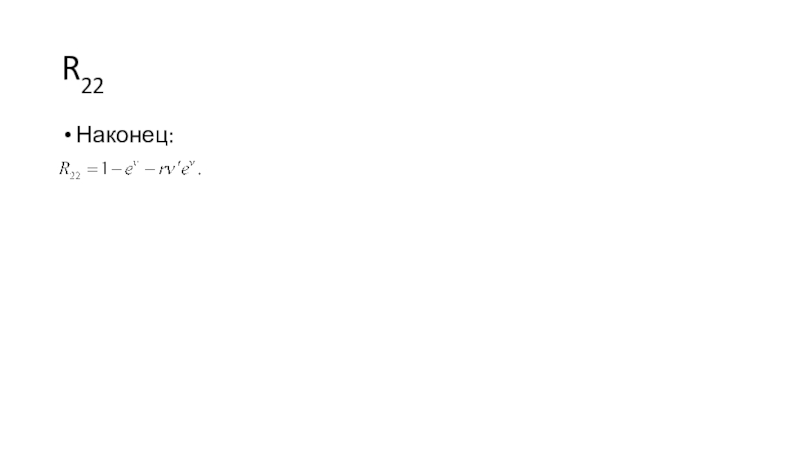Разделы презентаций
- Разное
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Решение Шварцшильда
Содержание
- 1. Решение Шварцшильда
- 2. Центрально-симметричное полеОбщий вид квадрата интервалаВозможно преобразование координат,
- 3. Символы Кристоффеля (0)Последовательно и методично вычисляем:
- 4. Символы Кристоффеля (1)Последовательно и методично вычисляем:
- 5. Символы Кристоффеля (2)Последовательно и методично вычисляем:
- 6. Символы Кристоффеля (3)Последовательно и методично вычисляем:
- 7. Тензор РиччиС ним всё плохо, но ненулевые – только 6 компонент:
- 8. R01Можно упростить вычисления, если удачно выбрать их порядок:
- 9. R01Получается:
- 10. R00, R11С учётом предыдущего:
- 11. R22Наконец:
- 12. Метрика ШварцшильдаПосле всех ужасов:
- 13. Гравитационное замедление времениС точки зрения удалённого наблюдателя, для тел вблизи rg время идёт медленнее:
- 14. Ускорение материальной точкиУравнение движения: Если в некоторой СК тело покоится, то:
- 15. Радиальное падение на горизонт событийУравнение движения: Работаем с i = 0
- 16. Радиальное падение на горизонт событийВремя падения (смотрим издали):Время падения (падаем сами):
- 17. Орбиты в поле ШварцшильдаУравнение Гамильтона – Якоби:
- 18. Орбиты в поле ШварцшильдаИспользуем общие приёмы из теор.механики: Параметрические уравнения орбиты:
- 19. Орбиты в поле ШварцшильдаУстойчивость орбит:
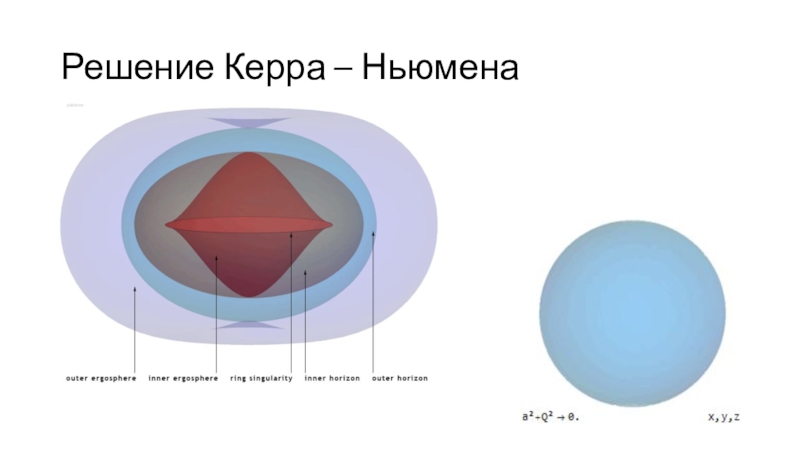
- 20. Решение Керра – НьюменаАксиально-симметричная задача:
- 21. Решение Керра – Ньюмена
- 22. Скачать презентанцию
Центрально-симметричное полеОбщий вид квадрата интервалаВозможно преобразование координат, приводящее к В пределе слабого поля (вдали от центра) должно быть Можно ввести экспоненциальные функции:
Слайды и текст этой презентации
Слайд 2Центрально-симметричное поле
Общий вид квадрата интервала
Возможно преобразование координат,
приводящее к
В
пределе слабого поля (вдали от центра) должно быть
экспоненциальные функции:
Слайд 13Гравитационное замедление времени
С точки зрения удалённого наблюдателя,
для тел вблизи rg
время идёт медленнее:
Слайд 16Радиальное падение на горизонт событий
Время падения (смотрим издали):
Время падения (падаем
сами):
Слайд 18Орбиты в поле Шварцшильда
Используем общие приёмы из теор.механики:
Параметрические уравнения орбиты:
